尾流激励的叶片气动力降阶模型
, , , ,
(1.中北大学 机电工程学院,太原 030051;2.太原学院 数学系,太原 030001)
1 引 言
航空发动机中存在气流导向的静叶和对外做功的动叶。当动静叶相对转动时,上游叶片的尾流会使下游叶片的气动力产生周期性振荡[1,2],迫使下游叶片强迫振动,如图1所示。这是导致航空发动机叶片疲劳破坏的重要原因。近年来的一些研究发现,周期变化的尾流甚至可以改变动叶的颤振特性[3-7]。因此,研究上游尾流激励下叶片的气动弹性振动对航空发动机的设计有十分重要的意义。

图1 上游尾流激励的叶片
Fig.1 Blade under incoming wake
计算流体力学(CFD)和计算结构力学(CSM)耦合的求解方法是研究叶片气动弹性振动的主要方法,但其计算效率极低,对计算设备要求很高,很难在日常工程研究中应用[8-11]。建立叶片气动弹性振动精确高效的研究方法已成为航空发动机设计中亟待解决的问题。
气动力降阶模型(aerodynamic ROM)是描述叶片气动力和扰动之间相互关系的简化数学模型。其通过模型辨识,从已知的气动试验数据或仿真数据中识别降阶模型的主要参数,建立扰动和气动力之间的函数关系。气动力降阶模型的数学形式简单,在气动弹性振动时不需要进行整个流场的气动重分析,所以计算量小、计算速度快,广泛应用于叶片颤振边界的预测[8-17]。Silva[8]提出了基于Volterra级数的非线性气动力降阶模型。张伟伟等[12-14,16]基于Volterra级数降阶模型研究了叶栅的颤振性能。Ekici等[15]用谐波平衡方法研究了叶片颤振,认为该方法的结果与势流理论的结果符合较好。
现有气动力降阶模型的研究主要集中在叶片颤振方面,没有涉及更为常见的上游尾流激励的叶片气动弹性振动问题。本文建立了基于Volterra级数的尾流激励的叶片气动力降阶模型,并通过二维叶片的算例验证该降阶模型方法的可行性。
2 尾流激励的叶片气动力降阶模型
Volterra级数可以用来描述任意复杂时变系统输入和输出之间的关系。对于均匀采样的线性时变系统Ψ,可以用一阶离散格式的Volterra级数表示为[8]

(1)
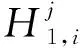
Volterra级数模型中的核函数可以用原系统的输入输出数据加以辨识,辨识方法包括脉冲信号法、阶跃信号法以及白噪声信号法等[8,12-15,16-18]。对核函数辨识的具体方法可参考系统辨识相关理论[18]。
叶片气动力系统是一个弱非线性系统,可以用一个定常的非线性解和若干个非定常线性解的叠加表示。为此,可以用一阶Volterra级数降阶模型表示尾流激励和叶片气动力之间的相互关系。
本文建立基于一阶Volterra级数的尾流激励叶片气动力降阶模型。为方便介绍,以二维叶片为例说明本文方法。尾流激励的叶片流场系统如图2所示。上游叶片以速度w沿着y向移动,上游尾流的移动导致下游叶片气动力的周期性振荡。在这一气动力系统中,输入为时变尾流的进口总压p和进气角β,输出为叶片气动力,包括升力CL、力矩CM和阻力CD,如图2所示。为简化问题,本文只考虑升力和力矩,则该系统可以表示为
{CL(t),CM(t)}=Ψ{p(y,t),β(y,t)}
(2)
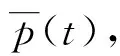
(3)
将式(3)按照一阶离散格式的Volterra级数展开,得到尾流激励的叶片气动力降阶模型为

图2 尾流激励的叶片气动力系统
Fig.2 Blade aerodynamic system under wake excitation
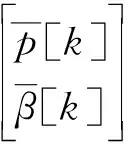
(4)
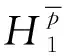
3 尾流激励叶片的算例
按照前述方法,建立图1下游叶片的气动力降阶模型。稳态进口总压120.5 kPa,稳态进气角30°,尾流以10 m/s的速度沿着进口y向移动。取下游中间叶片的气动升力和力矩为输出,下游进口最下方点的总压和进气角为输入。用流场CFD模型分别计算总压和进气角阶跃信号下,中间叶片的气动升力和力矩,用阶跃信号法辨识降阶模型的核函数。总压的阶跃信号为1 kPa,进气角的阶跃信号为3°。核函数的辨识结果如图3所示。将辨识得到的核函数代入式(4),得到尾流激励的叶片气动力降阶模型,可以用来预测任意尾流激励下叶片气动力响应。

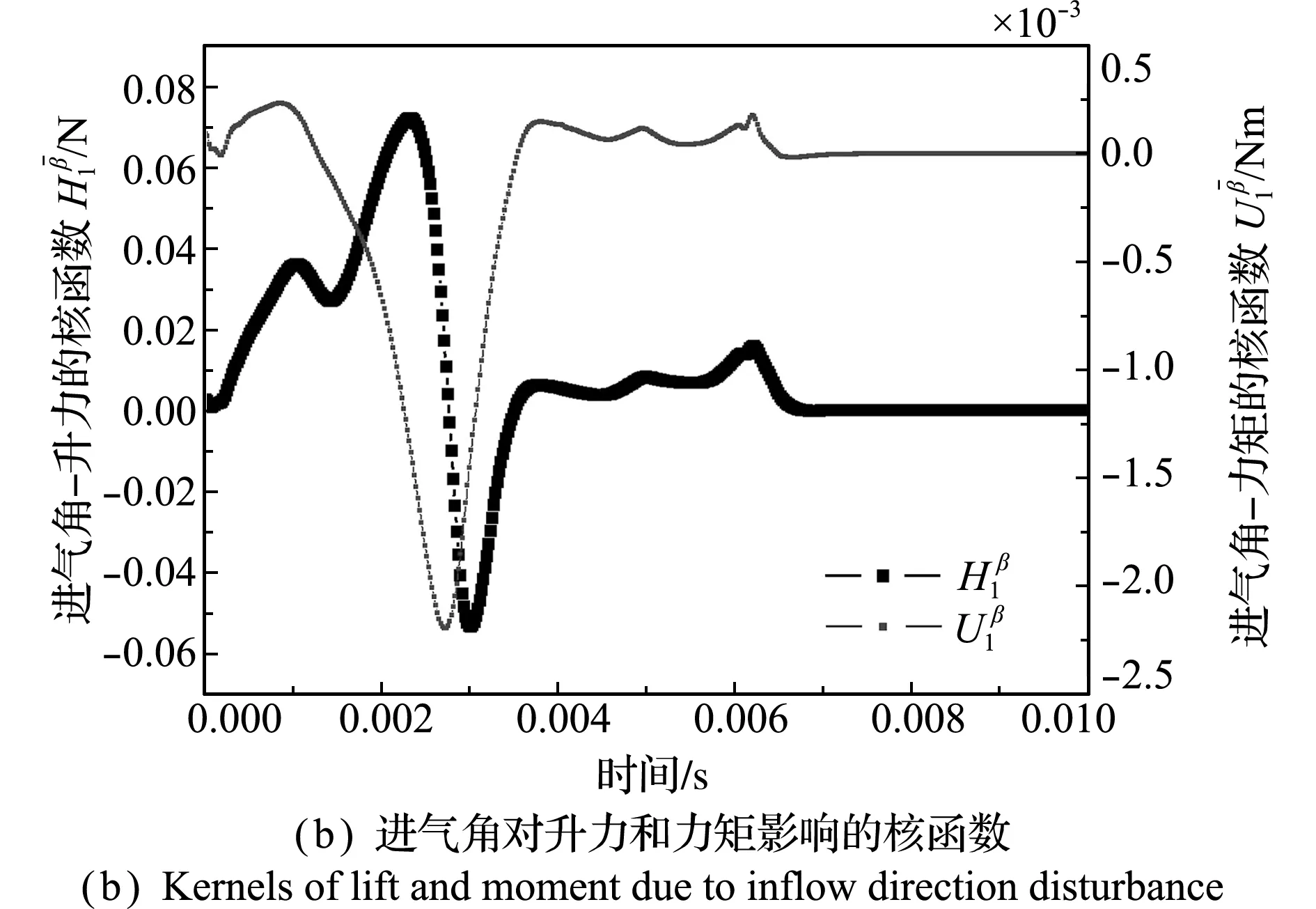
图3 总压和进气角变化引起叶片气动力变化的核函数
Fig.3 Kernels of the aerodynamic forces of the blade due to total pressure and flow direction disturbances
图4和图5给出了一组真实尾流数据,该数据减去了稳态值。用所建立的气动力降阶模型计算这组尾流下叶片的气动力,结果如图6和图7所示,该组数据也减去了稳态值。为方便比较,图中给出了在这组尾流下CFD模型计算得到的叶片气动力。可以看出,降阶模型计算出的气动力与CFD模型的结果基本一致,振幅和频率完全相同。说明该降阶模型的方法能够预测尾流对叶片气动力的影响。需要指出的是,该降阶模型的计算时间少于1 s,而CFD模型的计算时间大于24 h。该方法非常适合需要反复迭代的叶片结构优化设计。
从图6和图7可以看出,降阶模型的结果整体偏离均值,这与降阶模型核函数的精度有关。虽然流场是弱非线性系统,但稳态值和识别信号的选择会对降阶模型核函数的精度有一定的影响。图8 给出了用不同稳态总压(111.3 kPa,118 kPa和120.5 kPa)和识别信号(1 kPa,2 kPa和3 kPa)的核函数计算得到的叶片升力。可以看出,虽然用不同核函数计算得到的气动力基本相同,但精度存在差异,需要进一步研究。

图4 尾流进口总压随时间的变化规律
Fig.4 Time -history of total pressure of a wake
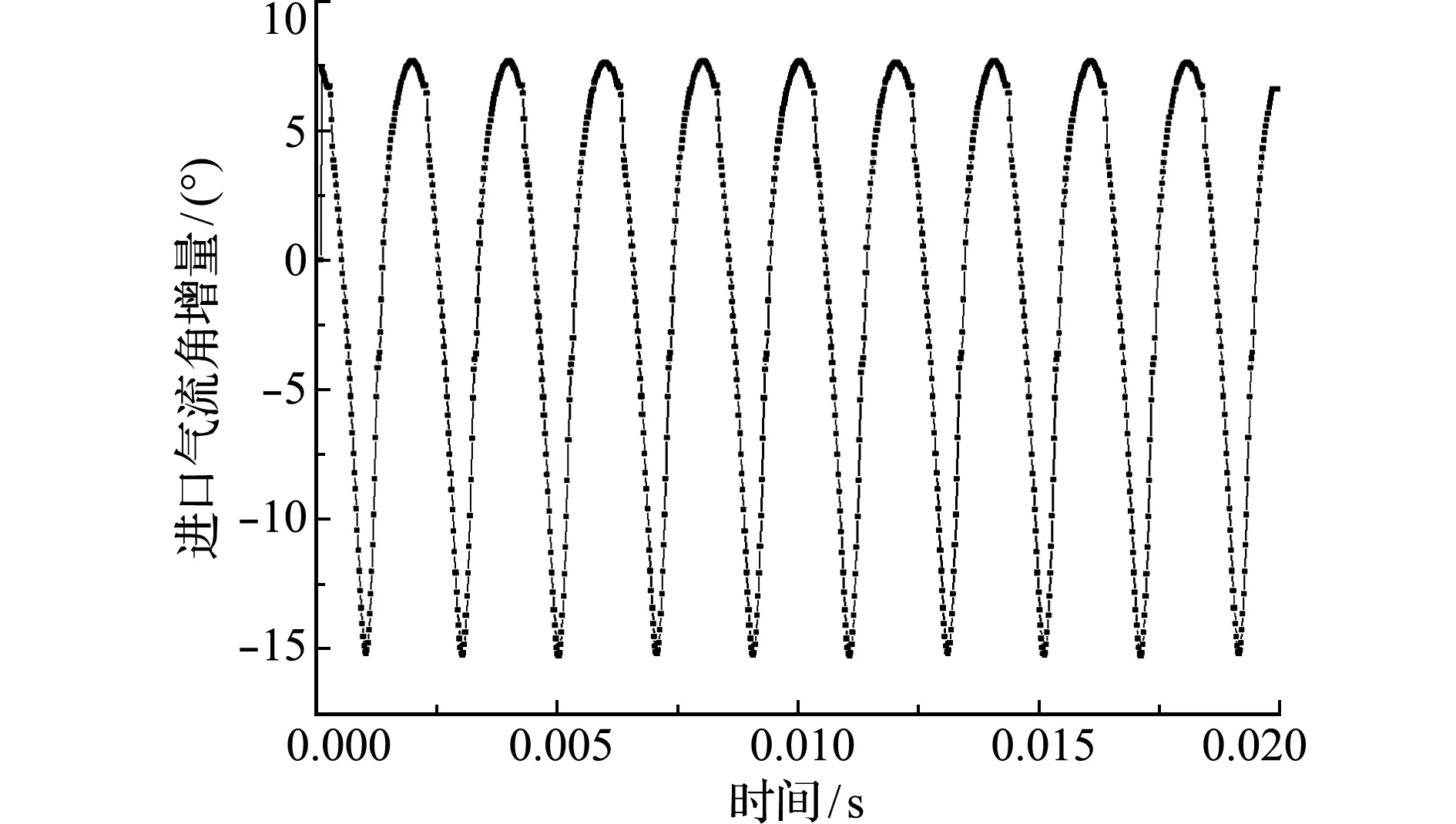
图5 尾流进气角随时间的变化规律
Fig.5 Time -history of inflow direction of a wake
将本文建立的气动力降阶模型和已有的自振激励的气动力降阶模型[8-17]耦合,得到尾流和自振激励的叶片气动力降阶模型,
(5)
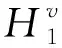
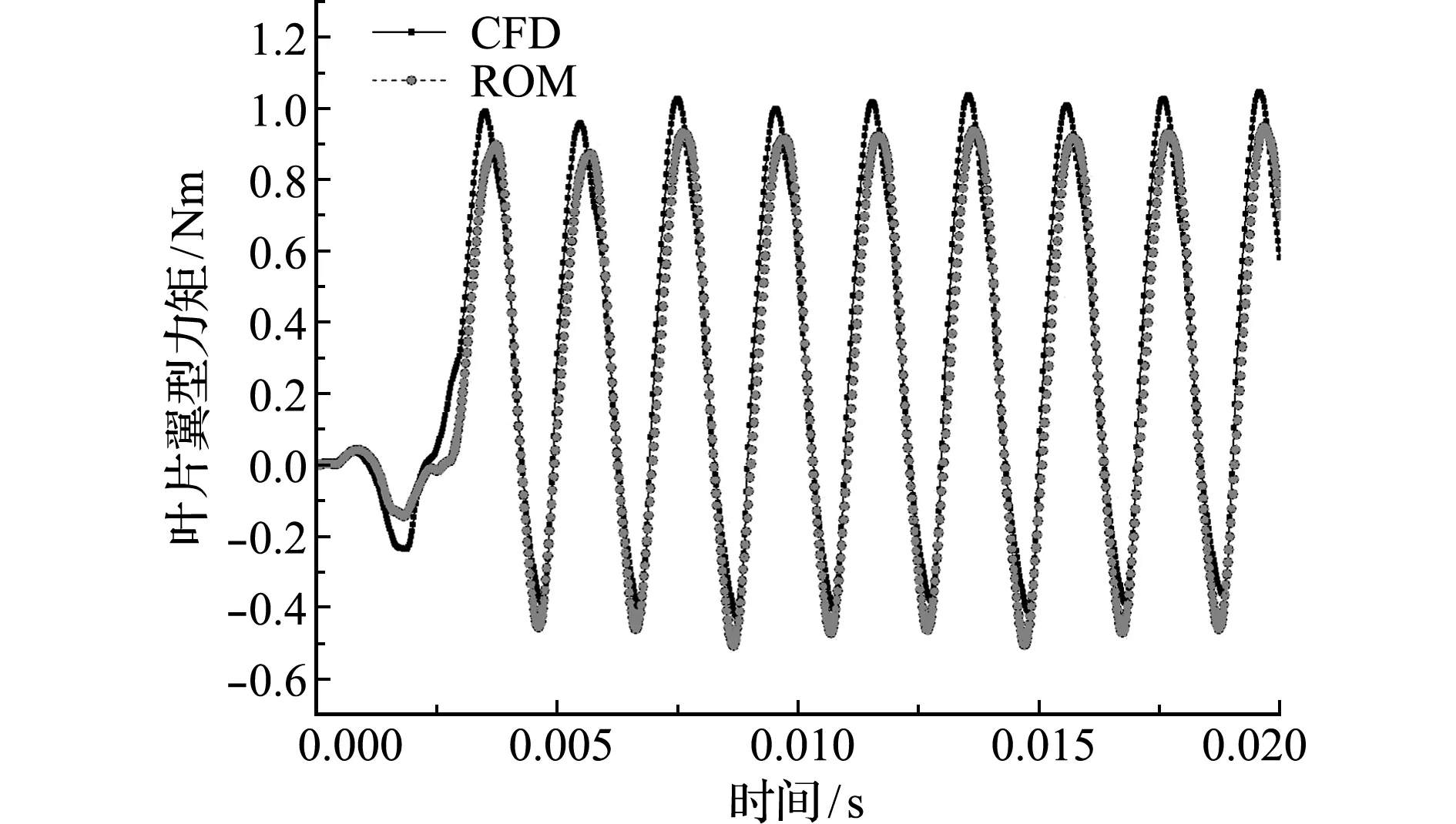
图6 尾流作用下叶片气动力矩的时间变化规律
Fig.6 Time -history of blade moment due to wake

图7 尾流作用下叶片气动力升力的时间变化规律
Fig.7 Time -history of blade lift due to wake

图8 稳态总压和识别信号对核函数精度的影响
Fig.8 Influence of the steady total pressure and identification signals on the accuracy of the kernels
将式(5)的气动力代入叶片结构振动方程,计算叶片振动位移,如图9所示。可以看出,叶片的振动频率与气动力的频率一致,说明在尾流的激励下叶片出现了受迫振动;叶片结构振幅在逐渐收窄,说明初始突加载荷的影响正在逐渐消失,叶片-流场耦合系统稳定,不会发生颤振。
为方便比较,图9也给出了用CFD模型和结构振动方程耦合求解得到的叶片振动位移。可以看出,该位移与降阶模型的结果基本一致;随着时间的增大,采用气动力降阶模型计算得到的位移误差增大。结合图6和图7的结果可知,这是由于气动力降阶模型存在一定的误差,而误差随着时间的推移正在逐渐积累。因此,应当进一步提高气动力降阶模型的精度。
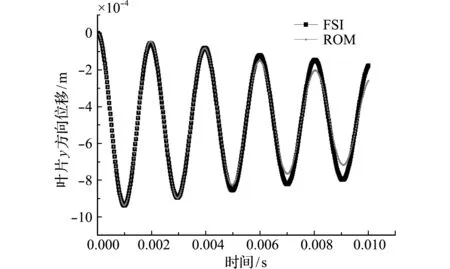
图9 叶片y向位移的时间变化规律
Fig.9 Time -history of heave of the blade
4 结 论
气动力降阶模型是一种高效的气动弹性振动分析方法,现有的气动力降阶模型的研究主要集中在叶片颤振方面,没有涉及上游尾流激励的叶片振动问题。本文基于一阶离散格式的多输入多输出Volterra级数,建立了尾流激励的叶片气动力降阶模型,用于预测上游尾流引起的叶片气动力。
用流场进口的总压和进气角表示上游尾流,并根据尾流的时变是由于上下游叶片的相对转动,用行波法将尾流输入简化为进口上一个点的总压和进气角,并用阶跃信号法识别了核函数。
通过提出的方法建立了一个描述二维叶片气动力和上游尾流关系的降阶模型,并计算了一组真实尾流下叶片的气动力。与CFD的结果对比表明,该降阶模型的结果与CFD的结果基本一致,振幅和频率完全相同,说明本文的方法可行。
另外,气动力降阶模型计算时间少于1 s,而采用CFD模型的计算时间大于24 h。所以,本文的尾流激励的叶片气动力降阶模型非常适用于需要反复迭代的叶片结构优化设计。
:
[1] 赵养正,刘前智,廖明夫.非均匀栅距对压气机叶片非定常气动力的影响[J].推进技术,2007,28(2):167-169,180.(ZHAO Yang-zheng,LIU Qian-zhi,LIAO Ming-fu.Effects of uneven blade spacing on unsteady blade forcing in an axial compressor[J].JournalofPropulsionTechnology,2007,28(2):167-169,180.(in Chinese))
[2] 肖大启,郑 赟,杨 慧.轴向间距对转子叶片气动激励的影响[J].航空动力学报,2012,27(10):2307-2313.(XIAO Da-qi,ZHENG Yun,YANG Hui.Effect of axial spacing on aerodynamic excitation of rotor blade[J].JournalofAerospacePower,2012,27(10):2307-2313.(in Chinese))
[3] 杨 慧,李振鹏.转静干涉对转子叶片颤振特性的影响[J].北京航空航天大学学报,2016,42(2):258-264.(YANG Hui,LI Zhen-peng.Influence of rotor-stator interaction on rotor blade flutter characteristics[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2016,42(2):258-264.(in Chinese))
[4] 张成安,叶正寅,刘 锋,等.进口导流叶片对转子叶片颤振特性的影响[J].推进技术,2010,31(3):335-339.(ZHANG Cheng-an,YE Zheng-yin,LIU Feng,et al.Investigations on flutter characteristics of rotor blade with IGV/fan interactions[J].JournalofPropulsionTechnology,2010,31(3):335-339.(in Chinese))
[5] 赵振华,陈 伟,陈 敏.对转涡轮低压转子叶片的流固耦合数值分析[J].机械科学与技术,2012,31(9):53-57.(ZHAO Zhen-hua,CHEN Wei,CHEN Min.Numerical analysis of low pressure rotor blade using fluid-structure interaction method in counter-rotating turbine[J].MechanicalScienceandTechnologyforAerospaceEngineering, 2012,31(9):53-57.(in Chinese))
[6] Zhao Z H,Lü W L,Chen W,et al.Vibration numerical analysis of counter-rotating turbine with wake-flow using fluid-structure interaction method[J].TransactionofNanjingUniversityofAeronautics&Astronautics,2011,28(1): 66-72.
[7] LI P,Zhao Q J,Zhu Q X.CFD calculations on the unsteady aerodynamic characteristics of a tilt-rotor in a conversion mode[J].ChineseJournalofAeronautics,2015,28(6):1593-1605.
[8] Silva W A.Reduced-order models based on linear and nonlinear aerodynamic impulse responses[A].40t hStructures,Structural Dynamics,and Naterials Conference[C].St.Louis,Missouri,1999.
[9] 周 强,陈 刚,李跃明.基于CFD降阶的非线性气动弹性稳定性分析[J].振动与冲击,2016,35(16):17-23.(ZHOU Qiang,CHEN Gang,LI Yue -ming.Nonlinear aeroelastic stability analysis based on CFD reduced order models[J].JournalofVibrationandShock,2016,35(16):17-23.(in Chinese))
[10] Balajewicz M,Nitzsche F,Feszty D.Application of multi-input volterra theory to nonlinear multi-degree-of-freedom aerodynamic systems[J].AIAAJournal,2010,48(1):56-62.
[11] Wang Y H,Han J L.Approach to identification of a second-order volterra kernel of nonlinear systems by tchebyshev polynomials method[J].ResearchJournalofAppliedSciences,EngineeringandTechnology,2013,5(20):4950-4955.
[12] 张伟伟,苏 丹,张陈安,等.一种基于CFD的叶轮机非定常气动力组合建模方法[J].推进技术,2012,33(1): 37-41.(ZHANG Wei-wei,SU Dan,ZHANG Chen-an,et al.A CFD -based compositional methodo -logy of unsteady aerodynamic modeling for turbomachinery[J].JournalofPropulsionTechnology,2012,33(1): 37-41.(in Chinese))
[13] Su D,Zhang W W,Ma M S,et al.An efficient coupled method of cascade flutter investigation based on reduced order model[A].49t hAIAA/ASME/SAE/ASEE Joint Propulsion Conference [C].San Jose,CA,2013.
[14] Liou M S,Yao W G.Flutter analysis for turboma-chinery using volterra series[A].ASME Turbo Expo 2014:Turbine Technical Conference and Exposition[C].Düsseldorf,Germany,2014.
[15] Ekici K,Kielb R E,Hall K C.The effect of aerodynamic asymmetries on turbomachinery flutter[J].JournalofFluidsandStructures,2013,36(1):1-17.
[16] 张伟伟,叶正寅.基于气动力降阶模型的跨音速气动弹性稳定性分析[J].计算力学学报,2007,24(6):768-772.(ZHANG Wei-wei,YE Zheng-yin.Transo-nic aeroelastic analysis basing on reduced order aerodynamic models[J].ChineseJournalofComputationalMechanics,2007,24(6):768-772.(in Chinese))
[17] 窦怡彬,徐 敏,Christian B.基于SCI/ERA方法的高效气动力降阶模型[J].计算力学学报,2012,29(1):19-24.(DOU Yi-bin,XU Min,Christian B.Efficient aero -dynamic reduced-order-model based on SCI/ERA method[J].ChineseJournalofComputationalMechanics,2012,29(1):19-24.(in Chinese))
[18] 刘金琨,沈晓蓉,赵 龙.系统辨识理论及MATLAB仿真[M].北京:电子工业出版社,2013.(LIU Jin-kun,SHEN Xiao -rong,ZHAO Long.SystemIdentificationTheoryandMATLABSimulation[M].Beijng:Publishing House of Electronic Industry,2013.(in Chinese))
.

