基于神经网络的中央空调粒子群优化算法研究

官金兰，赖煜庭，林子豪，欧杰泉

（1.广东农工商职业技术学院基础部，广东广州510507；2.广州市轻工职业学校电商网络部，广东广州510650）

随着全球气候的变迁和空调技术的发展，越来越多的大型建筑物利用中央空调系统来实现室内温度和湿度的调节控制。特别是随着“智慧城市”建设步伐的快速推进，如何围绕智慧城市建设实现中央空调系统的智能控制与节能，这是智慧城市建设中的重要研究课题之一。中央空调系统的优化控制策略研究也是实际中的一个很有普遍意义的重要课题。粒子群优化（particle swarm optimization，PSO）算法，或称微粒群优化算法，是美国心理学家Kennedy和电气工程师Eberhart在1995年共同提出的，其思想来源于鸟类觅食等复杂群体行为，该算法概念简明、实现方便、收敛速度快，是一种高效的随机搜索方法。中央空调系统包含51个变量，需要对这种多变量的系统进行优化，粒子群优化算法即可实现［1］。

本文还用到二进制的粒子群算法，目的是为了通过调整设备状态来获得最优控制策略，而设备状态只有0、1（关、开）两种状态，普通的粒子群算法无法解决含有离散型变量作为输入的优化，二进制粒子群算法（Binary Particle Swarm Optimization，BPSO）则用来优化离散空间的问题，它扩展了PSO算法的应用，现已经广泛应用到各种离散变量优化问题中［2］。

1 数据预处理

本文研究所用到的中央空调系统数据来自于2017年广州市泰迪智能科技有限公司举办的泰迪杯B题附件，该赛题是由广州泰迪智能科技有限公司及美国伊利诺伊大学新加坡高等数字科学中心联合出题，研究对象来源于实际生活，数据正式可靠，研究结论适用实际生活。该系统记录数据的时间刻度为分钟，本文仅选取该中央空调系统其中两天的系统状态数据进行建模研究，将其中2/3的数据用来建立模型，剩下的1/3数据用来检验模型。

首先，对数据进行异常值检测，去除例如设备状态为关闭，功率消耗记录却为较大值等异常数据；其次，将神经网络的输入数据采用峰值法进行归一化处理，即将每一类数据的每一个数据除以该类数据中比该数据大的数据，使每个数据变成0～1的数据，即归一化峰值。从而加快模型的训练速度和收敛速度。

2 模型建立

2.1 神经网络模型

神经网络是逐层构建的，是由神经元互相连接构成的一个非循环的图，也就是说一些神经元的输出会作为其他神经元的输入，另外环路是不允许的，因为这会使得神经网络的前向传播陷入无止尽的循环中。当然，神经元之间的排列是有规律的，通常情况下被构建成层层连接的形式，每一层中又有多个神经元。对于神经网络隐藏层的节点数，至今还没有统一的规范来解决这个问题,一般可以利用下面两个经验公式来确定［3-4］

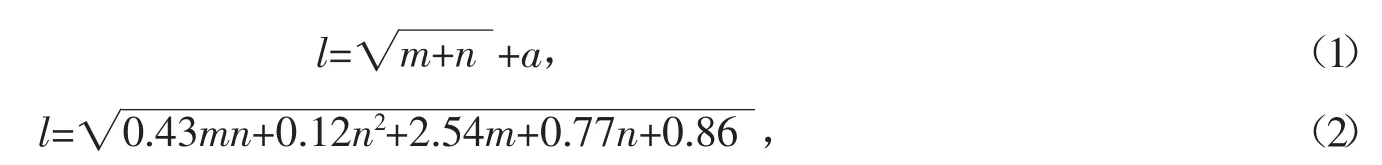
其中，m、n分别为输入节点数目与输出节点数目，a为1～10之间的常数。

本文以基于梯度下降的自适应矩估计方法（Adam）为训练方法，以ReLU函数为神经网络的激活函数建立模型，该模型包含4个隐藏层，每个隐藏层分别包含29、20和15个节点。建立模型的流程图如图1所示。

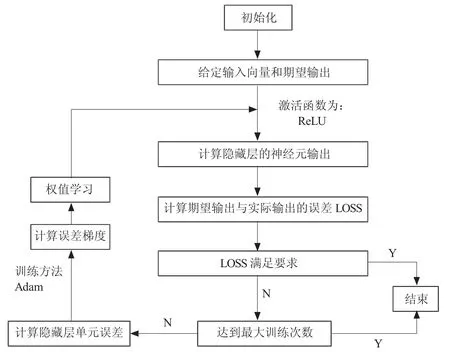
图1 神经网络模型流程

输入层均为全连接层中21个变量（系统中的51个变量去除时间、各设备功率和效率读数）。输出层有3个神经元，分别是热平衡、总耗电量和冷却负载。建立输入变量和3个输出神经元的关系，作为后续优化控制策略的基础。

2.2 粒子群优化算法

粒子群优化算法是从鸟类觅食这种自然现象中得到启发的。它将优化问题的解看作搜索空间的一只鸟，在搜索空间中以一定的速度飞行，这个速度根据它自身及同伴的飞行经验来动态调整。鸟被抽象为没有质量和体积的粒子或微粒，第 i个粒子在维空间里的位置表示为向量 xi=［xi，1，xi，2，…，xi，n］，飞行速度表示为向量 vi=［vi，1，vi，2，…，vi，n］。每个粒子都有一个由被优化函数决定的适应值，并且知道个体历史最优位置 xp→i=［xpi，1，xpi，2，…，xpi，n］，即通常说的粒子个体最优点或个体引导者，这可以看作是粒子自身经验（也被称为认知部分）。此外，每个粒子还知道到目前为止，全体粒子发现的群体历史最优位置即通常说的粒子全局最优点或全局引导者，这个可以看作是粒子同伴的经验。PSO算法是一种基于迭代的优化技术，第t+1次迭代时，粒子将根据自身经验和同伴的经验决定下一步运动的速度和位置。以带惯性权重的基本PSO算法为例，粒子位置和速度的更新公式如下［5］

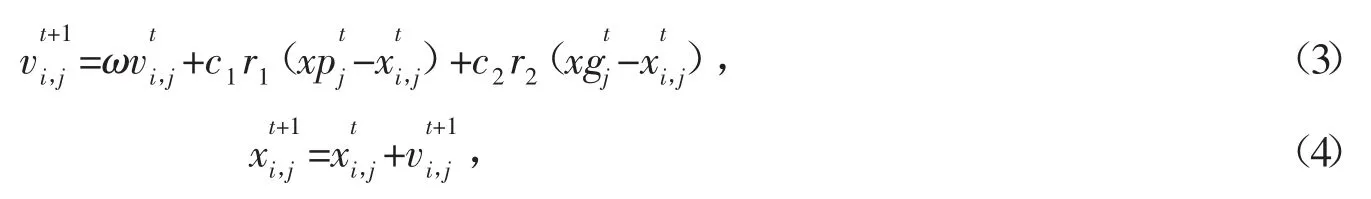
其中，ω为惯性权重，c1和c2为学习因子或称为加速系数，r1和r2为服从均匀分布U（0，1）的随机数，i∈为搜索空间维度，j为粒子规模。粒子位置更新图如图2所示。

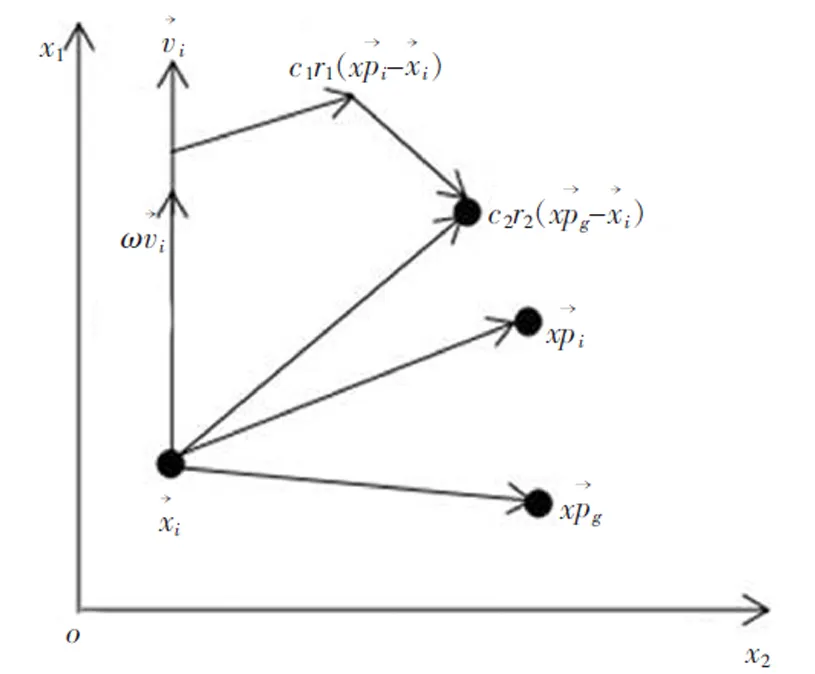
图2 粒子位置更新图

基本PSO算法的简单步骤可以描述如下：

（1）初始化。在决策变量允许范围内随机产生N个粒子的位置，初始化粒子速度为0，粒子个体引导者为

（2）计算每个粒子的适应值，并以此更新粒子的全局引导者；

（3）判断算法是否满足终止条件，若满足，则终止迭代，并输出最优解；

（4）由式（3）和式（4）更新每个粒子的速度和位置；

（5）更新每个粒子的个体引导者，并转入步骤2。

在上述2.1建立的神经网络模型基础上，建立粒子群算法的适应度函数，设一组方案为

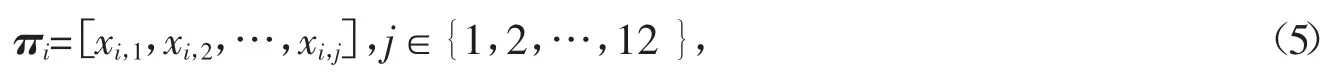
Xij为方案i中第j个设备的开关状态，将神经网络输入层的转速神经元替换为π（xi），得到一个新的输入input（xi）∈R30，input（xi）输入到神经网络中得到输出O，其中

O1，O2，O3分别为执行方案πi时，神经网络预测的系统热平衡系数、系统总功率和冷却负载。定义适应性函数adapt（O）为

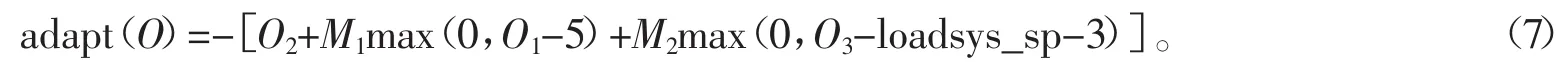
希望找到一个方案，使得系统总功率O2尽量小，系统热平衡系数O1不大于5，冷却负载O3与用户期望的冷却负载设定点相差小于3。

2.3 二进制粒子群算法

二进制粒子群算法中粒子速度的更新公式和普通粒子群算法的速度更新公式为

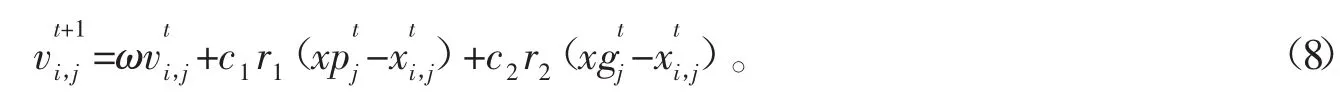
二进制粒子群算法与普通粒子群算法的区别在于其位置更新公式不同，二进制粒子群优化算法将粒子的速度映射到了一个二进制空间，通过下式进行Sigmoid函数转换

生成一个与粒子速度同样维度大小的［0，1］之间的随机数矩阵R并与其相比较，二进制粒子群算法的位置按下式更新

二进制粒子群算法的简单步骤可以描述如下［6］：

（1）初始化。随机产生0或1的随机数作为N个粒子的位置，初始化粒子速度为0，粒子个体引导者为

（2）计算每个粒子的适应值，并以此更新粒子的全局引导者；

（3）判断算法是否满足终止条件，若满足，则终止迭代，并输出最优解；

（4）由式（3）和式（4）更新每个粒子的速度和位置；

（5）更新每个粒子的个体引导者，并转入步骤2。

3 结果分析

3.1 神经网络模型预测结果

本文所建立的神经网络的输出结果有冷却负载、热平衡和系统耗电量。采用交叉检验法对所建模型进行检验，得到所建立神经网络模型的3个输出变量的误差分别是：热平衡误差为1.002 5，耗电量误差为2.452 8 kW，冷却负载误差为1.500 9 RT，所有输出变量的总平均误差为1.652 1，误差较小。由此可见，所建立的模型能较好地模拟出该中央空调系统的运行，有了可靠性较高的模型，再对模型进行优化，从而实现节能的目的。

3.2 粒子群优化算法的优化方案

基于神经网络建立该中央空调的系统模型，再采取粒子群优化算法对系统设备转速进行优化，在满足冷却负载的前提下，优化方案及原系统历史记录的耗电量和系统效率分别如图3和图4所示，其中曲线1为系统历史记录的耗电量和系统效率，曲线2为优化方案的耗电量和系统效率。

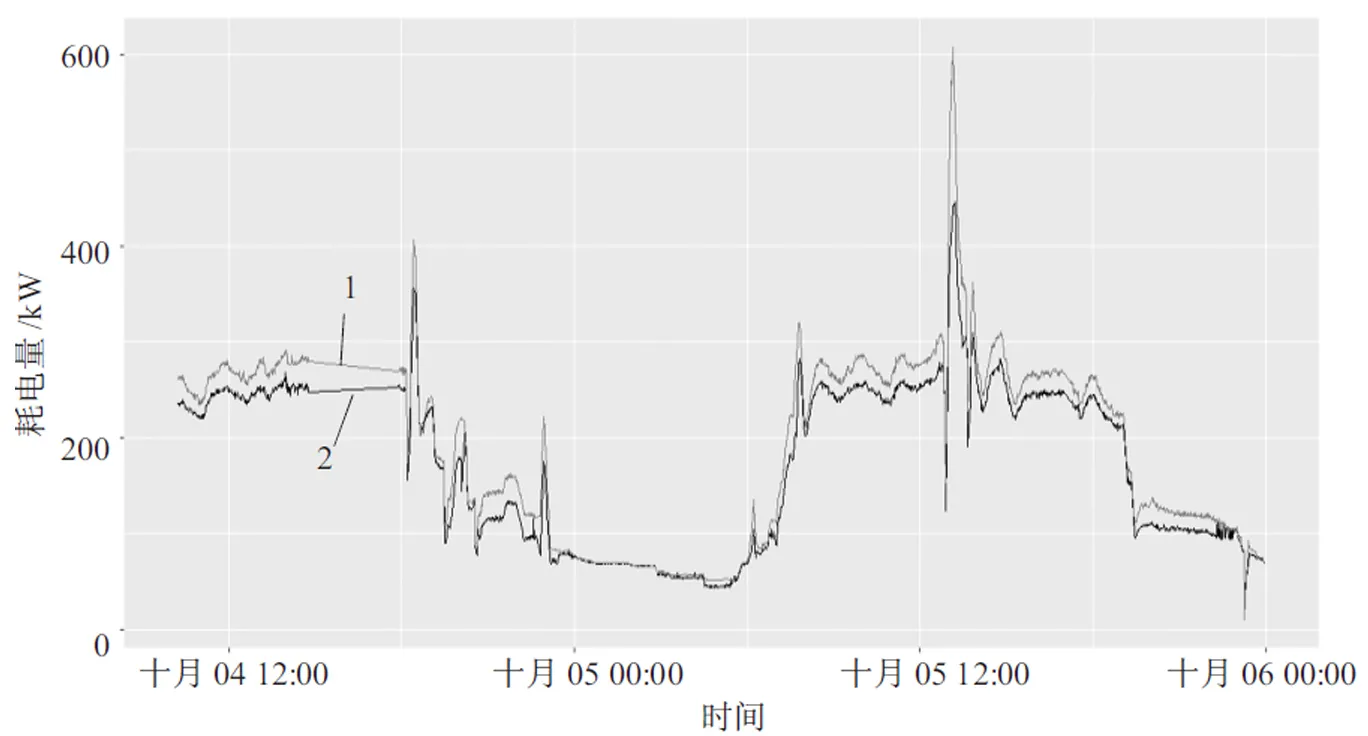
图3 原系统耗电量及优化方案的耗电量

由图3、4可知，优化方案的耗电量少于原系统总耗电量。经过计算，优化方案的总耗电量比历史记录的系统总耗电量减少34 777.22 kW，相比历史记录的总耗电量，节省了9.678 578%的电能消耗，优化方案的系统效率平均提高0.055 619 23，即1 RT的制冷量所需要的电能减少0.055 619 23 kW。

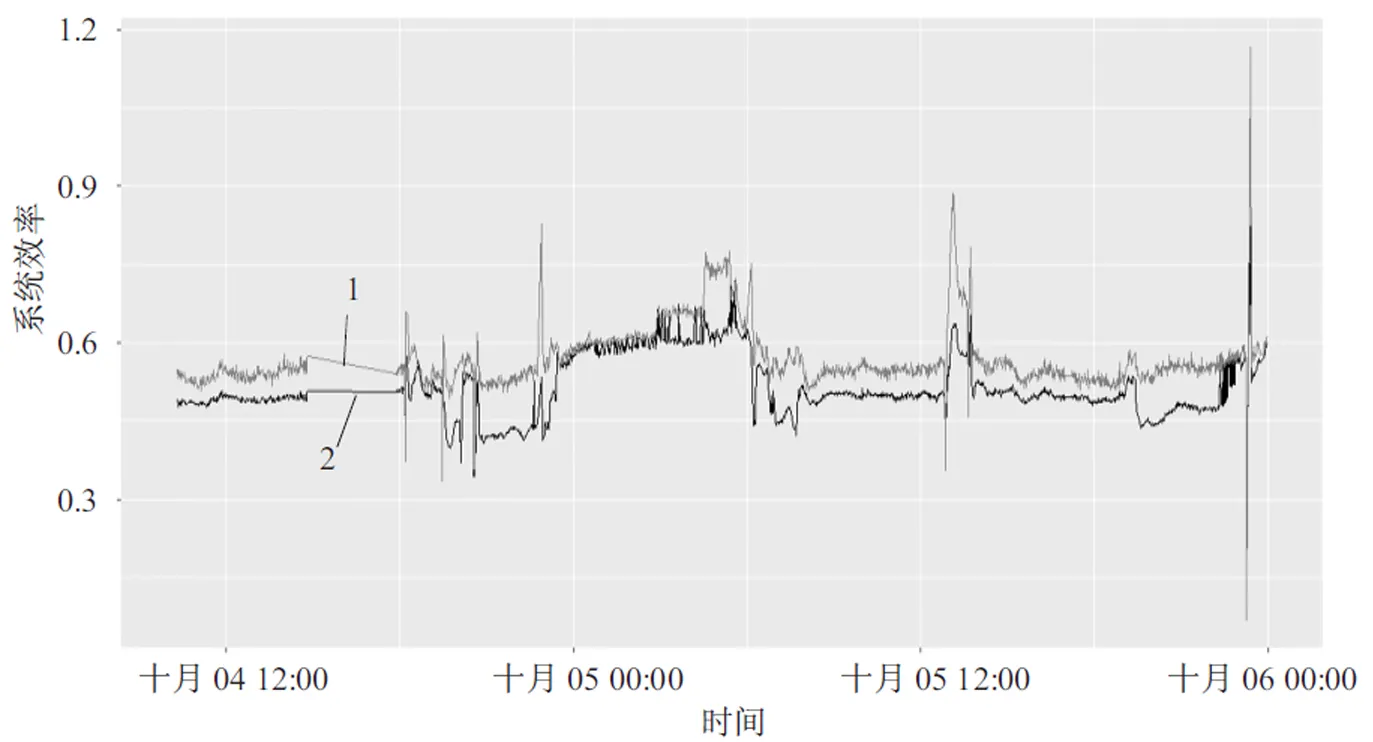
图4 原系统效率及优化方案系统效率

3.3 二进制粒子群优化算法的优化方案

采用二进制粒子群算法对系统开关状态进行优化，在满足冷却负载的前提下，系统优化方案的耗电量及系统历史记录的耗电量和系统效率分别如图5和图6所示，其中曲线1为系统历史记录，曲线2为优化方案的系统耗电量和系统效率。

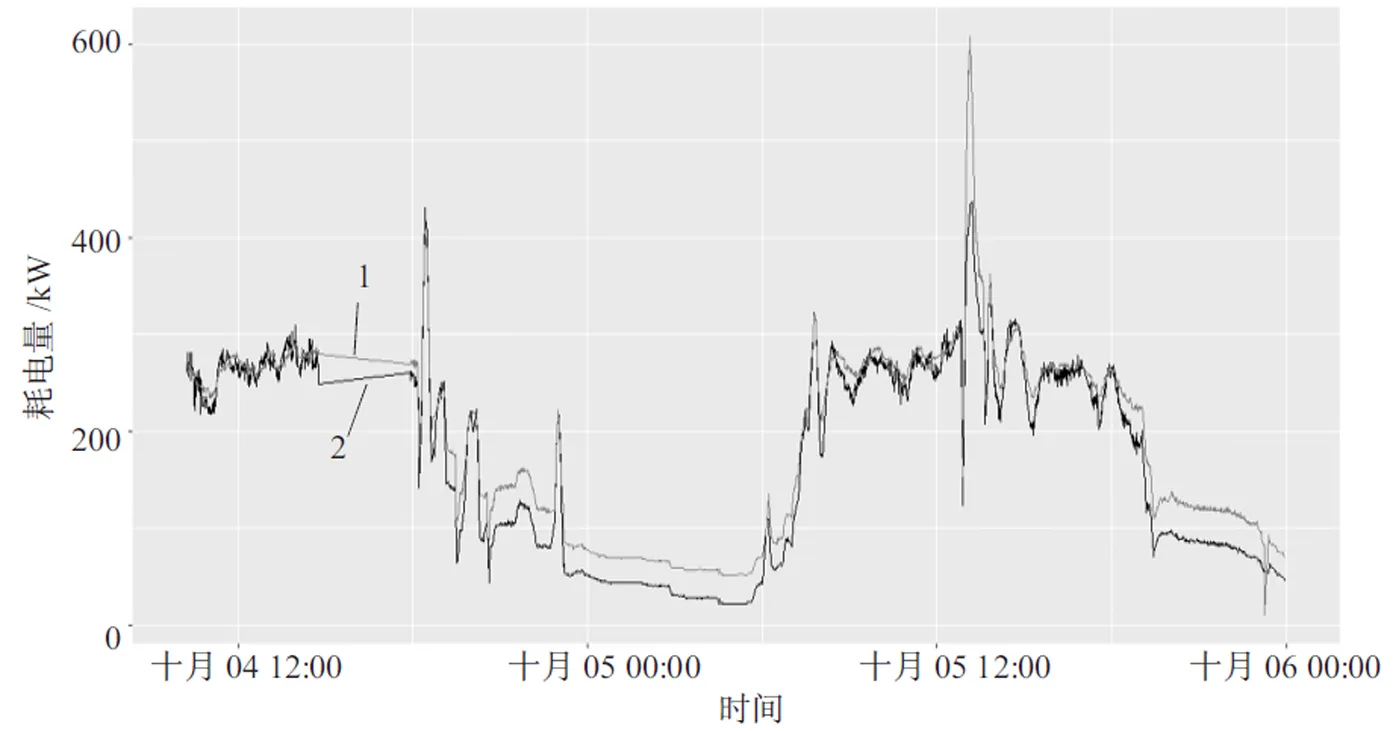
图5 原系统开关状态耗电量及优化系统开关状态耗电量

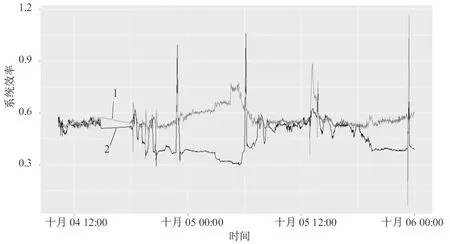
图6 原系统开关状态系统效率及优化系统开关状态系统效率

经过计算，对设备开关状态优化后的优化方案比系统历史记录的总耗电量减少38 234.31 kW，减少10.640 69%的电能消耗，优化方案的系统效率平均降低0.108 748 4 kW，即1 RT的制冷量所需电能减少0.108 748 4 kW。

4 结论与模型改进

4.1 结论

本文利用神经网络建模，进行端到端的参数拟合，避免了特征选择。用交叉检验法检验到所建模型输出变量中的热平衡误差为1.002 5，耗电量误差为2.452 8 kW，冷却负载误差为1.500 9 RT，误差较小。能较好地模拟出该中央空调的运行。为了使该套中央空调系统实现节能目的，用了粒子群优化算法和二进制粒子群算法对模型进行优化，若采用优化方案运行中央空调，可节省10%左右的电能消耗。说明粒子群优化算法和二进制粒子群优化算法对中央空调系统节能控制有一定的效果。

本文的不足之处：1）该中央空调系统的数据是每分钟记录一组的，数据前后是有时间关联的，用神经网络建模就没有利用到这个信息，所以用神经网络建模存在一定的不足。2）粒子群优化算法优化模型存在的弊端就是容易产生早熟收敛（尤其是在处理复杂的多峰搜索问题中），局部寻优能力较差。

4.2 改进方法

神经网络的性能主要由以下几方面决定：神经网络的拓扑结构、神经网络的激励函数、神经网络的训练方法及训练样本的品质。若想降低所建模型的误差，可以采用其他训练方法，如牛顿算法、共轭梯度法和梯度下降法等等；或者选用其他激活函数，如Sigmoid和tanh；或者加大数据预处理的力度，提高数据的品质，减少不良数据对模型的影响，从而降低模型的误差。

［1］张勇,巩敦卫.先进多目标粒子群优化理论及其应用［M］.北京:科学出版社,2016:1-15.

［2］田雨波.粒子群优化算法及电磁应用［M］.北京:科学出版社,2014:120-136.

［3］朱大奇.人工神经网络研究现状及其展望［J］.江南大学学报（自然科学版）,2004,3（1）:103-105.

［4］魏海坤.神经网络结构设计的理论方法［M］.北京:国防工业出版社,2005.

［5］刘衍民,牛奔.新型粒子群算法理论与实践［M］.北京:科学出版社,2013:11-21.

［6］潘峰,李位星,高琪.粒子群优化算法与多目标优化［M］.北京:北京理工大学出版社,2013:15-40.