关于π-余模子余代数的一个注记

陈华喜，鲁 琦

（蚌埠学院理学院，安徽蚌埠233030）

Hopf代数是代数学的新分支，由于其与李代数、微分几何以及统计物理等学科有着密切联系，所以近些年来一直被广泛地研究，并成为当前研究的热点之一。作为通常的Hopf代数的推广，Hopf π-余代数和Hopf π-代数（其中π为一乘法群）自V.G.Turaev引进以来，已经得到广泛地关注和研究。2002年，Virelizer A［1］研究了 Hopf π-余代数的一些重要性质；2004 年，WANG Shuanhong［2］首次提出了 π-H-余模代数的概念，并在此基础上讨论了与π-H-余模代数相关的Maschke-type定理；2006年，WANG Shuanhong［3］又研究了 Hopf π-余代数的π-Galois扩张及Morita Context；紧接着在 2007年，WANG Shuanhong［4］进一步研究了 Hopf π-余代数与余拟三角 Hopf π-代数有关的 Drinfeld co-double；2009 年，赵士银等［5］研究了Hopf π-余理想的相关重要性质。

本文首先引进了π-H-余模余代数以及π-H*-模代数等概念，然后给出了局部有限维的π-H-余模余代数与π-H*-模代数间的对偶关系，接着又引进了π-H-余模子余代数以及π--模理想的概念，最后给出并证明了Hopf π-余代数上的π-余模余代数的一簇子空间J构成Hopf π-余代数上π-H-余模子余代数的充要条件。

在本文中，约定π表示单位元为1的任一乘法群，K表示一个域，所涉及到的向量空间均为K向量空间，所有的映射均为K-线性映射，且A⊗KB写成A⊗B。除特殊说明外，在本文中涉及到的π-（余）模均指的是右π-（余）模。有关π-余代数、π-代数、π-H-余模同态以及π--模同态等定义可参考文献［1］和［6］。下面给出本文中所涉及到的Hopf π-余代数、Hopf π-代数、π-H-余模以及π--模的定义。

定义1［1］设H=（｛Hα｝α∈π，Δ，ε）为π-余代数，给定一簇K-线性映射S=｛Sα│Hα→Hα-1｝α∈π（反极元），若满足以下 3 个条件：1）对任意的 α∈π，（Hα，mα，uα）是 K-代数；2）对任意的 α，β∈π，K-线性映射 Δα，β∶Hα，β→Hα⊗Hβ和 ε∶H1→K都为代数同态；3）对任意的

则称 H=（｛Hα，mα，uα｝α∈π，Δ，ε，S）为 Hopf π-余代数。

注 由此可见，Hopf π-余代数是Hopf代数的一种推广。

定义2［6］设=（｛α｝α∈π，m，u）为π-代数，给定一簇K-线性映射s=｛sα∶α→α-1｝α∈π（反极元），若满足以下3个条件：1）∀α∈π，｛H~α，Δα，εα｝是K-余代数，记Δα（h）=∑h（1，α）⊗h（2，α）∈α⊗α，∀h∈α；2）对任意的 α，β∈π，K-线性映射，u∶K→1和 mα，βα⊗β→α，β都为余代数同态；3）对任意的 α∈π，则称为 Hopf π-代数。

注 当π=｛1｝，此时Hopf π-代数就是通常意义下的Hopf代数。

定义 3［1］设 H=（｛Hα｝α∈π，Δ，ε）是一个 π-余代数，若存在一簇 K-向量空间 M=｛Mα｝α∈π，以及一簇K-线性映射 ρ=｛ρα，β∶Mαβ→Mα⊗Hβ｝α，β∈π，使得对于任意的 α，β，γ∈π，下式成立

则称（M，ρ）为H上的π-余模，记作π-H-余模M。

注 （1）对任意 m∈Mαβ，α，β∈π。

（2）对于任意的 α，β，γ∈π，m∈Mαβγ，式（1）可写成可记为这样的记号可推广到 n 个分量的情形。

定义 4［6］设是一个 π-代数，若存在一簇线性空间 P=｛Pα｝α∈π，以及一簇 K-线性映射且使得对于任意的 α，β，γ∈π，下式成立

则称（P，ηP）为上的 π-模，记作 π--模 P。

以下讨论中，所涉及到的Hopf π-余代数以及π-余模均指的是局部有限维的。其中局部有限维的π-余模M=｛Mα｝α∈π是指其每一个K-向量空间Mα（∀α∈π）都是有限维的。

首先引入映射：如果 H=（｛Hα｝α∈π，Δ，ε）是一个 π-余代数，由Δα，β∶Hαβ→Hα⊗Hβ，ε∶H1→K 可以导出映射和ε*∶K*→H1*，记映射其中是合成映射Hα*⊗记映射是合成映射

定义 5 设 H=（｛Hα｝α∈π，Δ，ε，S）是一个 Hopf π-余代数，C=（Cα，Δ'α，ε'α）α∈π是一簇余代数，其中余代数 Cα的余乘法为 Δ'α（c）=∑c（1，α）⊗c（2，α），∀c∈Cα，α∈π。若存在一簇 K-线性映射 ρ=｛ρα，β∶Cαβ→Cα⊗Hβ｝α，β∈π，且使得下列条件成立：

（1）C=｛Cα｝α∈π，ρC=｛ρCα，β｝α，β∈π是一个 π-H-余模；

（2）对于任意的即对于任意的 c∈Cαβ，有

（3）对于任意的其中

则称为 π-H-余模余代数。

注 两个 π-H-余模的张量积 C⊗C=｛Cα⊗Cα｝α∈π仍然是一个 π-H-余模，其中映射为该余模作用结构映射［6］。

定义 6 设是一个 Hopf π-代数，若存在一簇代数 A=｛Aα，m'α，u'α｝α∈π，以及一簇K-线性映射且使得下列条件成立：1）是一个-模；2）对于任意的；3）对于任意的，其中则称为 π--模代数。

注 两个π-H-模的张量积A⊗A=｛Aα⊗Aα｝α∈π还是一个π--模，其模作用结构映射为

引理 1 设=（｛α｝α∈π，m，u，s）是一个 Hopf π-代数，A=｛Aα，m'α，u'α｝α∈π是一簇代数，且 A 是 π--模，则A成为π--模代数的充分必要条件为下面两个交换图成立

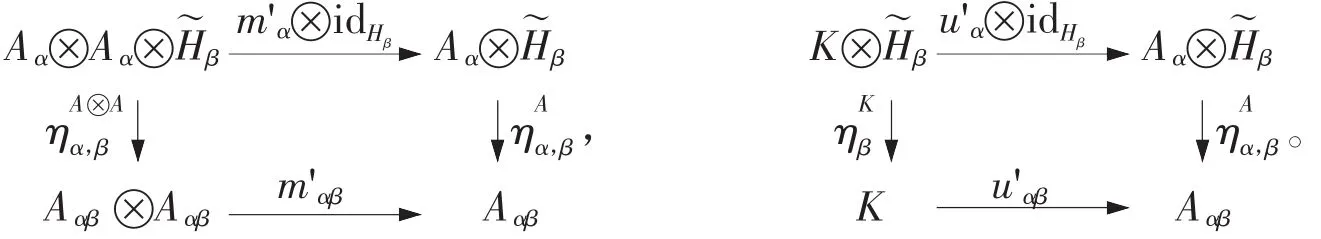
证明 由定义6中条件2），3）可得证。

引理 2［4］设 H=（｛Hα，mα，uα｝α∈π，Δ，ε，S）是一个局部有限维的 Hopf π-余代数，则是一个 Hopf π-代数，其中映射是映射的合成；映射是映射的合成。

定理 1［7］设 H=（｛Hα｝α∈π，Δ，ε，S）是 Hopfπ-余代数，则 H 上的 π-H-余模余代数 C=（｛Cα｝α∈π，ρ=｛ρα，β｝α，β∈π）的对偶是一个 π-H*-模代数。

定义7 设M是π-余代数C的一个π-余模，N=｛Nα｝α∈π是一簇向量空间，Nα是Mα的子空间（其中，α∈π），并且ρα，β（Nαβ）⊂Nα⊗Cβ（其中，α，β∈π），则称N是M的一个π-H-子余模。

定义 8 设 H=（｛Hα｝α∈π，Δ，ε，S）是一个 Hopf π-余代数，C=（｛Cα，Δ'α，ε'α｝α∈π，ρ=｛ρα，β｝α，β∈π）是 π-H-余模余代数，J=｛Jα│Jα⊆Cα｝α∈π是 C 的一簇子余代数（即对任意的 α∈π，Jα是 Cα的子余代数），且 J是 C的π-H-子余模，则称J是C的一个π-H-余模子余代数。

设 A=｛Aα｝α∈π是一簇代数，D=｛Dα│Dα⊆Aα｝α∈π是 A=｛Aα｝α∈π的一簇子空间，若对于任意 α∈π，Dα都是 Aα的理想，则称 D=｛Dα｝α∈π是 A=｛Aα｝α∈π的一簇理想。

定义 9 设是一个 Hopf π-代数，为 π--模代数。D=｛Dα│Dα⊆Aα｝α∈π是 A 的一簇理想，且 D=｛Dα│Dα⊆Aα｝α∈π是 A 的 π--子模，则称 D 是 A 的一个的π--模理想。

引理 3［7］设 C=｛Cα｝α∈π是一簇代数，且 Cα都是有限维的，J=｛Jα│Jα⊆Cα｝α∈π是 C=｛Cα｝α∈π的一簇子空间，则J是C的一簇子余代数的充要条件为J⊥=｛J⊥｝α∈π是C*的一簇理想。

引理 4 设 H 为 Hopf π-余代数，（M，ρ）为 π-H-余模，N=｛Nα｝α∈π是 M=｛Mα｝α∈π的一簇子空间，则 N是M的一个π-H-子余模的充分必要条件为N⊥是M*的一个π-H*-子模。

证明 对任意的 α，β∈π，a∈Mα*，b∈Mβ*，c∈Mαβ，若设 I=｛iα｝α∈π，其中 iα∶Nα→Mα为嵌入映射，显然可得 ρα，βiαβ=（iα⊗idHβ）ρα，β，即 I=｛iα｝α∈π为 π-H-余模同态。考虑 I*=｛iα*｝α∈π，其中 iα*∶Mα*→Nα*为 iα的对偶映射，则有所以即 I*=｛iα*｝α∈π为 π-H*-模同态。

又由于且即 Nα⊥=再由所以即N⊥是M*的一个π-H*-子模。

定理 2 设 H=（｛Hα｝α∈π，Δ，ε，S） 是一个 Hopf π-余代数，C=｛Cα｝α∈π是一个 H 上的 π-余模余代数，J=｛Jα│Jα⊆Cα｝α∈π是 C=｛Cα｝α∈π的一簇子空间，则 J 是 C 的 π-H-余模子余代数的充要条件为 J⊥=｛J⊥｝α∈π是 C*的 π-H*-模理想。

证明 由于 H=（｛Hα｝α∈π，Δ，ε）为局部有限维的 Hopf π-余代数，根据文献［8］知，H*是一个局部有限维的Hopf π-余代数。

由定理1可知，H上的π-H-余模余代数C的对偶C*是一个π-H*-模代数，再由引理3知，J是C的一簇子余代数的充要条件为J⊥=｛J⊥｝α∈π是C*的一簇理想；最后，由引理4知，J是C的一个π-H-子余模的充分必要条件为J⊥是C*的一个π-H*-子模。

综上可知，J是C的π-H-余模子余代数的充要条件为J⊥=｛J⊥｝α∈π是C*的π-H*-模理想。

［1］VIRELIZER A.Hopf group-coalgebras［J］.Journal of Pure and Applied Algebra,2002,171（1）:75-122.

［2］WANG Shuanhong.A Maschke type theorem for Hopf π-comodules［J］.Tsukuba J Math,2004,28（2）:377-388.

［3］WANG Shuanhong.Morita Contexts,π-Galois extension for Hopf π-coalgebras［J］.Communications in Algebra,2006,34（2）:521-546.

［4］WANG Shuanhong.Coquasitriangular Hopf group algebras and Drinfeld co-doubles［J］.Communications in Algebra,2007,35（1）:77-101.

［5］赵士银,孙建华.Hopfπ-余理想［J］.西南师范大学学报（自然科学版）,2009,34（3）:32-35.

［6］孙建华,苏航赟.π-余模代数与 π-张量积［J］.扬州大学学报（自然科学版）,2010,13（1）:1-9.

［7］陈华喜,殷晓斌.Hopfπ-余模余代数的对偶［J］.山东大学学报（理学版）,2011,46（12）:46-50.

［8］赵士银.Hopfπ-余代数与单侧π-余理想［J］.山东理工大学学报（自然科学版）,2008,29（2）:163-165.