梁格法在城市桥梁设计中的应用分析

季 冬 良

(上海林同炎李国豪土建工程咨询有限公司苏通分公司，江苏 南通 226000)

0 引言

随着我国城市化迅速发展，城市的基础设施建设越来越多，相应的高架桥梁和立交桥梁不断涌现。为了满足城市日益增长的交通运输需求，桥梁的桥面宽度在不断地增加相应的新型结构型式也在不断发展，为了确保设计的桥梁结构型式能够满足运营寿命和使用安全要求，需要对桥梁结构计算分析进行准确把控。城市高架桥和立交桥中的宽梁桥、斜交桥和曲线桥等结构型式，采用传统的平面杆系模型其实无法准确计算荷载横向分布、横向支座反力及其他内力集中效应，然而采用梁格理论可以很好地解决上述难题。

长期以来杆系模型广泛用于桥梁的总体结构分析中，虽然具有计算简单、分析明确的优势，但不能满足目前精细化结构设计需求，往往对内力(应力)集中等问题较难回答。实体计算理论又因为单元数量多所需要的计算代价较高，而梁格法则是介于其中的实用有效计算理论，具有概念清晰、易于理解和使用方便等特点。梁格法的基本理念是将桥跨结构分散为梁格体系，实际的构件通过区间划分将其刚度等效到梁格上，通过对梁格分析计算其内力分布和变形，特别适用于城市高架和立交中的宽梁桥、斜交桥和曲线桥等结构型式[1，2]。

本文首先分析梁格法理论的基本原理，明确其理论基础和适用性；其次阐述梁格法中梁格划分方法和单元刚度计算方法，这是梁格法应用的两个重要问题；再则阐述梁格法理论的分析优势和不足；最后通过案例方式阐明梁格法在城市桥梁设计中的应用。

1 梁格法基本原理

梁格法的基本原理是用等效的两个代替该区域的桥跨结构，并通过梁格之间的连接描述划分区域之间梁体的相互关系，实际上梁格法是以梁为基本单元的有限元分析方法，但其相对于传统的杆系模型而言可以较为准确的计算横向受力特性。梁格法的概念明确、容易理解、方法易使用、计算速度快。

具体而言，梁格法将桥跨结构用等效的平面或者空间架构模拟，一般根据结构特点进行架构的划分，每个划分的区段内梁体的抗弯刚度和抗扭刚度直接等效到该梁格架构上，通过该平面/空间架构的分析就可以计算梁体的横向受力、轴向受力和三维变形。对于箱梁截面而言，如果以腹板为单元进行梁格划分，梁格的受力特点可以直接反演到腹板上，这样可以直接进行腹板的配筋和设计，避免了采用空间有限元方法必须要对腹板进行内力横向分布的环节，使得设计简单计算准确。

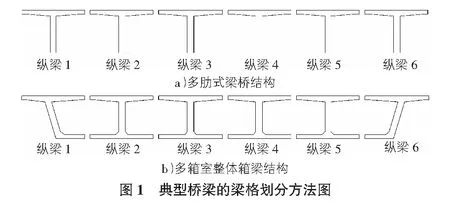
梁格法的关键是梁格划分和单元刚度计算[3]：首先梁格划分需要根据截面特点考虑，例如多肋式梁桥则将每个梁肋视为梁格，多室箱梁则将腹板视为梁格划分标准，如图1所示；其次是单元刚度的计算，应该使得计算的等效梁格体系在单位荷载作用下的变形和内力与原有结构相同，即等效性原则。

2 梁格划分及单元刚度计算

2.1 梁格划分方法

梁格划分应该根据结构形状及支座等进行确定，一般而言梁格划分的一般性原则可以总结如下：

1)梁格划分应尽量符合原型结构的内力分布特点及截面形状，例如多肋式梁桥其受力是每个梁肋承担，因此以梁肋为标准划分；多箱室整体箱梁结构其受力是每个腹板承担剪力流，因此应该以腹板为中心进行梁格划分。

2)梁格划分应尽量重合设计受力线，例如可以根据支座受力线进行梁格划分，有效地模拟结构的受力状态和变形状况。

3)梁格的纵横向间隔应该尽可能一致，使得梁格单元对于荷载作用下的响应特性足够灵敏，如果某一个梁格划分尺寸很小，则在受力分析过程中可能出现奇异矩阵导致计算结果出现误差。

4)梁格模型的划分应该尽量使得各个部分的形心位置和整体形心轴位置重合，使得梁格能够最大程度反映原始结构的受力状态。

2.2 单元刚度计算

根据梁格法基本理论，荷载作用下梁格的受力及变形状态是以单元之间的刚度关系为依据进行分配的，因此梁格法计算的准确性取决于梁格单元是否能够准确模拟原始结构的受力特性。不同的结构形状其单元刚度计算方法也不相同，以下针对典型结构分析其单元刚度的等效计算方法。

对于板式结构，可以按照正交各向同性板计算梁格的等效刚度，如下式所示，计算的依据就是划分区域内梁板的等效抗弯刚度和抗扭刚度。

i=h3/12;c=h3/6。

其中，i为单位板宽情况下构件的惯性矩；c为单位板宽情况下构件的有效抗扭参数；h为板厚。

对于箱梁结构，根据梁格划分原则往往分类为多个工字梁：纵向单元特性的计算就是以工字梁为基础确定其抗弯惯性矩，抗剪则以腹板承担计算其腹板面积作为抗剪面积；横向单元特性的计算则是两块板组成的空腹式截面，因此抗弯惯性矩就是两块矩形板在距离中性轴一定距离下的等效抗弯惯性矩，根据单元荷载作用下变形和受力等效的原则计算其截面特性。箱梁扭转变形时，剪力流往往围绕着顶板、底板和腹板的周边流动，因此抗扭刚度可以认为是顶板和底板提供。

3 梁格法理论的分析优势及不足

梁格法理论只要做好梁格划分及单元刚度计算，其余的计算操作都很简单，操作方便；梁格法相对于单梁计算模型，因为考虑了横梁的刚度贡献和传力效应，因此计算结果相对于单梁模型更加准确，能够分析横梁的受力和变形特点，对于整体结构变形问题估计更加合理；梁格法相对于实体有限元模型计算的单元数量大大减少，且能够根据计算内力情况直接进行配筋设计，因此相对实体有限元方法更加简单实用。总体而言，梁格法特别适用于多肋式和多箱室结构的计算，相对于单梁模型计算结果更加准确且能获得横向构件受力情况，相对于实体有限元模型计算过程更加简单且能直接根据计算结果进行配筋设计。

然而，梁格法理论本身的特点使得其应用存在一定的不足，首先梁格法对于剪力滞问题描述不够准确，虽然其计算结果能够表现顶板不同位置应力水平的差异，但是往往差异不明显，相对于实体有限元结果计算的明显剪力滞问题描述不够；梁格法计算的结构变形和应力状态往往介于单梁模型和实体模型之间，对于局部精细化设计问题采用梁格理论不能代替实体有限元的分析结果。

4 梁格法理论的应用分析

4.1 工程算例

某双跨连续钢筋混凝土实心板桥，桥面宽度12.8 m长度40 m，主体桥面宽8 m高1 m，两侧翼缘分别宽2.4 m高0.4 m，所用混凝土材料的基本参数如下：密度2 600 kg/m3,弹性模量35 GPa,泊松比0.167，采用梁格法计算其结构受力特点，并与实体有限元计算结果进行对比。根据梁格法理论，首先进行梁格划分和单元刚度等效计算，梁格的划分为了保证计算精度按照横向1 m宽度考虑，两侧2.4 m的翼缘则按照1.2 m梁格尺寸确定，纵向尺寸1 m，详细的梁格划分如图2所示，根据划分的梁格单元计算其等效刚度。注意到由于左右两侧翼缘的高度不同，导致其截面形心位置与主体截面存在差异，计算中应该考虑对梁格2～3及10～11设置横向刚性连接，保证两者的受力和变形的一致性。

4.2 计算结果分析

表1是采用梁格法和实体有限元方法计算的自重作用下顺桥向梁体的弯矩结果，可以看到梁格法的计算结果与实体有限元计算结果存在很好的吻合性，误差基本在6%以内，无论是对于整体的弯矩情况还是特殊构件3的弯矩分配，说明了梁格法计算的准确性，用于城市桥梁设计计算具有很好的适用性。

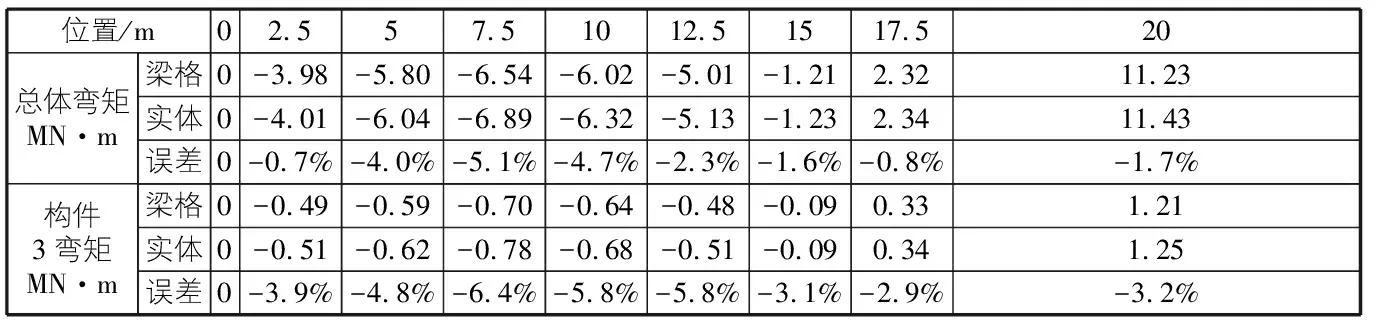
表1 梁格法计算结果与实体有限元结果的对比分析

5 结语

梁格法具有概念清晰、易于理解和使用方便等特点，非常适用于城市高架桥和立交桥中的宽梁桥、斜交桥和曲线桥等结构型式，本文分析了梁格法的基本理论及其关键技术，即梁格划分和单元等效刚度计算两个问题，并总结了梁格法的技术优势和存在的不足，通过工程案例分析了梁格法在城市桥梁设计计算中的应用，并与实体有限元计算结果进行对比，误差在6%以内，具有很好的精度，可以准确地用于城市桥梁的结构分析中。

参考文献:

[1] 王富万,杨文兵.梁格法在桥梁上部结构分析中的应用[J].华中科技大学学报(城市科学版),2006,23(S1):80-82.

[2] 王洪光.梁格法和单梁法在斜桥分析中的应用[J].交通标准化,2007(7):130-132.

[3] 王怀中,吕艳平.论梁格法在立交桥梁设计中的应用[J].广东科技,2013,22(10):137.