基于灰色Verhulst模型的高速公路路基沉降预测研究
郭 凯 武
(中铁十一局集团第二工程有限公司,湖北 十堰 442000)
1 工程概况
张桑高速公路K35+924~K36+063路段主要填料为红砂岩及部分处治过的高液限粘土,属于不佳填料且最大填筑高度31.5 m、原地面起伏较大,有一定的滑坍危险;且K35+934附近有一较大管径的圆管涵,对沉降控制要求更为严格;该路段为填挖交界段,汇水能力较强,也易受降雨影响,因此需对该路段全断面开展施工期沉降观测。
由于中桩位置处受机械振动及碾压次数较两侧多,一般而言中部的沉降量会更大,因此本文计算及分析均选取中桩位置的沉降数据作为分析对象来对断面的沉降情况进行预测。该断面观测点的实测沉降数据与时间、填筑高度关系曲线见图1。

通过观测数据分析可知,当填筑施工开始约400 d、填土高度达28.5 m时,沉降速率在1.0 mm/d~1.2 mm/d范围内,路基较稳定。该路段工期要求在2016年11月初必须进行底基层乃至面层施工,在此之前需要对路基沉降量进行预测,以判定路基沉降是否具备底基层施工条件。
2 沉降预测模型
进行沉降预测时灰色理论应用较多,常见的模型有GM(1,1)模型和Verhulst模型等,GM(1,1)模型在进行沉降预测时,是将所测得的数据进行等时距处理后再作为数据序列进行计算,其基本表现形式为:
由上述表达式可知,该模型具有无限增长的性质,但在进行中长期沉降量预测时,路基沉降不可能无限增大,模型曲线增长变化趋势与实际情况有所不符,存在一定的局限性。 而Verhulst模型表达式呈“S”形曲线,与路基沉降的实际曲线有共通之处且较之GM(1,1)模型,Verhulst模型能够进行中长期预测的原因是其包含了次固结沉降,而在一些以红砂岩和高液限粘土为主的路基中,次固结沉降是路基沉降不能忽略的组成部分,因此Verhulst模型进行工后预测要比GM(1,1)模型更精确。
灰色Verhulst预测模型的微分方程为:
S(0)(k)+aZ(1)(k)=b(Z(1)(k))2。
其白化形式的微分方程为:
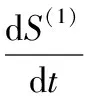
(1)
(2)
其中:
则路基沉降灰色Verhulst预测模型时间响应方程即白化方程为:
(3)
离散响应方程为:
(4)
由于路基变形数据本身就呈“S”形曲线,故可将原始沉降观测数据视为S(1),经一次累减生成新数列为S(0),从而建立灰色Verhulst模型,继而直接拟合S(1)。由式(4)可以看出,当t→∞时,若a>0,有S(1)(t)→0,这是不可能的;若a<0,则S(1)(t)→a/b,a/b即表示路基最终沉降变形量。
3 沉降预测分析
选取该断面中桩实测的第370天~第416天的数据作为时间序列进行分析如表1所示。

表1 路基沉降实测第370天~第416天数据
由于现场实测的路基沉降数据是非等时距的,在建模之前先进行等时距处理,如下所述:
1)计算平均时间间隔:

2)利用拉格朗日插值定理计算等时距各天的沉降值,具体数值见表2。
3)按第2节中式(2),式(3)计算参数a,b:
将表2数据代入式(2),式(3)计算可得出:a=-0.047 2,b=-0.000 1。
得出的预估模型为:

表2 处理后的等时距各天沉降值
将第341天~第359天的实测沉降量和预估模型计算的沉降量进行对比分析,如表3所示。

表3 Verhulst预测值与实测值相对误差值
由表3计算数据可得误差对比图如图2所示。
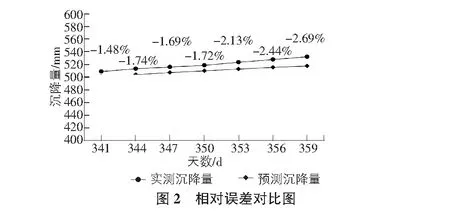
由表3及图2可知,Verhulst模型预测值与实测值相比相对误差较小(3%以内),预测模型较为精确,且该段的预测值要略小于实测值。利用预估模型,按时距3 d,预测第419天~第479天(10月30日)沉降量,计算如表4所示。
由表4计算数据可知,预估该断面10月30日总沉降量为578.81 mm。其日沉降率约为0.66 mm/d。可以认为截止到10月30日,该断面的沉降速率为0.66 mm/d,月沉降速率约为17 mm/月。根据相关文献说明,当路基沉降速率为3 mm/月~5 mm/月时,后期路面出现稳定性不佳引起的病害的可能性会大为减小;而目前该断面若不进行任何处理则截止到11月,其速率
还难以满足,因此要在11月初进行底基层等后续施工则建议进行轻度处理使其达到底基层施工的要求,即可保证更佳的路基施工质量。

表4 Verhulst预测模型计算的第370天~第416天沉降值
4 结语
该断面路基土体以红砂岩和高液限粘土为主,次固结沉降是路基沉降不能忽略的组成部分,路基沉降变形数据呈“S”形曲线。本文采用了Verhulst模型对某一具体路基断面进行了沉降预测,在某一特定时间点下该断面的沉降速率约0.66 mm/d,该速率下进行底基层施工可能会在后期引起部分路面病害,因此建议稍作处理以加速路基的稳定。由此可知,采用Verhulst模型可对路基的后续施工工期确定提供数据参考,对同类工程实际有较好的指导及参考价值。
参考文献:
[1] 王正新,党耀国,刘思峰.无偏灰色Verhulst模型及其应用[J].系统工程理论与实践,2009(10):138-144.
[2] 宋彦辉,聂德新.基础沉降预测的Verhulst模型[J].岩土力学,2003(1):123-126.
[3] 周德强,冯建中.建筑物沉降预测的改进Verhulst模型研究[J].地下空间与工程学报,2011(1):194-198.
[4] 偶昌宝,俞亚南,王战国.不等时距灰色Verhulst模型及其在沉降预测中的应用[J].江南大学学报,2005(1):63-65.
[5] 徐新跃,方德胜.灰色Verhulst模型预测软土地基建筑物的沉降[J].地下空间,2001(S1):515-518,591.

