一种面向运动目标提取的对称交替方向RPCA算法

吴高宇，邵振洲，2，渠 瀛，施智平，3，关 永，2

1(首都师范大学 信息工程学院，北京 100048)

2(成像技术北京市高精尖创新中心，北京 100048)

3(首都师范大学 轻型工业机器人与安全验证北京市重点实验室，北京 100048)

4(田纳西大学 诺克斯维尔分校工程学院，田纳西 美国 37996)

1 引 言

运动目标提取是计算机视觉中基础而又关键的处理步骤[1]，广泛应用于道路交通监控、自动驾驶等领域中.经典的运动目标提取方法有帧差法、背景差分法、光流法等.但是帧差法和背景差分法对背景变化的鲁棒性不好，光流法则计算量较大.同时，随着图像分辨率的提高，数据的冗余度增加，这对算法效率提出了更高的要求[2].

近年来，基于鲁棒主成分分析(Robust Principal Component Analysis，RPCA)的运动目标提取算法有效解决了上述问题，成为该方向的研究热点[3].采用RPCA的方法对运动目标进行提取，这个模型要求前景目标相对整张图片要比较小，这使得该方法的实际运用受到很大限制.后来的研究者对此进行了改进，Candes等人[4]提出用凸规划方法来解决RPCA问题.在这种方法中，作者将低秩与稀疏矩阵的分解等价为如式(1)所示的凸规划问题：

(1)

其中，‖·‖l1为l1范数，‖·‖*为核范数，δ为任意一个大于零的规整化参数，C为要处理的矩阵，x为稀疏矩阵，y为低秩矩阵.式(1)中的最优化问题一般采用迭代阈值技术[5]或加速近端梯度算法(Accelerated Proximal Gradient Descent，APG)[6]解决，收敛速度较慢.后来Lin等人基于增广拉格朗日乘数法(Augmented Lagrange Method，ALM)提出了EALM(Exact Augmented Lagrange Method)和IALM(Inexact Augmented Lagrange Method)[7].然而，这两种方法在求解式(1)时，并没有利用到目标函数与约束条件的可分离结构，影响了算法的提取效果.Yuan 和Yang[8]提出了用交替方向法(Alternating Direction Method，ADM)来求解式(1)，但这种方法在每次迭代过程中需要进行多次奇异值分解(Singular Value Decomposition，SVD)计算，这使得整个算法的计算量很大，耗时较长.同时在迭代求解过程中，由于没有考虑到低秩和稀疏矩阵之间的关系，最后分解的精度也不高.

Zhang等[9]针对变分不等式问题提出的新交替方向法，具有简单易行和计算效率高的特点.在上述方法的启发下，本文提出了一种基于对称交替方向法(Symmetrical Alternating Direction Method，SADM)的运动目标提取算法，其流程图如图1.该算法核心思想是将视频序列中连续的多帧作为输入，每一帧都转换成矩阵C的一列，再将矩阵C通过主成分分析的方法分解成一个稀疏矩阵x和一个低秩矩阵y，x矩阵中每一列对应矩阵C中同列图片的运动目标，y矩阵中每一列则对应背景.SADM根据交替方向法的对称原理[10]，将求解过程中的线性约束乘数在一次迭代中更新两次，这个改变将会使得收敛速度更快，从而减少算法的计算时间.同时，本文在算法中引入了新的停机准则和均衡参数，避免了不必要的迭代，通过将规整化参数δ加入到迭代过程中，使得结果具有更好的分解效果，从而提高目标的提取精度.

图1 整体流程图Fig.1 Overall flow chart

从多帧视频序列组成的矩阵C中提取出运动目标可以等价为求解式(1)的稀疏矩阵x和低秩矩阵y.x包含了运动目标，y则包含了背景.而ADM的求解方法计算量大、耗时长，所以本文采用一种新的方法——SADM来解决式(1).该方法一是改进了ADM的迭代策略；二是将新的均衡参数和停机准则加入到式(1)的迭代求解过程中，接下来做具体介绍.

2 对称迭代策略

针对前文提到的ADM收敛速度较慢的问题，本文在研究该算法的时候发现，在每一次的迭代更新过程中，原方法都只对线性约束乘数Z做了一次更新，而Z作为判别算法收敛的参数，其缓慢的更新速度也是导致算法速度慢的重要原因.针对这一问题，本文采用了一种新的对称迭代策略，以加快Z的更新速度，减少算法的耗时.

通过令f(x)=‖x‖*，g(y)=δ‖y‖l1，式 (1)可以写成：

min{f(x)+g(y)} subj C=x+y

(2)

其对应的拉格朗日方程为[11，12]：

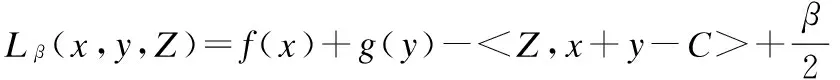
(3)

其中x∈X为稀疏矩阵，y∈Y为低秩矩阵，C为要处理的矩阵，Z∈r是线性约束乘数，< >为标准跟踪内积，‖ ‖是诱导F范数，β>0为罚参数，方程定义域为U=X×Y×r.

对于式(2)，原ADM求解过程为：

(4)

其中xk，yk，Zk分别表示第k次迭代时的值，L(xk，yk，Zk)代表对应的拉格朗日方程，Z∈r是线性约束乘数.这种方法虽然利用了所给条件的可分离结构这一特点，但是在求解y时，会多次用到耗时较长的奇异值分解.y的显式解为：

(5)

其中，UK+1∈m×r，VK+1∈n×r通过

(6)

得到.从上面的步骤可以看出，每次迭代至少需要求解两次SVD，而该过程是最耗时的.要想有效地减少算法的运行时间，减少迭代次数是最直接的解决方案.

(7)

在y迭代之后完成对Z的第二次更新.

(8)

通过上述改变，线性约束乘数在一次迭代中完成了以前两次迭代的工作，而线性约束乘数又是收敛的关键指标，它更新速度变快，算法的收敛速度也将比以前要快.同时迭代次数的减少也使得SVD次数减少，这是整个算法运行时间缩短的关键.

3 新的均衡参数和停机准则

在实验过程中作者发现，有时在迭代的末尾阶段，稀疏矩阵x变化很小，但却要耗费大量的迭代次数，这使得算法的效率大打折扣，所以本文引入一个新的停机准则来解决这个问题.而原ADM分解精度不高，主要是由于在迭代分解的过程中没有考虑矩阵x和y的权重.针对这一问题，本文将规整化参数δ这一权重参数引入到迭代过程中.而新的均衡参数的加入将会对求解过程的收敛性造成影响，文献[9]中已经针对变分不等式问题加入新的均衡参数后的收敛性做了证明，但本文基于RPCA的运动目标提取是凸规划问题，所以需要重新证明.本文的主要思路是通过证明变分不等式所求的解也是凸规划问题的一个最优解，得到在加入新的均衡参数的前提下，依然可以求得式(1)的解，即新加入的均衡参数对原最优问题的收敛性没有影响.

3.1 收敛性证明

设(x*，y*，Z*)是式(3)的一个鞍点，对于任意的(x，y，Z)∈U有[15]：

L(x*，y*，Z)≤L(x*，y*，Z*)≤L(x，y，Z*)

(9)

令∂θ1(x)和∂θ2(y)分别是凸函数θ1(x)和θ2(y)的次微分算子.f(x)∈∂θ1(x)和g(y)∈∂θ2(y)分别是θ1(x)和θ2(y)的一个次梯度.则求式(3)的一个鞍点等价于：

求u*=(x*，y*，Z*)∈U，f(x*)∈∂θ1(x*)和g(y*)∈∂θ2(y*)，使得

(10)

式(10)可以看作是式(2)的一阶最优条件.为了将式(10)紧凑化，现做如下替换：

对于u=(x，y，Z)∈U，f(x)∈∂θ1(x)和g(y)∈∂θ2(y)，记

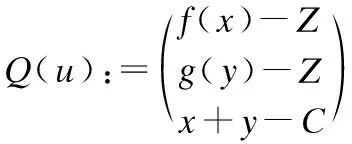
(11)

所以，式(10)等价于：

求u*=(x*，y*，Z*)∈U，f(x*)∈∂θ1(x*)和g(y*)∈∂θ2(y*)使得

(u-u*)TQ(u*)≥0，∀u∈U

(12)

(13)

由此可得，在条件相同的前提下，满足变分不等式问题的解也是凸规划问题的一个鞍点.因此，文献[9]的NADM中的新的均衡参数也可以运用到式(2)求解中.

3.2 改进原理与算法流程

针对迭代末尾阶段效率低的问题，本算法加入了一个误差参数

ey(yk+1，β)=yk+1-Py[yk+1-β(g(yk+1)-Zk+1)]

(14)

作为额外的停机准则，其中Py[.]表示从n到y的投影，yk+1是迭代k+1次后的y值.该参数反映的是每一次迭代后背景矩阵y的变化情况.之所以不直接用yk+1-yk，是由于一般来说背景相对变化较小，并不能真实反映每次迭代后的变化情况，所以有可能造成停机准则的误判，而改进的误差参数ey(yk+1，β)将稀疏矩阵x的变化通过Zk+1和y联系到一起，避免了以y为唯一依据而引起的误判.改进后的停机准则在每次迭代结束后会进行一次判断，当误差小到一定的范围时，就会触发该停机准则，从而避免后面不必要的迭代过程，提高整个算法的计算效率.

针对原ADM提取目标精度不高的问题，本文通过新的均衡参数γ=2e-δ∈(0，2)，将式(1)中的规整化参数δ加入到线性约束乘数Z中.而δ起着调节x和y权重的作用，这让每次迭代中x和y的分配根据权重进行了优化，从而使最后的提取精度能得到提高.加入均衡参数后，SADM中对约束乘数的两次更新分别为：

(15)

(16)

SADM在改变了原ADM迭代策略的基础上，还引入了一个新的均衡参数和停机准则，这些改进使得算法的耗时减少，同时提取精度也得到了提高.算法流程为：

输入：图片序列组成的矩阵C

输出：输出x和y矩阵

1)初始化x，y，Z，令

γ∈(0，2)，β∈(0，1)，ε>0

2)更新包含运动目标的稀疏矩阵x

xk+1=argminxLβ(xk，yk；Zk)

3)对约束乘数Z第一次更新

4)更新包含背景的低秩矩阵y

5)对约束乘数Z第二次更新

6)计算停机准则ey

ey(yk+1，β) =yk+1-Py[yk+1-β(g(yk+1)-Zk+1)]

7)若矩阵x和y中变化率较大的都小于设定的临界值max{‖xk+1-xk‖，‖ey(yk+1，β)‖}≤ε则算法结束，否则进行下一轮迭代.

4 实验对比与分析

为了对上述改进的有效性进行验证，实验在提取精度、运行时间和迭代次数三方面与其它方法进行对比.实验选取了广泛使用的Wallflower[17]中的MovedObject(MO)，WavingTrees(WT)，TimeOfDay(TD)，Camouflage(C)，LightSwitch(LS)五个图片数据集作为测试数据.该数据集是微软研究员John Krumm等参与制作的，由于其包含的丰富场景对检测提取算法的潜在问题具有很好的效果，所以该数据集在前背景提取实验中广泛采用，具有较高的权威性.

图2 实验效果对比Fig.2 Comparison of experimental result

实验时分别从每个图片数据集中取100张连续图片P1,P2,P3…P100作为输入数据，组成输入矩C=matrix{P1,P2,P3…P100}阵.实验选取EALM[7]、IALM[7]、MoG-RPCA[18]、FPCP[19]、R2PCP[20]和LSADM[10]算法进行对比实验，同时对比中还加入了去掉均衡参数的试验结果，以验证均衡参数对提取精度的影响.

本文的实验平台是配置了Windows 7系统，CPU Intel(R)Core(TM) i7-4790 3.60GHz，内存8GB Dell台式机，程序均用Matlab R2014b编程实现.

4.1 提取效果对比

在提取效果对比试验中，本文选取了C 的第251帧，MO的第698帧，WT的第251帧，TD的第1850帧以及LS的第1865帧进行实验效果展示，并分别将分解出的稀疏矩阵x进行二值化，对比效果如图2所示.从图2和不同方法的对比中可以看出，SADM都有很好的提取效果；对于五个不同的图片数据集，SADM的提取效果也比较稳定.

同时为了验证均衡参数对提取精度的影响，本文将去掉均衡参数后的提取效果和SADM提取效果进行对比，结果如图3所示.

图3 均衡参数实验效果对比Fig.3 Comparison of experimental results about equalizing parameter

通过对比结果可以发现，去掉均衡参数后，提取的目标中有更多噪声或目标提取的不完全，这说明算法在分低秩和稀疏矩阵的分解上受到影响，使得运动目标的提取精度降低，这也验证了均衡参数对提取精度的改善作用.

4.2 提取精度对比

为了对提取精度进行量化比较，本文采用Maddalena等[21]用到的F测度对结果进行量化，其计算公式为：

其中，

TP即为True Positive，FN为False Negative，FP为False Positive.本文中TP代表本来属于运动目标，检测结果也为运动目标的点；FN和FP依次类推.F测度对比柱状图如图4所示，数据如表1所示.

图4 F测度对比图Fig.4 Comparison on F measure

从F测度对比结果来看，测试数据中SADM的效果基本都是最好的，而且整体效果相对其它方法有了很大的改进，从最后一行的均值可以发现，本文算法的平均值在对比的8种算法中是最高的，平均提高了33.04%.从F测度对比图可以发现，SADM的F测度变化相对较小，说明它的鲁棒性相比其它方法更好.

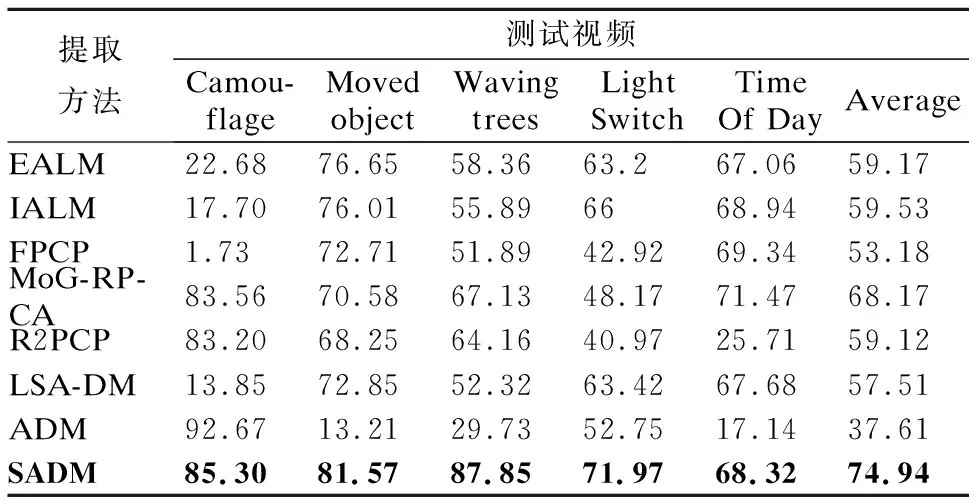
表1 F测度对比Table 1 Comparison on F measure

有无均衡参数的量化对比结果如表2所示.从表中可以看出，三个测试数据集的提取精度都是加入均衡参数的高，对比提取精度的均值会发现，加上均衡参数后比去掉的精度提高了11.91%.

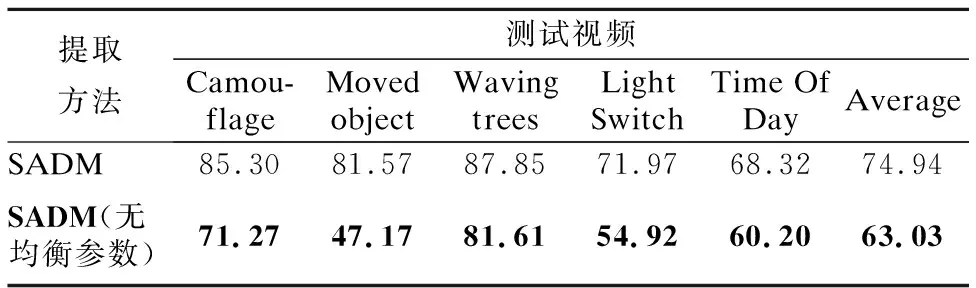
表2 均衡参数结果量化对比Table 2 Comparison of precision quantification about equalizing parameter

4.3 运行时间对比

算法的运行时间对比数据如表3所示.从表中可以看出，相比原ADM算法，SADM运行时间平均缩短了98.8%.

在前文提到，收敛次数与运行时间有一定的关系，随着收敛次数的减少，算法中最耗时的SVD过程也相应减少，从而使运行时间缩短.为了验证这一点，实验检测了各个算法的迭代次数，数据如表4所示.从表3和表4的实验结果可以看出，迭代次数较短的算法，其运行时间相对来说也比较短.SADM算法由于采用了新的迭代策略和停机准则，使算法的收敛速度加快，表3较短的运行时间和表4中SADM相对较少的收敛次数也验证了这一点.

表3 运行时间对比(单位：秒)Table 3 Comparison on running time

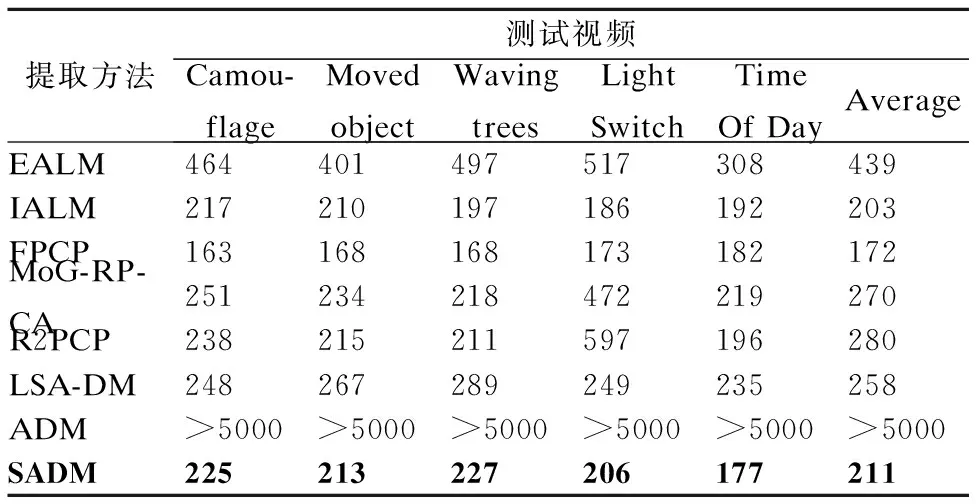
表4 迭代次数对比Table 4 Comparison on iteration times

从这些对比实验中可以发现，本文的运行时间和迭代次数相对于原ADM都有了很大提升，但在运行时间上，本文算法平均约32s不是最好的，这主要是因为SADM中加入了新的均衡参数，为了提高提取精度而牺牲了一定的运行时间.从表1和表3的实验结果可以看出，运行时间较短的算法，其F测度相对来说比较低，这是因为如果时间过短，就会造成分解结果相对较差，反映在实验结果上就是F测度比较低.而本文的方法在保证较短运行时间的同时，F测度也很高，对二者进行了一个很好的均衡.

5 结 语

本文提出了一种基于对称交替方向鲁棒主成分分析的运动目标提取算法，该方法在原ADM基础上，通过改进算法的迭代方式和加入新的停机准则，使算法耗时减少，算法耗时相对原ADM提高了98.8%，同时通过加入新的均衡参数，使运动目标的提取精度平均提高了33.04%.但该方法在耗时方面还有提升空间，未来可在奇异值分解方法等方面继续进行优化.

：

[1] Cao X，Yang L，Guo X.Total variation regularized RPCA for irregularly moving object detection under dynamic background[J].IEEE Transactions on Cybernetics，2015，46(4)：1014-1027.

[2] Fang Shuai，Qu Cheng-jia，Yang Xue-zhi，et al.Linear prediction band selection based on optimal combination factors[J].Journal of Image and Graphics，2016，21(2)：255-262.

[3] Cai Nian，Zhou Yang，Liu Gen，et al.A survey：robust principal component analysis methods for moving object detection[J].Journal of Image and Graphics，2016，21(10) ：1265-1275.

[4] Candes E，Li X，Ma Y，et al.Robust principal component analysis[J].International Journal of ACM，2011，58(3)：1-73.

[5] Wright J，Peng Y，Ma Y，et al.Robust principal component analysis：exact recovery of corrupted low-rank matrices by convex optimization[J].Conference and Workshop on Neural Information Processing Systems，2009：2080-2088.

[6] Lin Z，Ganesh A，Wright J，et al.Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix[J].Journal of the Marine Biological Association of the UK，2009，56(3)：707-722.

[7] Lin Z，Liu R，Su Z，et al.Linearized alternating direction method with adaptive penalty for low-rank representation[J].Conference and Workshop on Neural Information Processing Systems，2011：612-620.

[8] Yuan X，Yang J.Sparse and low-rank matrix decomposition via alternating direction methods[J].Pacific Journal of Optimization，2013，9(1)：167-180.

[9] Zhang Min，Han De-ren，He Hong-jin，et al.A new alternating direction method for solving separable variational inequality problems[J].Scientia Sinica Mathematica，2012，42(2)：133-149.

[10] Glowinski R，Le Tallec P.Augmented lagrangian and operator-splitting methods in nonlinear mechanics[M].Society for Industrial and Applied Mathematics，Philadelphia，1989.

[11] Goldfarb D，Ma S，Scheinberg K.Fast alternating linearization methods for minimizing the sum of two convex function[J].Mathematical Programming，2009，141(1-2)：349-382.

[12] Ma S.Algorithms for sparse and low-rank optimization：convergence，complexity and applications[M].Thesis，2011.

[13] Douglas J，Rachford H H.On the numerical solution of heat conduction problem in 2 and 3 space variables[J].Transactions of the American Mathematical Society，1952，82(2)：421-439.

[14] Peaceman D H，Rachford H H.The numerical solution of parabolic elliptic differential equations[J].SIAM Journal on Applied Mathematics，2006，3(1)：28-41.

[15] M H Xu，T Wu.A class of linearized proximal alternating direction methods[J].Journal of Optimization Theory and Applications，2011，151(2)：321-337.

[16] Facchinei F，Pang J S.Finite-dimensional variational inequalities and complementarity problems[M].Berlin：Operations Research,Springer，2003.

[17] Toyama K，Krumm J，Brumitt B，et al.Wallflower：principles and practice of background maintenance[J].IEEE International Conference on Computer Vision，1999，1(1)：255-261.

[18] Zhao Q，Meng D，Xu Z，et al.Robust principal component analysis with complex noise[J].International Conference on Machine Learning，2014：55-63.

[19] Rodriguez P，Wohlberg B.Fast principal component pursuit via alternating minimization[J].IEEE International Conference on Image Processing，2014：69-73.

[20] Hintermüller M，Wu T.Robust principal component pursuit via inexact alternating minimization on matrix manifolds[J].Journal of Mathematical Imaging and Vision，2014，51(3)：361-377.

[21] Maddalena L，Petrosino A.A fuzzy spatial coherence-based approach to background foreground separation for moving object detection[J].Neural Computing and Applications，2010，19(2)：179-186.

附中文参考文献：

[2] 方 帅，瞿成佳，杨学志，等.组合因子最优的线性预测波段选择[J].中国图象图形学报，2016，21(2)：255-262.

[3] 蔡 念，周 杨，刘 根，等.鲁棒主成分分析的运动目标检测综述[J].中国图象图形学报，2016，21(10)：1265-1275.

[9] 张 敏，韩德仁，何洪津，等.解可分离结构变分不等式的一种新的交替方向法[J].中国科学：数学，2012，42(2)：133-149.