多种沉默型P2P蠕虫共同传播的建模与分析
周翰逊,王鹏祥,任佃武,郭 薇,李晓光
1(辽宁大学 信息学院,沈阳 110036)
2(沈阳航空航天大学 计算机学院,沈阳 100136)
1 引 言
互联网的不断发展逐渐改变了人们的生活习惯,尤其是P2P软件可以让人们在上网的同时更好的分享网络信息和资源[1].但由于许多P2P软件存在安全漏洞,若被不法用户编制的P2P蠕虫所利用而感染,那么整个P2P网络有陷入瘫痪的可能.
由于网络蠕虫的传播模型可以揭示其传播本质,人们对于P2P蠕虫的传播模型进行了深入的研究.文献[2]研究了主动扫描攻击的P2P蠕虫模型.文献[3]则基于三元矩阵对于主动的P2P蠕虫进行了建模.冯朝胜等人[4-6]分别对于被动型,沉默型以及激发型P2P蠕虫进行了数学建模,并且通过仿真实验对于模型进行了验证.
此外,随着计算机软硬件性能提升,多种P2P软件会在同一主机上运行,那么多种P2P蠕虫就会在网络中同时传播.故本文提出了多种沉默型P2P蠕虫共同传播的数学模型.
2 模型结构
2.1 沉默型P2P蠕虫共同传播过程
沉默型P2P蠕虫通过软件漏洞运行的P2P蠕虫对主机上的连接进行监听,并开始新的传播和感染.而多种沉默型P2P蠕虫共同传播是指同一时间有多种不同的沉默型P2P蠕虫利用正常连接和P2P软件漏洞对未被沉默型P2P蠕虫感染的用户主机进行监听并且传播,进而对用户主机进行感染.
在多种沉默型P2P蠕虫共同传播的过程中,由于P2P蠕虫的感染率对接触率有很大影响,令
pd+pu=(pd1+pu1+…+pdn+pun)/n
(1)
其中,pd+pu表示P2P蠕虫下载和上传时主机被感染的概率和的平均数,n表示蠕虫的种类.蠕虫传播模型将接触率β(t)定义如下:
β(t)=β0[(1-I(t)/N)η+(1-I(t)(pd+pu)/N)η]
(2)
其中β0为接触率的初始值,η是感染主机数量的变化对接触率的敏感度.(1-I(t)/N)η表示感染主机数量的不断增大,网络拥塞程度会制约蠕虫的传播.
2.2 主机转换状态
将P2P蠕虫感染过程中的主机划分为三类:易感类,感染类和恢复类.单位时间内,网络中的主机只能处于易感类,感染类或恢复类这三种状态中的一种. 主机的转换状态分为四种情况:直线型,直角型,渐进型和瀑布型,如图1所示.其中,直线型、直角型和渐进型是多种沉默型P2P蠕虫的不共存情况;瀑布型是多种沉默型P2P蠕虫的共存情况.

表1 模型参数Table 1 Parameters of the model
直线型主机间的状态转换如图1(a)所示,具体转化过程如下:
1. S→I1(t)…Ik(t)…In-1(t)是指易感主机被蠕虫k(1≤k≤n-1)感染后转化为感染主机.
2. S→In(t)是指易感主机被蠕虫n感染后转化为感染主机.
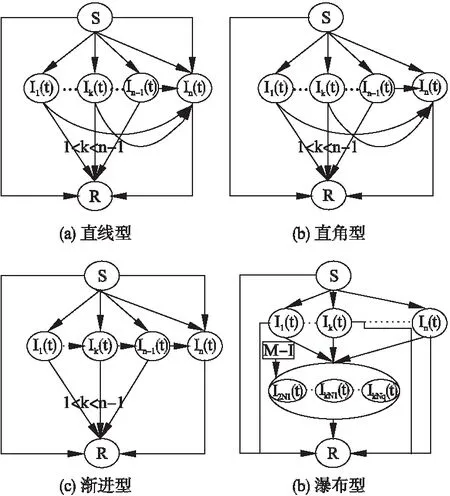
图1 各类主机的状态转换图Fig.1 State transition graph of different types of hosts
3. I1(t)…Ik(t)…In-1(t)→In(t)是指蠕虫k(1≤k≤n-1)被蠕虫n抢占的主机.
4. I1(t)…Ik(t)…In-1(t)→R,S→R,In(t)→R三个状态转换过程,是相应的主机由于安全软件的防护使主机具有免疫能力,即转化为恢复主机.
图1(b)中主机间的直角型状态转换图与直线型状态转换图的不同之处是易感主机不能被蠕虫n所感染.图1(c)中的渐进型状态转换图与直线型状态转换图中的不同之处是Ik(t)→Ik+1(t)表示蠕虫k(1≤k≤n-1)只能被蠕虫k+1抢占.图1(d)中的瀑布型状态转换图为多种沉默型P2P蠕虫共存状态图,表示从蠕虫1…蠕虫k(2≤k≤n-1)…蠕虫n(n>k)任意两种或多种沉默型P2P蠕虫同时共存于同一台感染主机上.
2.3 多种沉默型P2P蠕虫共同传播数学模型
2.3.1 多种沉默型P2P蠕虫共同传播的不共存模型
易感主机转化为感染主机的情况有两种:文件的上传和下载.由图1(a)中直线型状态转换图可知,易感主机被蠕虫1感染的变化率为:
dS1(t)/dt=μN-β(t)S(t)Pd1I1(t)/N-S(t)Pu1[1-[1-1/N]β(t)I1(t)]-λmS(t)-μS(t)
(3)
被蠕虫2…蠕虫k(2≤k≤n-1)…蠕虫n-1(n>2)感染的易感主机的变化与(3)类似,因此不再赘述.
被蠕虫1感染的主机变化率如下所示:
dI1(t)/dt=β(t)S(t)I1(t)Pd1/N+S(t)Pu1[1-[1-1/N]β(t)I1(t)]-β(t)I1(t)PdnIn(t)/N-I1(t)Pun[1-[1-1/N]β(t)In(t)]-λmI1(t)-μI1(t)
(4)
含有蠕虫2…蠕虫k(2≤k≤n-1)…蠕虫n-1(n>2)的感染主机转化为被蠕虫n感染的主机数量变化 (4)类似,因此不再赘述.
恢复主机的变化率如下所示:
dR(t)/dt=λmS(t)+λmI(t)-μR(t)
(5)
由此可以得到直线型传播模型为:
dR(t)/dt=λmS(t)+λmI(t)-μR(t)
N=S(t)+I(t)+R(t)
(6)
同理,可以得到直角型传播模型为
[1-1/N]β(t)Ii(t)])-λmI(t)-uI(t)
dR(t)/dt=λmS(t)+λmI(t)-μR(t)
N=S(t)+I(t)+R(t)
(7)
渐进型传播模型与直线型传播模型一样,此处不再赘述.
2.3.2 蠕虫共同传播的共存模型
易感主机被蠕虫2…蠕虫k(2≤k≤n-1)…蠕虫n(n>k)感染的变化率与含有k(k>=2)种蠕虫的主机转化蠕虫感染的主机的情况与(8)类似,故不再赘述.推导过程同不共存类似,这里不再列出.
从上文可知导致易感主机转化为感染主机的原因主要有两种:文件的上传和下载.由图1(d)可以得到被蠕虫1感染的易感主机和感染蠕虫1的主机数量的变化率如下所示,即瀑布型传播模型:
dR(t)/dt=λmS(t)+λmI(t)-μR(t)
N=S(t)+I(t)+R(t)
(8)
3 蠕虫不泛滥的条件及证明
P2P蠕虫的传播速率对蠕虫不泛滥条件有很大的影响,下文将证明多种沉默型P2P蠕虫传播模型的不泛滥条件令:
pId+pIu=max{pd1+pu1,…,pdn+pun}
(9)
定理1.根据直线型传播模型,多种沉默型P2P蠕虫不会泛滥的条件是

(10)

直线型传播模型中,
<β(t)I(t)(pId+pIu)-λmI(t)-μI(t)<0
(11)
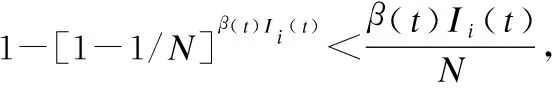
同理,根据直角型传播模型、渐进型传播模型可证、瀑布型传播模型、分别可以得出不泛滥的条件的公式为(12),(13),(14)所示:
(12)
(13)
(14)
4 平衡点的稳定性分析
蠕虫的传播速率越快则传播模型趋向于稳定时感染的主机数量就越多,下文将证明多种沉默型P2P蠕虫传播模型的无病平衡点和地方性平衡点,令pId+pIu和pSd+pSu如公式(15):
pId+pIu=max{pd1+pu1,…,pdn+pun}
pSd+pSu=min{pd1+pu1,…,pdn+pun}
(15)
4.1 无病平衡点和地方病平衡点
4.1.1 多种沉默型P2P蠕虫共同传播的不共存模型
根据直线型传播模型可知,如果模型是稳定的,则必须满足以下条件:
(16)
当I(t)=0时,I1(t)=I2(t)=…=In-1(t)=0
此时得到无病平衡点:
(17)
当I(t)>0时,此时得到地方病平衡点:
(18)
同理,根据直角型传播模型可求出无病平衡点为:
(19)
地方病平衡点为:
(20)
由于渐进型传播模型与直线型传播模型类似,此处不再赘述.
4.1.2 蠕虫共同传播的共存模型
根据瀑布型传播模型可求出无病平衡点为
(21)
地方病平衡点为:
(22)
4.2 平衡点的稳定性分析与证明
4.2.1 无病平衡点的稳定性
当直线型传播模型趋向于稳定时,得到该模型在无病平衡点处的雅克比(Jacobian)矩阵F(Qt11) :
(23)
由公式(23),解得F(Qt11)的特征值,如下所示:
(24)
由于直线型传播模型所有的参数全部为正值,因此λ1<0,λ3<0.若模型在无病平衡点处是局部渐进稳定的,那么λ2<0,即
(25)
令基本再生数为G0
(26)
根据直线型传播模型在无病平衡点处的稳定性,可以得到以下引理:
引理1.若G0<1,则在无病平衡点Qt11处直线型传播模型是局部渐进稳定的;
证明:由稳定性定理知,渐进稳定的充分条件是其Jacobian矩阵的特征值λj<0,j=1,2,3由公式(24)可知,λ1<0,λ3<0,如果令λ2<0,即
得到G0<1,满足引理中的充分条件.证毕
同理,根据直角型传播模型,渐进型传播模型,瀑布型传播模型分别可证在无病平衡点Qt21,Qt11Qt31均为局部渐进稳定的;
定理2.若G0≤1,则在无病平衡点Qt11处直线型传播模型是全局渐进稳定的.
证明:由直线型传播模型可知,
S′(t)≤μN-λmS(t)-μS(t)
构造Lyapunov函数U(t)=I(t):
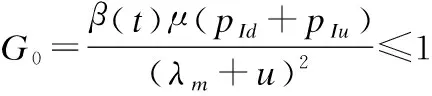
得到在无病平衡点Qt11处是全局渐进稳定的.
同理,根据直线型传播模型,渐进型传播模型,瀑布型传播模型得出,在无病平衡点Qt21,Qt11,Qt31处是全局渐进稳定的.
4.2.2 地方病平衡点的稳定性
地方病平衡点的Jacobian矩阵:
F(Qt12)=
(27)
解得,矩阵F(Qt12)的特征值满足:
f(λ)=a0λ3+a1λ2+a2λ+a3
(28)
其中,
(29)
令基本再生数G1为
(30)
根据地方病平衡点处的稳定性,可得以下引理.
引理2.若G1>1,则在地方病平衡点Qt12处直线型传播模型是局部渐进稳定的.
证明:地方病平衡点Qt12的Routh-Hurwitz矩阵如下所示:
(31)
若(a1a2-a0a3)/a1与a1都为正值,那么3个特征值均为负实数,则Routh-Hurwitz稳定时的充分必要条件就满足.由于G1>1,可得(a1a2-a0a3)/a1>0.故在地方病平衡点Qt12处是局部渐进稳定的.

定理3.若G1≥1,则在地方病平衡点点Qt12处直线型传播模型是全局渐进稳定的.
证明:根据直线型传播模型,构造Lyapunov函数U(t)
(32)
可得,在地方病平衡点Qt12处直线型传播模型是全局渐进稳定的.
5 仿真验证及分析
在不共存的条件下验证了四种沉默型P2P蠕虫的共同传播的实验结果;图像的横轴为时间轴,纵轴代表主机数目.
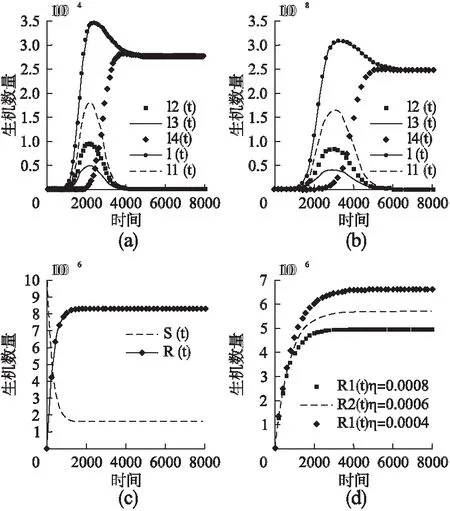
图2 不共存条件下四种沉默型P2P蠕虫共同传播实验结果Fig.2 Result of four types of multi-reactive-P2P-worms spreading together in the non-coexistence situation
图2是直线型传播模型中接触率、敏感度和感染率对易感主机、感染主机以及恢复主机数目影响的仿真结果,以及无病平衡点和地方病平衡点的验证结果.其中,S(t)、I(t)、R(t)的初值分别为9999980、20、0.I1(t)、I2(t)、I3(t)、I4(t)的初值分别为5、5、5、5.η、λm的初值分别为0.0006、0.0008.
图2中(a)、(b)是接触率β(t)的变化对易感主机和感染主机的影响,由图(a)、(b)可以看出,β0的值越大,趋于稳定时,被感染的主机数量也越多.
图2(a)中也反映了当趋向于平衡且I(t)>0时,地方病平衡点的仿真结果.图2(a)描述了I(t)、I1(t)、I2(t)、I3(t)以及I4(t)的变化情况.将趋向于稳定时的实验数据代入公式(18),可得I(t)的取值范围为2.43×106~3.12×106,实验数据为Ib(t)=2.4723×106,由于Ib(t)在I(t)的取值范围内,所以图2(a)中的实验数据与直线型传播模型达到平衡点的数据吻合.
图2中的(c)表示趋向于平衡且I(t)=0时,S(t)和R(t)的变化情况,将趋向于平衡时的数据代入公式(17)可得,S(t)的值为1/6×107,R(t)的值为5/6×107,实验得到S(t)=0.166667×107,R(t)=0.833333×107.可知达到无病平衡点时S(t)、R(t)的值与无病平衡点处的仿真实验结果是相互吻合的.
图2 (d)是敏感度η对恢复率的影响,η的值越大,当趋于稳定时,恢复的主机数量就越少.所以由图2(d)可知,当趋向于稳定时R1(t) 直角型和渐进型状态转换仿真结果同上述结果类似.共存的实验结果亦同推导结果相同,故在此不再展开论述. 本文提出了多种沉默型P2P蠕虫共同传播的数学模型,并将传播模型分为共存时的瀑布型和不共存时的直线型、直角型和渐进型.并讨论了四种传播模型中的不泛滥条件,推导出了多种沉默型P2P蠕虫传播过程中的平衡点,并讨论了传播模型平衡时的稳定性.通过仿真实验验证了传播模型不泛滥条件以及趋于稳定时平衡点的正确性,并且讨论了接触率、感染率以及敏感度对于模型的影响. : [1] Guan Lei,VIP-P2P technology Secret-P2P network technology principles and typical system development.[M].Beijing:Tsinghua University Press,2011. [2] Tao Lia,Guana Zhi-hong,Xianyong Wua.Modeling and analyzing the spread of active worms based on P2P systems[C].Computers & Security,2007:213-218. [3] Chen Ting,Zhang Xiao-song,Li Hong-yuan,et al.Propagation modeling of active P2P worms based on ternary matrix[J].Journal of Network and Computer Applications,2013,36(5):1387-1394. [4] Feng Chao-sheng,Qin Zhi-guang,Yuan Ding,et al.Modeling propagation and immunization of passive worms in peer to peer networks[J].Journal of University of Electronic Science and Technology of China,2013,41(5):884-889. [5] Feng Chao-sheng,Qin Zhi-guang.Laurence cuthbert and laurissa tokarchuk,reactive worms propagation modeling and analysis in Peer-to-Peer networks[J].Journal of Computer Research and Development,2010,47 (3):500- 507. [6] Feng Chao-sheng,Yuan Ding,Qing Yu,et al.Dynamic modeling of reactive worm propagation in P2P networks[J].Acta,Electronica,Sinica,2012,40(2):300-307. 附中文参考文献: [1] 管 磊.VIP-P2P技术揭秘—P2P网络技术原理与典型系统开发[M].北京:清华大学出版社,2011. [4] 冯朝胜,秦志光,袁 丁,等.P2P网络中被动型蠕虫传播与免疫建模[J].电子学报,2013,41(5):884-889. [5] 冯朝胜,秦志光,劳伦斯·库珀特,等.P2P网络中沉默型蠕虫传播建模与分析[J].计算机研究与发展,2010,47(3):500-507. [6] 冯朝胜,袁 丁,卿 昱,等.P2P网络中激发型蠕虫传播动态建模[J].电子学报,2012,40(2):300-307.6 结 论

