递归替换寻优策略的分解多目标进化算法
王丽萍,丰美玲,邱飞岳,章鸣雷
1(浙江工业大学 经贸管理学院,杭州 310023)
2(浙江工业大学 信息智能与决策优化研究所,杭州 310023)
3(浙江工业大学 现代教育技术研究所,杭州 310023)
1 引 言
在科学研究和实际应用中存在多个目标优化问题,称之为多目标优化问题MOPs(Multi-objective Optimization Problems).多目标优化问题中目标函数之间一般是相互冲突的,没有一个最优解能同时优化所有目标[1-3].由于进化算法一次运行能提供多个Pareto最优解,且不受目标函数数学性质的影响,因此利用进化算法求解多目标优化问题成为近年来的研究热点[4,5].
基于Pareto支配的多目标进化算法(如NSGA-II[6],SPEA2[7])是被最早提出的算法.这些算法在解决两个或三个目标的问题上表现出较好的性能.然而,随着目标数目的增加,算法的搜索能力呈明显下降趋势.主要原因是种群中非支配解的比例急剧增长,导致对种群的选择压力不足,使得种群进化速度减慢,甚至过早停滞.
为增强种群朝Pareto前沿进化,Zhang et al[8]于2007年提出了基于分解的多目标进化算法MOEA/D (Multi-objective evolutionary algorithms based on decomposition).MOEA/D算法的基本思想是,将MOPs中的多个目标按一定的权重分解成若干个单目标子问题,然后进行并行优化,使子问题的解逐渐逼近真实的Pareto前沿.这种机制有效的原因是每个子问题的最优解实际上对应着给定MOP的Pareto最优解.这些最优解的集合可以看作是真实Pareto前沿面一个良好的近似.
为提高算法性能,Zhang et al[9]在2009年提出将差分算子DE引入到MOEA/D中,有效提高算法的收敛速度,增强解决复杂PS(Pareto Set)问题的能力,但该算法的新解替换掉所有较差的解,未考虑替换次数,这导致种群中个体的副本过多,使得算法的多样性明显下降.Qi et al[10]在2014年通过对原始Tchebycheff聚合函数做几何分析,提出了一种新的权向量初始化方法MOEA/D-AWA(MOEA/D with Adaptive Weight Vector Adjustment),该算法根据复杂Pareto前沿周期性调整权值,使子问题的权重向量能够自适应地重新分布,提高解分布的均匀性,然而使用的周期性参数的不同会影响解的性质,并且该算法在替换时未考虑替换次数,一定程度上延缓了收敛速度.Li et al[11]于2014年提出一种稳态匹配模型来协调MOEA/D中解与子问题相互选择,称为MOEA/D-STM(Stable Matching-Based Selection in Evolutionary Multi-objective Optimization),该方法把子问题和解看作是两个不同的代理,子问题倾向于选择那些使其能获得最小聚合函数值的解,而解倾向于选择那些与其距离最近的子问题.该算法的目的是实现多样性和收敛性的平衡,但在选择过程中折中越多,越容易使得解与合适的子问题偏离程度大,并且该算法在新解替换旧解时,仍未考虑替换次数,导致算法整体性能明显下降.同年,Wang et al[12]提出使用全局替换策略的MOEA/D-GR(A Replacement Strategy for Balancing Convergence and Diversity in MOEA/D)算法,新解与能够取得最小聚合函数值的子问题相结合,然后选择与该子问题距离最近的若干个子问题作为替换邻域.MOEA/D-GR算法旨在为新解找到一个最合适的子问题,但一味强调收敛性导致新解在邻域内出现多个副本,牺牲了算法的多样性.Yuan et al[13]于2015年提出根据新解到相关子问题的垂直距离确定替换邻域的MOEA/D-DU算法(Balancing Convergence and Diversity in Decomposition-Based Many-Objective Optimizers),该策略有效提高算法的多样性,但一味强调多样性而忽略算法的收敛性,使得算法的收敛性明显下降.2016年,Zhou et al[14]针对不同的子问题,提出一种新的动态分配计算资源策略MOEA/D-GRA(A Generalized Resource Allocation Strategy for Decomposition-based MOEAs),该策略同样一味强调算法的收敛性却忽略算法的多样性.
为维持多样性的同时提高算法的收敛性,本文根据新解到对应方向向量的垂直距离确定替换邻域,继而提出递归替换寻优策略.该策略主要思想是,在替换邻域内,新解根据聚合函数值大小替换旧解,被替换掉的旧解不被立刻丢弃,而是将旧解重新视为“新解”,在剩下的替换邻域内递归查找是否存在比该解更差的解.若存在,则替换之,将被替换掉的旧解又重新视为“新解”,如此循环,直到当前替换邻域内不存在能够被旧解所替换的解.递归替换寻优策略尽可能避免保留较差解,丢弃较优解,保证最终被丢弃的旧解是当前替换邻域内最差的解.根据垂直距离确定替换邻域,有效保证算法的多样性,在此基础上提出递归替换寻优策略,在维持多样性的同时提高算法的收敛性.
2 背景知识
2.1 分解机制
分解机制是将MOP分解为一系列的子问题,然后利用单目标进化算法求解每个子问题[15].在MOEA/D中,加权和法、切比雪夫法和基于惩罚的边界交叉法是最常用的分解方法[16,17].本文采用的分解方法是切比雪夫函数的改进版本.设λ1,λ2,…,λN是当前子问题的权重向量,Z*是理想点,Z*=min{fi(x)|x∈X}对于任意的i∈{1,2,…,m},λi≥0该函数定义为
(1)
改进版本的切比雪夫函数有以下两个优点.第一,在目标空间中,均匀分布的权重向量可以产生均匀分布的搜索方向;第二,每个权重向量唯一对应于Pareto前沿面上的一个Pareto最优解.这两个优点在一定程度上提高了算法的多样性.
2.2 权重向量产生方法
在MOEA/D中,子问题对应的权重向量分布的均匀性,在一定程度上反映了算法所求得的Pareto解的均匀性.因此,权重向量能否均匀地分布在整个取值空间对于MOEA/D所求得解的质量至关重要.为此,本文选取MOEA/D中原始的权重向量生成方法.
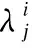
(2)
2.3 MOEA/D算法流程
输入:
①MOP问题;
②停止准则;
③N:MOEA/D分解的子问题个数;
④λ1,λ2,…,λN:均匀分布的N个权重向量;
⑤T:每一个邻域内的权重向量个数.
输出:PF:{F(x1),F(x2),…,F(xN)}.
Step1.初始化:
Step1.1.计算任意两个权重向量之间的欧式距离,为每个权重向量选出最近的T个向量作为其邻域.设B(i)={i1,i2,…,iT},i=1,2,…,N,其中λi1,λi2,…,λiT为距离λi最近的T个权重向量.
Step1.2.初始化种群x1,x2,…,xN,设FVi=F(xi),i=1,2,…,N.
Step1.3.采用基于问题的特定方法初始化z=(z1,z2,…,zm)T.
Step2.更新:
Fori=1,2,…,N,do
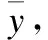
Step2.2.改进:应用问题特定的修正或启发式的改进策略作用于y生成y′.
Step2.3.更新z:若zj>fj(y′),则zj=fj(y′),j=1,2,…,m.
Step2.4.更新邻域解:若gte(y′|λj,z)≤gte(xj|λj,z),j∈B(i),则xj=y′,FVj=F(y′).
Step3.停止判断:若满足停止准则,则算法停止,输出PF,否则返回Step2继续执行.
3 MOEA/D-LR算法
3.1 对比算法缺陷分析及改进策略描述
在原始的MOEA/D中,替换邻域与选择邻域相同,是将与该子问题最接近的若干个子问题作为替换邻域.然而,新解并不一定适合该邻域内的子问题,可能导致接近Pareto前沿的新解被舍弃,不利于引导种群的进化.
MOEA/D-GR算法较好的克服了这个缺陷,其主要思想是,一旦产生一个新解,它就被关联到能获得最小聚合函数值的那个子问题上.然后,与这个子问题最接近的若干个子问题被选择作为该子问题的替换邻域,新解会尝试替换这些子问题的当前解.但是,利用子问题的聚合函数值为一个新解找到一个最合适的子问题有时并非十分合理.当权重向量稀疏分布时,各个权重向量之间距离较远,从而各个子问题的最优值有着很大的差异,这将导致不同聚合函数值之间并不具有可比性.另外,MOEA/D-GR一味强调收敛性,导致新解在邻域内出现多个副本,使得算法的多样性明显下降.
MOEA/D-DU在一定程度上较好的解决了MOEA/D-GR存在的该问题,它采用一个纯几何的观念,利用垂直距离来尽可能地避免那些虽然取得好的聚合函数值,但在目标空间中远离聚合函数所对应的权重向量的解.然而,以上算法都没有考虑到在替换邻域内,被替换掉的旧解可能仍可以替换该邻域内的其他解,即存在比替换掉的解更差的解.
为了克服以上缺陷,本文首先根据新解到对应方向向量的垂直距离确定替换邻域,同时结合递归替换寻优策略,提出改进算法MOEA/D-LR,在维持算法多样性的同时,提高算法的收敛性.
MOEA/D-LR算法及其四个比较算法具体策略描述如下:
如图1(a)所示,在选择邻域B(i)(λ2,λ3,λ4)内任取两个个体进行杂交,产生新解x.对于MOEA/D算法,如图1(b)所示,替换邻域与选择邻域相同也为λ2,λ3,λ4,由于新解x在该邻域内权重向量上的聚合函数值均大于其他个体,故新解x被丢弃.然而新解x明显更接近于真实的Pareto前沿,丢弃x将导致算法的收敛性下降.
对于MOEA/D-GR算法,如图1(c)所示,为新解x找到它最合适的子问题x6,确定替换邻域为λ5,λ6,λ7,新解x优于x5,x6,x7,故x将同时替换x5,x6,x7,这将使得x在该邻域内产生多个副本,导致算法的多样性明显下降,难以促进种群的收敛.
对于MOEA/D-DU算法,如图1(d)所示确定替换邻域为λ6,λ7,λ5,x优于x6,故x将替换x6,x6被丢弃.然而在该邻域内,x6比x5更接近Pareto前沿,这将导致较好的解x6被丢弃,较差的解x5被保留,使得算法的收敛性显著下降.
对于MOEA/D-LR算法,如图1(e)所示,根据新解x到方向向量的垂直距离确定替换邻域为λ6,λ7,λ5,x优于x6,故x将替换x6,被替换掉的解x6不被立刻丢弃,而是视为“新解”,递归查找是否x6能替换邻域内的其他解.重新计算在该邻域内,x6到除λ6以外的权重向量的垂直距离,得到替换邻域为λ5,λ7,x6优于x5,故x6将替换x5,x5没有比邻域内其他解优,即x5是该邻域内最差的解,丢弃x5.由以上分析可得,与MOEA/D相比,MOEA/D-LR在提高多样性的同时提高算法的收敛性;与MOEA/D-GR相比,MOEA/D-LR在维持收敛性的同时提高算法的多样性;与MOEA/D-DU相比,MOEA/D-LR算法在维持多样性的同时其收敛性显著提高.
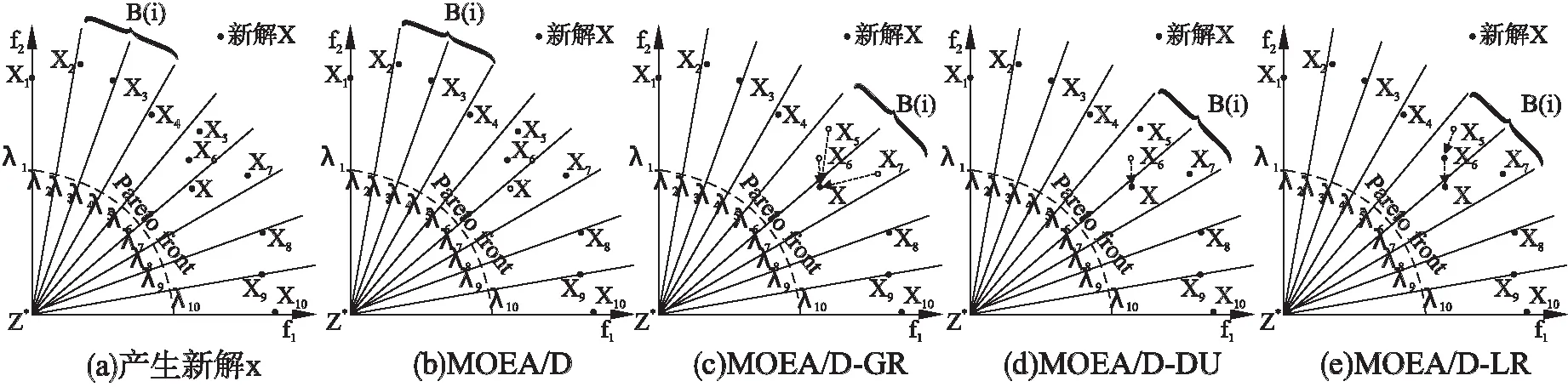
图1 五种算法的解集更新示意图Fig.1 Solution set update of the five algorithms
3.2 算法主要修改部分
3.2.1 替换邻域的确定
在MOEA/D算法流程中,将Step2.4更新邻域解部分使用函数UpdateCurrentPop(y,z*,P,K)代替.
UpdateCurrentPop(y,z*,P,K)
Step2.4.1.j←1toN执行,计算y到每个权重向量λj的垂直距离,记为dj,2(y).
Step2.4.2.从N个距离dj,2(y),j=1,2,…,N中选择最小的K个距离,得到dj1,2(y)dj2,2(y)…djk,2(y).
Step2.4.3.k←1toK执行,若gte(y|λjk,z) Step2.4.4.被替换掉的旧解xjk不被立刻丢弃,而是存储为temp,temp←xjk. 函数UpdateCurrentPop除了返回上述定义的值外,还需返回最小的K个垂直距离所对应的权重向量的编号(即替换邻域B(i))以及被替换掉的旧解xjk的值.在MOEA/D的基础上,根据垂直距离确定替换邻域,并结合递归替换寻优策略,提出了改进算法MOEA/D-LR,将上述算法流程增加如下步骤(加在Step2.4.4后): 3.2.2 递归替换寻优策略 UpdateCurrentPop-LR(y,z*,P,K) Step2.4.5.删除旧解xjk所对应的权重向量,将剩下的权重向量作为新的替换邻域. Step2.4.6.将被替换掉的旧解temp重新视为“新解”(y←temp),在新的替换邻域内递归查找是否 “新解”能够替换其他的解. Step2.4.7.若gte(y|λjk,z) 为验证本文提出的MOEA/D-LR算法的性能,将该算法与原始的MOEA/D算法[8]、MOEA/D-DRA[18]、MOEA/D-GR[12]和MOEA/D-DU[13]进行实验仿真对比.本文选取的测试用例为两目标的WFG系列测试函数WFG1-WFG9和三目标的DTLZ系列测试函数DTLZ1-DTLZ6[19,20]. 为保证算法对比的公平性,本文所有的实验数据都是通过每个算法在每个测试问题上重复独立运行20次获得.本文遗传操作的交叉算子采用SBX算子,交叉分布指数ηc为20,交叉概率Pc为1.0,分布指数ηm设置为20,变异概率Pm为1/n,其中n表示决策变量的个数.所有算法的种群规模N均设置为100,邻域大小T设置为N*0.2.在MOEA/D-DU和MOEA/D-LR中,替换邻域K的设置与选择邻域相同,均为N*0.2.WFG系列测试函数的最大迭代次数Maxgen设置为250,DTLZ2和DTLZ4测试函数的最大迭代次数Maxgen为500,DTLZ1、DTLZ3、DTLZ5、DTLZ6测试函数的最大迭代代数为Maxgen为1000. 为避免单个性能度量指标的片面性,能够更加准确、全面地对该算法进行评价,本文采用IGD[21]、S[22]和HV[23]指标来分析算法的收敛性和分布性.IGD指标能够同时反映出算法收敛性和多样性.IGD指标值越小,表明所求得的近似Pareto前沿越接近整个真实的Pareto前沿,解集的收敛性和分布性整体效果越好.S指标用于评估算法所求得的近似解在目标空间上的均匀性.S指标越小,表明所求得的Pareto解在目标空间上的分布越均匀.HV指标用于衡量多目标进化算法所求得的近似Pareto前沿的分布性和收敛性,HV指标越大,表示算法所求得的解集的整体性能越优. 本文首先使用WFG系列测试函数对提出的MOEA/D-LR算法进行性能测试.表1和表2列出了每个算法在每个测试函数上20次运行的IGD、HV的均值和标准差,表中所有算法在每个函数上的各项最优值被加粗显示.为分析的简便,本文还画出了WFG系列9个测试函数、5种算法所求得的HV指标值的盒图. 4.3.1 IGD指标对比 通过分析表1数据可以得到以下几点结论: 表1 20次运行的IGD的统计结果Table 1 Statistical results of IGD for 30 runs 1)在WFG系列测试函数上,算法MOEA/D-GR所求得的IGD均值与MOEA/D基本相差不大,原因在于MOEA/D-GR仅强调算法的收敛性而忽略了算法的多样性,新解将替换邻域内聚合函数值小的解全部替换,使得新解在对应的邻域内出现多个副本,导致算法的多样性明显下降,难以促进种群的收敛. 2)在测试函数WFG1-WFG9上,可以看出MOEA/D-DU的IGD均值和标准差都比原始的MOEA/D算法小,原因在于MOEA/D-DU算法采用垂直距离确定替换邻域的策略,维持了解的多样性,引导解朝向Pareto前沿进化,防止解陷入局部最优,提高解的性能. 3)比较MOEA/D-LR算法与MOEA/D算法可得,在WFG系列测试函数上,MOEA/D-LR算法无论是IGD均值还是标准差都明显优于MOEA/D算法.原因在于,MOEA/D-LR算法首先根据新解到方向向量的垂直距离确定替换邻域,且新解在对应的邻域内只替换一次,避免了解集副本过多,多样性下降的情况,该策略有效地维持了解的多样性.其次,新解替换掉旧解后,被替换掉的旧解没有被立刻丢弃,而是在剩下的替换邻域内递归查找,是否该旧解能够替换邻域内的其他解.该递归替换寻优策略可以保证最终被丢弃的解是邻域内最差的解,有效避免了舍弃较优解,保留较差解,从而极大提高解的收敛性. 表2 20次运行的HV的统计结果Table 2 Statistical results of IGD for 20 runs 图2 20次运行的HV盒图Fig.2 Box plots of HV with 20 runs 4.3.2 HV指标对比 表2列出了每个算法在每个测试函数上20次运行的HV均值和标准差.分析表2的数据可得,除测试函数WFG2和WFG3外,MOEA/D-LR算法获得了所有函数的最大HV均值,这说明MOEA/D-LR算法求解到的Pareto前沿近似解集具有良好的收敛性和分布性,性能明显优于四个比较算法.图2绘制了所有算法20次运行的HV盒图,分析图2中的盒图可得,除WFG2和WFG3外,MOEA/D-LR算法的中位数均大于四个比较算法,并且该算法的四分位距较小,说明其求解的精度和鲁棒性好.此外,MOEA/D-LR算法产生的异常点也明显少于其他四个比较算法,这同样证明了该算法具有良好的鲁棒性. 4.3.3 Pareto前沿对比分析 为直观显示出MOEA/D-LR算法收敛性的提高,使用20次运行中IGD最小的那次实验数据,绘制出MOEA/D,MOEA/D-LR在WFG1-WFG9测试问题上的近似Pareto前沿与真实Pareto前沿对比图.其中细线表示理想的Pareto前沿,圆圈和三角形分别表示MOEA/D和MOEA/D-LR算法求得的Pareto最优解,每幅图中的小图代表部分区域进行放大后的子图.从上述Pareto前沿对比图可以看出,MOEA/D-LR算法求得的解集比原始的MOEA/D求出的解集更接近理想的Pareto前沿,在WFG1、WFG6测试问题上尤为突出.其中MOEA/D-LR在WFG6上求得的解集十分接近真实的Pareto前沿,而MOEA/D求得的解集距离真实的Pareto前沿较远,原因在于当进化代数为250代时,MOEA/D-LR算法在WFG6上已接近完全收敛,而MOEA/D由于进化代数不够,未收敛于理想的Pareto前沿,这同样证明了递归替换寻优策略能够极大提高算法的收敛性. 图3 WFG系列Pareto对比图Fig.3 Comparison chart of Pareto on WFG 表3 20次运行的HV和S的统计结果Table 3 Statistical results of HV and S for 20 runs 图4 五种算法在WFG问题上的IGD变化趋势Fig.4 IGD trend of five algorithms on WFG 在表3中,对MOEA/D和MOEA/D-LR算法HV均值和标准差进行比较可得,MOEA/D-LR的HV均值均大于MOEA/D,表明该算法的整体性能明显优于MOEA/D算法.除DTLZ1和DTLZ6外,MOEA/D-LR的标准差均小于MOEA/D,表明该算法具有良好的鲁棒性.从指标S的数据可得,在测试函数DTLZ1,DTLZ2和DTLZ4上,MOEA/D-LR算法的S指标值明显小于MOEA/D算法,表明改进算法MOEA/D-LR具有良好的分布性,在测试函数DTLZ6上,改进算法的分布性略优于原始的MOEA/D算法.此外,MOEA/D-LR算法的S指标值标准差非常小,这同样也表明该算法的鲁棒性强. 为进一步探究MOEA/D-LR算法的性能,本文给出了MOEA/D-LR和四个比较算法在WFG系列测试函数上IGD指标值随种群进化代数的变化曲线图,其中横坐标是种群的进化代数,纵坐标是20次运行的IGD均值.本文以三个测试函数(WFG1、WFG4、WFG8)为例进行分析,结果如图4所示.从图中观察可得,MOEA/D-LR算法在收敛速度和最终的收敛结果上都要优于四个比较算法.由图4(a)可得,在测试函数WFG1上,当进化代数为250代左右时,MOEA/D-LR算法的收敛速率明显提高,IGD均值非常小,这表明该算法已接近完全收敛,而其他四个比较算法的IGD均值均较大,表明这四个比较算法在同等迭代次数上均未完全收敛,并且,MOEA/D-LR算法的整体收敛速度明显快于其他四个比较算法.观察图4(a-c)前几代的IGD变化曲线图可得,三角形的下降速度明显快于另外四种形状,说明引入递归替换寻优策略后,在种群进化的初期阶段,对促进种群的收敛有着显著的效果,MOEA/D-LR算法能够有效地促进种群的进化,提高算法所求解集的收敛性. 为维持算法多样性的同时提高算法的收敛性,提出基于递归替换寻优策略的MOEA/D-LR算法.该算法根据新解到对应方向向量的垂直距离确定替换邻域,保持解在目标空间中的均匀分布,有效维持解集的多样性;采用递归替换寻优策略对邻域内的解集进行替换,尽可能快速引导解集朝Pareto前沿进化,提高解的收敛性.实验结果表明,MOEA/D-LR算法的Pareto前沿近似解集更逼近真实的Pareto前沿,解集的分布性也更好,性能明显优于其他四个比较算法.在接下来的工作中,我们将考虑对MOEA/D-LR算法进行扩展以探究其在高维多目标优化问题上的性能. : [1] Zheng Jin-hua.Multi-objective evolutionary algorithm and its application[M].Beijing:Science Press,2007. [2] Eiben A E,Smith J E.Introduction to evolutionary computing[M].Springer:Berlin,2003. [3] Ishibuchi H,Sakane Y,Tsukamoto N,et al.Evolutionary many-objective optimization by NSGA-II and MOEA/D with large populations[C].IEEE International Conference on Systems,Man and Cybernetics,IEEE Press,2009:1758-1763. [4] Gong Mao-guo,Jiao Li-cheng,Yang Dong-dong,et al.Research on evolutionary multi-objective optimization algorithms[J].Journal of Software,2009,20(2):271-289. [5] Gong D W,Liu Y P,Sun X Y,et al.Parallel many-objective evolutionary optimization using objectives decomposition[J].Acta Automatica Sinica,2015,41(8):1438-1451. [6] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197. [7] Zitzler E,Laumanns M,Thiele L.SPEA2:improving the strength pareto evolutionary algorithm[C].Evoltionary Methods for Design,Optimisation and Control,Spain,2002:95-100. [8] Zhang Q,Li H.MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J].IEEE Transactions on Evolutionary Computation,2007,11(6):712-731. [9] Li H,Zhang Q.Multiobjective optimization problems with complicated pareto sets,MOEA/D and NSGA-II[J].IEEE Transactions on Evolutionary Computation,2009,13(2):284-302. [10] Qi Y,Ma X,Liu F,et al.Moea/d with adaptive weight adjustment[J].Evolutionary Computation,2014,22(2):231-264. [11] Li K,Zhang Q,Kwong S,et al.Stable matching-based selection in evolutionary multiobjective optimization[J].IEEE Transactions on Evolutionary Computation,2014,18(6):909-923. [12] Wang Z,Zhang Q,Gong M,et al.A replacement strategy for balancing convergence and diversity in MOEA/D[C].Proceedings of IEEE Congress on Evolutionary Computation,Beijing,2014:2132-2139. [13] Yuan Y,Xu H,Wang B,et al.Balancing convergence and diversity in decomposition-based many-objective optimizers[J].IEEE Transactions on Evolutionary Computation,2015,20:1-1. [14] Zhou A,Zhang Q.Are all the subproblems equally important?Resource allocation in decomposition-based multiobjective evolutionary algorithms[J].IEEE Transactions on Evolutionary Computation,2016,20(1):52-64. [15] Zhang Y,Hu S,Wu J,et al.Multi-objective optimization of double suction centrifugal pump using Kriging meta models[J].Advances in Engineering Software,2014,74(4):16-26. [16] Messac A,Ismail-Yahaya A,Mattson C.The normalized normal constraint method for generating the Pareto frontier[J].Struct Multidisc.Optim,2003,25:86-98. [17] Jan M A,Khanum R A.A study of two penalty-parameterless constraint handling techniques in the framework of MOEA/D[J].Applied Soft Computing,2013,13(1):128-148. [18] Zhang Q,Liu W,Li H.The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances[C].Evolutionary Computation,CEC ′09,IEEE Congress on,IEEE,2009:203-208. [19] Huband S,Barone L,While L,et al.A scalable multi-objective test problem toolkit[J].Lecture Notes in Computer Science,2005,3410:280-295. [20] Deb K,Thiele L,Laumanns M,et al.Scalable multi-objective optimization test problems[C].Evolutionary Computation,CEC ′02,Proceedings of the 2002 Congress on,IEEE,2002:825-830. [21] Bosman P A N,Thierens D.The balance between proximity and diversity in multiobjective evolutionary algorithms[J].IEEE Transactions on Evolutionary Computation,2003,7(2):174-188. [22] Veldhuizen D A V,Lamont G B.On measuring multiobjective evolutionary algorithm performance [C].Evolutionary Computation,Proceedings of the 2000 Congress on,IEEE,2000,1:204-211. [23] Deb K,Agrawal R B.Simulated binary crossover for continuous search space[J].Complex Systems,2000,9(2):115-148. 附中文参考文献: [1] 郑金华.多目标进化算法及其应用[M].北京:科学出版社,2007. [4] 公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报,2009,20(2):271-289.4 仿真实验及结果分析
4.1 测试函数及参数设置
4.2 性能评价指标
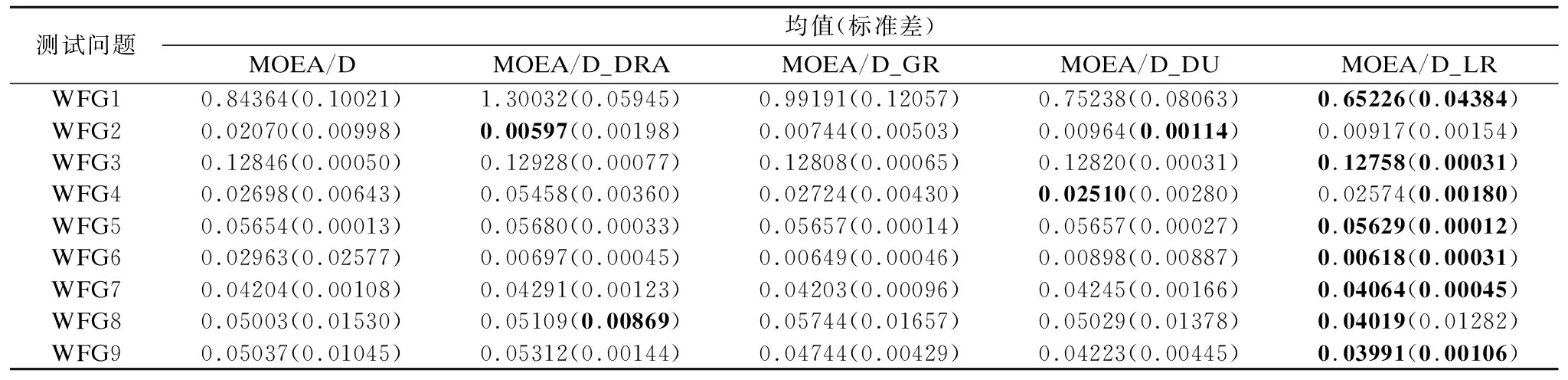
4.3 改进算法在WFG函数上性能对比分析

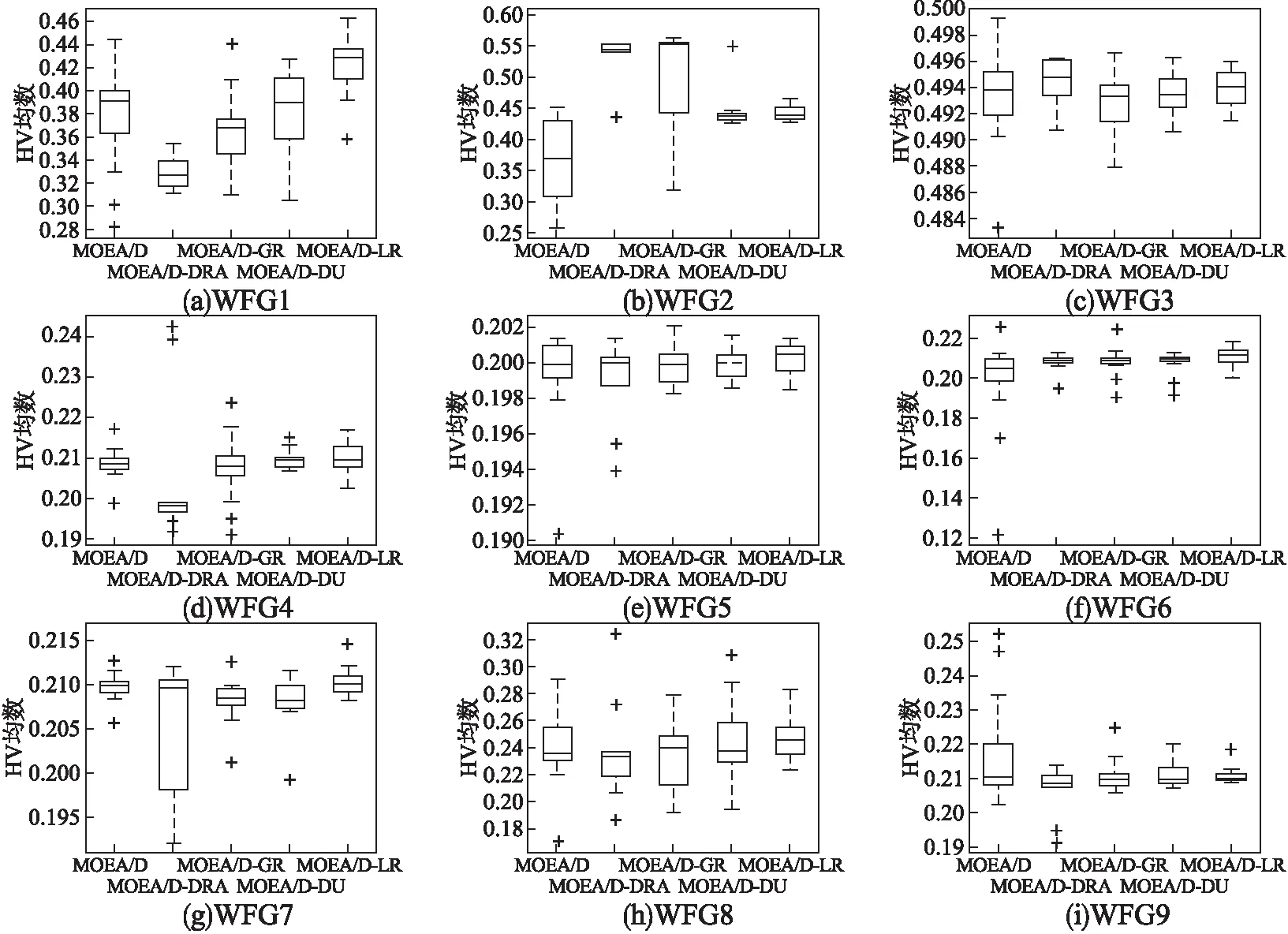



4.4 改进算法在DTLZ函数上性能对比分析
4.5 WFG函数IGD指标值的进化情况
5 结 论

