基于MATLAB的波浪补偿平台动力学分析

唐刚， 李庆中， 杨志启， 胡雄

(上海海事大学物流工程学院，上海 201306)

0 引 言

起重机波浪补偿装置的研究是一个经典的课题。国外研究机构在波浪补偿系统方面的研究最早是在“二战”后期开始的，当时还只是停留在理论研究上，后来转入了试验研究,并开发了一系列具有波浪补偿功能的起重机(例如T-ACS系列起重船[1])。NEUPERT 等[2]提出了一种基于起伏运动预测策略和基于反馈策略的升沉补偿控制系统，并进行了仿真研究。ADAMSON等[3]针对波浪补偿系统中存在的多种问题提出了不同的解决办法。金栋平等[4]对起重装置上的绳索进行了动力学分析，总结了在对绳索系统进行动力学建模与控制时所遇到的问题。方晓旻[5]建立了不同海况下船舶的运动模型,分析了船舶的运动规律,并分析了波浪补偿装置对起重机的影响,最终用可编程逻辑控制器(programmable logic controller, PLC)实现了对电气控制系统的设计。李震震[6]建立了基于波浪谱激励模型的起重机吊物的精确非线性动力学模型,实现了对物体的主动控制。电动补偿控制系统[7-8]具有很好的快速响应性、适应性，是波浪补偿控制中的热点和趋势。

目前，很多海上工作船都具备动力定位系统，这不仅使船舶的纵横摇晃得到一定的控制，还可以把纵倾、横倾运动转化为升沉方向的运动，因此对船舶运动的补偿就主要是升沉补偿[9]，但很难对船舶本身垂直方向上的升沉运动进行补偿[10]。针对两船之间的相对上升下降运动，现在的海上作业需要更高精度和可靠性且操作简单的起重机波浪补偿装置，其中波浪补偿控制系统是最核心的部分，其控制性能的好坏直接影响波浪补偿的效果,因此设计具有快速响应性、适应性的电动补偿控制系统具有重要意义。

1 波浪补偿平台设计

1.1 工作原理

在海上起重机作业过程中，其吊物起升与降落时，船舶本身会产生升沉方向上的运动，同时由于波浪的影响，两船之间也会产生升沉方向上的相对运动，因此要对船舶起重过程中升沉方向上的运动进行控制补偿。

许多船舶上有起重机(又称卷扬机、绞车)，起重机内部装有一个差动行星齿轮减速器用来带动滚筒从而提升重物，太阳轮和内齿轮为输入端，行星架为输出端。由行星齿轮传动原理可知，当太阳轮与内齿轮转向相同(相反)时，行星架转速增加(降低)。在太阳轮的输入控制上，船舶起重机与普通地面液压起重机的不同体现在运动控制算法上，船舶起重机采用波浪补偿控制算法。内齿轮液压电机的输出功率(转动扭矩)小于太阳轮的输入功率。当两侧电机同向驱动时，起重机转速增加；随着两侧电机驱动方向的改变，起重机转速也随之改变。根据海上情况及作业情况，由传感器的反馈控制电机的输出，以此控制减速器。利用这个原理改变重物的升降速度来实现波浪补偿，减小作业时的晃动。[11]

在没有风浪的情况下，内齿轮的制动器处于闭合状态, 内齿轮不旋转。这时减速器就是典型的NGW型行星齿轮减速器，与地面起重设备的工作情况一样，太阳轮作为输入端、行星架作为输出端为起重机提供动力，以完成正常的升降工作。在波浪较大时，通过反馈调节控制内齿轮的驱动力矩，形成波浪补偿系统。

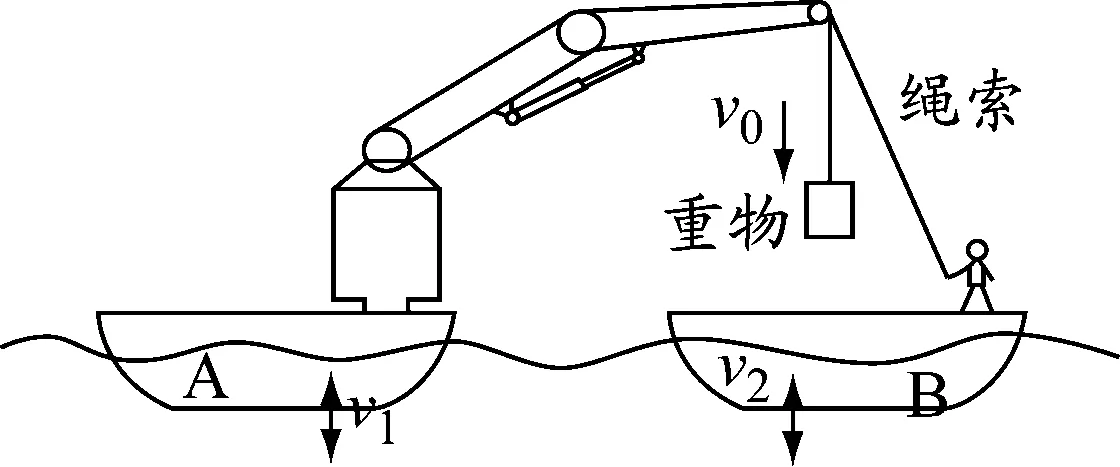
图1 起重机升沉补偿示意图

起重机升沉补偿示意图见图1。起重机工作时，提供给重物的垂直升降速度为vR=v0+v1-v2，其中v0为起重机收放速度，v1和v2分别为供货船A和被供货船B的摇摆速度在垂直方向上的分量。只要vR与v1-v2无关，重物就能稳定地从供货船移动到被供货船上。波浪补偿就是要实现此目标。

1.2 坐标变换

1.2.1 坐标系建立和转化

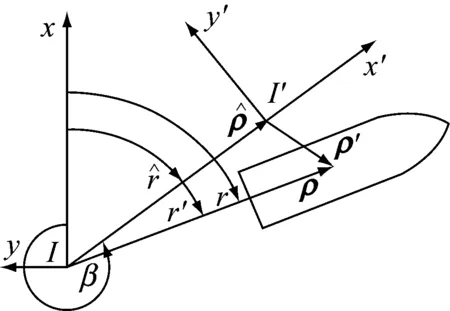
图2 船舶惯性坐标系和随流漂移坐标系

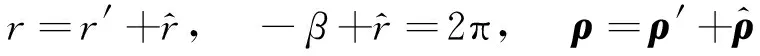
本文用到的惯性坐标系可以是一个真实存在的、静止不动的坐标系，也可以是一个慢慢稳定移动的坐标系。它们对下面的运算结果没有影响。[12-13]

1.2.2 姿态矩阵与坐标变换

为求得船舶运动，定义动坐标系O-xyz和参考坐标系O-XYZ。动坐标系O-xyz与船舶固联,随船体一起上下左右摇晃，其坐标原点O位于船舶重心，x轴沿船纵向并指向船的航向，y轴沿船横向并指向船的右侧边，z轴沿船底板垂向并指向正下方。

参考坐标系O-XYZ是随船舶以船速运动的，但是不随船舶一起晃动，只作平动，始终位于平衡状态。它构成了表达船舶晃动位移和姿态的基准。当船舶不晃动时两坐标系重合，当船舶晃动时两坐标系分开。参考坐标系O-XYZ经3次转动后可变换为动坐标系O-xyz：O-XYZ绕Z轴转动角度Ψ到O-X1Y1Z，O-X1Y1Z绕Y1轴转动角度θ到O-xY1Z1，O-xY1Z1绕x轴转动角度φ到动坐标系O-xyz。这里，Ψ、θ和φ分别为船舶的首摇角、横摇角和纵摇角。

根据空间直角坐标系坐标变换关系，可得到3次转动过程中的变换方程组:

(1)

(2)

(3)

整理得

(XYZ)T=A(xyz)T

(4)

其中参考坐标系变换为动坐标系的变换矩阵

(5)

船舶陀螺仪(角速度传感器)测量的数据为船体沿三轴向的角加速度ωx、ωy和ωz。为得到变换矩阵A，应先求得船舶运动姿态角Ψ、θ和φ。

应用刚体动力学相关知识可以得到，角速度矢量ω在动坐标系O-xyz上的投影为

(6)

解得

(7)

用典型的四阶龙格库塔法求解微分方程组(7)，可得Ψ、θ和φ，进而得到A。利用式(4)，可将动坐标系下的船舶运动加速度变换为参考坐标系下的船舶运动加速度，对加速度进行积分即可得到参考坐标系下船舶运动的方位速度，再次积分即可得到参考坐标系下船舶运动的位移。

2 波浪补偿平台的动力学分析

2.1 机械执行机构模型

船舶利用2K-H (NGW) 型行星齿轮减速器作为差动行星齿轮传动系统(简称差动行星轮系)[14-16]。K代表中心轮，H代表行星架，2K-H即为由2个中心轮、1个太阳轮和1个行星架构成的行星齿轮传动机构。根据传动比将其分为正号传动机构(在传动比小于零和行星架固定不动时，2个中心轮的旋转方向相同)和负号传动机构(在传动比大于零和行星架固定不动时，2个中心轮的旋转方向相反)。

2.1.1 差动行星轮系调速特性

由于NGW型行星齿轮减速器的行星架并非定轴传动，不能直接用定轴传动的计算公式计算传动比，但可以采用行星架固定法计算。设2个中心轮的转速分别为na和nb，行星架的转速为nH，太阳轮与行星架的旋转方向相同，顺时针方向为行星齿轮旋转的正方向。当给差动行星轮系整体加一个转速-nH(与行星架转速大小相同、方向相反)时，行星架H的转速为

(8)

其中u0为传动比。因此，差动行星轮系的最高输出转速与最低输出转速之比为

(9)

2.1.2 差动行星轮系数学模型

采用集中质量模型。模型广义坐标分别为：太阳轮的角位移为θs、第i个中心轮pi的角位移为θpi(i=1, 2)和行星架H的角位移θH。由拉格朗日第二类微分方程可导出差动行星轮系动力学微分方程：

(10)

式中：Js、Jpi和JH分别为太阳轮、中心轮和行星架的转动惯量；rbs为太阳轮齿轮的基圆半径；rbps为中心轮基圆半径；rH为行星架半径；m为质量；α为齿轮副啮合角；TD为输入转矩；TL为负载转矩；D和P分别为齿轮啮合过程中的黏性啮合力和弹性啮合力，下标spi表示太阳轮与中心轮的啮合，下标rpi表示行星架与中心轮的啮合。

2.2 伺服驱动系统模型

2.2.1 步进电机速度控制

步进电机的基本特点是将脉冲序列信号变换成轴向位置的角度增量。[17-18]当脉冲数量一定时,其转轴转动角度相应确定，它们之间呈线性关系。因此,可对步进电机进行开环控制。

绕组电路的基本方程为

(11)

式中：R、V1、I1、L1和μ1分别为绕组电阻、电压、电流、自感和反电动势。 用式(11)可以求解A、B两个绕组电路。A相绕组的电磁转矩为

(12)

式中：θe为机械角；kt0和ktc分别为转矩因数和饱和因数；h3为电磁转矩的三次谐波相对幅值。TB与TA的求解公式相同。定位转矩为

Td=Dsin(4θe)

(13)

式中：D为定位转矩的幅值。因此，步进电机的总转矩为

TE=TA+TB+Td

(14)

它与外部负载转矩TL间的动力学方程为

(15)

(16)

式中：C为黏滞阻尼系数；δ为转子位置角；ω为转子机械角速度；J为电机系统转动惯量。

2.2.2 步进电机传递函数

步进电机的传递函数可以直接表示为

(17)

式中：Tr(s)为波浪补偿系统给定力矩。

对于磁场控制式步进电机，电机转矩TE与励磁电流If的关系为

TE(s)=KmIf(s)

(18)

式中：Km为电机常数。若忽略反电动势，则可得到磁场电压与励磁电流的关系为

(19)

转矩时间常数τf=Lf/Rf，其中Rf和Lf分别为励磁电阻和励磁电感。因此，步进电机的传递函数为

(20)

3 基于MATLAB的波浪补偿平台控制仿真

PID控制就是按照给定的跟踪轨迹误差的比例(P)、积分(I)、微分(D)进行控制。PID控制系统原理图见3。PID控制系统的输入量e(t)为系统误差，e(t)=r(t)-c(t)，其中c(t)为系统的实际输出量，r(t)为系统的给定量。系统偏差u(t)是经过PID控制系统计算后的系统输出量，直接作用于被控对象。

图3 PID控制系统原理图

PID控制是一种线性控制方法，其输出量u(t)可表达为

(21)

式中：ki为积分时间常数；kp为比例系数；kd为微分时间常数。

为对波浪补偿系统进行PID控制，对式(21)进行离散化处理，得到式(22)。只有采样周期t0足够小，准确度才会更高。

(22)

PID控制算法有位置式和增量式两种：位置式PID控制算法以执行机构的位置为输出量；增量式PID控制算法以执行机构位置的增量为输出量。由于本文波浪补偿平台仿真的执行机构是步进电机，需要输出控制量的增量，所以选用增量式PID控制算法[19-24]。

(23)

式中：Δe(k)=e(k)-e(k-1)。

由式(20)可知,步进电机的传递函数为

(24)

设采样时间为0.01 s，在用MATLAB对波浪补偿平台进行仿真分析后，得到期望轨迹：

x=1.63-0.5cos(πt/5)

y=1.8+0.5sin(πt/5)

图4和5给出了该波浪补偿系统动力学模型在PID控制下的轨迹追踪效果及其误差。仿真结果表明：在使用PID控制算法时，该波浪补偿系统能够迅速响应输入的变化；使用PID控制算法控制波浪补偿系统，有速度快、稳定性高和精确度高的优点。

图4 用PID控制的轨迹追踪效果图5 用PID控制的轨迹追踪误差

4 结 论

在波浪补偿平台方案设计的基础上，设立了表现波浪补偿平台控制性能的动力学模型。选用起重机模型为该系统的机械执行机构模型，采用差动行星齿轮传动系统实现对平台调速的控制，利用步进电机模型模拟实现对伺服驱动系统输入的控制，建立伺服、调速、执行的电动自动补偿控制系统。利用PID控制算法对该系统进行控制，借助MATLAB进行轨迹跟踪仿真，结果发现，PID控制系统具有良好的快速性和稳定性，能够很好地满足波浪补偿平台的要求。

参考文献：

[1] MASOUD Z N. A control system for the reduction of cargo pendulation of ship-mounted cranes[D]. Blacksburg, Virginia: Virginia Polytechnic Institute and State University, 2000.

[2] NEUPERT J, MAHL T, HAESSING B,etal. A heave compensation approach for offshore cranes[C]//American Control Conference. Seattle Washington, June 11-13 2008. IEEE, 2008: 538-543.

[3] ADAMSON J E. Efficient heave motion compensation for cable-suspended systems[C/OL]//Marine Technology Society. Conference on Underwater Intervention, 2003: 1-7.

[4] 金栋平, 文浩, 胡海岩. 绳索系统的建模、动力学和控制[J]. 力学进展, 2004, 34(3): 304-313.

[5] 方晓旻. 船用起重机和波浪补偿控制系统设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.

[6] 李震震. 船用起重机吊物波浪补偿控制研究[D]. 大连: 大连理工大学, 2014.

[7] 芦红威. 海洋工程大型起重设备及其关键技术研究[J]. 现代工业经济和信息化, 2016(23): 47-48.

[8] 吴隆明. 深海作业起重机主动式升沉补偿控制系统的研究与开发[D]. 广州: 华南理工大学, 2012.

[9] 祝福, 刘晓林. 船用起重机主动式升沉补偿控制的研究[J]. 船电技术, 2016, 36(4): 30-32.

[10] 陈远明, 叶家玮, 魏栋. 波浪运动补偿稳定平台系统的试验研究[J]. 机床与液压, 2008, 36(4): 67-70, 100.

[11] 孙智民, 季林红, 沈允文. 2K-H行星齿轮传动非线性动力学[J]. 清华大学学报(自然科学版), 2003, 43(5): 636-639. DOI: 10.16511/j.cnki.qhdxxb.2003.05.015.

[12] 齐凯. 空间六自由度位姿调整平台运动性能研究[D]. 重庆: 重庆大学, 2016.

[13] 方喜峰, 赵若愚, 吴洪涛, 等. 6-UPS交叉杆型并联机床的运动学正解算法[J]. 机械工程学报, 2012, 48(13): 56-60. DOI: 10.3901/JME.2012.13.056.

[14] YURT S N, ANLI E, OZKOL I. Forward kinematics analysis of the 6-3 SPM by using neural networks[J]. Meccanica, 2007, 42(2): 187-196. DOI: 10.1007/s11012-006-9037-3.

[15] 蔡黎明. 滑动轴承支撑的行星齿轮传动系统均载特性分析研究[D]. 南京: 南京航空航天大学, 2010.

[16] 韩翔. 基于UG的2K-H行星减速器计算机辅助设计[D]. 成都: 西南交通大学, 2004.

[17] 韩利虎. 浅谈步进电机的基本原理[J]. 内蒙古石油化工, 2007(11): 240.

[18] 陈志聪. 步进电机驱动控制技术及其应用设计研究[D]. 厦门: 厦门大学, 2008.

[19] 谭鹏. 桥式起重机智能防摆控制技术研究[D]. 南京: 南京航空航天大学, 2015.

[20] 侯鹏强. 基于模糊PID控制的多电机同步控制研究与实现[D]. 成都: 电子科技大学, 2010.

[21] 徐小军, 陈循, 尚建忠, 等. 单神经元PID的波浪补偿系统自适应控制与仿真[J]. 机械与电子, 2009(8): 61-64.

[22] 窦艳艳, 钱蕾, 冯金龙. 基于Matlab的模糊PID控制系统设计及仿真[J]. 电子科技, 2015, 28(2): 119-122.

[23] KUMAR V, RANA K P S. Nonlinear adaptive fractional order fuzzy PID control of a 2-link planar rigid manipulator with payload[J]. Journal of the Franklin Institute, 2017, 354(2): 993-1022.

[24] CORON J M, TAMASOIU S O. Feedback stabilization for a scalar conservation law with PID boundary control[J]. Chinese Annals of Mattematics, Series B, 2015, 36B(5): 763-776. DOI: 10.1007/s11404-015-0975-8.