内置工字钢骨方钢管混凝土自由扭转刚度计算与FEM验证

张文福, 李 洋, 邓 云, 刘迎春, 邓世林, 李明亮, 严 威

( 1. 南京工程学院 建筑工程学院，江苏 南京 211167； 2. 东北石油大学 土木建筑工程学院，黑龙江 大庆 163318 )

0 引言

现代建筑结构朝着超高、大跨方向发展，对结构的主要承载力构件的受力性能提出新的要求，为新型组合构件的生产提供条件，如内置钢骨钢管混凝土构件。这种混凝土构件将钢骨插入钢管并填满混凝土，由于受内置钢骨、混凝土和外围钢管的相互作用，混凝土的抗压强度和钢材的抗拉强度得到充分利用，实现优势互补，构件的整体受力性能、承载力、刚度、延性及耗能能力得到改善和提高，因此内置工字钢骨方钢管混凝土构件被广泛应用于桥梁结构、高层建筑、工业厂房和大跨度空间结构[1]。

人们对钢管混凝土受弯构件的试验及理论研究较多。韩林海[2]研究钢管高强混凝土纯弯曲构件力学性能及承载力。计静等[3]对配钢管高强混凝土芯柱的异强组合短柱轴压性能进行数值模拟。计静等[4]研究矩形钢管混凝土翼缘的H型蜂窝组合柱特征值屈曲性能。Shekastehband B等[5]研究在双层空心钢管混凝土柱中加纵向加劲肋的抗火性能，纵向加劲肋可以增强混凝土与内外层钢管的粘结作用。Ho-Jun Lee等[6]对薄壁矩形钢管混凝土柱结构性能进行试验研究，分析矩形钢管混凝土柱中加入不同截面形式高强钢薄板对其整体偏心承载力的影响。Ukanwa K U等[7]给出关于钢管混凝土柱在火灾作用下的简化设计程序，提出钢管混凝土柱轴向承载力的简化设计公式。人们研究内置钢骨的钢管混凝土构件受力性能。赵同峰等[8-9]研究基于纤维模型法的方钢管—钢骨高强混凝土抗弯承载力，对方钢管—钢骨高强混凝土偏压柱进行试验研究与理论分析。金松等[10]对钢骨—方钢管高强混凝土组合柱抗剪力学性能进行有限元研究。王清湘等[11]对13根内置钢骨的钢管混凝土组合柱进行轴心受压试验研究。

有关内置钢骨的钢管混凝土受扭构件的研究较少，主要以有限元数值模拟为主。史艳莉等[12-14]利用ABAQUS软件，对内配工字型矩形钢管混凝土双向偏压构件、内配型钢方钢管混凝土轴压短柱，以及十字型钢骨圆钢管混凝土纯扭构件力学性能进行有限元研究。钢及钢—混凝土组合薄壁构件扭转和弯扭屈曲分析的工程理论——板—梁理论[15-19]，为解决钢管混凝土自由扭转和约束扭转提供一种基本理论方法。基于板—梁理论，张文福等[20]对工字型钢—混凝土组合双跨连续梁的弯扭屈曲性能进行分析，研究连续梁发生弯扭屈曲时的临界弯矩。刘迎春等[21]运用能量变分法，研究集中荷载作用下扭转支撑悬臂钢梁弯扭屈曲，给出弯扭屈曲的总势能方程，提出扭转支撑悬臂钢梁临界弯矩计算公式。

基于最小应变能原理[22-23]和板—梁理论，笔者给出内置工字钢骨方钢管混凝土自由扭转刚度的解析解，利用ANSYS软件对内置工字钢骨方钢管混凝土自由扭转刚度进行验证；对自由扭转刚度进行扩展参数分析，分析含钢率、混凝土强度等级等参数对自由扭转刚度的影响。考虑自由扭转刚度解析解的表达式比较复杂，基于叠加原理，给出内置工字钢骨方钢管混凝土自由扭转刚度的简化设计公式。

1 自由扭转刚度

1.1 基本假设

(1)扭转变形前后横截面的形状与垂直于构件轴线的截面投影的形状相同，即满足“刚周边假设”[24-26]；

(2)钢管混凝土梁扭转变形由板—梁理论和Saint-Venant扭转理论确定；

(3)不考虑钢管与混凝土之间的相对滑移，即两者纵向变形是协调的[1]；

(4)钢管与混凝土为理想各向同性材料，符合胡克定律。

1.2 问题描述

内置工字钢骨方钢管混凝土悬臂梁结构见图1，截面尺寸与扭转变形见图2。其中Mt为自由端作用的集中扭矩，L为梁的长度，H为工字钢骨总高度，h为工字钢腹板高度，bf、tf分别为翼缘宽度、厚度，tw为腹板厚度，D、t分别为方钢管边长、壁厚，θ(z)为扭转时截面绕剪切中心(形心)的刚性扭转角。

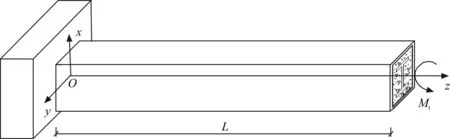
图1 自由端作用集中扭矩的内置工字钢骨方钢管混凝土悬臂梁

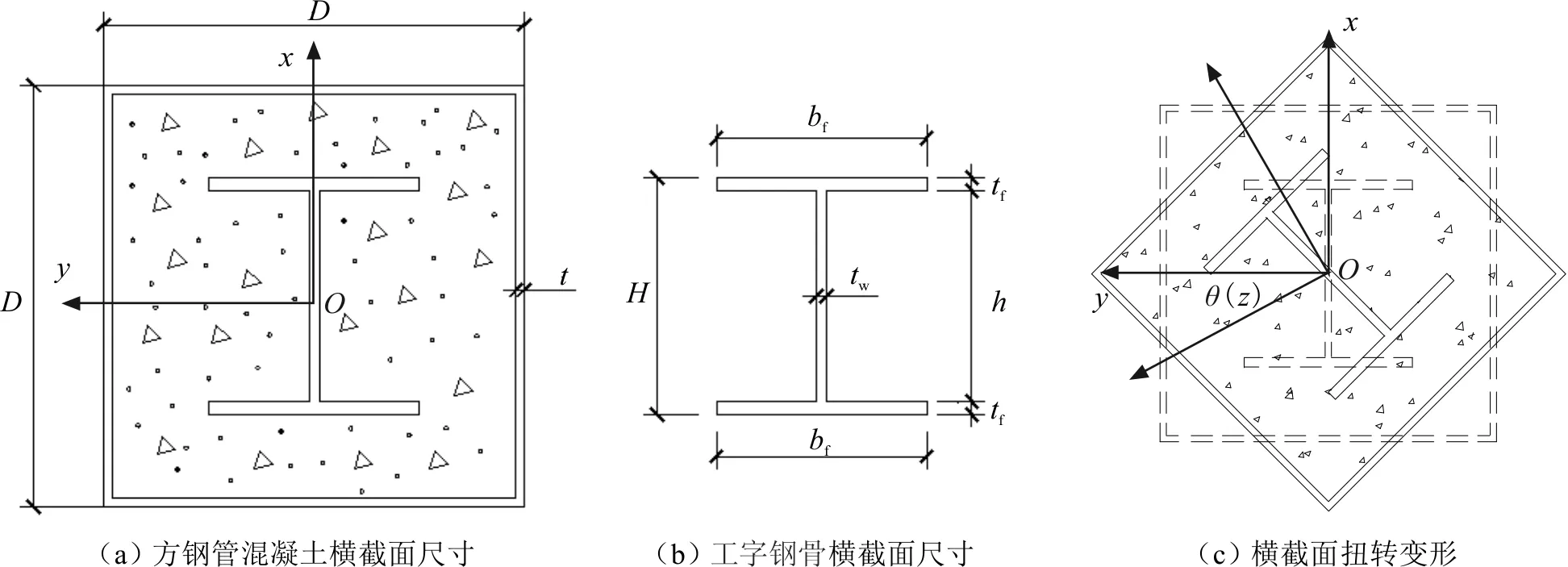
图2 内置工字钢骨方钢管混凝土悬臂梁截面尺寸与扭转变形Fig.2 Sectional diagram and torsional deformation of CFSST with encased I-shaped steel

1.3 自由扭转应变能与扭转刚度解析解

1.3.1 位移场

仅考虑自由扭转，且扭转角的变化率为常数，即内置工字钢骨方钢管混凝土扭率(dθ/dz)为常数的情况。根据基本假设(1)，内置工字钢骨方钢管混凝土截面上任意点沿x、y轴方向的横向位移为

u(y,z)=-yθ,

(1)

v(x,z)=xθ。

(2)

根据基本假设(2-3)，截面上任意点沿z轴方向的纵向位移为

(3)

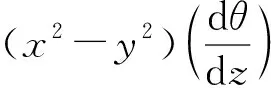
式(3)与实体梁扭转的纵向位移场[19]相似，区别是Vlasov纵向位移仅考虑xy的影响，忽略截面翘曲变形xy的影响，相当于忽略变形约束，因此Vlasov给出的自由扭转刚度偏小。

1.3.2 应变场(几何方程)

根据位移场和弹性力学理论，确定方钢管混凝土截面上任意点的几何方程为

(4)

(5)

(6)

(7)

根据Saint-Venant扭转理论的基本假设，式(7)应为0，即

(8)

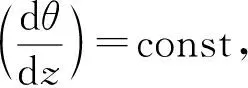
非零应变仅有2个：

(9)

(10)

因此，应变场与Saint-Venant扭转理论完全一致。

1.3.3 物理方程

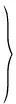
混凝土：τ=Gcγ。

(11)

式中：Gs、Gc分别为工字钢骨、核心混凝土的剪切模量。

1.3.4 应变能

根据弹性力学理论，内置工字钢骨方钢管混凝土的应变能为

(12)

代入非零应变γxz、γyz的表达式，利用分区积分考虑方钢管、核心混凝土及内置工字钢骨的作用。

(1)方钢管应变能为

(13)

积分结果为

(14)

(2)核心混凝土应变能为

(15)

积分结果为

(16)

(3)工字钢骨应变能为

(17)

积分结果为

(18)

内置工字钢骨方钢管混凝土扭转变形总应变能为

Π=Π1+Π2+Π3。

(19)

1.3.5 最小应变能原理

根据最小应变能原理[22-23]，必有

(20)

令m=Gs/Gc，求解可得

(21)

将式(21)代入式(19)，可得内置工字钢骨方钢管混凝土的应变能表达式为

(22)

式中：GJk为内置工字钢骨方钢管混凝土的Saint-Venant扭转刚度或自由扭转刚度，

(23)

2 有限元验证

2.1 自由端扭转角

对于内置工字钢骨方钢管混凝土悬臂梁的扭转问题，可得自由端截面扭转角与集中扭矩关系的表达式为

(24)

式中：θL为自由端截面扭转角。

由式(24)，可以利用有限元方法，对自由端承受一个集中扭矩的内置工字钢骨方钢管混凝土悬臂梁进行静力分析，提取自由端扭转角与理论扭转角，验证文中自由扭转刚度公式的正确性。

2.2 有限元模型

采用ANSYS有限元软件建立模型并进行分析。选取实体单元SOLID45模拟工字钢骨方钢管混凝土梁，单元由8个节点定义，每个节点有3个自由度，即沿节点坐标系x、y和z方向的平动位移[27-28]。管内混凝土选用C40混凝土，弹性模量Ec=32.5 GPa，泊松比μc=0.2；钢材采用Q235，弹性模量Es=206 GPa，泊松比μs=0.3。划分网格时，为同时满足精度和效率要求，整体网格尺寸选为0.05 m(见图3)。边界条件模拟固定端约束，即对一端支座进行全约束。此外，施加荷载时，由于SOLID45单元没有扭转自由度，引入MASS21单元完成自由端集中扭矩的施加(见图4)。

图3 有限元模型网格划分Fig.3 Mesh generation of finite element model

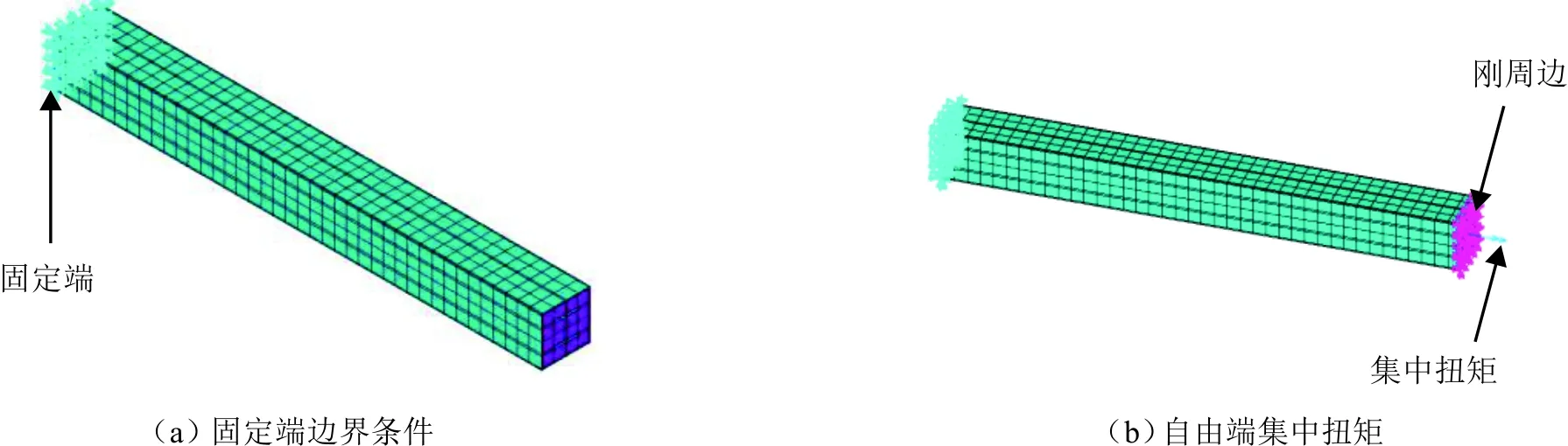
图4 有限元模型边界条件及自由端集中扭矩施加

在自由端集中扭矩作用下，工字钢骨方钢管混凝土悬臂梁有限元模型的整体及截面变形见图5。由图5可以看出，有限元模型的截面变形满足文中理论采用的刚周边假设。

图5 梁整体扭转变形及截面变形

2.3 理论扭转角与有限元扭转角

以方钢管尺寸、内置工字钢骨尺寸为主要变化参数，设计8根不同尺寸的内置工字钢骨方钢管混凝土悬臂梁。根据EN10210 S275J2H & S355J2H《欧洲热轧优质碳素钢管标准》，选取5种不同类型的方钢管尺寸；根据GB/T 11263—2010《热轧H—型钢产品标准》和内置工字钢骨尺寸，选取宽翼缘H—型钢(HW)和中翼缘H—型钢(HM)两种类型。试件设计参数见表1，自由端的理论扭转角和有限元扭转角见表2。

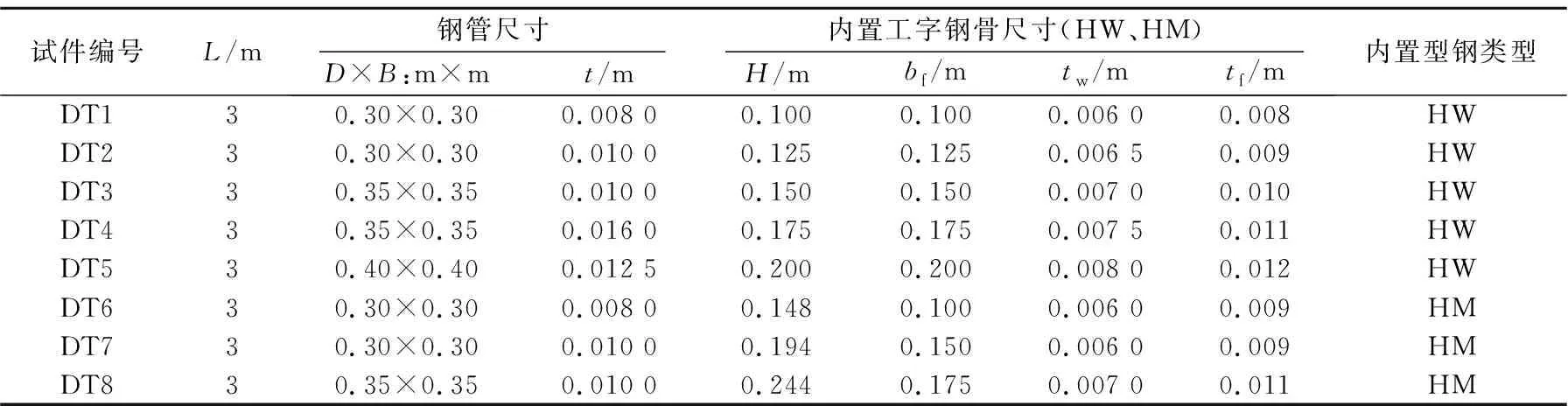
表1 试件设计参数

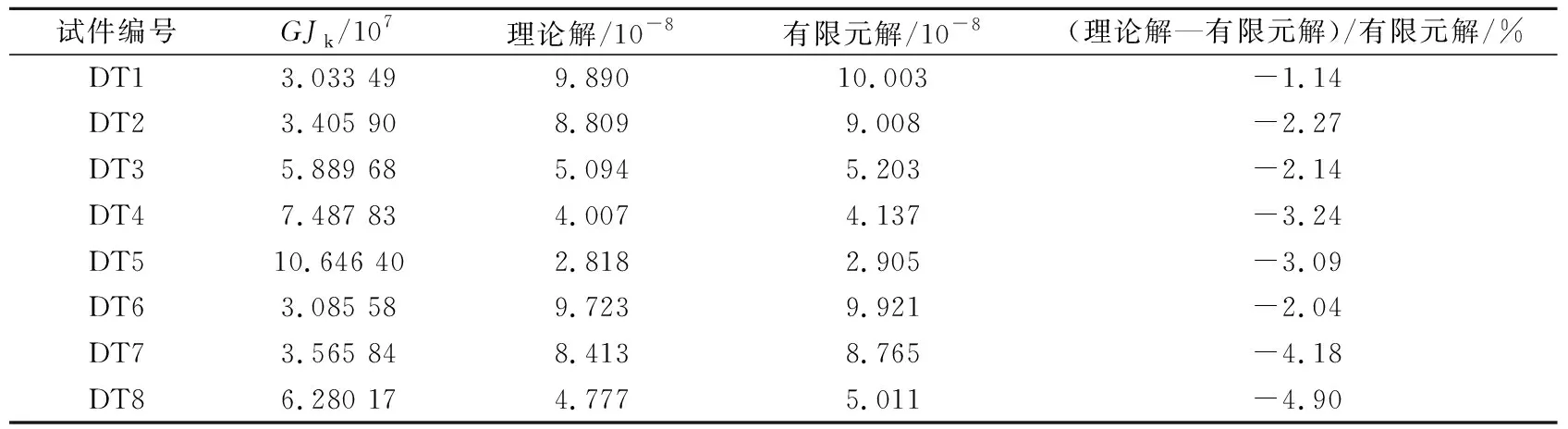
表2 理论扭转角与有限元扭转角计算结果

3 扩展参数分析

由式(23)可见，内置工字钢骨方钢管混凝土悬臂梁的自由扭转刚度GJk，与内置工字钢骨截面尺寸、钢材与混凝土的剪切模量(m=Gs/Gc)和方钢管截面尺寸(D×B)有关。为分析不同参数对自由扭转刚度的影响，主要考虑方钢管的类型(HW、HM)、含钢率s及混凝土强度等参数，其中含钢率为外围钢管面积、内置工字钢骨面积之和与核心区混凝土的面积之比。选取方钢管尺寸D×B为400 m×400 m，壁厚t为12.5 mm；选取工字钢骨为型号HW100×100-HW200×200、HM150×100-HW350×250；选取混凝土强度等级为C30-C80。对内置工字钢骨方钢管混凝土悬臂梁的自由扭转刚度GJk进行扩展参数分析，结果见图6。

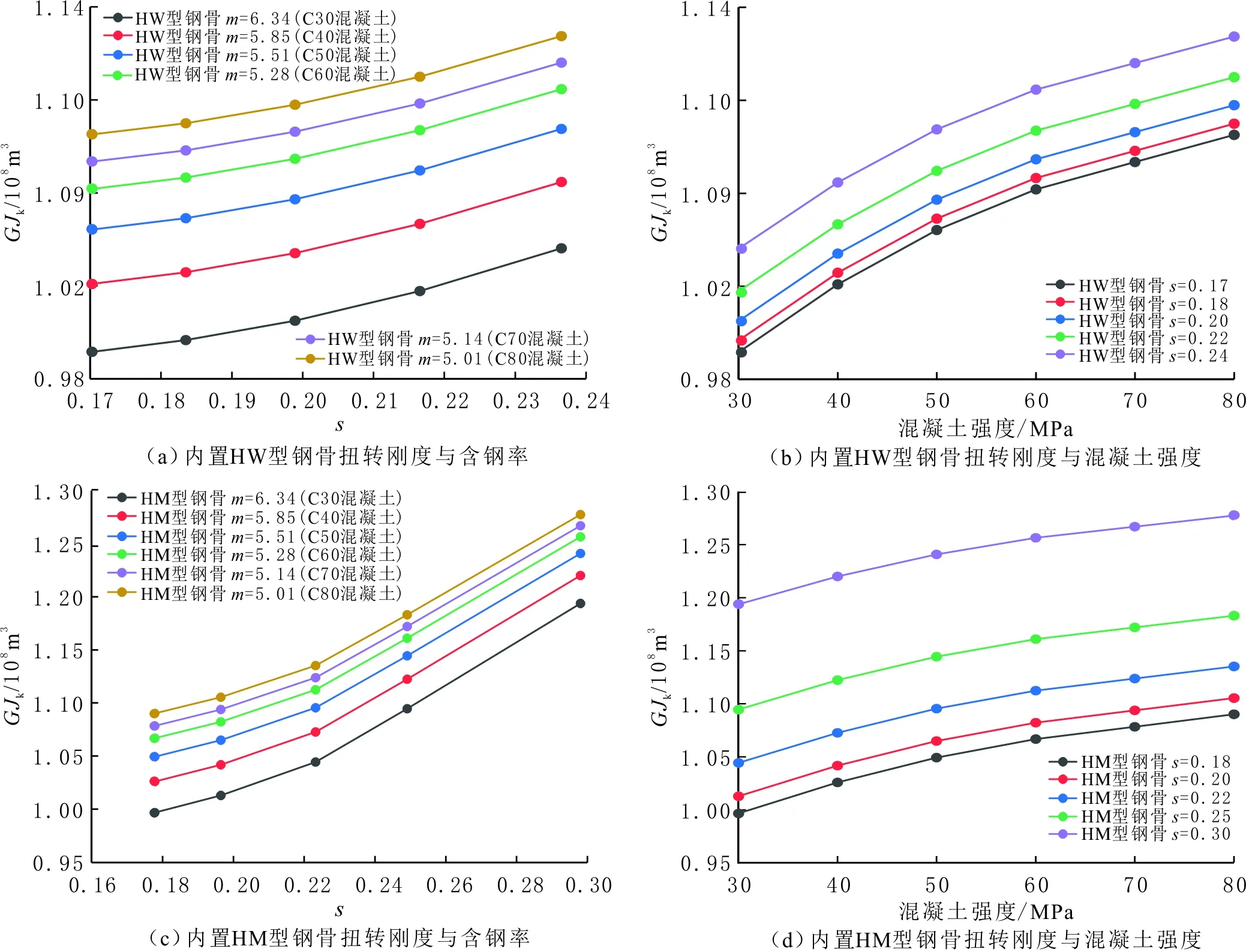
图6 内置工字钢骨方钢管混凝土悬臂梁扭转刚度与含钢率、混凝土强度之间的关系Fig.6 Relationship of torsional rigidity GJk and different parameters

由图6(a、c)可见，内置工字钢骨方钢管混凝土的自由扭转刚度随含钢率的增大而增大，且图6(c)的曲线斜率较图6(a)的大，说明内置HM型钢骨比内置HW型钢骨对自由扭转刚度的影响大，即不同型钢类型对自由扭转刚度有影响。由式(23)可知，内置型钢横截面尺寸的变化对自由扭转刚度GJk影响较大。由图6(b、d)可见，自由扭转刚度随混凝土强度的增大而增大。这是因为随混凝土强度等级增加，混凝土的抗拉抗压弹性模量也随之增大，因此也增大混凝土的剪切模量。由式(23)可知，自由扭转刚度随之增大。由图6可见，当内置型钢为HW型时，图6(b)的混凝土强度与自由扭转刚度曲线的斜率，较图6(a)的含钢率与自由扭转刚度曲线的斜率大，说明混凝土强度对自由扭转刚度的影响比含钢率对自由扭转刚度的影响要大；当内置型钢为HM型时，图6(d)的混凝土强度与自由扭转刚度曲线的斜率，较图6(c)的含钢率与自由扭转刚度曲线的斜率小，说明混凝土强度对自由扭转刚度的影响比含钢率对自由扭转刚度的影响要小。

4 简化设计公式

文中给出的内置工字钢骨方钢管混凝土自由扭转刚度解析解形式复杂。为简化自由扭转刚度理论公式，提出一种计算内置工字钢骨方钢管混凝土自由扭转刚度的简化算法——叠加法。该方法将内置工字钢骨方钢管混凝土自由扭转刚度看作是薄壁方钢管自由扭转刚度、核心混凝土及内置工字钢骨的自由扭转刚度的简单叠加。

根据板—梁理论，文献[27]推导方钢管混凝土的自由扭转刚度表达式为

(25)

其中

(26)

称为方形钢管混凝土量纲一的扭转刚度系数，α为方钢管混凝土的含钢率，α≈4t/D。

(27)

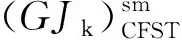
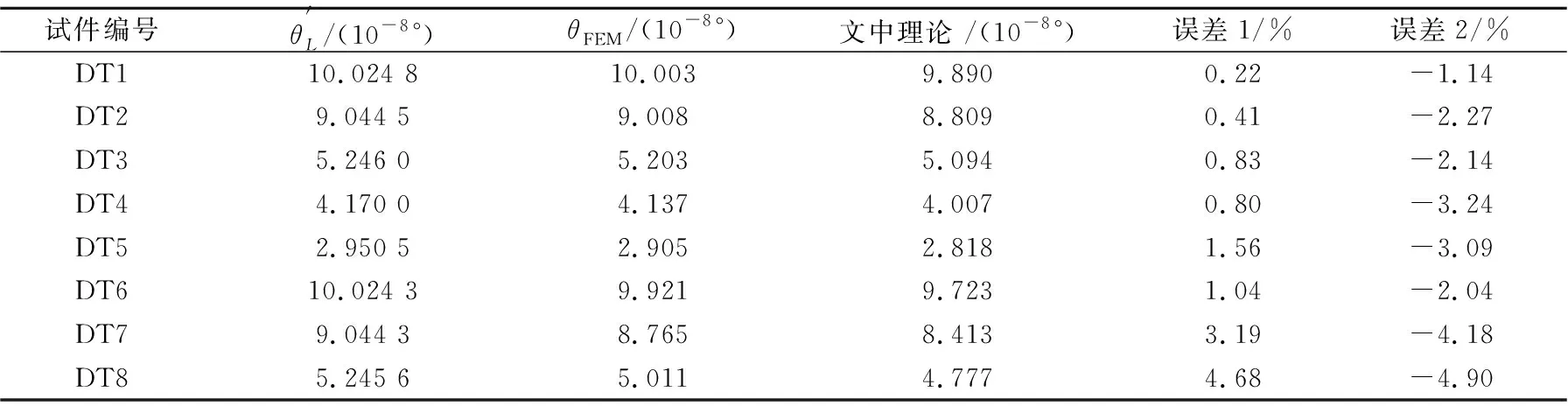
表3 内置工字钢骨方钢管混凝土悬臂梁叠加法扭转角、理论扭转角与有限元扭转角

5 结论

(1)根据Saint-Venant扭转理论和板—梁理论，给出内置工字钢骨方钢管混凝土自由扭转的位移场、应变场和应变能，推导内置工字钢骨方钢管混凝土扭转变形总应变能方程；根据最小应变能原理，求解内置工字钢骨方钢管混凝土的应变能及其自由扭转刚度表达式。

(2)理论公式计算的扭转角与有限元计算的扭转角之间的最大误差不超过5.0%，验证内置工字钢骨方钢管混凝土自由扭转刚度理论公式的正确性。

(3)核心混凝土强度与含钢率对内置工字钢骨方钢管混凝土自由扭转刚度有显著的影响。

参考文献(References)：

[1] 韩林海.钢管混凝土结构—理论与实践[M].3版.北京:科学出版社,2007:1-5.

Han Linhai. Concrete filled steel tubular structures-theory and practice [M]. 3rd ed. Beijing: Science Press, 2007:1-5.

[2] 韩林海.钢管高强混凝土纯弯曲构件力学性能及承载力的研究[J].哈尔滨建筑大学学报,1997,30(1):32-40.

Han Linhai. Study on behavior and flexural capacity of high strength concrete filled steel tubes subjected to pure bending moment [J]. Journal of Harbin University of Civil Engineering & Architecture, 1997,30(1):32-40.

[3] 计静,汪洋,陈晓坤,等.配钢管高强混凝土芯柱的异强组合短柱轴压性能[J].东北石油大学学报,2017,41(5):107-116.

Ji Jing, Wang Yang, Chen Xiaokun, et al. Analysis of axial compression behavior of strength-gradient composite columns with built-in high-strength concrete filled steel tube [J]. Journal of Northeast Petroleum University, 2017,41(5):107-116.

[4] 计静,徐智超,张文福,等.矩形钢管混凝土翼缘的H型蜂窝组合柱特征值屈曲性能[J].东北石油大学学报,2017,41(1):97-105.

Ji Jing, Xu Zhichao, Zhang Wenfu, et al. Eigenvalue buckling analysis of H type honeycombed composite column with rectangular concrete-filled steel tube flange [J]. Journal of Northeast Petroleum University, 2017,41(1):97-105.

[5] Shekastehband B, Taromi A, Abedi K. Fir performance of stiffened concrete filled double skin steel tubular columns [J]. Fire Safety Journal, 2017,88:13-25.

[6] Ho-Jun Lee, In-Rak Choi, Hong-Gun Park, et al. Eccentric compression strength of rectangular concrete-filled tubular columns using high-strength steel thin plates [J]. Journal of Structural Engineering, 2016,143(5):1-11.

[7] Ukanwa K U, Clifton G C, Lim J B P, et al. Simple design procedure for concrete filled steel tubular columns in fire [J]. Engineering Structures, 2018,155:144-156.

[8] 赵同峰,王连广.方钢管—钢骨高强混凝土抗弯承载力分析[J].工业建筑,2008,38(3):27-30.

Zhao Tongfen, Wang Lianguang. Capacity analysis of pure bending of square steel tube filled with steel reinforced high strength concrete [J]. Industrial Construction, 2008,38(3):27-30.

[9] 王连广,赵同峰,李宏男.方钢管—钢骨高强混凝土偏压柱试验研究与理论分析[J].建筑结构学报,2010,31(7):64-71.

Wang Lianguang, Zhao Tongfeng, Li Hongnan. Experimental research and theoretical analysis of square steel tube columns filled with steel-reinforced high-strength concrete subjected to eccentric loading [J]. Journal of Building Structures, 2010,31(7):64-71.

[10] 金松,徐亚丰.钢骨—方钢管高强混凝土组合柱抗剪力学性能研究[J].工业建筑,2016,46(增刊1):990-995.

Jin Song, Xu Yafeng. Shearing study on the properties of shear resistance of square steel tube composite columns filled with steel-reinforced high-strength [J]. Industrial Construction, 2016,46(Supp.1):990-995.

[11] 王清湘,赵大洲,关萍.轴心受压钢骨钢管高强混凝土组合柱力学性能的研究[J].东南大学学报:自然科学版,2002,32(5):710-714.

Wang Qingxiang, Zhao Dazhou, Guan Ping. Research on the mechanical behavior of axially loaded circular steel tube columns filled with steel reingorced high strength concrete [J]. Journal of Southeast University: Natural Science Edition, 2002,32(5):710-714.

[12] 史艳莉,车向龙,王景玄.内配工字型钢的矩形钢管混凝土双向偏压构件参数分析[J].工程力学,2015,32(增刊1):254-260.

Shi Yanli, Che Xianglong, Wang Jingxuan. Parametric analysis on concrete-filled steel tubular columns with internal profile steel under biaxial [J]. Engineering Mechanics, 2015,32(Supp.1):254-260.

[13] 史艳莉,王文达,王亚伟.内配型钢方钢管混凝土轴压短柱力学性能及参数分析[J].工程力学,2014,31(增刊1):201-206.

Shi Yanli, Wang Wenda, Wang Yawei. Mechanical behavior and parametric study of concrete-filled steel tubular stub columns with encased profiled steel under axail compression [J]. Engineering Mechanics, 2014,31(Supp.1):201-206.

[14] 史艳莉,张海龙,王文达.内置钢骨圆钢管混凝土纯扭构件力学性能研究[J].建筑结构学报,2013,34(增刊1):327-331.

Shi Yanli, Zhang Hailong, Wang Wenda. Research on mechanical behavior of concrete-filled steel tubular member with encased profiled steel under pure torsion [J]. Journal of Building Structues, 2013,34(Supp.1):327-331.

[15] 张文福.薄壁梁柱屈曲的板—梁理论[M].北京:科学出版社,2018.

Zhang Wenfu. Plate-beam theory of thin-wall beam and column bulking [M]. Beijing: Science Press, 2018.

[16] 张文福.钢结构稳定理论[M].武汉:武汉理工大学出版社,2017.

Zhang Wenfu. Steel structure stability theory [M]. Wuhan: Wuhan University of Technology Press, 2017.

[17] 张文福.狭长矩形薄板自由扭转和约束扭转的统一理论[EB/OL].中国科技中文在线,http://www.paper.edu.cn/html/releasepaper/2014/04/143.

Zhang Wenfu. Unified theory of free and restricted torsion for narrow rectangular plate [EB/OL]. Chinese Science and Technology Chinese Online, http://www.paper.edu.cn/html/releasepaper/2014/04/143.

[18] 张文福.工字形轴压钢柱弹性弯扭屈曲的新理论[C]//第十五届全国现代结构工程学术研讨会论文集.天津,2015:725-735.

Zhang Wenfu. New theory of elastic flexural-torsional buckling of I-shape axial compression steel column [C]//Proceedings of the 15th National Symposium on Modern Structural Engineering. Tianjin, 2015:725-735.

[19] 张文福.矩形薄壁轴压构件弹性扭转屈曲的新理论[C]//第十五届全国现代结构工程学术研讨会论文集.天津,2015:793-804.

Zhang Wenfu. New theory of elastic flexural-torsional buckling of rectangular thin-wall axial compression member [C]//Proceedings of the 15th National Symposium on Modern Structural Engineering. Tianjin, 2015:793-804.

[20] 张文福,邓云,赵文艳,等.基于板梁理论的工字形钢——混组合双跨连续梁弯扭屈曲分析[J].东北石油大学学报,2017,41(4):107-115.

Zhang Wenfu, Deng Yun, Zhao Wenyan, et al. Flexural-torsional buckling analysis on I-shaped steel-concrete composite double-span continuous beams based on plate-beam theory [J]. Journal of Northeast Petroleum University, 2017,41(4):107-115.

[21] 刘迎春,邓世林,张文福,等.集中荷载作用下扭转支撑悬臂梁弯扭屈曲分析[J].东北石油大学学报,2017,41(3):103-110.

Liu Yingchun, Deng Shilin, Zhang Wenfu, et al. Flexural-torsional buckling analysis for cantilever beam with torsional bracing under concentrated load [J]. Journal of Northeast Petroleum University, 2017,41(3):103-110.

[22] Southwell R V. Castigliano's principle of minimum strain-energy [J]. Proceedings of the Royal Society A, 1936,154(881):4-21.

[23] 卓延文.正则方程与最小应变能原理[J].青岛化工学院学报,1987,8(4):51-58.

Zhuo Yanwen. Canonical equation and principle of least strain energy [J]. Journal of Qingdao Institute of Chemical Technology, 1987,8(4):51-58.

[24] Trahair N S. Flexural-torsional buckling of structures [M]. London: Chapman & Hall, 1993.

[25] 陈骥.钢结构稳定:理论和设计[M].5版.北京:科学出版社,2011.

Chen Ji. Stability of steel structure theory and design [M]. 5th ed. Beijing: Science Press, 2011.

[26] 童根树.钢结构平面外稳定[M].北京:中国建筑工业出版社,2007.

Tong Genshu. Out-plane stability of steel structure [M]. Beijing: China Building Industry Press, 2007.

[27] 张文福,陈克珊,宗兰,等.方钢管混凝土自由扭转刚度的有限元验证[C]//第25届全国结构工程学术会议论文集.包头,2016:465-468.

Zhang Wenfu, Chen Keshan, Zong Lan, et al. Finite element verification of uniform torsional rigidity of square concrete-filled steel tubes [C]// Proceedings of the 25th National Conference on Structural Engineering. Baotou, 2016:465-468.

[28] 王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

Wang Xinmin. ANSYS engineering structure numerical analysis [M]. Beijing: China Communication Press, 2007.