考虑应力敏感效应的裂缝性复合油藏水平井压力动态分析

姜瑞忠， 黄 磊， 崔永正， 范海军， 刘亚楠， 王小果， 佟 颖

( 1. 中国石油大学(华东) 石油工程学院，山东 青岛 266555； 2. 中国石油天然气股份有限公司 北京油气调控中心，北京 100007； 3. 中国石油化工股份有限公司 石油工程研究院，北京 100101 )

0 引言

水平井比直井能更有效地开发裂缝性油气藏，在解析试井研究中，将裂缝性油气藏视为双重介质，将水平井简化为线源。王东权等[1]考虑有效井径的双重介质建立油藏试井模型，得到产量递减规律。李晓平等[2]采用拉氏变换法和叠加原理，推导无限大外边界和盒状封闭外边界双重介质油藏水平井压力动态解。邓英尔等[3]利用椭圆坐标系研究各向异性双重介质油藏，建立水平井开发两相流试井模型。Ng M C等[4]运用叠加原理推导封闭外边界裂缝性油藏的压力解。Nie R S等[5]考虑基质对井筒的供液，建立双孔双渗水平井渗流模型。Zhang W等[6]考虑页岩气的渗流特点和储层物性，建立针对页岩气藏的四重孔隙数值模型。王家航等[7]基于点源函数理论和边界元思想，建立非均质油藏多段压裂水平井非稳态压力分析的半解析模型。董文秀等[8]建立各向异性箱形储层中被部分射开直井的数学模型。史晓东[9-10]对非均质性致密油藏进行缝网压裂，建立产能预测模型。基于示踪剂返排曲线，李林凯等[11]运用时间矩理论，建立累计流动能力与累计储存能力图版评价裂缝网络。

人们对复合油藏水平井的渗流模型进行研究。王晓冬等[12]采用源汇叠加方法，建立复合油藏水平井的有效井径模型。石国新等[13]采用Laplace变换和分离变量法，建立均匀介质两区复合油藏水平井试井模型，进行相关实例验证。Ezulike O等[14]推导线性复合油藏水平井井底压力半解析解，分析非均质线性复合油藏中水平井的压力动态特征。姜瑞忠等[15]考虑水平井穿透复合油藏内区建立试井模型，求解内、外区点源解，将点源解沿水平井筒积分得到线源解。吴明录等[16]建立三重介质复合油藏水平井试井模型，对碳酸盐岩稠油热采进行试井分析。Zhang W等[17]考虑吸附和解吸建立复合煤层气藏水平井数学模型，分析复合煤层气藏中水平井生产动态特征。王海涛等[18]考虑页岩气解吸、扩散及内区非达西渗流和外区达西渗流，建立多重机制下的复合页岩气藏不稳定试井模型。

在双重介质油藏的不稳定试井分析中，考虑平面非均质性和裂缝应力敏感效应的水平井渗流模型极少。基于Warren-Root模型，笔者考虑基质向裂缝的拟稳态窜流和裂缝的应力敏感效应，建立天然裂缝性复合油藏的水平井渗流模型，为分析裂缝性复合油藏水平井压力动态提供指导。

1 物理模型

天然裂缝性复合油藏物理模型见图1，油藏被分为内、外两个区，平面上呈径向复合形态，内、外区由基质系统和天然裂缝系统构成。

假设条件：(1)油藏厚度为h，原始地层压力为pi；(2)内区半径为r1，外区无限大，储层顶面和底面封闭；(3)内、外区储层物性和流体性质不同，裂缝系统具有应力敏感效应；(4)内、外区流体微可压缩；(5)基于Warren-Root模型(见图2)，考虑基质与裂缝之间存在拟稳态窜流，流体由基质流向裂缝，再由裂缝流入井筒；(6)内区中间水平井视为线源，以定产量生产。

图1 裂缝性复合油藏物理模型

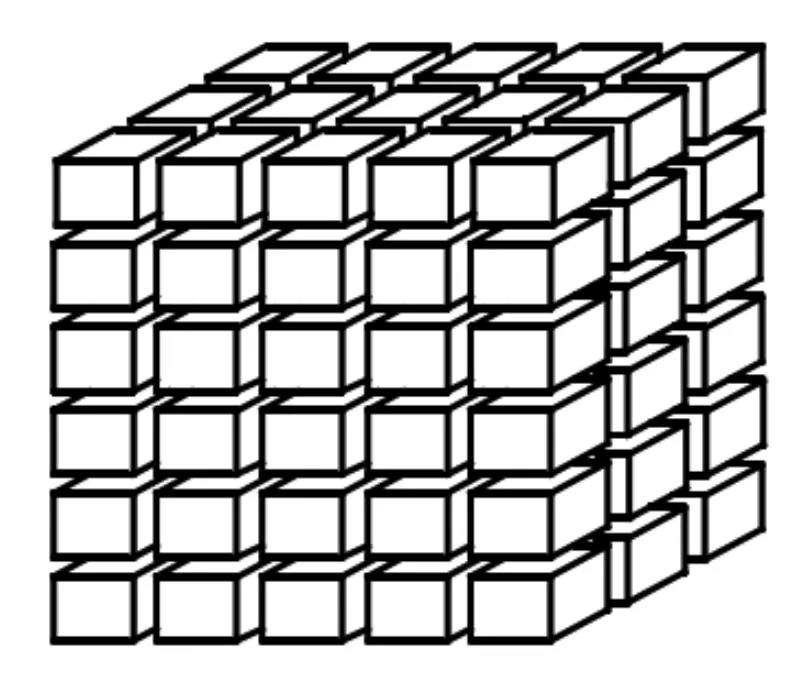
图2 Warren-Root模型示意Fig.2 Schematic diagram of Warren-Root model

2 数学模型

2.1 模型建立

引入量纲一的变量，得到裂缝性复合油藏的数学模型，变量定义见表1。其中，pmj为基质系统压力；pfj为裂缝系统压力；C为井筒储存系数；kmj为基质渗透率；kfhij为裂缝水平方向原始渗透率；kfvij为裂缝垂直方向原始渗透率；μj为原油黏度；φfj为裂缝系统孔隙度；Ctfj为裂缝系统压缩系数；φmj为基质系统的孔隙度；Ctmj为基质系统的压缩系数；t为时间；γ为渗透率模量；qsc为水平井产量；αj为形状因子；L为水平井半长；x、y、z为空间坐标；r为任意点到储层中心的径向距离；ε为垂向距离；j=1，2，1表示内区，2表示外区。

表1 变量定义

内区数学模型：

(1)

(2)

外区数学模型：

(3)

(4)

内边界条件为

(5)

侧向无限大外边界条件为

(6)

封闭外边界条件为

(7)

内、外区分界面条件为

pf1D(r1D,tD)=pf2D(r1D,tD),

(8)

(9)

针对裂缝系统，对裂缝压力进行代换得

(10)

式中：ξfjD为摄动变换函数，j=1，2。

利用摄动处理方法消除方程的非线性得

(11)

(12)

(13)

式中：ξfjDn为n阶摄动变换函数，n=0,1,2,…。

将式(11-13)代入内、外区数学模型及辅助方程，取0阶摄动，消除方程非线性，得到数学模型：

内区

(14)

外区

(15)

辅助方程

(16)

2.2 模型求解

对式(14-16)进行关于tD的Laplace变换，变换法则为

(17)

式中：s为Laplace变量。

对式(17)进行关于zD的有限Fourier余弦变换得

(18)

经过变换消除tD和zD得到齐次方程组，对窜流项方程整理合并得

(19)

式中：

(20)

式中：

(21)

(22)

(23)

(24)

根据修正的Bessel方程的性质，求得内区裂缝系统压力解为

(25)

(26)

式中：I0、I1分别为零阶和一阶第一类虚宗量贝塞尔函数；K0、K1分别为零阶和一阶第二类虚宗量贝塞尔函数。

将式(25)进行有限Fourier余弦逆变换，得到拉式空间下内区裂缝系统压力解为

(27)

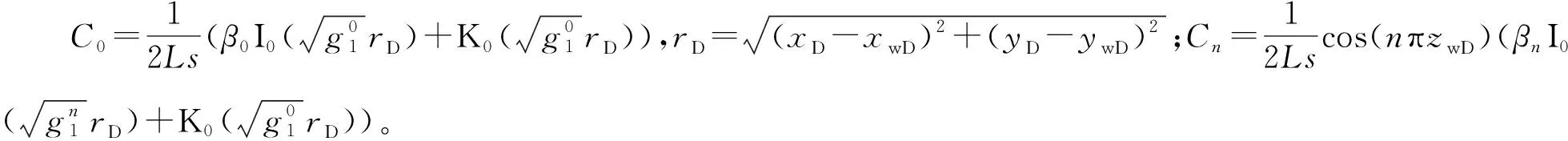
式(27)为双重介质复合油藏中的点源在内区的压力分布，点源解沿着水平井筒积分，得到双重介质复合油藏水平井井底压力解为

(28)

在拉式空间下，运用Duhamel原理并考虑井筒储集效应和表皮效应[19]，得到水平井无因次压力解为

(29)

式中：S为表皮因数。

采用Stehfest数值反演方法[20]，得到水平井压力动态解为

(30)

(31)

将式(10) 代入式(30)，得到考虑应力敏感效应的井底压力动态解为

(32)

3 模拟结果

3.1 典型曲线特征

采用数值积分和Stehfest数值反演方法，得到量纲一的压力及压力导数随量纲一的时间的变化关系(见图3)。初始参数为ω1=ω2=0.2，λ1=10-2，λ2=10-9，r1D=200，zwD=zD=0.25，CD=10-4，S=1。

根据曲线形态划分9个流动阶段：(1)井筒储存阶段，压力和压力导数曲线重叠呈斜率为1的直线；(2)早期过渡流阶段，受表皮因数的影响，压力导数曲线呈 “驼峰”状；(3)早期径向流阶段，主要受储层厚度的影响，流体垂直水平井筒径向流动，压力导数曲线表现为0.25L1D水平线；(4)线性流阶段，裂缝中的流体线性流向井筒，压力导数曲线表现出斜率为0.5的直线；(5)内区基质向裂缝窜流阶段，基质中的流体流向裂缝，压力导数曲线表现为“凹子”；(6)内区中期径向流阶段，内区流体在水平面上径向流向井筒，压力导数曲线表现为0.5水平线；(7)内区向外区过渡流阶段；(8)外区基质向裂缝窜流阶段，压力导数曲线表现为“凹子”；(9)晚期拟径向流阶段，由于存在应力敏感效应，压力导数曲线出现小幅度上翘。

3.2 参数敏感性分析

3.2.1 渗透率模量

渗透率模量对井底压力动态的影响见图3。由图3可以看出，由于天然裂缝存在应力敏感性，压力和压力导数曲线在晚期拟径向流阶段出现上翘，应力敏感性越强，后期上翘的幅度越大。随渗透率模量增大，裂缝渗透率减小，流体在储层中流动更困难，导致压降增大。

3.2.2 裂缝储容系数

内、外区裂缝储容系数对井底压力动态的影响见图4和图5。由图4可以看出，随内区裂缝储容系数增大，早期径向流持续时间增加，线性流阶段和内区基质向裂缝的窜流阶段出现延迟，窜流阶段的“凹子”最低点升高。内区储容系数越大，裂缝储容能力越强，裂缝中原始储存的流体流向井筒持续时间增加，基质储容能力下降，导致基质向裂缝的窜流量减小。由图5可以看出，随外区裂缝储容系数增大，内区向外区过渡流阶段持续时间增加，外区基质向裂缝的窜流阶段出现更晚，窜流阶段的“凹子”最低点升高。因此，储容系数决定窜流的时间和强度。

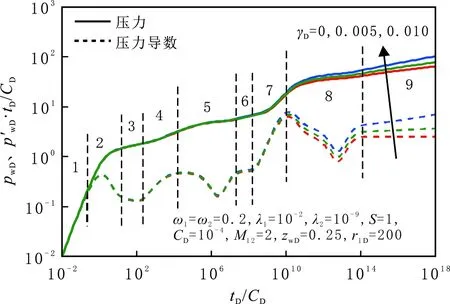
图3 渗透率模量对压力动态曲线的影响Fig.3 Effect of γD on pressure dynamic curves

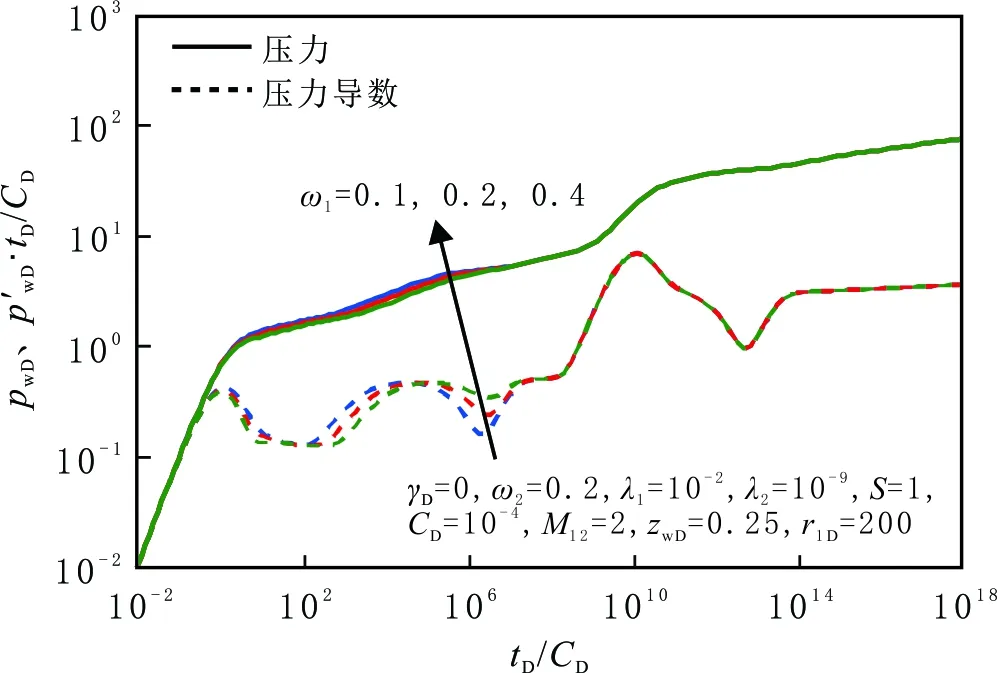
图4 内区储容系数对压力动态曲线的影响Fig.4 Effect of ω1 on pressure dynamic curves

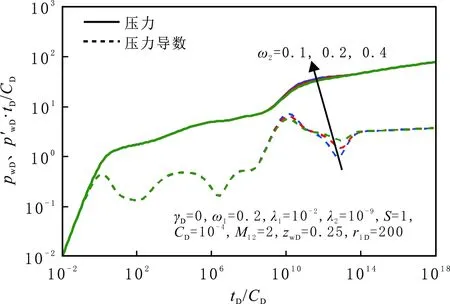
图5 外区储容系数对压力动态曲线的影响Fig.5 Effect of ω2 on pressure dynamic curves

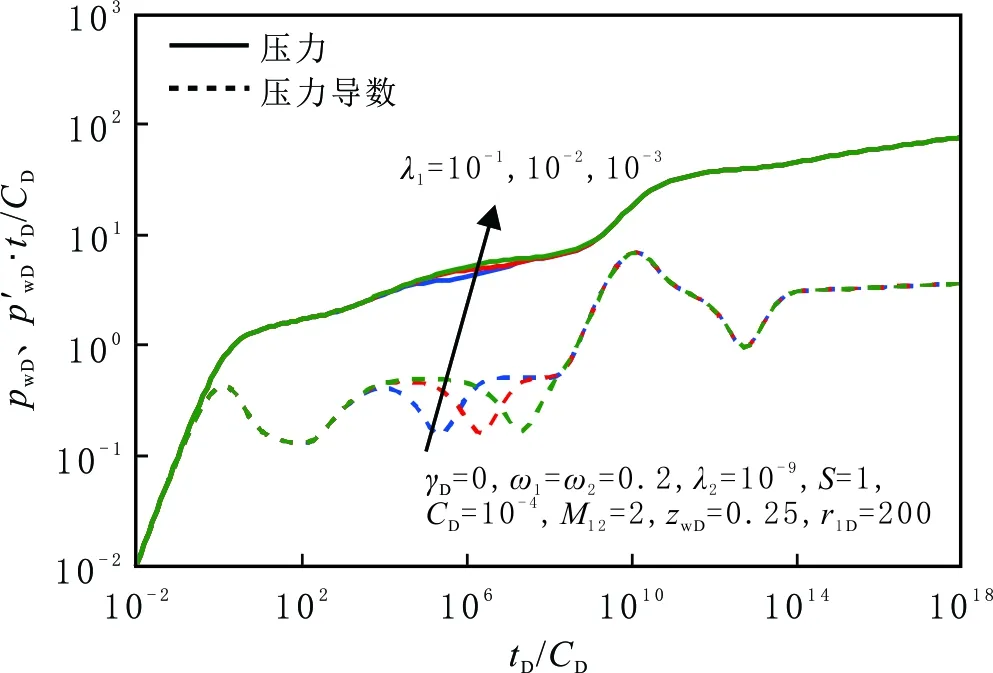
图6 内区窜流系数对压力动态曲线的影响Fig.6 Effect of λ1 on pressure dynamic curves

3.2.3 窜流系数

内、外区窜流系数对井底压力动态的影响见图6和图7。由图6可以看出，内区窜流系数主要影响内区基质向裂缝窜流阶段和内区中期径向流阶段，内区窜流系数越大，内区基质向裂缝的窜流阶段出现越早，中期径向流持续时间增加；内区窜流系数较小时，内区中期径向流阶段可能消失。由图7可以看出，外区窜流系数主要影响内区向外区过渡流阶段和外区基质向裂缝窜流阶段，外区窜流系数越大，外区基质向裂缝的窜流阶段出现越早，晚期拟径向流阶段出现延迟；窜流系数越小，基质向裂缝的窜流越困难，窜流阶段出现更晚，影响径向流阶段的出现。

3.2.4 内外区流度比

内外区流度比对井底压力动态的影响见图8。由图8可以看出，内外区流度比越大，内区渗流性质越好，外区渗流性质越差，外区流动需要更大的压差，导致压力和压力导数曲线上翘。随流度比增大，流体在外区流动更困难，内区向外区过渡流阶段持续更久，外区窜流阶段和晚期拟径向流阶段出现更晚。

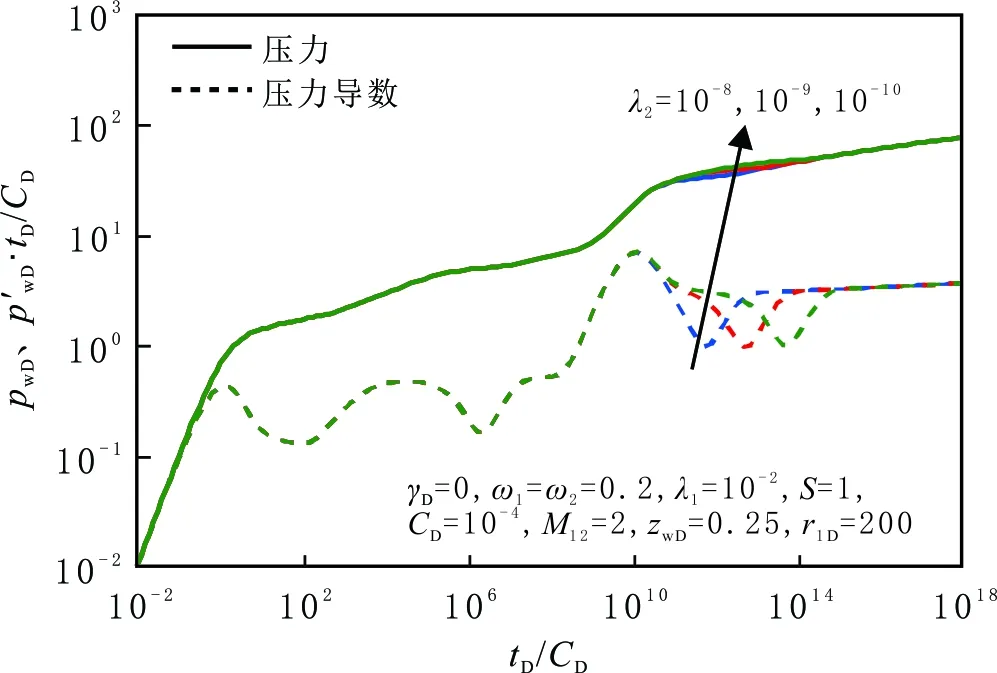
图7 外区窜流系数对压力动态曲线的影响Fig.7 Effect of λ2 on pressure dynamic curves

图8 内外区流度比对压力动态曲线的影响Fig.8 Effect of M12 on pressure dynamic curves

3.2.5 内区半径

内区半径对井底压力动态的影响见图9。由图9可以看出，内区半径主要影响中期径向流之后的流态，内区半径扩大使内区中期径向流的持续时间增加，压力波传到外区的时间延长，内区向外区过渡流阶段和外区基质向裂缝窜流阶段出现更晚。

3.2.6 水平井垂向位置

水平井垂向位置对井底压力动态的影响见图10。由图10可以看出，水平井垂向位置主要影响内区早期径向流阶段。早期径向流是垂直井筒平面的径向流，水平井越靠近储层中央，早期径向流流动半径越大，压力波传到边界的时间越晚，早期径向流阶段持续的时间越长。

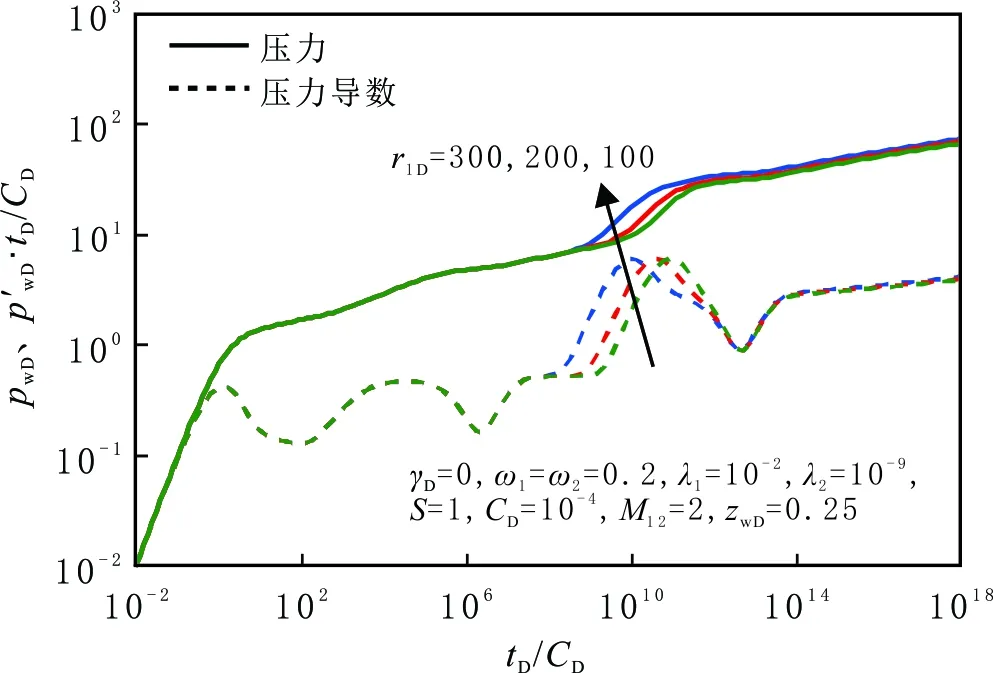
图9 内区半径对压力动态曲线的影响Fig.9 Effect of r1D on pressure dynamic curves

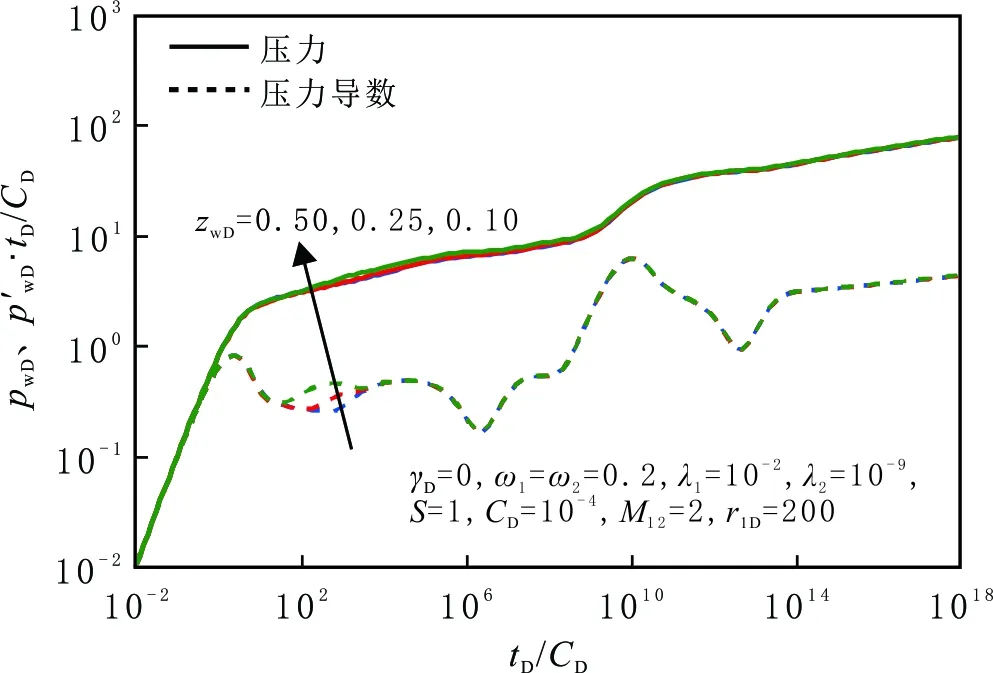
图10 水平井垂向位置对压力动态曲线的影响Fig.10 Effect of zwD on pressure dynamic curves

4 结论

(1)考虑基质向裂缝的拟稳态窜流、天然裂缝的应力敏感效应、井筒储集效应及表皮效应，建立裂缝性复合油藏的数学模型，运用Duhamel原理并采用有限Fourier余弦变换、摄动原理及Laplace变换等方法求解模型，得到内区点源解和线源解。

(2)采用Stehfest数值反演方法对模型求解，得到井底压力和压力导数曲线，划分9个流动阶段，分别为井筒储存阶段、早期过渡流阶段、早期径向流阶段、线性流阶段、内区基质向裂缝窜流阶段、内区中期径向流阶段、内区向外区过渡流阶段、外区基质向裂缝窜流阶段及晚期拟径向流阶段。

(3)应力敏感性越强，压力和压力导数曲线上翘幅度越大；裂缝储容系数越大，内、外区窜流阶段出现越早，窜流量越小，裂缝系统压降越大；窜流系数越大，窜流阶段出现越早；内外区流度比越大，内区向外区过渡流阶段持续越久，外区窜流阶段和晚期拟径向流阶段出现越晚；水平井垂向位置和内区半径分别影响早期径向流和中期径向流的持续时间。

参考文献(Reference)：

[1] 王东权,贾永禄,林涛,等.双重介质重整产量递减分析模型与应用研究[J].特种油气藏,2008,15(5):70-73.

Wang Dongquan, Jia Yonglu, Lin Tao, et al. Applied study of normalized and analytical model of production decline for dual-porosity reservoir [J]. Special Oil & Gas Reservoirs, 2008,15(5):70-73.

[2] 李晓平,沈燕来,刘启国,等.双重介质油藏水平井试井分析方法[J]. 西南石油大学学报:自然科学版,2001,23(5):16-18.

Li Xiaoping, Shen Yanlai, Liu Qiguo, et al. Analysis method of transient test for horizontal well in dual-porosity reservoir [J]. Journal of Southwest Petroleum Institute: Science & Techonlogy Edition , 2001,23(5):16-18.

[3] 邓英尔,刘慈群,刘树根.水平井开发渗透率各向异性双重介质油藏两相渗流[J].断块油气田,2002,9(5):37-39.

Deng Yinger, Liu Ciqun, Liu Shugen. Non-darcy flow of two-phase fluid through anisotropic doubleporosity media for horizontal well [J]. Fault-block Oil & Gas Field, 2002,9(5):37-39.

[4] Ng M C, Aguilera R. Well test analysis of horizontal wells in bounded naturally fractured reservoirs [J]. Journal of Canadian Petroleum Technology, 1994,38(7):20-24.

[5] Nie R S, Meng Y F, Jia Y L, et al. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir [J]. Transport in Porous Media, 2012,92(1):213-235.

[6] Zhang W, Xu J, Jiang R Z, et al. Employing a quad-porosity numerical model to analyze the productivity of shale gas reservoir [J]. Journal of Petroleum Science & Engineering, 2017,157:1033-1042.

[7] 王家航,王晓冬,董文秀,等.非均质油藏多段压裂水平井不稳态压力分析半解析方法[J].东北石油大学学报,2017,41(5):90-99.

Wang Jiahang, Wang Xiaodong, Dong Wenxiu, et al. Semi-analytical approach to model pressure of multiple-fractured horizontal wells in heterogeneous reservoirs [J]. Journal of Northeast Petroleum University, 2017,41(5):90-99.

[8] 董文秀,王晓冬,王家航.各向异性储层部分射开直井不稳态压力分析[J].东北石油大学学报,2017,41(6):96-104.

Dong Wenxiu, Wang Xiaodong, Wang Jiahang. Transient pressure analysis of partially penetrated vertical wells in anisotropic reservoirs [J]. Journal of Northeast Petroleum University, 2017,41(6):96-104.

[9] 史晓东.致密油直井多层缝网压裂产能预测方法[J].特种油气藏,2017,24(1):124-127.

Shi Xiaodong. Productivity forecast of vertical well with multi-layer network fracturing in tight oil reservoir [J]. Special Oil & Gas Reservoirs, 2017,24(1):124-127.

[10] 史晓东.非均质致密油储层水平井体积压裂产能预测[J].特种油气藏,2016,23(3):90-93.

Shi Xiaodong. Productivity forecast of volume-fractured horizontal well in heterogeneous tight oil reservoir [J]. Special Oil & Gas Reservoirs, 2016,23(3):90-93.

[11] 李林凯,姜汉桥,李俊键,等.基于示踪剂返排的致密油压裂缝网评价方法[J].特种油气藏,2017,24(5):102-106.

Li Linkai, Jiang Hanqiao, Li Junjian, et al. Techniques for assessments of hydraulic fracture network in tight oil reservoirs based on tracer discharging [J]. Special Oil & Gas Reservoirs, 2017,24(5):102-106.

[12] 王晓冬,刘慈群.复合油藏中水平井压力分析[J].石油学报,1997,18(2):72-77.

Wang Xiaodong, Liu Ciqun. Pressure analysis for horizontal wells in composite reservoirs [J]. Acta Petrolei Sinica, 1997,18(2):72-77.

[13] 石国新,聂仁仕,路建国,等.2区复合油藏水平井试井模型与实例解释[J].西南石油大学学报:自然科学版,2012,34(5):99-106.

Shi Guoxin, Nie Renshi, Lu Jianguo, et al. Well test model of horizontal well in 2-zoned composite reservoir and example interpretation [J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2012,34(5):99-106.

[14] Ezulike O, Igbokoyi A. Horizontal well pressure transient analysis in anisotropic composite reservoirs: A three dimensional semi-analytical approach [J]. Journal of Petroleum Science & Engineering, 2012,96-97(10):120-139.

[15] 姜瑞忠,孙召勃,王世朝,等.穿透内区的复合油藏水平井压力分析新方法[J].大庆石油地质与开发,2015,34(2):81-85.

Jiang Ruizhong, Sun Zhaobo, Wang Shichao, et al. Rate transient analysis for horizontal well passing through inner region of composite gas reservoir [J]. Petroleum Geology & Oilfield Development in Daqing, 2015,34(2):81-85.

[16] 吴明录,徐思南,丁明才,等.碳酸盐岩稠油热采水平井试井解释模型及压力动态特征[J].油气井测试,2017,26(4):1-6.

Wu Minglu, Xu Sinan, Ding Mingcai, et al. Well testing interpretation model and dynamic pressure characteristics of horizontal well heavy oil thermal recovery in carbonate reservoir [J]. Well Testing, 2017,26(4):1-6.

[17] Zhang W, Jiang R, Xu J, et al. Production performance analysis for horizontal wells in composite coal bed methane reservoir [J]. Energy Exploration & Exploitation, 2017,35(2):194-217.

[18] 王海涛,彭倩,张烈辉,等.考虑非达西渗流的复合页岩气藏试井模型[J].东北石油大学学报,2018,42(1):96-102.

Wang Haitao, Peng Qian, Zhang Liehui, et al. Well testing model for composite shale gas reservoir considering non-darcy percolation [J]. Journal of Northeast Petroleum University, 2018,42(1):96-102.

[19] Van-Everdingen A F, Hurst W. The application of the Laplace transformation to flow problem in reservoirs [J]. Journal of Petroleum Technology, 1949,1(12):305-324.

[20] Stehfest H. Algorithm 368: Numerical inversion of Laplace transforms [J]. Communications of the Acm, 1970,13(1):47-49.