考虑储层应力敏感效应的体积压裂水平井瞬态压力分析

李 准， 吴晓东， 韩国庆， 马高强， 张路锋， 王 彪

( 1. 中国石油大学(北京) 石油工程教育部重点实验室，北京 102249； 2. 中国石油大学( 北京) 非常规天然气研究院，北京 102200 )

0 引言

在油气田开发过程中，低渗特低渗储层开发普遍采用水平井大规模水力压裂技术，不仅可以产生较多的优势主渗流通道，还可以形成大型的缝网改造区(SRV)[1]。微地震数据显示，近井区域多次压裂的储层最小主应力方向发生明显变化，最终形成近似圆形压裂区域[1]。在开发过程中，致密储层的地层压力降低导致储层净覆压差增大，孔隙度、渗透率等物性随之降低[2]。在压裂改造过程中，地层经历复杂的地应力变化，人工裂缝与井筒并不一定是垂直的[2]。

人们在实验和理论方面研究致密油储层应力敏感效应，给出描述储层应力敏感效应的重要参数及方法，为高效合理开发低渗油藏提供基础[3-8]。Zhang M Y等[9]、Wang H等[10]、方思冬等[2]，Ren Z等[11]研究应力敏感储层的生产特征，但是没有考虑体积压裂改造区的影响。为研究压裂改造区对生产井产能和压力行为的影响，Ozkan E等[12-13]将“三线性流”的概念引入多段压裂水平井，验证“三线性流模型”的正确性。Stalgorova E等[14]建立多段压裂水平井“五区”线性模型，并考虑主裂缝周围SRV区域有限的情况。考虑低渗致密油气藏启动压力梯度和页岩气藏吸附、解吸等特性，姚军等[15]、苏玉亮等[16]、Brohi I G等[17]、姬靖皓等[18]等建立油气藏的“三区”和“五区”模型，分析压裂水平井的产量和压力的动态特征。这类“三区”和“五区”模型假定流体在不同区域内的流动遵循线性流规律，忽略体积压裂井的径向流阶段，同时假设主裂缝和水平井垂直[2]。Zhao Y L等[19]将储层体积压裂改造区简化为圆形区域，利用径向双区复合模型，研究改造区影响的致密储层的压力行为，给出不同边界条件下的带有SRV改造区的复合气藏的点源和线源解。Jiang R Z等[20]推导带有SRV改造区的致密油藏的点源和线源解，分析致密油藏体积压裂水平井的流动阶段和产量递减规律，以及内外区流度比、弹性储容比、内区半径等对不同流动阶段的影响，但是没有考虑储层的应力敏感效应。Zhao Y L等[21]利用相似方法，讨论内区(SRV)的应力敏感效应对页岩储层多级压裂水平井压力行为的影响，但是忽略外区储层的应力敏感效应，并假定主裂缝和井筒垂直。祝浪涛等[22]利用双区复合模型，研究体积压裂直井的渗流特征，并考虑内、外区的应力敏感性，模型是针对直井建立的，并没有推广到多级压裂水平井。这些模型忽略裂缝与井筒夹角对产能和压力行为的影响。

目前，还没有综合考虑改造区影响、储层应力敏感效应、井筒与裂缝夹角的压裂水平井的压力分析模型。笔者利用线源函数、摄动变换和拉普拉斯变换，建立考虑SRV改造区、储层应力敏感效应、裂缝和井筒夹角的体积压裂水平井的不稳定数学模型，绘制典型的压力曲线，进行流动阶段划分和重要参数的敏感性分析。

1 计算模型

1.1 物理模型

考虑改造区的体积压裂水平井的微地震数据见图1，物理模型见图2。基本假设条件：

(1)整个油藏被划分为两个区域(见图1-2)，内区为体积压裂改造区(SRV)，外区为未改造区，且外区储层为无限大地层；

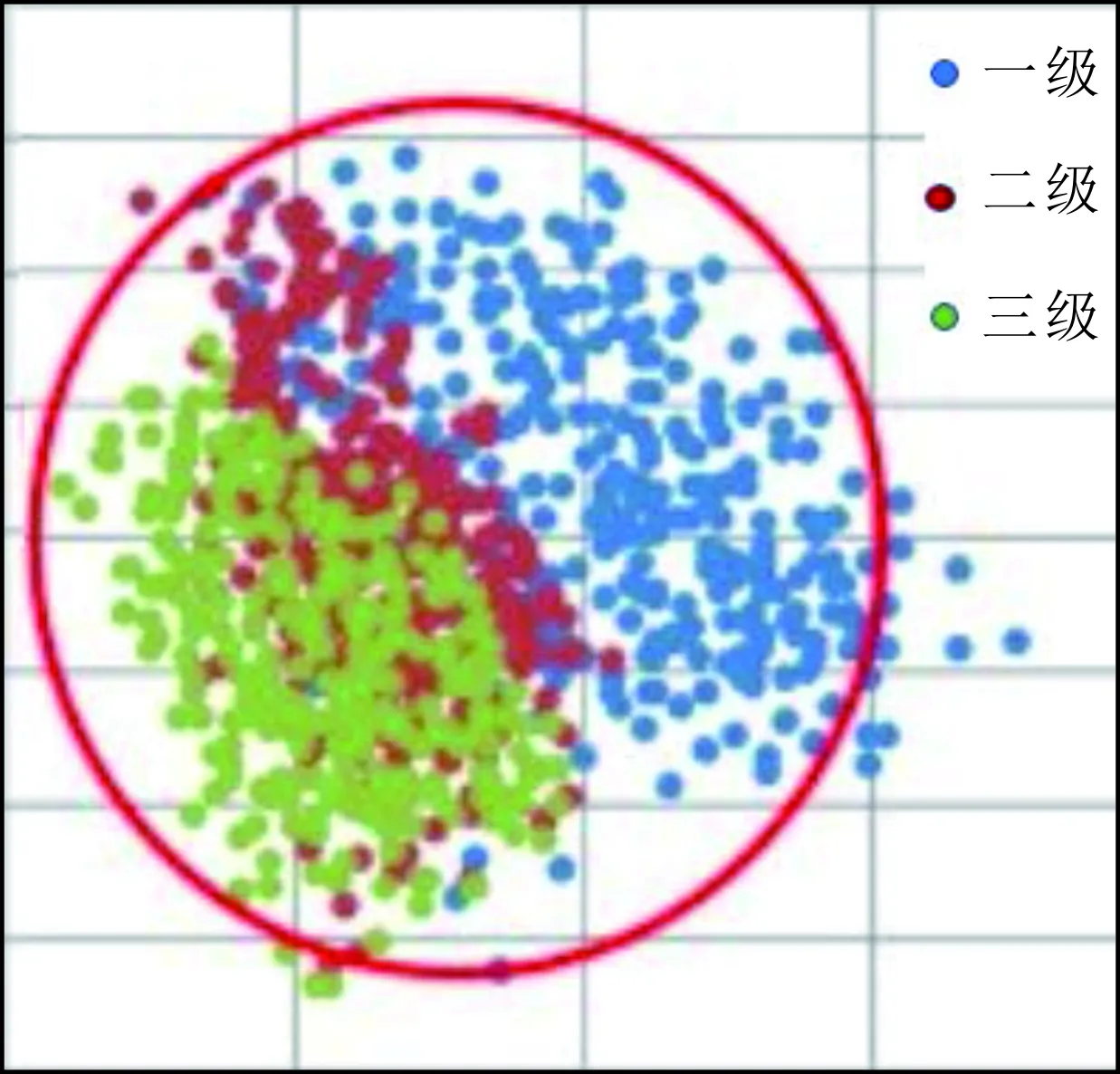
图1 微地震数据Fig.1 Microseismological diagram

图2 体积压裂水平井物理模型Fig.2 Physical model of volume-fractured horizontal well with SRV

(2)内、外区各为均质单重介质，受体积压裂等作业影响，内区和外区介质具有不同的初始渗透率、孔隙度和弹性压缩系数；

(3)内、外区多孔介质渗透率具有应力敏感效应，且内、外区的渗透率模量相同；

(4)内区存在多条与井筒呈一定角度的有效支撑倾斜裂缝，裂缝完全压开储层；

(5)内、外区流体简化为单相、均质微可压缩流体，流体遵循达西渗流原理；

(6)裂缝和井筒为无限导流，只在有裂缝的地方进行射孔，内区流体先流入裂缝，再由裂缝流入水平井井筒；

(7)渗流过程温度恒定，忽略重力和毛管力对渗流规律的影响。

1.2 数学模型

致密储层普遍存在应力敏感效应，常用的渗透率指数表达式为

K=Kie-γ(pi-p),

(1)

式中:Ki为初始渗透率；γ为渗透率应力敏感系数；pi为初始油藏压力。

考虑渗透率应力敏感效应的单相径向流的流动控制方程为

(2)

式中：Cl、Cr分别为流体和储层岩石的压缩系数；Ct为综合压缩系数；r为径向坐标；μ为原油黏度；φ为孔隙度。

因为γ≫Cl,γ≫Cr，可以忽略流体和储层岩石的压缩系数，引入量纲一的变量：

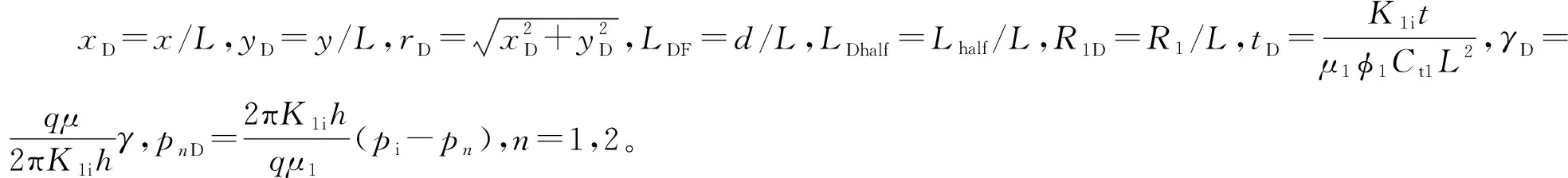
外区不稳定渗流方程为

(3)

边界条件

p2D|rD→∞=0。

初始条件

p2D(rD,0)=0。

内区不稳定渗流方程为

(4)

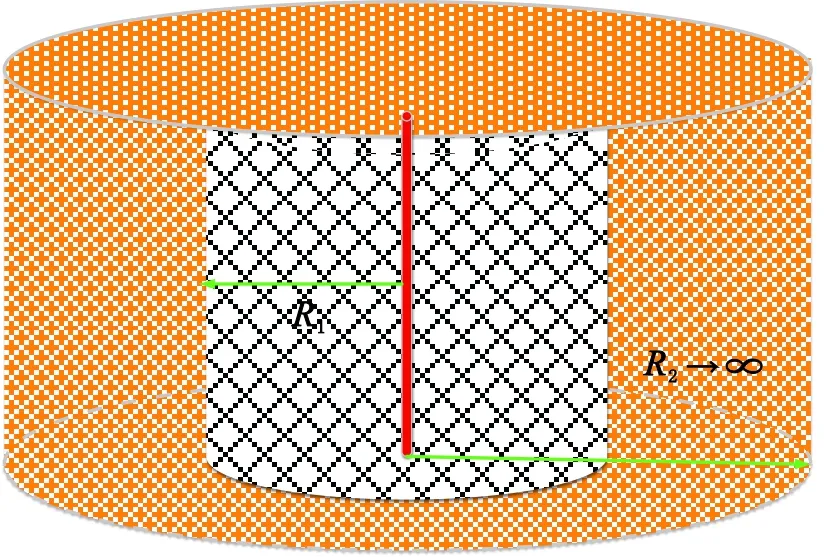
图3 复合油藏线源函数Fig.3 The schematic diagram of the line source in composite reservoir

根据δ(t)函数的性质，瞬时线源的内边界条件为

(5)

将等式左边写成无因次的形式：

(6)

内区初始条件

p1D(rD,0)=0。

内、外区衔接条件

p1D|rD=R1D=p2D|rD=R1D,

(7)

方程(3-4)为强非线性的偏微分方程，需要通过摄动变换求解[7]。引入新的量纲一的量ηjD:

(8)

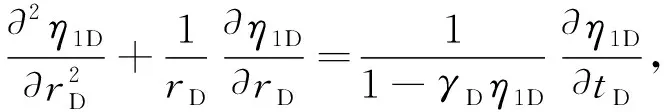
(9)

(10)

边界条件

(11)

η1D(rD,0)=η1D(rD,0)=0,

(12)

η1|rD=R1D=η2|rD=R1D,

(13)

(14)

(15)

根据Pedrosa O A等[7]提出的简化方法，对方程(9-10)和边界条件(11-15)分别取零阶摄动形式：

(16)

(17)

边界条件为

(18)

η1D0|rD=R1D=η2D0|rD=R1D,

(19)

(20)

(21)

利用拉氏变换得方程(16-17)的通解为

(22)

将边界条件(18-21)进行拉氏变换，并代入式(22)得：

(23)

(24)

(25)

式中：s为拉氏变量；Ki(x)、Ii(x)(i=0,1)分别为i阶虚宗量贝塞尔函数、i零阶贝塞尔函数；A1、B1、A2、B2为微分方程的通解系数。

(26)

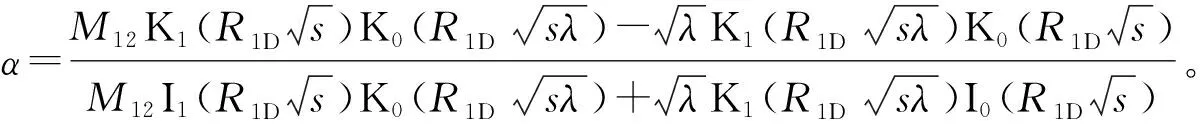
(27)

对式(27)进行拉氏变换得：

(28)

式(28)是双区复合油藏考虑内、外区应力敏感效应的连续线源解。假定线源位置的量纲一的坐标为(xlD,ylD)，则线源在量纲一坐标点(xD,yD)引起的压力响应公式可以写成一种更通用的形式[20]：

(29)

方程(16-17)为线性方程，零阶摄动解为线性解，满足叠加原理。对每一条裂缝进行离散(见图4)，假设裂缝条数为MF，第k条裂缝被划分为Nk个离散单元，所有裂缝离散单元的总数为N。根据叠加原理，所有裂缝离散单元对裂缝单元i中心点处的压力响应为

(30)

图4 裂缝离散单元

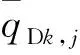
其中，θj为离散单元j与水井井筒夹角。

(31)

春小麦新品系丰产性及增产途径分析……………………………… 崔国惠，叶 君，吴晓华，王小兵，于美玲，付雅琼，李元清（1）

(32)

(33)

首先，在拉氏空间下求解式(33),得到井底压力的零阶摄动解；然后，运用Duhamel原理，得到考虑井筒存储效应CD和表皮效应S的拉氏空间下井底压力的零解摄动解[24]：

(34)

最后利用Stehfest数值反演法，求得真实空间下井底压力的零解摄动解[25-26]，并用式(8)变换得到井底压力pwD。

方思冬等[2]建立应力敏感储层多级倾斜裂缝水平井的压力分析模型，但是没有考虑近井地带改造区(SRV)和外区物性的差异。Jiang R Z等[20]建立考虑体积压裂改造区影响的多级压裂水平井的压力分析模型，但是没有考虑储层应力敏感效应、裂缝与井筒之间夹角对压力的影响。文中模型在内、外区储层物性取值相同的情况下，退化为方思冬等[2]建立的模型；将应力敏感因数取0，裂缝和井筒之间夹角取π/2时，退化为Jiang R Z等[20]建立的模型。

2 模型验证

为了验证文中模型的正确性，对比文中模型、文献[2]模型和文献[20]模型(见图5-6)。与文献[2]模型对比时参数：M12=ω12=1，LDF=200，LDhalf=100，裂缝条数MF=3，γD=0.1，水平井筒夹角θ=π/3，不考虑井筒存储效应和表皮效应的影响。与文献[20]模型对比时参数：M12=1.5，ω12=2，R1D=2 000，LDF=200，LDhalf=100，MF=3，θ=π/2，CD=100，S=0.1，不考虑应力敏感效应。由图5-6可以看出，文中模型的退化计算结果与文献[2]和文献[20]模型有较好的一致性。

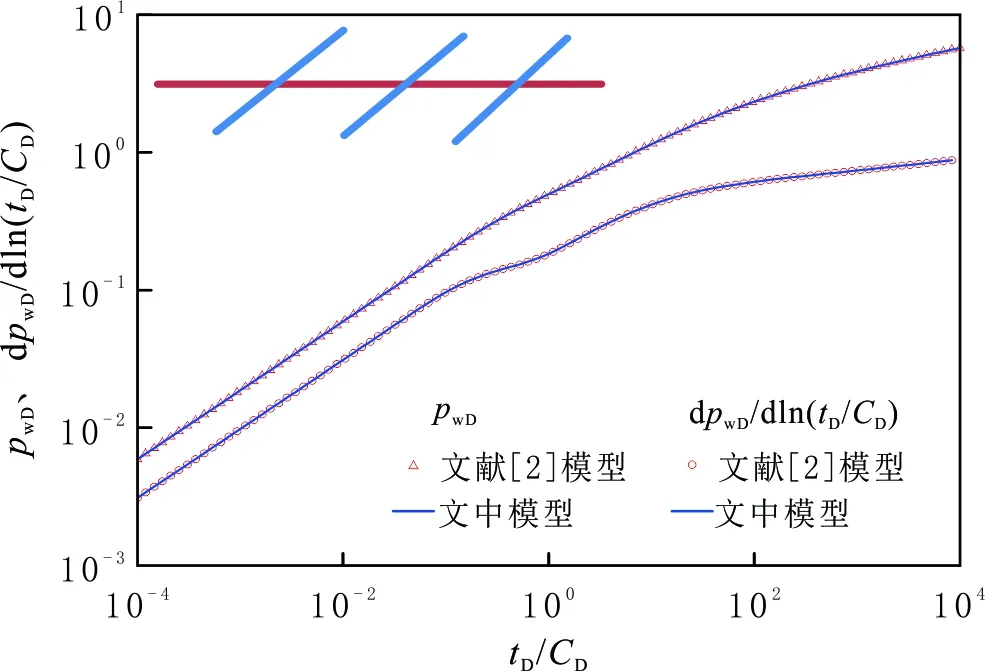
图5 文中模型与文献[2]模型结果Fig.5 Comparison between the model in this paper and that in Fang[2]

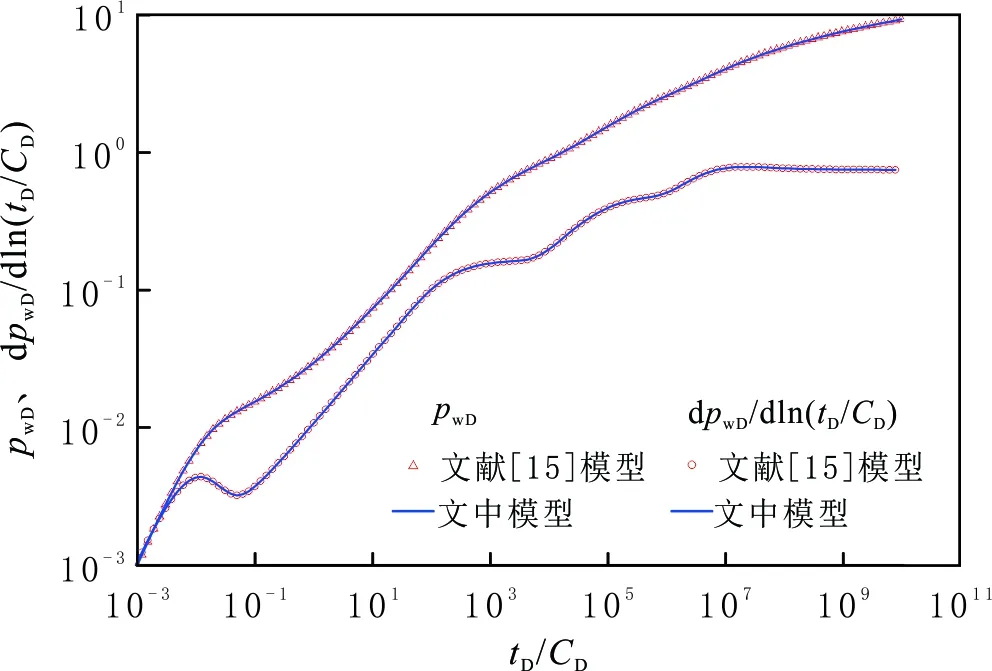
图6 文中模型和文献[20]模型结果Fig.6 Comparison between the model in this and that in Jiang R Z[20]

3 流动阶段划分

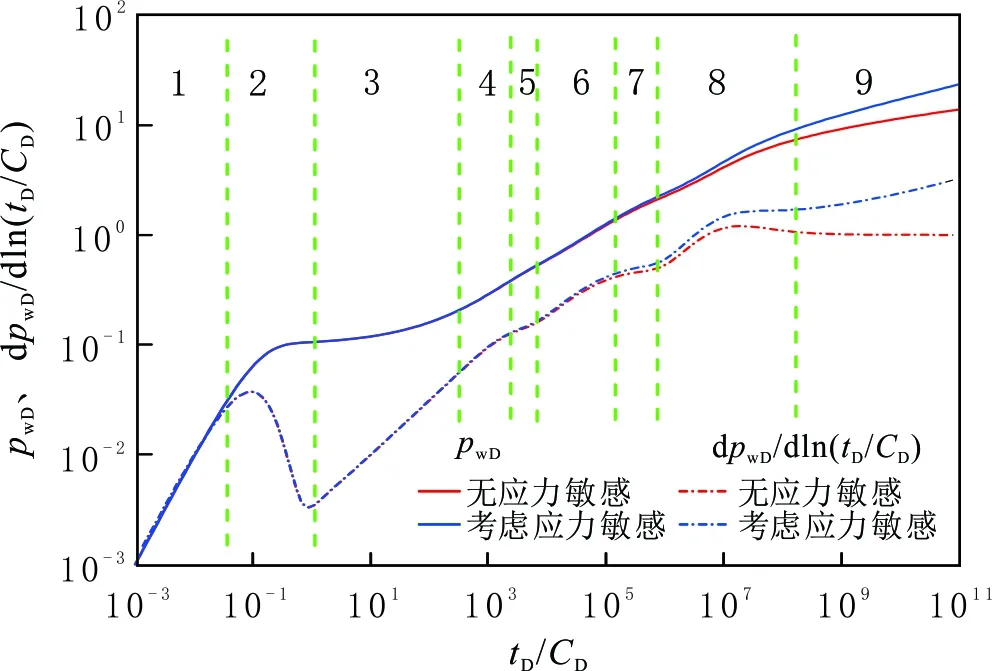
图7 应力敏感储层体积压裂水平井典型压力曲线响应Fig.7 Typical curve of pressure response for volume-fractured horizontal well in stress-sensitivity formation

当M12=1.5，ω12=2，R1D=2 000，LDF=200，LDhalf=100，MF=3，γD=0.05，θ=π/3，CD=100，S=0.1时，考虑改造区影响、应力敏感效应及裂缝和井筒夹角的压裂水平井的典型压力响应曲线，可以划分为9个流动阶段(见图7)。

第1阶段为井筒储集控制流，主要受井筒储集系数CD控制，表现为压力和压力导数曲线重合且斜率为1的直线。

第2阶段为井筒储集控制流向地层线性流的过渡阶段。压力导数曲线是一个向上凸起的驼峰，且驼峰大小受井筒储集系数和表皮因数共同控制。

第3阶段为内区地层线性流阶段(见图8(a))。受应力敏感效应影响很小，体积压裂改造区流体以垂直裂缝长度的方向流入裂缝，且各条裂缝之间没有相互干扰。典型特征是压力导数曲线的斜率为0.5。

第4阶段为内区地层线性流向内区早期径向流的过渡阶段。

第5阶段为内区早期径向流阶段(见图8(b))。应力敏感效应影响很小，裂缝之间没有相互干扰，有流体通过裂缝端部流入裂缝，在每条裂缝周围的流体以径向流的形式流入裂缝。典型特征是压力导数曲线的斜率为0。

第6阶段为内区双径向流阶段(见图8(c))。裂缝之间开始相互干扰，内区流体流向环绕水平井筒椭圆区域。

第7阶段为内区拟径向流阶段(见图8(d))。流体以径向流的方式流向井筒和裂缝区域，受内区应力敏感效应的影响，压力导数曲线斜率大于0.5。

第8阶段为内区拟径向流阶段向外区拟径向流的过渡阶段。压力逐渐由内区向外区扩散，压力导数曲线无明显特征。

第9阶段为外区拟径向流阶段(见图8(e))。外区流体以径向流的方式向内区流动，受应力敏感效应的影响较大，压力导数曲线值大于M12/2。

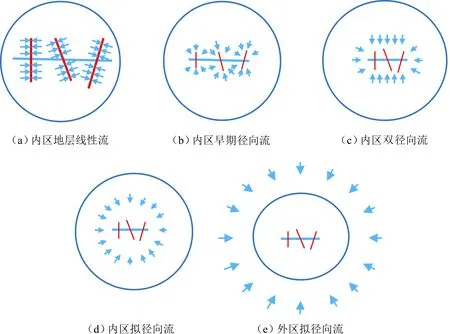
图8 体积压裂水平井流动阶段示意

4 敏感性分析

4.1 应力敏感因数

当M12=1.5，ω12=2，R1D=2 000，LDF=200，LDhalf=100，MF=3，θ=π/3，CD=100，S=0.1时，分别取γD为0.01、0.02、0.04、0.06时的压力动态曲线(见图9)。由图9可以看出，应力敏感因数越大，压力曲线上升越显著，且应力敏感效应对生产后期的影响明显大于前期的。受应力敏感效应的影响，内区径向流的压力导数曲线值高于0.5，外区径向流的压力导数曲线值大于M12/2，且应力敏感因数越大，压力导数曲线值越大。

当应力敏感因数增大到一定值时，压力导数曲线上升明显，表现类似封闭边界的特征。应力敏感因数越大，在单位压降下，裂缝和致密油储层的渗透率下降幅度越大，导致储层渗流能力下降幅度越大，破坏压裂井的开发效果。

4.2 改造区半径

当M12=1.5，ω12=2，γD=0.05，LDF=200，LDhalf=150，MF=3，θ=π/3，CD=100，S=0.1时，分别取R1D为1 000、1 500、2 000、2 500时的压力动态曲线(见图10)。由图10可以看出，改造区半径主要影响内区径向流的持续时间和结束时间，改造区半径越大，内区径向流持续时间越长，结束时间越晚。随改造区半径的增大，整个流动区域的“高渗”区域面积增大，整个致密油储层的渗流能力明显提升，致密储层得到有效开发。

4.3 改造效果

当R1D=2 000，ω12=2，γD=0.05，LDF=200，LDhalf=100，MF=3，θ=π/3，CD=100，S=0.1时，分别取M12为2、5、10时的压力动态曲线见图11。由图11可以看出，随M12增大,内区径向流结束时间变早，在相同的改造半径下，内区压力波传播速度变快。M12越大，即内区压裂改造效果越好，渗流能力越强，内区压力波传播速度越快，对采用衰竭式开采的致密油生产是有利的。

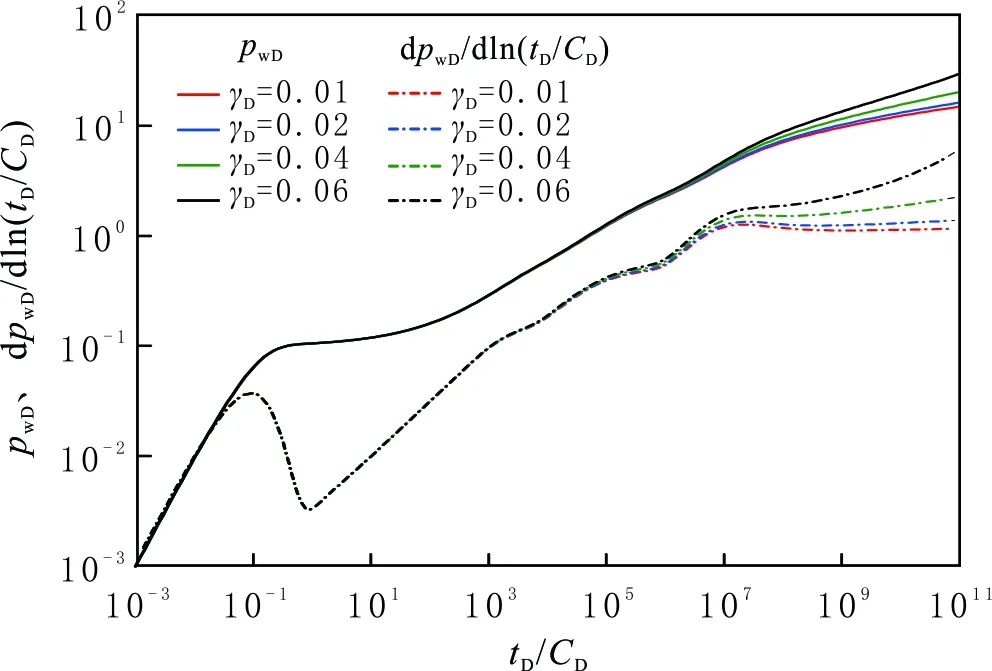
图9 应力敏感因数对压力动态的影响Fig.9 The effect of permeability stress sensitivity coefficient on pressure relationship

图10 改造区半径对压力动态的影响Fig.10 The effect of SRV radius on pressure relationship

4.4 裂缝与井筒夹角

当R1D=2 200，ω12=2，γD=0.02，LDF=200，LDhalf=100，MF=3，CD=100，S=0.1时，分别取θ为π/2、π/3、π/4、π/6、π/8时的压力动态曲线(见图12)(各条裂缝与井筒夹角相同)。由图12可以看出，当夹角在π/3～π/2之间时，裂缝与井筒夹角的变化对压力和压力导数曲线的影响很小。当夹角小于π/4时，裂缝与井筒夹角的改变对渗流规律的影响变得明显，主要影响内区线性流、内区双径向流及早期径向流阶段。裂缝与井筒夹角变小，裂缝之间水平间距变小，裂缝之间的干扰变强。在实际压裂施工中，应尽可能保持主缝与井筒垂直。

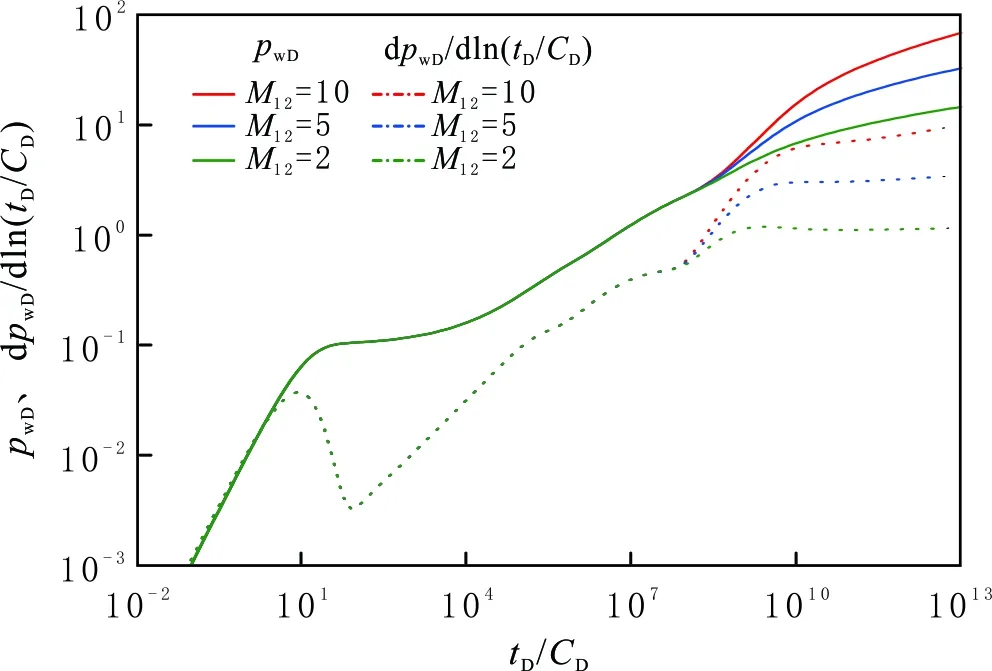
图11 内外区流度比压力动态的影响Fig.11 The effect of mobility ratio on pressure relationship

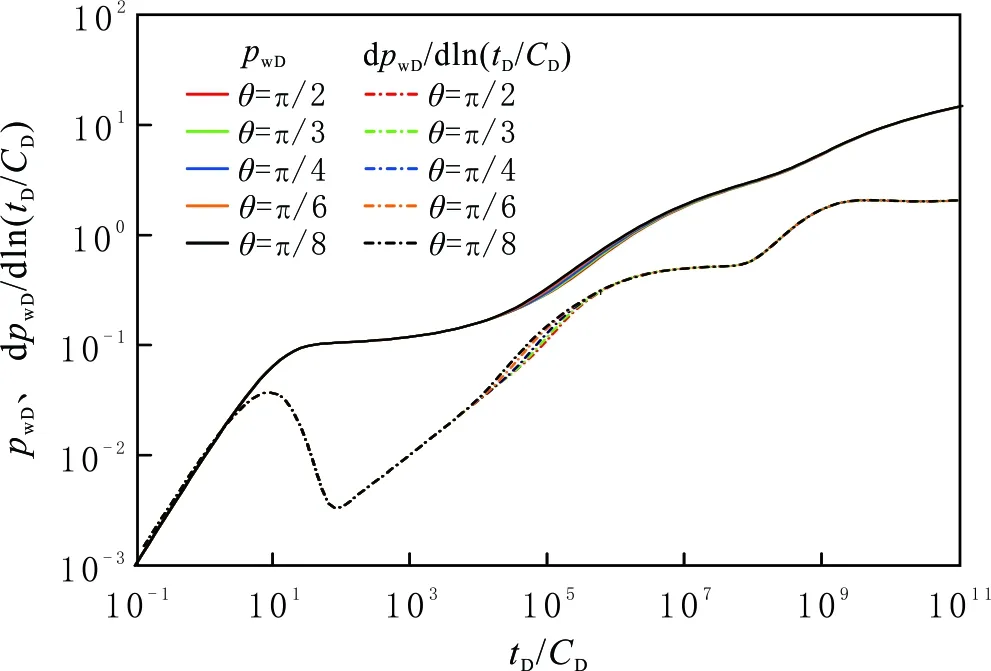
图12 裂缝与井筒夹角对压力动态的影响Fig.12 The effect of fracture dip on pressure relationship

4.5 裂缝长度

当R1D=2 200，ω12=2，γD=0.02，LDF=150，MF=3，CD=100，S=0.1，θ=π/3时，分别取LDhalf为70、100、120、150时的压力动态曲线(见图13)。由图13可以看出，裂缝长度主要影响内区线性流和内区双径向流，对其他阶段的影响较小。当LDhalf小于120时，随LDhalf增加，两个阶段的压力及压力导数明显降低；当LDhalf大于120时，压力和压力导数随裂缝长度的增加而降低的趋势变缓。说明增加裂缝长度即增加体积压裂井的泄油面积，降低总的渗流阻力，但在实际生产中考虑压裂成本，裂缝长度存在一个最优值。

4.6 裂缝间距

当R1D=2 200，ω12=2，γD=0.02，MF=3，CD=100，S=0.1，θ=π/3，LDhalf=100时，分别取LDF为100、150、200、250、300时的压力动态曲线(见图14)。由图14可以看出，裂缝间距主要影响内区双径向流和早期径向流阶段。当裂缝条数和长度一定时，裂缝间距的增大相当于泄油面积的增大，同时裂缝间距越大，裂缝之间的干扰越弱，整体渗流阻力也越小，因此压力和压力导数也越小。在其他参数一定时，增大裂缝间距对致密储层的生产更有利。

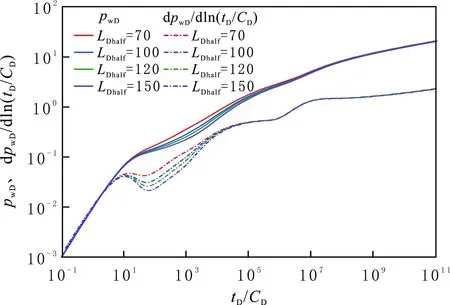
图13 裂缝长度对压力动态的影响Fig.13 The effect of fracture half length on pressure relationship

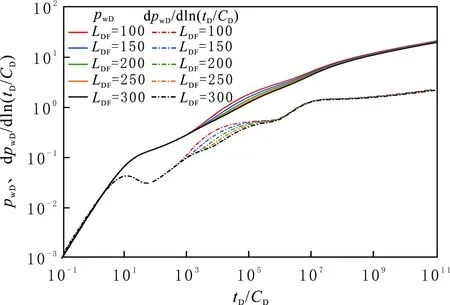
图14 裂缝间距对压力动态的影响Fig.14 The effect of fracture spacing on pressure relationship

4.7 裂缝条数

当R1D=2 200，ω12=2，γD=0.02，CD=100，S=0.1，θ=π/2，LDhalf=100，LDF=150时，分别取MF为3、5、8、10时的压力动态曲线(见图15)。由图15可以看出，裂缝条数几乎影响内区渗流的每一个阶段，并且随裂缝条数增加，内区渗流的各个阶段的压力和压力导数变小。在其他条件一定时，裂缝条数的增加既增加井与油藏的接触面积，也提高近井地带的渗流能力，是压裂增产的重要原因。

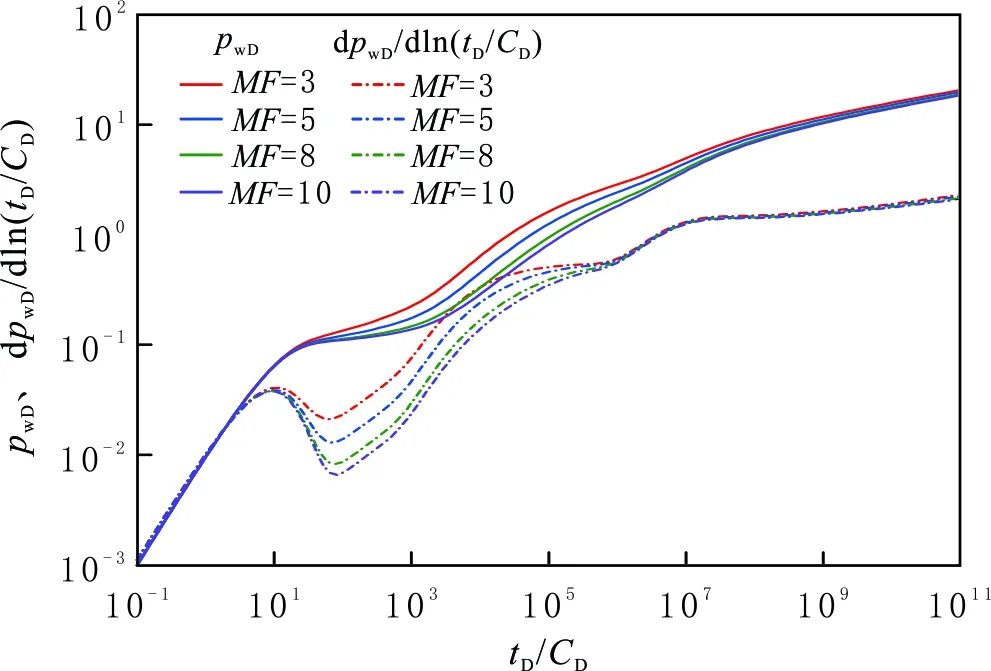
图15 裂缝条数对压力动态的影响

5 结论

(1)与常规的多级压裂水平井压力分析模型不同，文中模型综合考虑SRV改造区和未改造区储层物性的差异、内外区储层的应力敏感效应，以及裂缝倾角等对体积压裂水平井的压力动态的影响。文中模型退化结果与文献的模型具有较好的一致性。

(2)考虑改造区影响的体积压裂水平井的完整的渗流阶段划分为9个，分别为井筒储集控制流、井筒储集控制流向地层线性流的过渡流、内区地层线性流、内区地层线性流向内区早期径向流的过渡流、早期径向流、内区双径向流、内区拟径向流、内区拟径向流向外区拟径向流的过渡流，以及外区拟径向流。

(3)应力敏感效应对生产后期的影响更大，主要影响内区拟径向流、两区之间的过渡流及外区拟径向流。随应力敏感因数增大，压力和压力导数曲线变得更陡峭，应力敏感因数增大到一定程度时，压力响应表现出类似封闭边界的特征。

(4)裂缝倾角主要影响改造区的双径向流、内区早期径向流等阶段；裂缝间距主要影响内区地层双径向流和早期径向流阶段；裂缝长度主要影响内区地层线性流和双径向流阶段；裂缝条数对改造区的所有流动阶段有影响，明显降低内区各个渗流阶段的压力和压力导数。

参考文献(Reference):

[1] Zhao Y L, Zhang L H, Luo J X, et al. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir [J]. Journal of Hydrology, 2014,512(10):447-456.

[2] 方思冬,程林松,李彩云,等.应力敏感油藏多角度裂缝压裂水平井产量模型[J].东北石油大学学报,2015,39(1):87-94.

Fang Sidong, Cheng Linsong, Li Caiyun, et al. The productivity model of multi-angled fractured horizontal well in stress-sensitive reservoir [J]. Journal of Northeast Petroleum University, 2015,39(1):87-94.

[3] Fatt I, Davis D H. The reduction in permeability with overburden pressure [J]. Society of Petroleum Engineers, 1952,4(12):16.

[4] Mclatchie A S, Hemstock R A, Young J W. The effective compressibility of reservoir rock and its effects on permeability [J]. Journal Petroleum Technology, 1958,10(6):49-51.

[5] Gray D H, Fatt I. The effect of stress on permeability of sandstone cores [J]. Society of Petroleum Engineers Journal, 1963,3(2):95-100.

[6] Vairogs J, Rhoades V W. Pressure transient tests in formations having stress-sensitive permeability [J]. Journal of Petroleum Technology, 1973,25(8):965-970.

[7] Pedrosa O A. Pressure transient response in stress-sensitive formations [J]. SPE California Regional Meeting, 1986:203-210.

[8] 薛永超,程林松.不同级别渗透率岩心应力敏感实验对比研究[J].石油钻采工艺,2011,33(3):38-41.

Xue Yongchao, Cheng Linsong. Experimental comparison study on stress sensitivity of different permeability cores [J]. Oil Drilling & Production Technology, 2011,33(3):38-41.

[9] Zhang M Y, Ambastha A K. New insights in pressure-transient analysis for stress-sensitive reservoirs [C]∥SPE Annual Technical Conference and Exhibition. New Orleans, Louisiana, 1994:617-628.

[10] Wang H, Marongiu-Porcu M. Impact of shale gas apparent permeability on production: Combined effects of non-darcy flow/gas slippage, desorption, and geomechanics [J]. SPE Reservoir Evaluation & Engineering, 2015,18(4):495-507.

[11] Ren Z, Wu X, Han G, et al. Transient pressure behavior of multi-stage fractured horizontal wells in stress-sensitive tight oil reservoirs [J]. Journal of Petroleum Science & Engineering, 2017(157):1197-1208.

[12] Ozkan E, Raghavan R. New solutions for well-test analysis problems: Part Ⅰ-analytical considerations [J]. SPE Reservoir Evaluation & Engineering, 1991(a)63:59-68.

[13] Ozkan E, Raghavan R. New solutions for well-test analysis problems: Part Ⅱ-computational considerations and applications [J]. SPE Reservoir Evaluation & Engineering, 1991(b)63:69-78.

[14] Stalgorova E, Mattar L. Analytical model for history matching and forecasting production in multifrac-composite systems [C]∥Proceedings of the SPE Canadian Unconventional Resources Conference. View at Scopus, 2012:450-466.

[15] 姚军,殷修杏,樊冬艳,等.低渗透油藏的压裂水平井三线性流试井模型[J].油气井测试,2011,20(5):1-5.

Yao Jun, Yin Xiuxing, Fan Dongyan, et al. Tri-linear flow well test model of fractured horizontal well in low permeability reservoir [J]. Well Testing, 2011,20(5):1-5.

[16] 苏玉亮,王文东,盛广龙.体积压裂水平井复合流动模型[J].石油学报,2014,35(3):504-510.

Su Yuliang, Wang Wendong, Sheng Guanglong. Compound flow model of volume fractured horizontal we11 [J]. Acta Petrolei Sinica, 2014,35(3):504-510.

[17] Brohi I G, Pooladi-Darvish M, Aguilera R. Modeling fractured horizontal wells as dual porosity composite reservoirs application to tight gas, shale gas and tight oil cases [C]∥SPE Western North American Region Meeting. Alaska, USA, 2011.

[18] 姬靖皓,姚约东,马雄强,等.致密油藏体积压裂水平井不稳定压力分析[J].水动力学研究与进展(A辑),2017,32(4):491-501.

Ji Jinghao, Yao Yuedong, Ma Xiongqiang, et al. Pressure transient analysis for volume-fractured horizontal well in tight oil reservoirs Chinese [J]. Chinese Journal of Hydrodynamics(A),2017,32(4):491-501.

[19] Zhao Y L, Zhang L H, Luo J X, et al. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir [J]. Journal of Hydrology, 2014,512(10):447-456.

[20] Jiang R Z, Xu J, Sun Z B, et al. Rate transient analysis for multistage fractured horizontal well in tight oil reservoirs considering stimulated reservoir volume [J]. Mathematical Problems in Engineering, 2014,2014:1-11.

[21] Zhao Y L, Zhang L H, Liu Y H, et al. Transient pressure analysis of fractured well in bi-zonal gas reservoirs [J]. Journal of Hydrology, 2015,524(3):89-99.

[22] 祝浪涛,廖新维,赵晓亮,等.致密油藏直井体积压裂压力分析模型[J].大庆石油地质与开发,2017,36(6):146-153.

Zhu Langtao, Liao Xinwei, Zhao Xiaoliang, et al. Pressure analyzing model for the SRV vertical well in tight oil reservoirs [J]. Petroleum Geology & Oilfield Development in Daqing,2017,36(6):146-153.

[23] 王欢,廖新维,赵晓亮,等.超低渗透油藏分段多簇压裂水平井产能影响因素与渗流规律——以鄂尔多斯盆地长8超低渗透油藏为例[J].油气地质与采收率,2014,21(6):107-110.

Wang Huan, Liao Xinwei, Zhao Xiaoliang, et al. A study on productivity and flow regimes of segmented multi-cluster fractured horizontal well in ultra-low permeability reservoir-a case of Chang8 ultra-low permeability reservoir in Ordos basin [J]. Petroleum Geology and Recovery Efficiency, 2014,21(6):107-110.

[24] Van-Everdingen A F, Hurst W. The application of the Laplace transformation to flow problem in reservoirs [J]. Journal of Petroleum Technology, 1949,1(12):305-324.

[25] Chin L Y, Raghavan R, Thomas L K, et al. Fully coupled geomechanics and fluid-flow analysis of wells with stress-dependent permeability [J]. SPE Journal, 2000,5(1):32-45.

[26] 同登科,陈钦雷.关于Laplace数值反演Stehfest方法的一点注记[J].石油学报,2001,22(6):91-92.

Tong Dengke, Chen Qinlei. A note of Laplace numerical inversion for Stehfest method [J]. Acta Petrolei Sinica, 2001,22(6):91-92.