一种直流输电系统实时仿真的模型分割方法

刘 飞, 黄绍书, 郝正航, 陈 卓, 谈竹奎, 徐玉韬

(1. 贵州大学 电气工程学院, 贵州 贵阳 550025； 2. 贵州电网有限公司 电力科学研究院, 贵州 贵阳 550005)

与交流输电相比,高压直流输电具有输送容量大、送点距离远、电网互联方便、功率调节容易、线路走廊窄等诸多优点[1]。由于直流输电工程线路长、跨越地形复杂、故障率较高,所以直流输电线路保护的意义重大[2]。在直流输电的保护和控制系统的开发研究中,硬件在环(hardware-in-loop,HIL)仿真可以用来验证直流输电保护装置动作的正确性和控制策略的有效性等,有利于产品的研发。但是,所有基于HIL的研究都必须以实时仿真为前提。模型计算的复杂程度决定了仿真的速度,要想实现实时仿真,仿真硬件必须在一个步长内完成所有的计算任务。在硬件给定的情况下,能否实现实时仿真几乎由建模技术决定[3]。

模型分割方法是解决大电网实时仿真问题的有效手段之一。模型分割方法是基于分组分群的思想,将较大的系统分割成若干个子系统,将一个状态空间系统分为两个或多个状态空间群组,每个状态空间群组都对自己的状态空间矩阵进行计算,大大缩短了计算时间[4]。此外,基于分割模型的分核并行计算可以大大减轻一个处理器的计算负担,提高仿真规模。

文献[5-6]阐述基于RT-LAB平台实现大型风电系统和模块化多电平换流器的并行实时仿真,仿真结果与原模型基本一致。文献[7-8]采用模型分割方法将交直流电力系统进行并行计算,也大大加快了计算速度。但是,在交流部分进行模型分割时,会因模型分割产生单位延时而造成波形失真或结果错误,并且在交流部分进行分割时,整流器和逆变器都在一个CPU内计算,并没有减少运行在一个CPU内的开关数量,继而无法加速仿真。为此,本文提出在直流部分对模型进行分割,并将此方法应用于12脉波高压直流输电系统,通过仿真验证了所提分割方法的有效性。

1 接口算法

在直流部分对模型分割的好处是模型大幅度降阶,可以减少每个状态空间群组的开关数量和预计算量,节省仿真机的存储空间,加快仿真速度。分割后的接口算法是决定模型分割是否成功的关键因素。目前常采用的模型分割接口算法有:状态空间节点(SSN)算法、长输电线路解耦法、节点分裂法、阻尼阻抗法和理想变压器模型法等[4,9-12]。长输电线路解耦法只能在分布参数线路上进行分割,且波在线路上传输的时间必须大于仿真步长Δt；阻尼阻抗法在实现阻抗的实时匹配上难度较大；而理想变压器模型法实现起来最为简单,并且具有较高的精度,但需要在稳定性方面做一些改进。

1.1 理想变压器模型法

以图1所示的电路为例，进行理想变压器模型接口算法的理论分析,在虚线处将电路进行分割,左边网络称为子网1,右边网络称为子网2。基于替代定理,子网1侧用受控电流源等效子网2的电路,受控电流源电流等于测量得到的子网2电流i；子网2侧用受控电压源等效子网1的电路,受控电压源电压等于测量得到的子网1电压u。分割后的接口电路如图2。

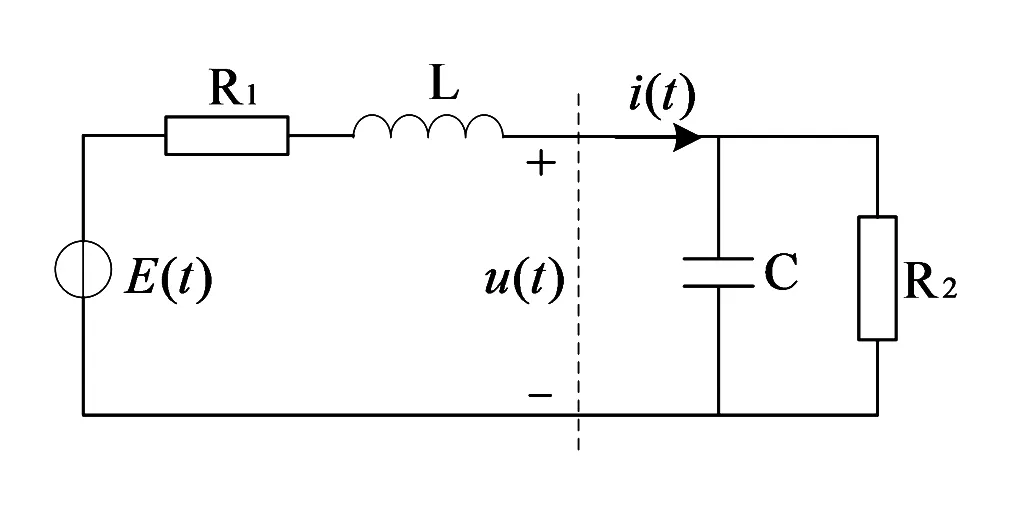
图1 典型电路

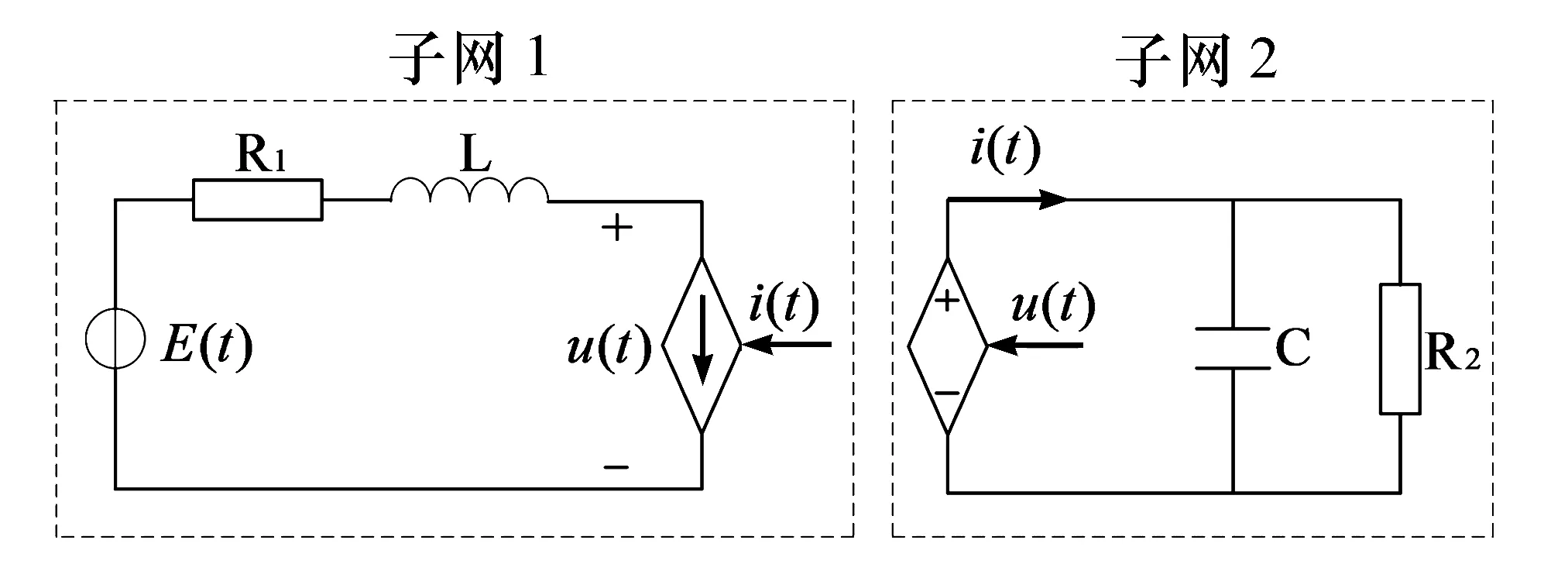
图2 理想变压器模型接口

采用理想变压器模型分割算法联立运行时仅需要子网的2个变量:(1)子网1的接口电压u,作为受控电压源的控制信号输入；(2)子网2的线路电流i,作为受控电流源的控制信号输入。由于受控电流源不能直接和电感元件串联,受控电压源不能直接和电容元件并联,所以需要对其进行差分处理。

采用隐式梯形积分法可得电感伏安特性的差分方程为[13]:

(1)

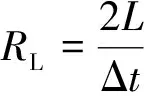
IL(t-Δt)=ikm(t-Δt)+

同理，可得电容伏安特性的差分方程为:

(2)

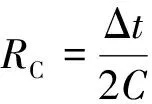
IC(t-Δt)=-ikm(t-Δt)+

差分化处理后计算电路如图3所示。

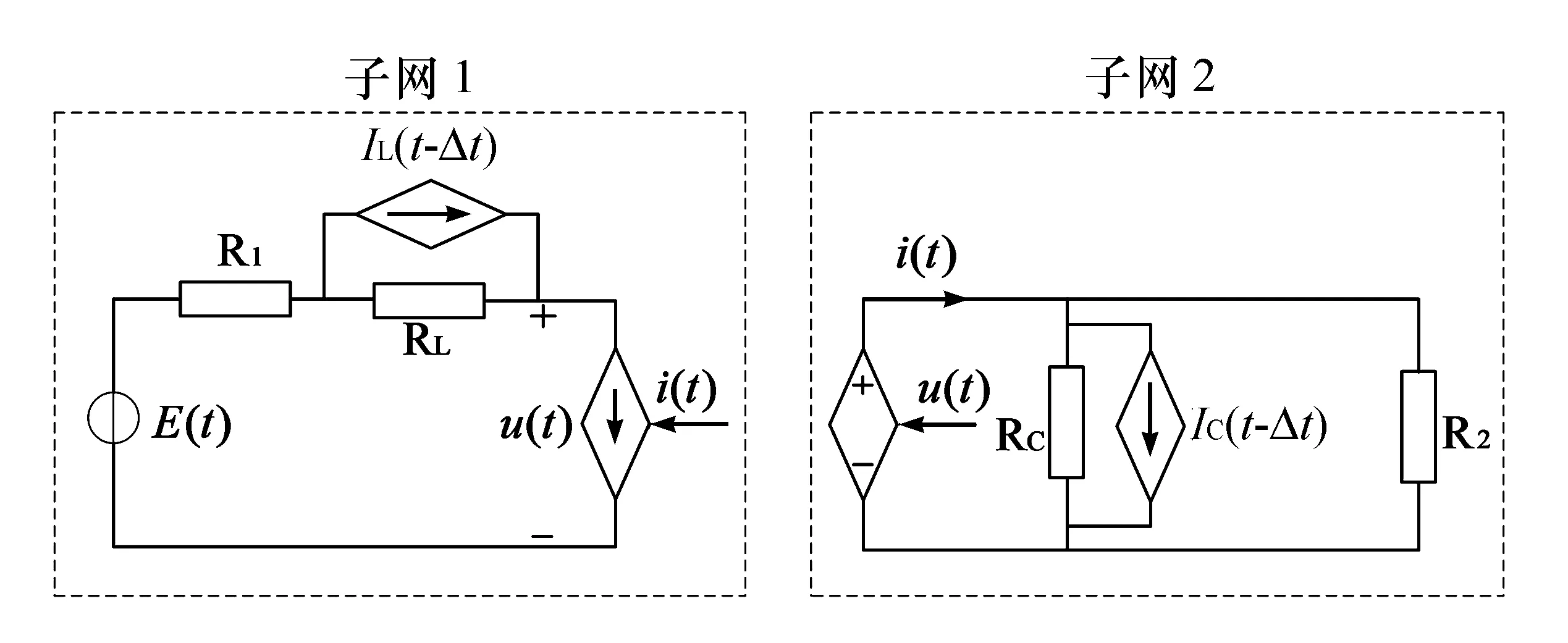
图3 差分化处理后计算电路

1.2 理想变压器模型法执行步骤

1.2.1 串行时序执行步骤

当采用串行计算对分割模型进行实时仿真时,为了避免两个子系统之间的状态空间方程出现代数环,需要选择子网2的线路电流i或子网1的接口电压u中的任意一项来设置延时环节。假设选择电压信号设置延时环节,则对串行仿真而言,子网2使用子网1上一步长的电压值,子网1直接使用子网2当前步长的电流值。分割后的系统串行计算执行时序如图4所示。

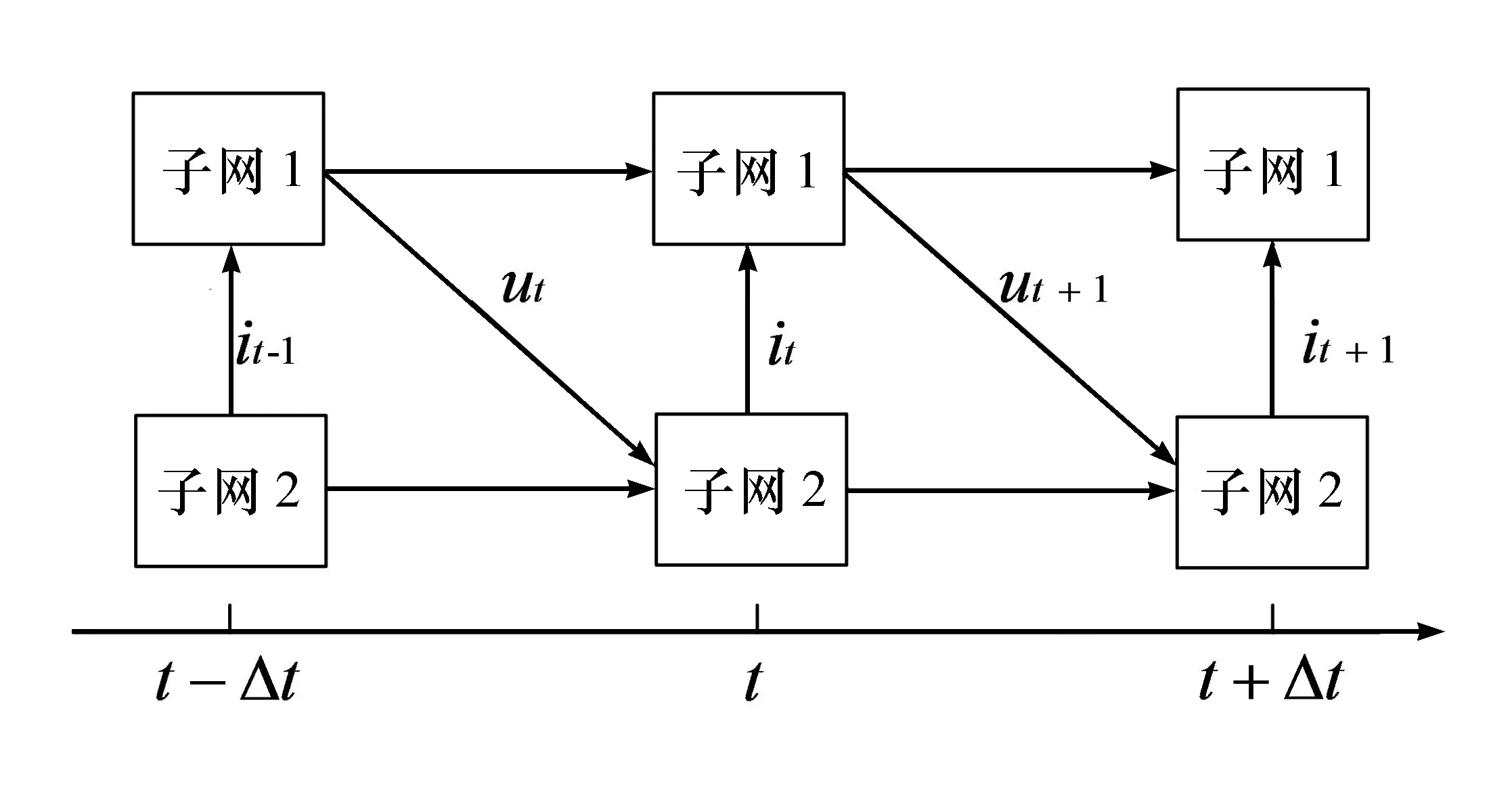
图4 串行计算执行时序

1.2.2 并行时序执行步骤

即使模型分割对原系统进行了大幅降阶和解耦,但是当采用串行计算时,所有网络方程的求解仍由一个CPU承担。当网络较大时,需要很大的存储量和预计算量,所以实时仿真的规模受到了很大的限制。

可以采用多核并行计算来扩大系统的仿真规模。将子网1下载到CPU1内进行实时仿真,子网2下载到CPU2内进行实时仿真。但在多核并行仿真上,CPU与CPU之间存在一个步长的固定延时,即子网1使用的是子网2上一步长的电流值,子网2使用的是子网1上一步长的电压值。分割后的系统并行计算时序如图5所示[14]。

对于交流信号而言,联解信号的延时问题会带来仿真误差。当新误差大于历史误差时,随着仿真的进行,可能会出现波形失真的现象。但在直流线路上进行模型分割时,由于直流电压和直流电流的特殊性,联解信号的延时对仿真基本无影响。

2 模型分割在直流输电系统中的应用

为验证理想变压器模型法的快速性和有效性,将接口算法应用于12脉波高压直流输电系统。

图6为进行仿真研究的高压直流输电系统。系统中,整流器采用电流控制,逆变器采用电压电流控制,将直流电压反馈给控制器控制触发脉冲。当直流侧发生故障时改变触发角,从而限制短路电流对晶闸管的冲击。其中系统1电压等级为500 kV、频率为60 Hz,通过整流器、直流线路及逆变器接到330 kV、50 Hz的系统2。为模拟控制系统的限流保护功能,模型中加入故障注入模块。

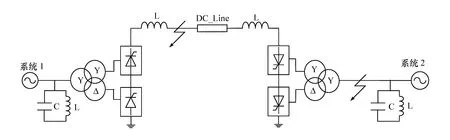
图6 高压直流输电系统

仿真中采用直流单极输电模式,整流器和逆变器采用同样的结构,分上下两个桥臂,则模型中所包含的开关器件总数将达到24个。

情形1:不对模型做任何处理,作为一个状态空间节点进行解算[5]：

x(t+Δt)=Akx(t)+Bky(t+Δt),k=1,2,…

(3)

在进行实时仿真时,实时仿真器会对每种开关状态进行预计算并且存储预计算所得到的系统矩阵,则k的取值将达到224=16 777 216个,这需要实时仿真器巨大的存储空间和计算量,可能导致实时仿真器无法在一个步长内完成所有的计算,最终不能对模型进行实时仿真。

情形2:将图6所示模型在直流线路上分割,作为2个状态空间群组进行串行计算,则其计算如式(4)—式(7)所示。

x1(t+Δt)=Ak1x1(t)+Bk1y1(t+Δt),

k1=1,2,…,212

(4)

x2(t+Δt)=Ak2x2(t)+Bk2y2(t+Δt),

k2=1,2,…,212

(5)

u1(t+Δt)=E1(t+Δt)-Z1i2(t+Δt)

(6)

u1(t)=E2(t+Δt)+Z2i2(t+Δt)

(7)

式(4)和式(5)分别表示群组1和群组2的状态空间,因为在群组1和群组2中分别只有12个开关,所以其系统矩阵预计算个数仅为212=4 096个,将两个群组放在一个CPU内进行串行计算,则CPU内需要预计算的系统矩阵个数为2·212=8 192。与情形1相比,显然节省了很大的存储空间和预计算量,同时大大减少了1个CPU的运算量,提高了运算速度,容易满足实时性的要求。

情形3:将图6所示模型在直流输电线路上分割,作为两个状态空间群组进行分核并行计算,则其计算如式(8)—式(11)所示。

x1(t+Δt)=Ak1x1(t)+Bk1y1(t+Δt),

k1=1,2,…,212

(8)

x2(t+Δt)=Ak2x2(t)+Bk2y2(t+Δt),

k2=1,2,…,212

(9)

u1(t+Δt)=E1(t+Δt)-Z1i2(t)

(10)

u1(t)=E2(t+Δt)+Z2i2(t+Δt)

(11)

式(10)表示在CPU1内进行的仿真计算表达式,式(11)表示在CPU2内进行的仿真计算表达式。两个群组分别在不同的核上进行计算,则系统矩阵预计算个数为212=4 096。这更加减少了1个CPU运算时的负担,同是也扩大了仿真规模。和串行计算相比,更容易满足实时化的要求。

3 仿真分析

为对比原模型和分割模型的仿真精度,进行了原模型和分割模型的暂态仿真。限于篇幅,这里只列出了并行计算的仿真结果。

设t=0.5 s时,在直流线路首端发生接地故障,t=0.6 s时故障消失；t=1 s时,在逆变器换流变压器出口处发生三相接地故障,t=1.1 s时故障消失。比较使用模型分割算法和不使用该算法下直流线路首端电压和电流、逆变器和整流器换流变压器出口处A相电压和电流,如图7—图12所示。

图7 直流线路首端电压Ud

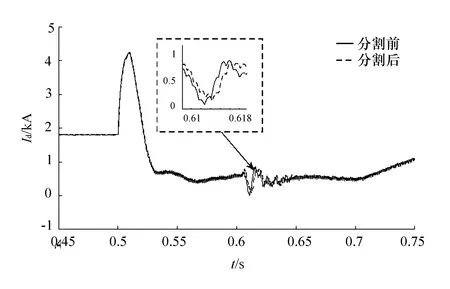
图8 直流线路首端电流Id

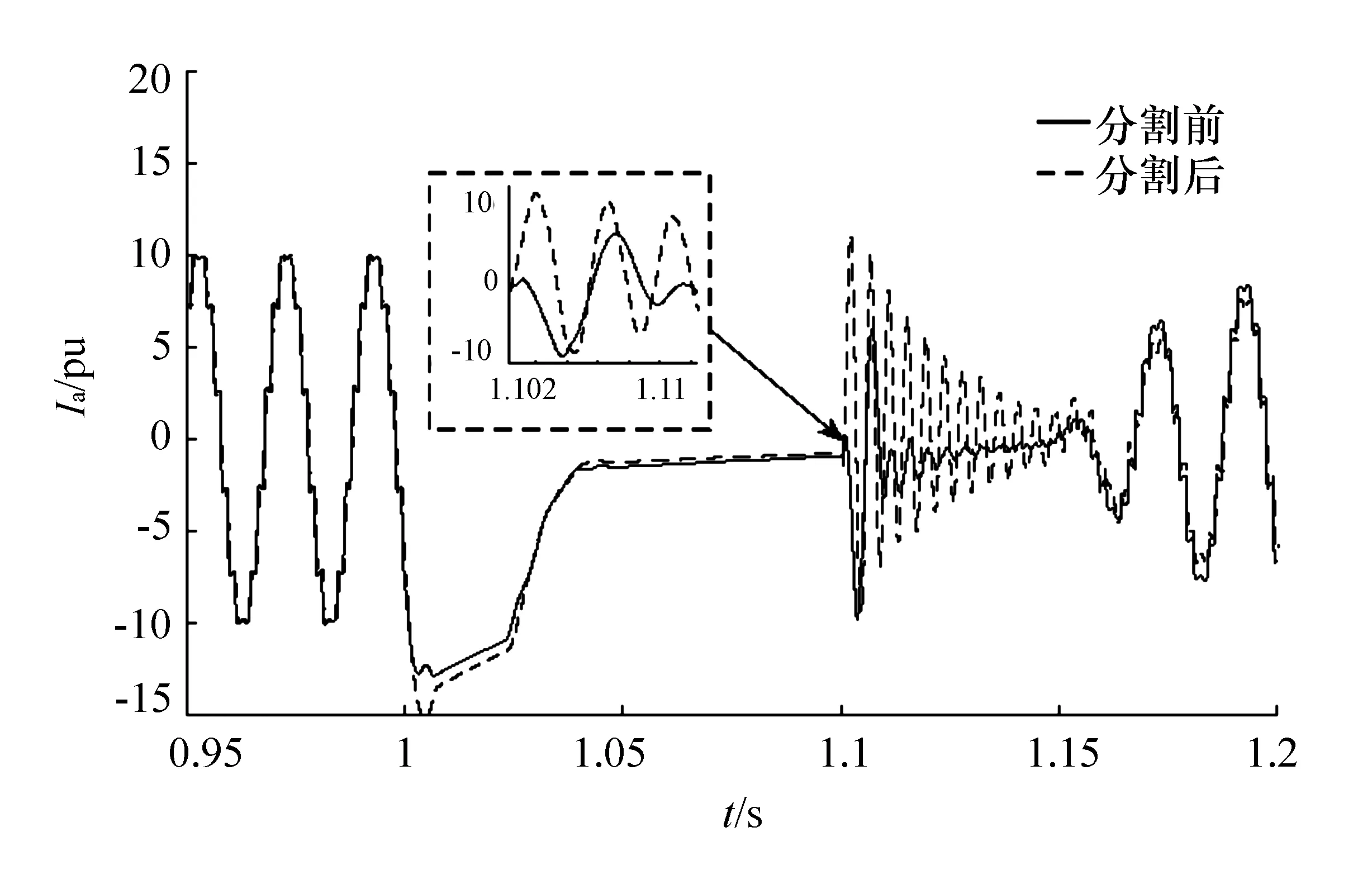
图9 逆变器换流变压器出口A相电流

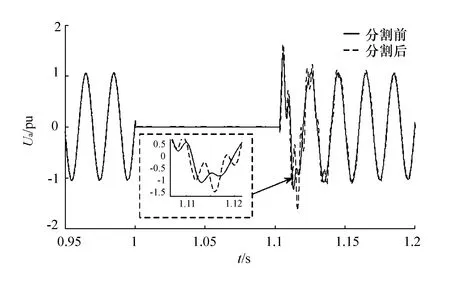
图10 逆变器换流变压器出口A相电压

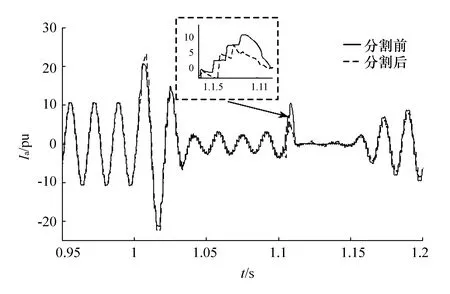
图11 整流器换流变压器出口A相电流

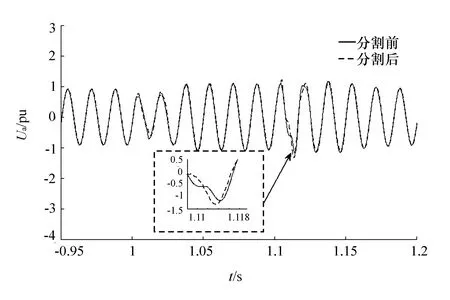
图12 整流器换流变压器出口A相电压

由仿真结果可知,采用模型分割算法所得的结果与没有采用该算法的结果在稳态情况下基本一致,仅仅是暂态情况下的精度有一些偏差,但波形的走势是一致的。主要原因是:在进行并行计算时,当发生故障以后,联解信号会发生突变,接口延时作用于突变信号上会对仿真精度产生一定的影响。

4 结语

在高压直流输电系统实时仿真中,需要占用实时仿真机大量的存储空间和预计算量,这可能导致仿真机无法对系统进行实时化仿真。采用理想变压器模型法,通过在直流线路上将一个大系统分割为两个群组,从而对系统进行解耦和大幅降阶,有效地减少了仿真机的存储空间和预计算量,提高了仿真速度。仿真结果表明,暂态过程中原模型和分割模型基本一致,仅仅是在有扰动的情况下,仿真精度会有一定的误差。

仿真实验表明,本文提出的模型分割方案是可行的,稳态和暂态仿真精度较好。该接口算法还有进一步优化的空间,特别是在严重扰动情况下,需要解决分割模型中的接口延时问题,进一步提高接口算法的精确度。

[1] 宋国兵,高淑萍,蔡新雷,等.高压直流输电线路继电保护技术综述[J].电力系统自动化,2012,36(22):123-129.

[2] 邢鲁华,陈青,高湛军.基于电压和电流突变量方向的高压直流输电线路保护原理[J].电力系统自动化,2013,37(6):107-112.

[3] 张宏俊,郝正航,陈卓,等.适用于模块化多电平换流器的实时仿真的建模方法[J].电力系统自动化,2017,41(7):120-126.

[4] Dufour C,Mahseredjian J,Belanger J.A combined state-space nodal method for the simulation of power system transients[J].IEEE Trans on Power Delivery,2011,26(2):928-935.

[5] 谭伟,邱华静,邹毅军.SSN算法在大型风电系统实时仿真中的应用[J].电力系统保护与控制,2014,42(5):98-103.

[6] 熊岩,赵成勇,刘启建,等.模块化多电平换流器实时仿真建模与硬件在环实验[J].电力系统自动化,2016,40(21):84-89.

[7] 田芳,周孝信.交直流电力系统分割并行电磁暂态数字仿真方法[J].中国电机工程学报,2011,31(22):1-7.

[8] 欧开健,胡云,梁旭,等.电磁机电混合实时仿真平台实用化技术研发与实现:(一)混合实时仿真数字量接口[J].南方电网技术,2013,7(6):1-6.

[9] 岳程燕,周孝信,李若梅.电力系统电磁暂态实时仿真中并行算法的研究[J].中国电机工程学报,2004,24(12):1-7.

[10] 岳程燕,田芳,周孝信,等.电力系统电磁暂态-机电暂态混合仿真接口实现[J].电网技术,2006,30(4):6-10.

[11] 李国庆,江守其,辛业春,等.柔性高压直流输电系统数字物理混合仿真功率接口及其算法[J].中国电机工程学报,2016,36(7):1915-1924.

[12] 陈磊,闵勇,叶俊,等.数字物理混合仿真系统的建模及理论分析:(一)系统结构与模型[J].电力系统自动化,2009,33(23):9-13.

[13] Dommel H W.电力系统电磁暂态计算理论[M].李永庄,译.北京:水利电力出版社,1991.

[14] 熊伟,夏文龙,余晓鸿,等.多核并行计算技术在电力系统短路计算中的应用[J].电力系统自动化,2011,35(8):49-52.