金属材料拉扭破坏应力多元回归模型的试验研究

喻 秋, 李顺才,2, 陈 飞

(1. 江苏师范大学 机电工程学院, 江苏 徐州 221116；2. 江苏师范大学 江苏圣理工学院, 江苏 徐州 221116)

拉伸、扭转组合变形在工程中很常见,直升机上与螺旋桨相连的轴、钻探工程中在变形井眼中工作的钻杆都承受拉扭组合作用,学者研究了材料在拉扭组合作用下的力学行为[1-16]。

承受拉扭组合变形的构件,不同的拉伸、扭转加载速率以及不同加载顺序都对其破坏应力及破坏方向产生不同程度的影响,当然不可能一一试验得到破坏应力。目前,尚未有针对拉扭组合变形在不同加载条件下破坏应力的经验公式。因此,有必要通过试验来建立经验公式或预测模型,从而得到不同加载条件下的破坏应力及破坏面方向,为建立拉扭组合变形的强度条件及疲劳寿命提供理论及试验依据。

1 试验系统与试件

试验设备为力尔牌拉扭组合多功能试验机,型号为DLNKJ-150-500,如图1所示,该试验机的最大试验力为150 kN,最大扭距为500 N·m。扭转速度调节范围为0～5 r/min,扭转角度分辨值为0.018°。金属试验标准拉扭试件(见图2)的标距为100 mm、标准直径为10 mm。

图1 拉扭组合多功能试验机

图2 金属拉扭标准试件

2 试验方案

铸铁试件分别记为Z1、Z2、Z3和Z4,碳钢试件分别记为T1、T2、T3和T4,铝合金试件分别记为L1、L2、L3和L4。根据铸铁、碳钢和铝合金材料的性能差异制定的如载方案见表1。其中v,γ分别为拉伸、扭转加载速率。

表1 铸铁、碳钢和铝合金拉伸扭转的加载速率方案

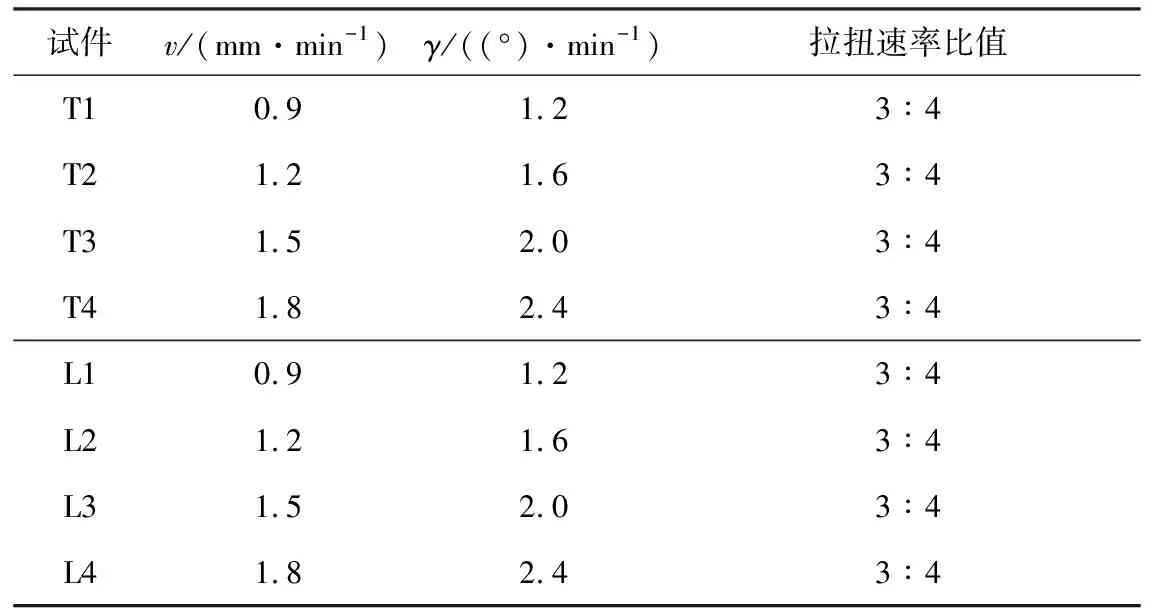
表1(续)

3 主要试验步骤

(1) 安装试件。将3种金属材料各取4根试件,在标距两端做好标记,将试件装入拉伸扭转专用夹头内,拧紧固定螺丝完成安装。

(2) 加载并采集信号。在软件操作界面,选定试验类型、完成参数设置后点击“启动”,进入校零阶段。之后按照表1试验方案设置拉伸和扭转加载速率加载,试验过程中同步采集拉力、扭矩、轴向变形及扭转角。

(3) 观察并量取试件破坏面的方向。试件断裂后将其从拉扭夹头中取出,观察其破坏面后拼接完整,测量并记录破坏面与横截面夹角,便于后续分析。

4 拉扭组合破坏应力及破坏方向的理论分析

如图3所示,试件在拉力F及力偶M作用下,产生拉扭组合变形。危险点在试件表面,构件表面A点的单元体应力如图4所示。

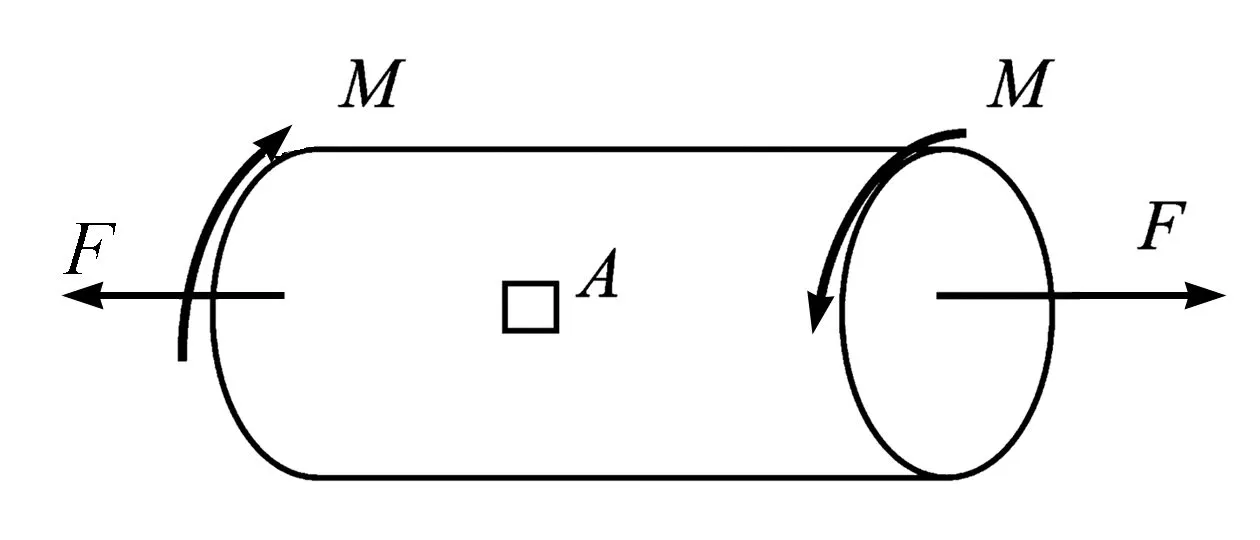
图3 杆件拉扭组合示意图

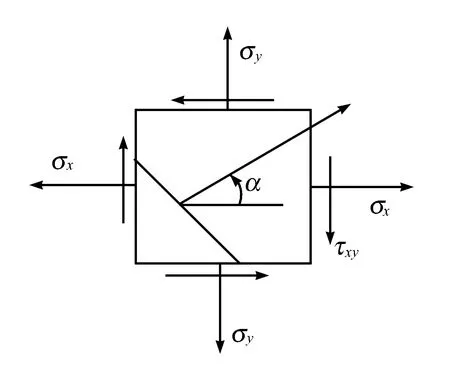
图4 单元体应力

不同金属材料的拉扭破坏一般表现为脆性断裂或塑性剪切破坏。基于平面应力状态理论得到经过A点的各斜截面上的最大正应力(主应力)σ1及最大剪应力τmax。

最大正应力的计算公式为

(1)

正应力方向与横截面夹角α0的计算公式为

(2)

最大剪应力的计算公式为

(3)

最大剪应力所在面与横截面的夹角α1满足:

(4)

5 试验结果及分析

5.1 不同加载速率下试件的载荷-变形曲线

铸铁、碳钢和铝合金3种材料的轴力-轴向位移曲线分别见图5(a)、(b)和(c),扭矩T-扭转角θ曲线分别见图6(a)、(b)和(c)。

图5 不同拉扭加载速率下试件的轴力-轴向变形曲线

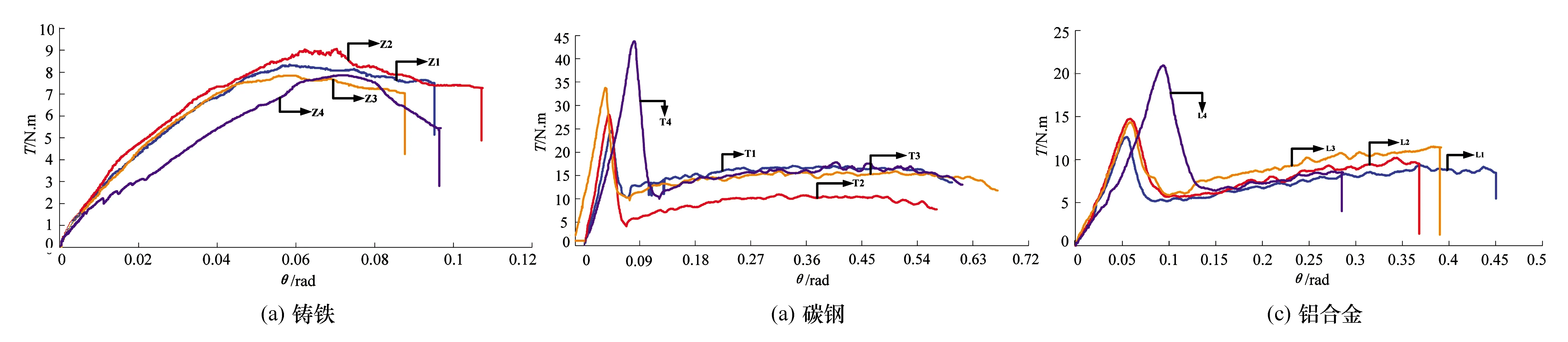
图6 不同拉扭加载速率下试件的扭矩-扭转角曲线

由图5及图6可知,铸铁的加载破坏呈现脆性断裂特征,而中碳钢和铝合金表现为塑性屈服特征,铝合金的弹性模量及强度极限比碳钢低。

分别记最大载荷为Fm、最大拉伸正应力为σm及延伸率为δ,记最大扭矩为Tm、最大扭转切应力为τm及扭转角为θ,得到3种试件的力学性能参数如表2所示。

表2 试件拉扭力学性能

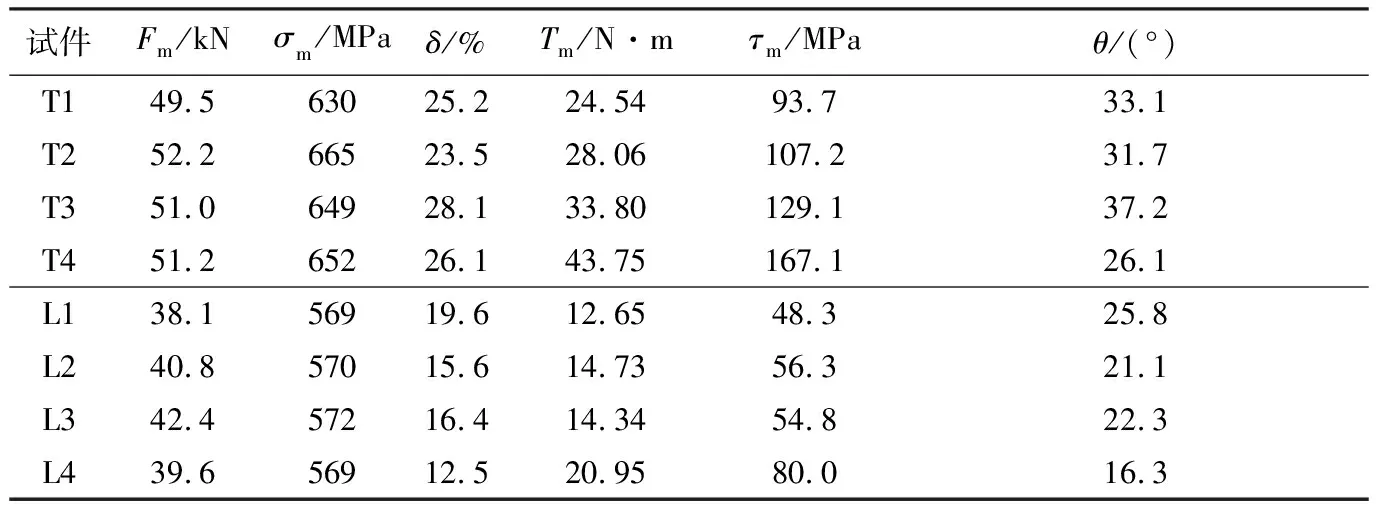
表2(续)

5.2 不同加载速率下试件的破坏应力和破坏面方向

根据表2中试验所得最大轴力及最大扭矩代入公式(1)、(2),得到铸铁的破坏应力σ1及破坏面方向α0如表3所示。代入公式(3)、(4),得到碳钢和铝合金的破坏应力τmax及破坏面方向α1如表4所示。

表3 铸铁破坏应力及破坏方向的试验计算值

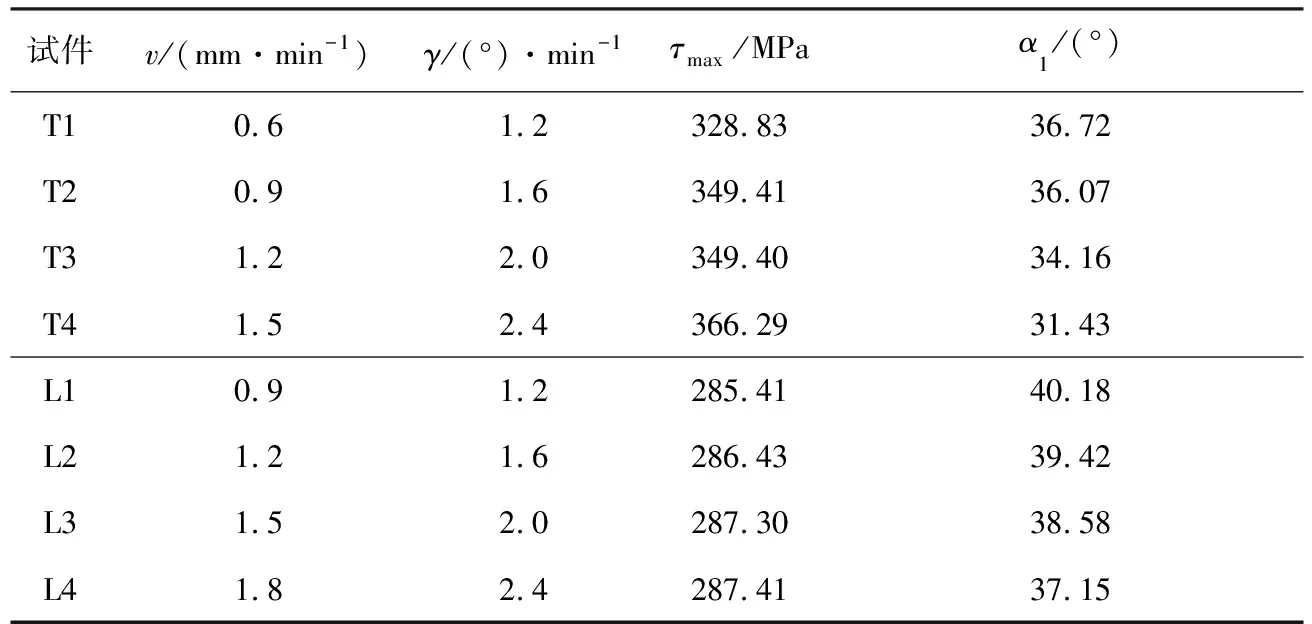
表4 碳钢、铝合金破坏应力试验值及破坏方向的计算值

根据表3和表4数据绘制3种试件的破坏应力和破坏面方向随加载速率的变化曲线,分别如图7和图8所示。

由图7可知,随着加载速率的增加,3种材料的破坏应力总的呈现增加趋势，铸铁主应力的增加幅度为6.67%，碳钢及铝合金破坏时剪应力的增加幅度分别为11.39%、0.70%。

由图8可知,3种材料破坏面与横截面的夹角随加载速率的变化规律不同。随加载速率的增加,铸铁破坏面与横截面夹角的绝对值增加了20.25%。而碳钢与铝合金破坏面与横截面夹角分别减少了14.41%和7.54%。

5.3 试件破坏面方向的实测值

拉扭破坏后的试件破坏面如图9所示。用游标卡尺量取斜面长度L斜面,见图10，计算破坏面与横截面的夹角α实测,实测结果见表5。

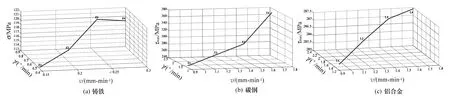
图7 3种材料的破坏应力随拉扭加载速率的变化曲线

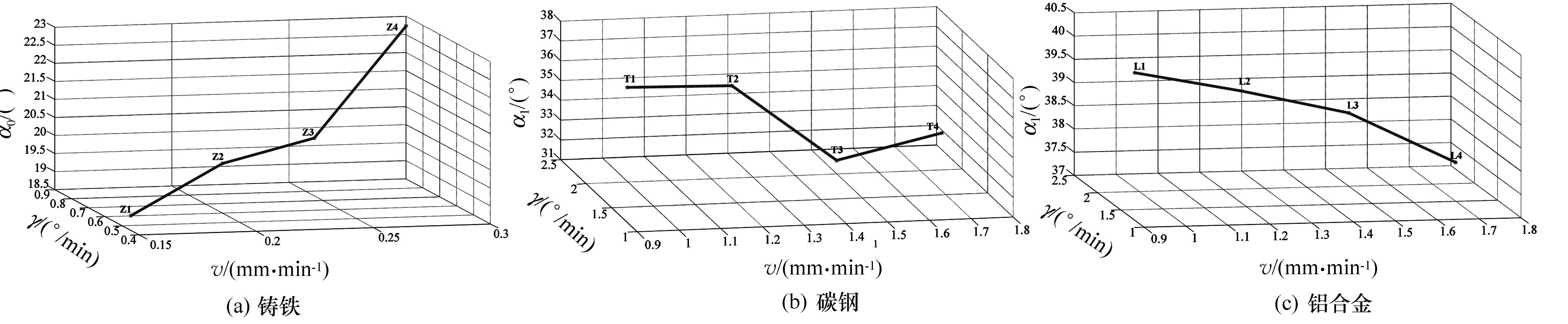
图8 3种材料破坏面方向随加载速率的变化曲线

图9 拉扭破坏试件的断面图

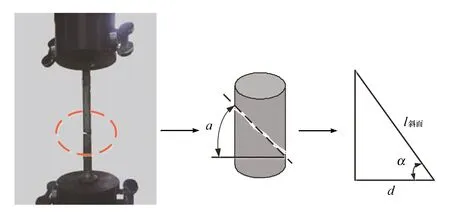
图10 计算试件破坏面方向示意图

试件v/(mm·min-1)γ/((°)·min-1)α0/(°)α实测/(°)α^/(°)Z10.150.45-18.91-19.37-18.64Z20.200.60-19.88-20.84-19.95Z30.250.75-20.10-20.84-21.03Z40.300.90-22.74-22.19-21.95T10.91.236.7233.5637.45T21.21.636.0732.8235.18T31.52.034.1630.4533.51T41.82.431.4331.2732.21L10.91.240.1842.2140.42L21.21.639.4239.7239.18L31.52.038.5838.6238.24L41.82.437.1537.4737.49

6 回归模型及其参数确定

结合试验数据,基于最小二乘法原理，分别建立材料破坏应力及破坏面方向关于拉伸、扭转加载速率的回归模型,利用Matlab软件编程求解模型中的未知参量。

6.1 破坏应力关于拉伸、扭转加载速率的拟合模型

设材料拉扭破坏应力关于拉伸加载速率、扭转加载速率的拟合式为

(5)

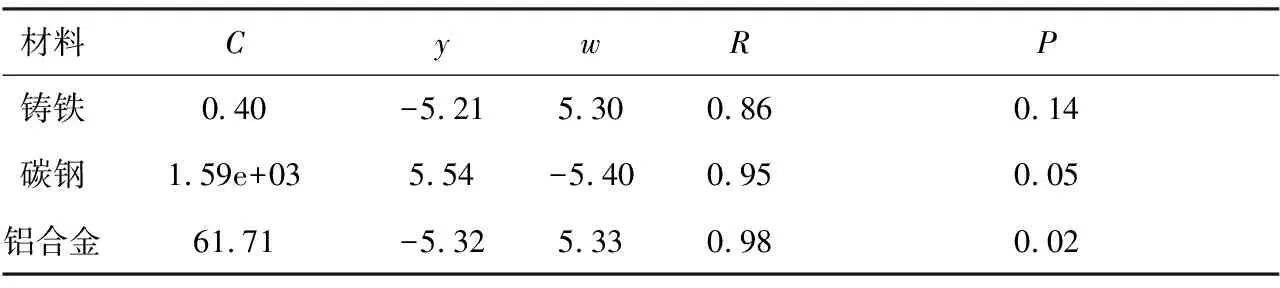
表6 金属材料破坏应力拟合相关性结果

图11 试件破坏应力的试验值、拟合值对比曲线

6.2 试件破坏面方向关于拉伸、扭转加载速率的拟合模型

同理,设破坏面与横截面夹角关于拉伸加载速率、扭转加载速率的关系式为

(6)

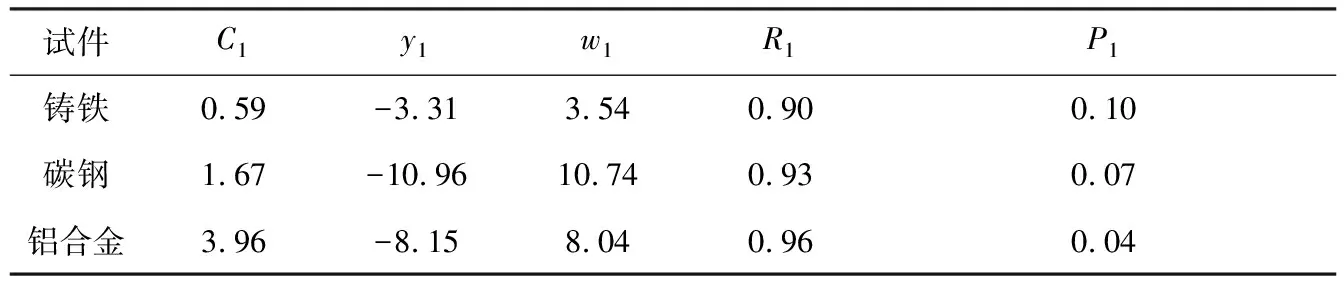
表7 材料破坏面方向拟合相关性结果

图12中破坏面方向的实测值与拟合值很接近,同时综合表6与表7可知,3种材料的拉扭破坏应力及破坏面方向拟合值与计算值的相关性系数R、R1值均高于0.85,表明依据建立的拟合模型可以较好地预测同一材料在给定拉扭加载速率下的破坏应力及破坏面方向。

图12 破坏面方向的试验计算值、实测值与拟合值对比曲线

7 结语

通过3种金属材料在不同加载速率的拉扭试验,得到了相应速率下的载荷-变形曲线。分别采用最大拉应力理论、最大剪应力理论建立了铸铁、碳钢和铝合金的拉扭破坏准则,基于试验数据计算了破坏应力及破坏面方向,并实测了破坏面与横截面夹角。基于最小二乘法原理分别建立了破坏应力、破坏面方向关于拉扭加载速率的拟合模型。研究表明，所得模型能较好地预测同种材料在不同加载速率下的破坏应力及破坏面方向。在条件许可下可以进行更多材料在4级以上加载速率下的拉扭试验,所得结论应更具有普适性。

[1] Nikitin A, Palin-Luc T, Shanyavskiy A. Fatigue crack initiation and growth on an extruded titanium alloy in gigacycle regime: comparison between tension and torsion loadings[J]. Procedia Structural Integrity, 2016, 2:1125-1132.

[2] Xue Z, Faleskog J, Hutchinson J W. Tension-torsion fracture experiments-Part II: Simulations with the extended Gurson model and a ductile fracture criterion based on plastic strain[J]. International Journal of Solids & Structures, 2013, 50(25/26):4258-4269.

[3] Faleskog J, Barsoum I. Tension-torsion fracture experiments—Part I: Experiments and a procedure to evaluate the equivalent plastic strain[J]. International Journal of Solids & Structures, 2013, 50(25/26):4241-4257.

[4] Sun L, Zhang M, Hu W, et al. Tension-Torsion High-Cycle Fatigue Life Prediction of 2A12-T4 Aluminium Alloy by Considering the Anisotropic Damage: Model, Parameter Identification, and Numerical Implementation[J]. Chinese Journal of Solid Mechanics, 2016, 29(4):391-406.

[5] Zheng X, Zhao K, Wang H, et al. Failure criterion with given survivability for ceramic notched elements under combined tension/torsion[J]. Materials Science & Engineering A, 2003, 357(1/2):196-202.

[6] Ayoub G, Naït-Abdelaziz M, Zaïri F, et al. Multiaxial fatigue life prediction of rubber-like materials using the continuum damage mechanics approach[J]. Procedia Engineering, 2010, 2(1):985-993.

[7] 郑修麟, 赵康, 王泓,等. 拉/扭复合应力下脆性材料断裂的一般准则[J]. 机械工程材料, 2004, 28(2):7-9.

[8] 胡桂娟, 张克实, 莫智莉. 45号钢后继屈服与塑性流动试验的Chaboche模型分析[J]. 广西大学学报(自然科学版), 2014, 39(1):171-179.

[9] 刘世民, 艾素华, 王中光. LY12铝合金的拉扭复合加载疲劳[J]. 航空材料学报, 2006, 26(5):96-100.

[10] 雒设计, 赵康, 王荣. S135钻杆钢的拉扭复合加载疲劳行为[J]. 材料工程, 2013(1):40-44.

[11] 贾晓亮, 王晶, 张亦良,等. 复杂应力状态下典型材料全载荷过程中的力学行为[J]. 应用基础与工程科学学报, 2017(2):407-418.

[12] 赵石雷. 拉扭等比例加载下典型材料全寿命过程中的力学行为[D]. 北京:北京工业大学, 2014.

[13] 刘波. 拉扭复合受力条件下金属材料的失效研究[D]. 天津:中国民航大学, 2016.

[14] 姚晓鹏. 拉扭循环加载下缺口件应力应变分析与寿命预测[D]. 兰州:兰州理工大学, 2010.

[15] 朱仲伟. 基于变温下钛与镍的拉伸扭转力学性能试验研究[D]. 长春:吉林大学, 2016.

[16] 刘汉武. 拉伸-扭转作用下杆的有限变形问题研究[D]. 哈尔滨:哈尔滨工程大学, 2011.