单桩静载荷试验数据的优化计算和可靠性分析

高 春 杰

(上海飞耀岩土工程有限公司,上海 200600)

0引言

在单桩静载荷试验中，由于设备的安装、堆载物的重量没有按照规范的要求做以及环境、人为的因素等等，导致检测数据偏离正确的测试值，表现在沉降曲线上，其检测数据偏离正常值。在对检测数据进行分析时，通常需要对这些偏离值进行修正，修正的方法常常因人而异，没有一个统一的标准，因此寻找一种在一定的理论指导下的科学的修改方法，是很有必要的。文献[1]通过拟合曲线的方法，提出了对单个偏离值进行修改方法，并用一个质量指标来衡量修改的质量。但是，实际的单桩静载荷试验中，试验数据的偏离值往往不止一个，本文提出了一种当偏离值数目大于1的时候数据的修改方法，同时本文也提出了判断是曲线可靠性的方法。

1 函数逼近法用于单桩静载荷试验数据的优化修改

对于摩擦端承桩来说，理论的Q—s曲线应该是一条光滑连续的曲线，但在实际的测试中，实测的Q—s曲线是由有限个数据确定的折线表示的。我们可以根据有限个实测数据，应用函数逼近理论，可近似的求出理论Q—s曲线，并且应用近似的Q—s曲线，求得对应于任意加载量时的位移值，这就是函数逼近法用于数据优化修改的理论基础。

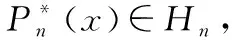
若沉降曲线的函数表达式为y=f(x)，有限个实测数据为(x1,y1),(x2,y2),…,(xn,yn)，取多项式:

(1)

则有方程组:

(2)

⋮

解此方程组可求得ai(i=1，2，…，n)，由此得到近似理论沉降曲线的函数为:

(3)

利用此函数可求得任意一点处的位移值。

(4)

(5)

摩擦端承桩的Q—s沉降曲线通常是一条逐渐下弯的曲线，曲线的形态可分为四个阶段：1)斜率基本保持不变的线性阶段(通常在前两级加载阶段，此时土体的变形处于弹性变性阶段)；2)部分桩侧土逐渐进入塑性变形阶段，Q—s沉降曲线的斜率逐渐增加，不再是一个常数，相对于第一阶段曲线下弯明显；3)随着桩身位移的进一步增加，桩端土反力迅速增加，使得Q—s将曲线的斜率的增加速率逐步趋缓；4)桩侧和桩端土的变形进入塑性阶段，桩端位移迅速增加，沉降曲线进入陡降阶段。

用函数逼近进行单桩静载荷试验数据优化修改时，首先要判断实测数据中的奇异值，其判断的方法主要基于理论Q—s曲线的形态特征。

例1：图1为单桩静载荷试验的Q—s曲线，灰色线为实测的Q—s曲线，黑色线为用函数逼近法修改后的Q—s曲线。

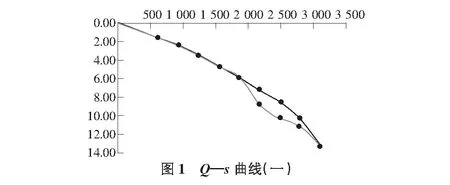
表1 位移值汇总表(一)

荷载修改后位移实测值00.0006201.541.549302.372.371 2403.433.431 5504.654.651 8605.915.762 1707.168.722 4808.4810.162 79010.2411.043 10013.1513.15

实测曲线的第六级、第七级的实测数据明显为异常值，考虑到奇异值的发生是一个逐渐的过程，因此把第五级和第八级的数据也列为需要修正的数据。由图1可见，修正的效果很好，修正前后的位移汇总表见表1。

位移逼近函数的多项式系数见表2。

表2 位移多项式系数(二)

由表1，可以算出实测的Q—s沉降曲线相对修正后的Q—s沉降曲线的最大绝对偏差和偏差度见表3。

表3 数据偏差表(一)

最大绝对偏差和偏差度越大说明实测的Q—s沉降曲线的可靠性越差。

2 曲线拟合法用于实测曲线可靠性分析

文献[1]给出了修改单个异常点的计算公式，拟合函数为：

s(x)=a0P0(x)+a1P1(x)+…+anPn(x)

(6)

P0(x)=1

P1(x)=(x-b1)P0(x)

(7)

Pk+1(x)=(x-bk+1)Pk(x)-ckPk-1(x)(k=1，…，n-1)

(8)

(9)

质量指标σL：曲线拟合的质量指标σL为:

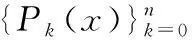
例2：图2为单桩静载荷试验的Q—s曲线，灰色线为实测的Q—s曲线，黑色线为最优拟合后的Q—s曲线，其数值见表4。

表4 位移值汇总表(二)

由表5可见其位移多项式系数只有两个，也即n=1；由表6可见曲线拟合的质量指标等于0.41，表明实测曲线与拟合曲线的吻合度较高。据此可以判断实测的Q—s沉降曲线近似于一条直线。

表5 位移多项式系数(二)

表6 数据偏差表(二)

据上分析可初步判断，实测的Q—s沉降曲线的可靠性差。

进一步分析实测数据，该单桩静载荷试验采用两台内径200 mm的200 t的千斤顶，实测平均油压和加载量见表7。

表7 实测油压和加载量表

可见实际的加载量小于设计的加载量。

3 结语

基于多项式逼近的沉降数据的修改方法，其修改后的逼近曲线与Q—s真曲线的偏差度，取决于实测数据中准确数据数目的多少及分布的均匀性，实际操作中，至少应保证准确的数据不少于全部沉降数据的1/2，并且保证修改前后的最终沉降量不变。满足此条件的逼近曲线，可以将其看作Q—s真曲线的近似曲线，再以此近似曲线作为计算实测曲线绝对偏差和偏差度的基准。应用多项式逼近对沉降数据进行修改时，应保证第一级荷载所对应的位移值为正常值。

最优拟合曲线法拟合后的Q—s曲线，可以分为直线和曲线两种。对于最优拟合曲线为直线情形，按照Q—s曲线特征判断，检测数据可判断为可靠性差。通常其主要原因是：1)设计的最大加载量远小于单桩的极限承载力；2)试桩的堆载量严重不足；3)试桩的参数设置不准确；4)设备安装不规范；5)人为的干预加载量等。

参考文献:

[1] 谢才军.单桩检测数据的优化计算和承载力预测[J].工业建筑,2012,42(sup):426-429.

[2] 叶其孝，沈永欢.实用数学手册[M].第2版.北京：科学出版社，2006:250,716.

[3] JGJ 106—2014,建筑基桩检测技术规范[S].