无需信源数目的改进TOFS算法*

曾耀平

（西安邮电大学通信与信息工程学院，西安710121）

1 引言

最初的高分辨角度估计都是基于窄带信号展开的，但实际中，雷达、声纳等系统收到的信息通常都是宽带信号。对于宽带系统而言，如果直接运用基于窄带的MUSIC算法，对于方位估计首先往往会得到错误的角度估计信息；其次，宽带信号相对于窄带信号而言，携带的信息更多，充分利用这些信息往往能得到更为精准的估计结果，因此宽带系统受到了更为广泛的关注。最早的宽带DOA估计算法是非相干信号子空间法[1](ISSM)，该方法原理简单、估计结果有效，但运算量较大，相干源下估计会失效。文献[2]提出的相干信号子空间法(CSSM)克服了ISSM的缺点，在相干源下有效，且在强噪声下也有良好的分辨能力。经典的CSSM法有旋转信号子空间法[3]（RSS:Rotational Signal Subspace），双边相关变换法[4]（TCT:Two-sided Correlation Transform）等。不过CSSM算法预先获知宽带信源的数目信息，这会带来额外的运算量且会带来累加误差。文献[5]提出的投影子空间正交性测试法（TOPS:Test of Orthogonality of Projected Subspaces），该算法无需事先估计信源的数目，但是需要选择一个频点作为估计的参照频点，不当的参考频点会带来附加的估计误差，同时也会带来虚假谱峰；另外TOPS算法在强噪声下也往往会失效。基于TOPS算法，文献[6-7]提出了TOFS（Test of Orthogonality of Frequency Subspaces）算法，该算法同样也不需要聚焦运算，且由于同时利用了多个频点的信号和噪声子空间的正交性，该算法的估计性能要优于TOPS算法，且避免了虚假谱峰现象。随着技术的发展，新的正交类宽带信号的方位估计技术层出不穷[8-9]，受到学者和科技工程人员的广泛关注。TOPS、TOFS算法有效的前提是必须获得信源的先验数目，在工程应用中，信源先验数目是需要预估的，由于背景噪声的干扰，预估经常会出现误差，如何在信源预估不当的条件下进行准确的角度测向是一个困扰工程科技人员的难题。为此，本研究提出一种无需信源数目的改进TOFS算法。

2 宽带阵列信号模型

TOFS算法利用的是每个频点的噪声子空间；为避免噪声子空间不准确给算法带来的影响，改进TOFS算法利用了协方差矩阵的全部奇异值向量，同时对所有的奇异值向量进行加权，这样就可避免信号特征向量对噪声子空间的影响，从而获得较为精确的噪声子空间。

为便于描述，我们用符号(·)T、(·)*、(·)H、E{·}来代表转置、共轭、共轭转置、均值。观测阵列是均匀线列阵，阵元个数为M，P个宽带信号从远场入射到阵列上，其入射角度分别为 θ1，θ2，...，θp，以阵列的第一个阵元作为参考阵元，阵列的输出为

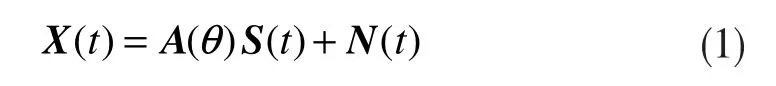
其中，X(t)为 M×1 维阵列输出矢量，A(θ)是 M×P 维方向矩阵，S(t)是P×1维信号矢量，N(t)是M×1的噪声矢量，其中X(t)=[x1(t),x2(t),...,xM(t)]T，S(t)=[s1(t),s2(t),...,sP(t)]T，N(t)=[n1(t),n2(t),...,nM(t)]T。

宽带信号最常用的DOA估计方法一般都是在窄带信号前提下进行的，如果将现有的DOA估计方法不经处理直接套用在宽带信号中，由于带宽的拓展将会导致阵列信号子空间的维数也会相应被扩展，进而会因此导致其谱峰的位置与信号的真实方位角度出现较大偏差，造成DOA估计失效。在宽带DOA估计里，方向矢量中的相移由两方面的因素决定，即方位角和频率，所以即使来波信号的空间角度一样，频率不一样，也会引起其相移不同。所以在宽带信号下，当进行谱峰遍历搜索时，方向矢量不能采用一个固定频率，否则会造成DOA估计失效。所以对于宽带信号，不能直接利用经典的窄带信号时域模型。

此时需要对接收数据进行离散傅里叶变换，得到阵列输出的频域宽带信号模型

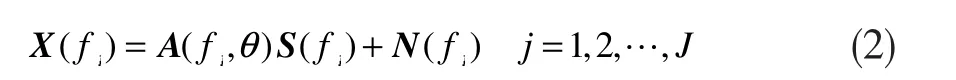
其中

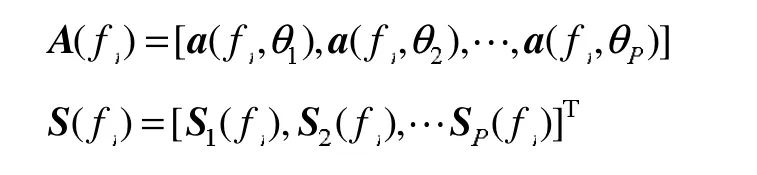
对fj的数据矢量X(fj)进行协方差运算，得到频点fj的协方差矩阵RX(fj)

将式（8）计算得到的卫星本振频率结果代入到式（14）即可得到频率的稳定度。计算分析显示，在取样时间1 s和10 s时，稳定度约为 4.8×10-11和1.7×10-11，在取样时间100 s和1 000 s时，稳定度约为 1×10-10和 1×10-9。分析结果表明，卫星本振短期稳定度比较好，长期稳定度会逐渐变差。

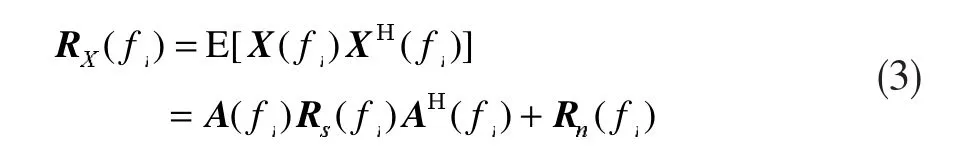
对RX(fj)进行特征分解，按照特征的大小可以得到对应的特征向量，进而可得到对应频点的噪声子空间和信号子空间，再利用聚焦类CSSM算法就可以获得宽带信号的角度估计值。

3 TOPS及TOFS算法

TOPS是一种宽带非相干方法。该方法是利用噪声子空间和信号子空间的正交性来进行方位估计，当信号频率和入射角度满足

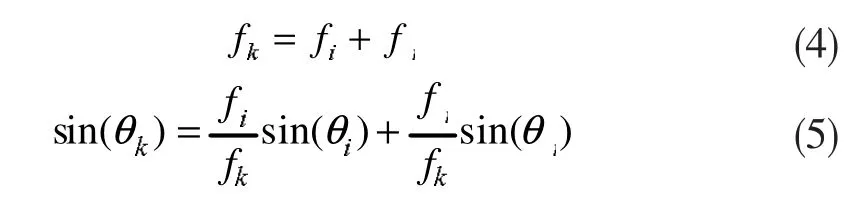
对于某个给定的导向向量，必定存在着某个矩阵Φ(fj，θj)且同时满足下列条件

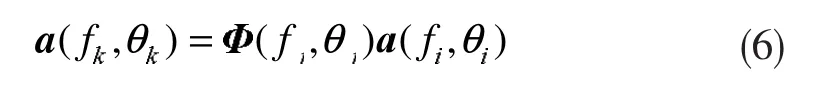
其中，Φ(fj，θj)=diag{a(fj，θj)}为转换矩阵，利用Φ(fj，θj)可以把某一频率和某一角度处的导向向量转换为另一频率和另一角度处的导向向量。

当 θi= θj时，则 θk= θi，且满足

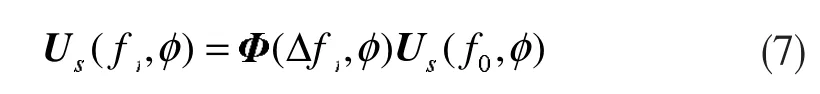
式(7)表明，通过矩阵转换，在保证信号角度不变的情形下，可将阵列导向向量从带宽范围内的某个频点变换到另外一个频点。

定义一个M×P维的矩阵Δfi=fi-f0，F0是给定参考频点的信号子空间。利用构造如下的矩阵

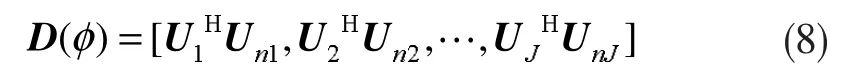
其中，Ui，Uni是 fi频点所对应的信号及噪声子空间。当φ恰好为阵列流形的某个角度时，D(φ)会出现缺秩现象，利用D(φ)的缺秩，通过一维角度遍历扫描即可得到宽带源的DOA估计值。

TOPS算法性能优劣与所选的参考频点关系密切，频点选择不当会使算法出现虚假的谱峰。TOFS算法利用全部子带的噪声子空间和信号子空间均满足正交这一特性，即当φφ为信号的空间方位时，存在

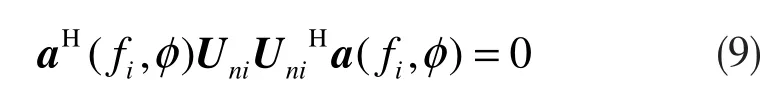
利用J个标量J,可以构造一新矩阵

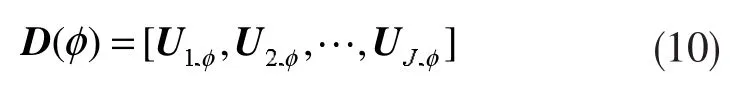
通过判断向量D(φ)中各元素接近零的程度，就可获得宽带信号的DOA估计。TOFS算法综合了多个子带信息，其估计性能要高于TOPS算法，且不会出现虚假谱峰。

4 改进的TOFS算法（MTOFS）

公式(10)里的Uni指的是fi频点对应的噪声特征向量矩阵，一般来说要获得Uni需对RX(fj)进行特征分解，根据小特征值来获得Uni，前提条件是需要知道信源的先验数目。由于强噪声的干扰，在工程上精确获得准确的估计数是非常困难的。进一步分析得知，当信源数目未知时，对RX(fj)进行特征分解后，可利用所有的特征向量，同时对所有的特征向量进行加权，这样,不同的特征向量对谱的作用就会不同。选择适当的加权系数，可消减信号特征向量对角度谱的影响，这就是MTOFS算法的基本思想。对RX(fj)进行特征分解获得所有的特征向量矩阵并对所有的特征向量矩阵进行加权，构成的新矩阵

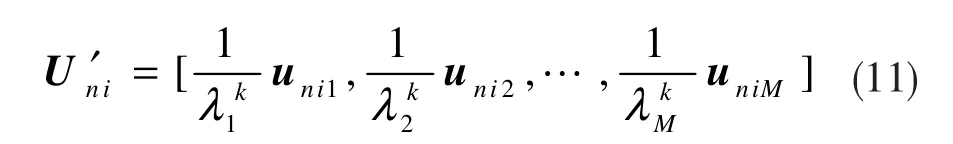
利用J个标量J，可以构造一新矩阵

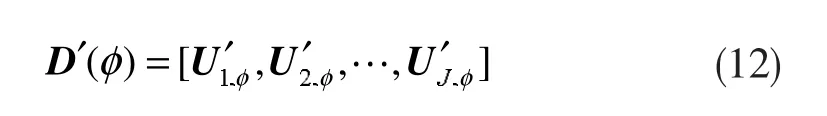
通过判断向量D'(φ)中各元素接近零的程度，就可获得宽带信号的DOA估计。MTOFS算法无需信源的先验信息且综合了多个子带信息，无论信源是欠估计还是过估计，甚至无需对信源估计就可以实现宽带信号的DOA估计。

5 仿真结果及分析

仿真采用的阵列是均匀线列阵，阵元个数为6，有2个远场宽带信号入射到阵列上；入射角度分别是 10°、20°，信号的带宽相同，同为 30Hz；中心频率均为90Hz。入射噪声是零均值的平稳高斯白噪声，且和入射的宽带信号相互独立。将宽带信号分为11个窄子带,每个子带的数据采样数均为256。

为了比较研究，在同样的仿真条件下对TOPS、TOFS、MTOFS算法分别进行仿真，结果如图1、图2所示。

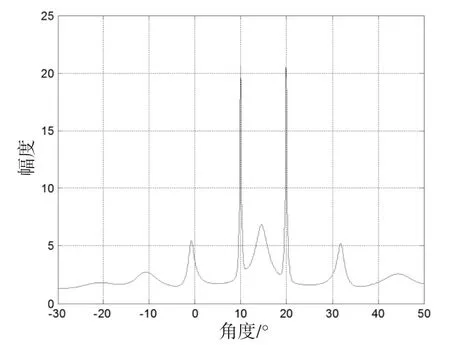
图1 TOPS算法的角度谱

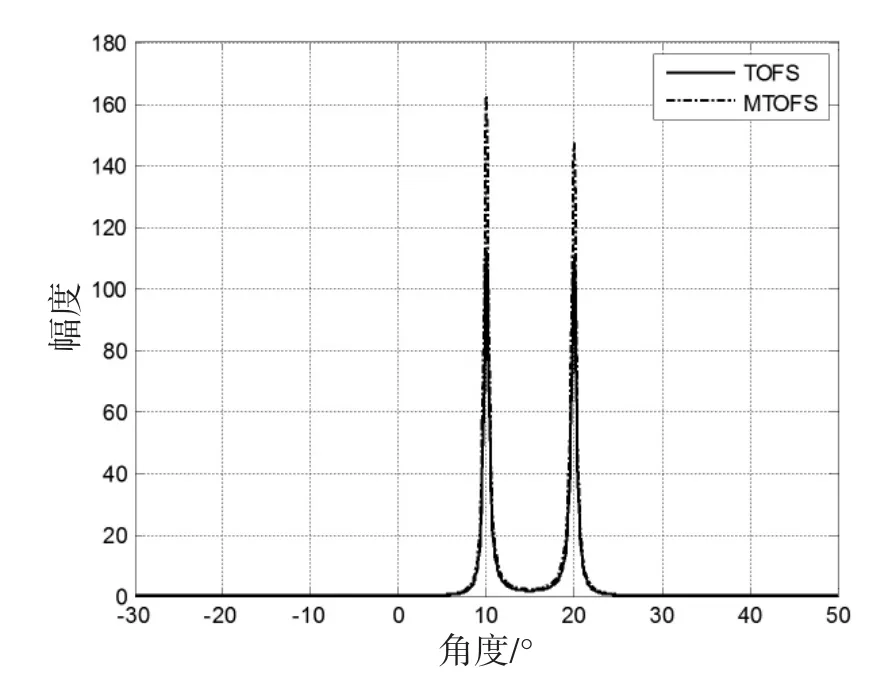
图2 TOFS及MTOFS算法的角度谱

图中仿真结果表明，TOPS算法由于与选择的参考频率有关，当参考频率选择不当时，算法就会出现伪峰；而TOFS算法由于利用了多个频点的信息，可以消除伪峰。MTOFS算法在选择合适的加权系数后，无需信源的先验信息，也能准确地估计出信号的方位角。算法的均方根误差曲线如图3所示，从中可见，TOFS与MTOFS的均方根误差区别不大，估计性能相当。

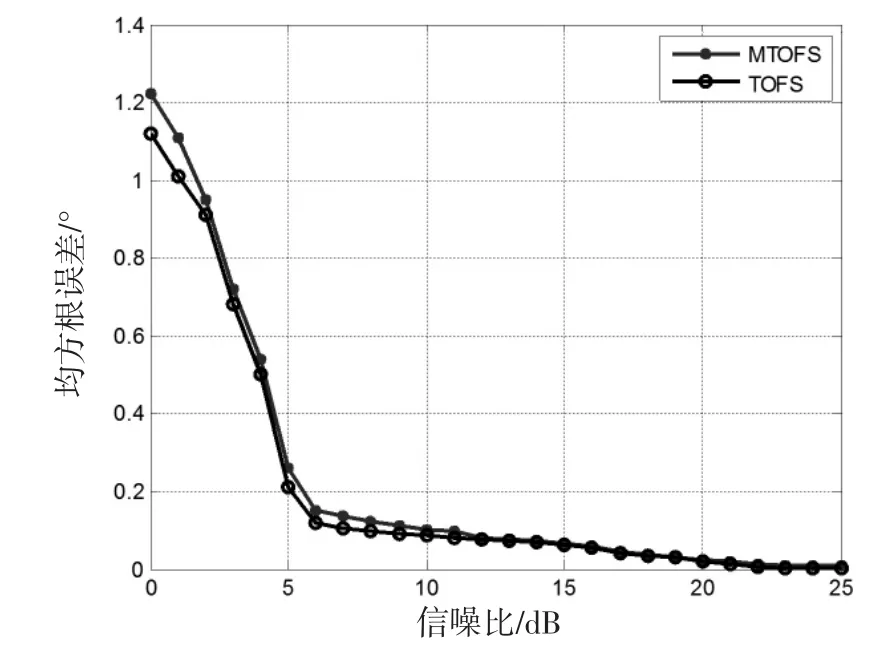
图3 TOFS及MTOFS算法的均方根误差曲线

6 结束语

本研究出了一种适合于宽带信号的无需预知信源数目的DOA估计新算法。该方法对带宽范围内所有频点的特征向量进行全空间加权，结合TOFS算法，解决了TOPS算法容易出现伪峰的难题，无需信源预估就可以实现宽带信号的高分辨角度估计。仿真结果验证了算法的有效性。

[1]WAX M,SHAN T J,KAILATH T.Spatio-temporal spectral analysis by eigenstructure methods[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1984,32(4):817-827.

[2]WANG H,KAVEH M.Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1985,33(4):823-831.

[3]HUNG H,KAVEH M.Focussing matrices for coherent signal-subspace processing[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,2002,36(8):1272-1281.

[4]VALAEE S,KABAL P.Wideband array processing using a two-sided correlation transformation[J].IEEE Transactions on Signal Processing,2002,43(1):160-172.

[5]YOON Y S,KAPLAN L M,MCCLELLAN J H.TOPS:new DOA estimator for wideband signals[J].IEEE Transactions on Signal Processing,2006,54(6):1977-1989.

[6]YU H Q,HUANG Z T,LIU J,et al.TOFS:A new DOA estimator for wideband sources[J].Journal of Astronautics,2007,28(5):1304-1313.

[7]于红旗,徐欣,黄知涛,等.一种新的宽带DOA估计方法[J].信号处理,2009,25(1):118-121.YU Hongqi,XU Xin,HUANG Zhitao,et al.A new wideband DOA estimation method[J].Signal Processing,2009,25(1):118-121.

[8]蔡进,刘春生,陈明建,等.聚焦的子空间正交性测试宽带DOA估计方法[J].信号处理,2018,34(2),221-228.CAI Jin,LIU Chunsheng,CHEN Mingjian,et al.A test method for wideband DOA estimation with focused subspace orthogonality[J].Signal Processing,2018,34(2),221-228.

[9]侯文林,郭英,张坤峰,等.宽带共形阵列信源方位与极化联合估计算法[J].上海交通大学学报,2016,50(5):764-770.HOU Wenlin,GUO Ying,ZHANG Kunfeng,et al.Joint estimation algorithm for azimuth and polarization of wideband conformal array source[J].Journal of Shanghai Jiaotong University,2016,50(5):764-770.