检测单相电压暂降的直接导数算法

蒋海玮，李东辉

（大连交通大学电气信息工程学院，大连116028）

1 引言

根据电气与电子工程师协会(IEEE)标准IEEE Std.1159-1995的定义，电压暂降是指供电电压方均根值下降至额定值90%～10%的事件，其典型持续时间为工频0.5～30周波[1-2]。在各种常见的暂态电能质量问题中，电压暂降的发生频率最高,其对可调速驱动装置、自动化生产线、可编程逻辑控制器、交流接触器以及计算机系统等敏感设备均可产生巨大危害，严重影响了人们的生产与生活[3-5]。为了实现电压暂降的实时补偿以及为暂降事后的统计与分析工作提供依据，必须解决额定电压暂降特征值实时检测的问题。

针对暂降特征值的实时检测，坐标变换法以其良好的动态性能和较高的检测精度受到许多学者的广泛关注。传统的坐标变换法将单相电压延时60°构造虚拟三相系统，再将abc坐标下的电压变换至dq坐标，最后用低通滤波法提取dq分量中的直流成分从而计算暂降幅值及相位跳变[2，6]。在此基础上，一些学者考虑到构造三相系统的过程运算量大，将单相电压求导或延时90°构造两相静止坐标下的电压，用αβ-dq变换代替了abc-dq变换以获取dq分量[7-9]。然而，坐标变换法必然涉及额外电压相量的构造，所需参量较多。另外，各文献对伴有长时间频率偏移情况下的相位跳变检测的研究较少，导致坐标变换法只能检测±90°范围内的相位跳变。

鉴于上述电压暂降检测方法存在的不足，设计了一种检测电压暂降的直接导数算法，并将其应用于实测电压暂降的检测。结果表明，该算法运算量小，可以满足检测装置对实时性和准确性的要求，同时扩展了频率偏移情况下较长时间电压暂降相位跳变的检测范围。

2 αβ变换法检测电压暂降特征值

αβ变换法是基于坐标变换的电压暂降特征值检测的典型方法。设暂降过程中的理想单相电压为u(t)，先将u(t)投影至αβ两静止坐标系下，可得到投影值为：

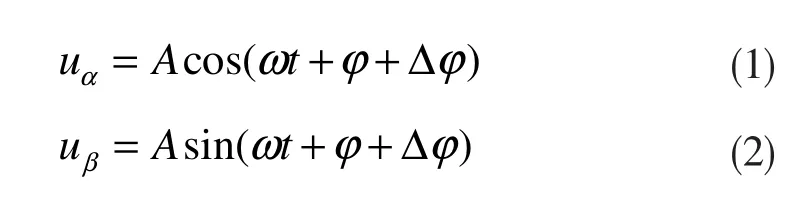
两式中，uβ可视为当前电压的瞬时值。对于uα的构造有两种方法：一种是延时1/4周期的构造法，即将所测得的电压延时1/4周期以获得uα；另一种方法如式(3)所示，即通过求导的方法来构造uα。

再对uα和uβ进行两相静止两相旋转变换，可得到dq轴下的电压ud和uq，具体变换过程如下：

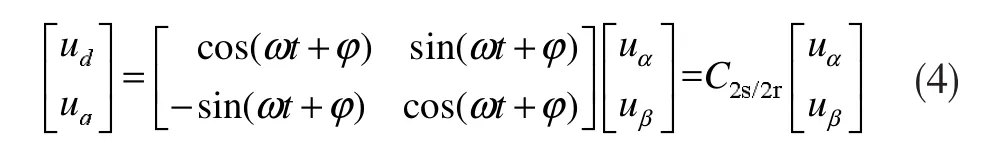
变换矩阵C2s/2r的构造需要与暂降前电网电压同相位的正弦信号sin(ωt+φ)和与之对应的余弦信号cos(ωt+φ)，它们需由锁相环和一个正、余弦信号发生电路产生。

接着通过低通滤波器得到dq轴电压的直流分量Ud0和Uq0，最终可求得暂降的基波电压幅值和相位跳变为：

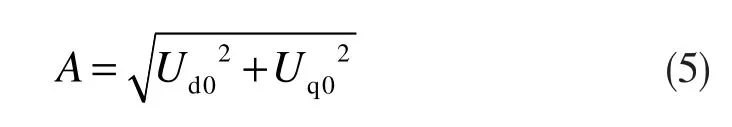
3 直接导数算法检测电压暂降特征值

考虑到坐标变换法所需的额外电压信号较多，且检测超过±90°的相位跳变时会出现问题，为此设计了用于单相电压暂降检测的直接导数算法。

首先建立暂降前和暂降过程中理想相电压函数模型，如式(7)和(8)所示：

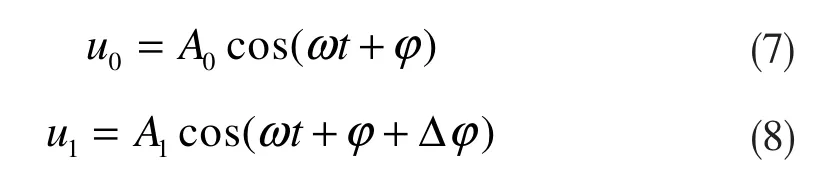
式中，A0为系统额定相电压幅值（为已知量），A1为暂降过程中相电压幅值，φ为电压初相角，Δφ为相位跳变。

3.1 电压暂降幅值计算

对(8)式求导可得：

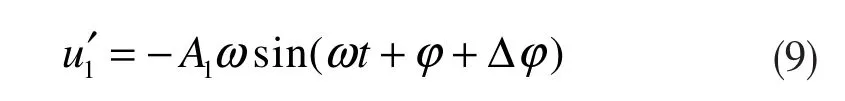
理想情况下，由式(8)、(9)便很容易得出暂降基波电压幅值为：

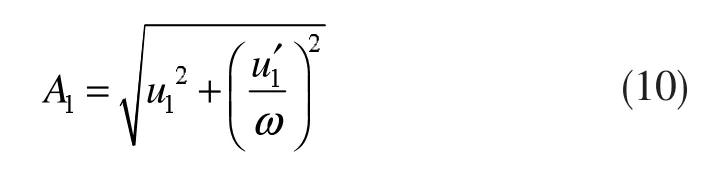
假定电压暂降幅值为k,根据定义可得最终的暂降幅值表达式：

在实际应用中,的计算只需要u1中相邻的两个采样数据，即u1对应tk时为utk，则对应tk-1时为ut(k-1)，此时任意时刻电压的导数为：

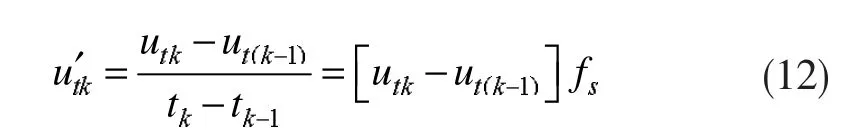
式中fs为采样频率，常用的采样频率为6.4kHz、12.8kHz和25.6kHz等，远大于工频50Hz的两倍，故计算的导数值精度很高。另外，我国规定380V低压配电系统电压总谐波畸变率不应超过5%，随着电压等级的升高，各级高压配电系统电压总谐波畸变率还会逐渐降低[2]。因此，由于电网谐波电压幅值数量级相对基波较小，当式(8)中含有谐波电压时，谐波对基波暂降幅值的检测结果所带来的影响可以忽略，通过低通滤波提取式(11)中的直流分量即为暂降幅值。

3.2 电压暂降相位跳变计算

如式(6)所示，针对相位跳变的检测，人们往往习惯于通过坐标变换等数学手段构造出仅以相位跳变 Δφ 为变量的三角函数值 sin(Δφ)或 tan(Δφ)，再对其做反三角函数运算，从而求得相位跳变值[6-11]。然而由于反正弦函数和反正切函数只能计算出±90°范围内的相位跳变值，故无法检测在较长时间电压暂降过程中因系统频率偏移而导致的绝对值超过90°的瞬时相位跳变[7]。为此，本文将相位跳变的检测范围扩展至±180°（相位跳变绝对值超过90°的情形参见下文4.2中的讨论），并提出基于暂降过程中电压 u1的实时相位(ωt+φ+Δφ)与暂降前电压 u0延续波的实时相位(ωt+φ)作差来求取相位跳变Δφ的方法。其中，暂降前电压延续波可由相应处理器的内存对暂降前电压一周期的瞬时数据周期延拓来生成，也可由锁相环产生（暂降前电压与暂降前电压延续波在后文中统称为暂降前电压）。

假定 θ0=(ωt+φ)、θ1=(ωt+φ+Δφ)。将 u0和 u1及其导数化为幅值为1的形式，从而确定电压实时相位的正、余弦值：

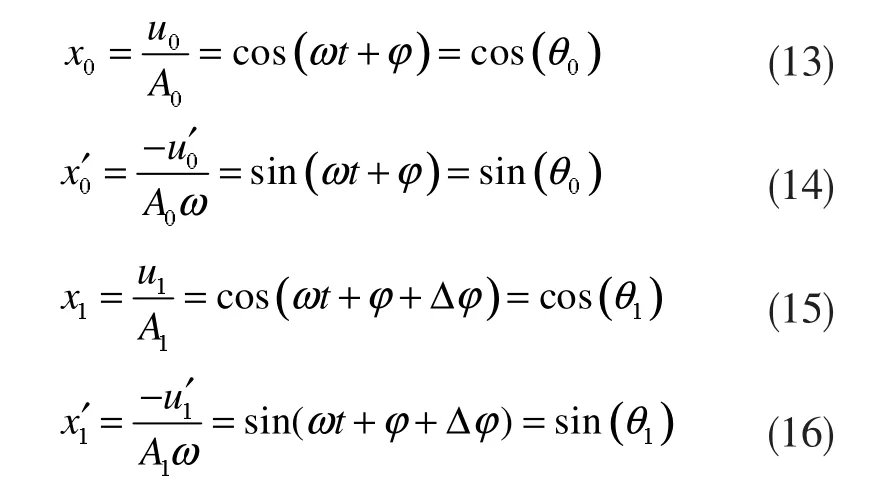
已知相位角的正、余弦值，即可确定该相位角所在的象限，从而可将相位表示为随时间的推移在-180°～+180°范围内周期变化的函数，以 θ1为例：

同理，将上式中的角标1替为0，即可获得θ0的表达式。至此，u0和u1的实时相位便确定了。为了获得相位跳变Δφ，将式(7)和式(9)中的x0和x1视为两个同频率的简谐运动方程，其所对应的单位旋转矢量如图1所示，旋转矢量在x轴正方向的投影即为x0和的瞬时值。其中，暂降电压视为由暂降前电压转过小于180°的那个角度而产生，这个角度值即为相位跳变的绝对值若暂降电压由逆时针旋转产生（如图1中则 Δφ 为正值；若由顺时针旋转产生（如图1中，则 Δφ为负值。

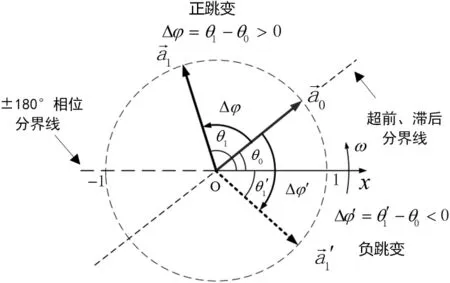
图1 电压暂降旋转矢量模型

⑴ 若旋转至的过程中未穿越±180°相位分界线，此时存在-180°≤θ1-θ0≤180°，则相位跳变Δφ= θ1-θ0（如图 1所示）。

⑵ 若旋转至的过程中逆时针穿越±180°相位分界线，此时存在θ1-θ0＜-180°，相位跳变Δφ=（如图 2所示）。

⑶若旋转至的过程中顺时针穿越±180°相位分界线，此时存在 θ1-θ0＞180°，相位跳变Δφ=（图2中与的位置互换时）。

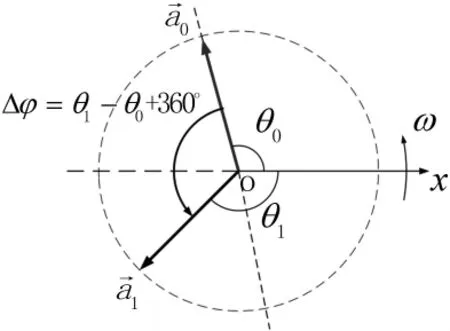
图2 0逆时针穿越±180°相位分界线

综上可将相位跳变表示为：

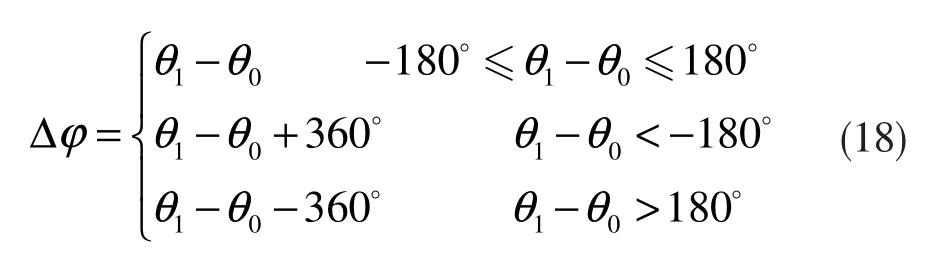
当电压中含有谐波时，对于式(17)而言，由于反三角函数的级数展开式中不包含平方项，故谐波不会对相位跳变的检测带来额外的直流分量，通过低通滤波提取Δφ中的直流分量即为相位跳变值。

4 理想暂降波形仿真验证

利用MATLAB仿真工具，编写M脚本文件生成10kV配电网在额定状态下发生单相电压暂降的波形。暂降幅值k=0.5，持续时间为6个周波（0.12s），相位跳变 Δφ=30°,暂降的发生与终止都是瞬时的。由此得到电压暂降瞬时波形如图3所示。

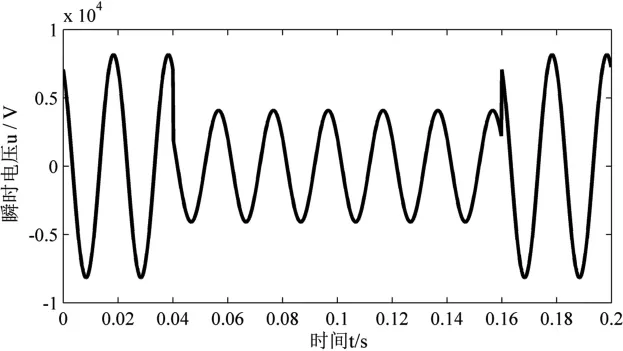
图3 电压暂降瞬时波形图

从图3可以看出，电压在0.04s发生了暂降，0.16s时暂降终止。设定采样频率为6.4kHz（0s处的数据为第一个采样数据，每周期采样128个数据，下文的检测也均采用这一采样频率），采用3种方法分别检测10个周期的电压瞬时波形，所得的检测结果如图4～图6所示。

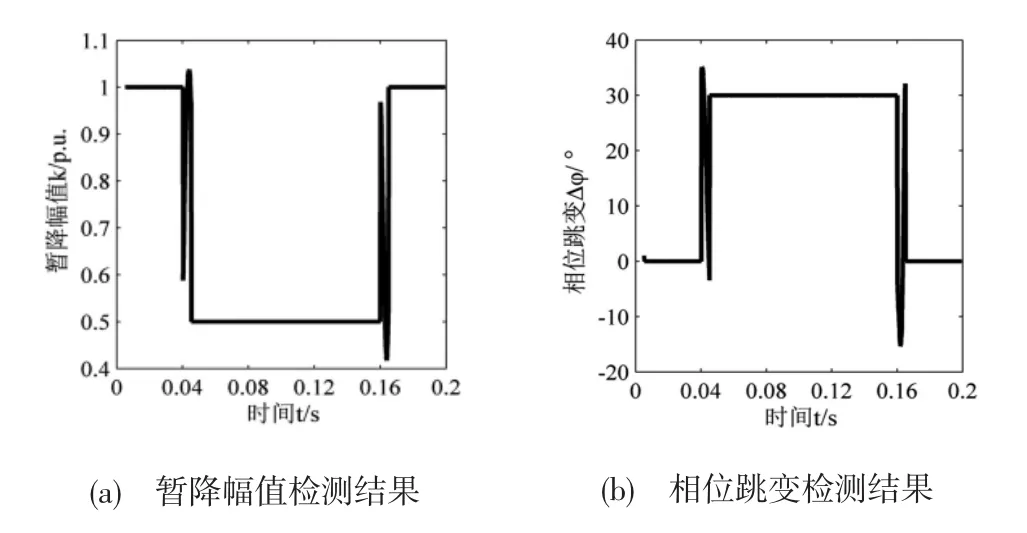
图4 延时90°的dq变换法

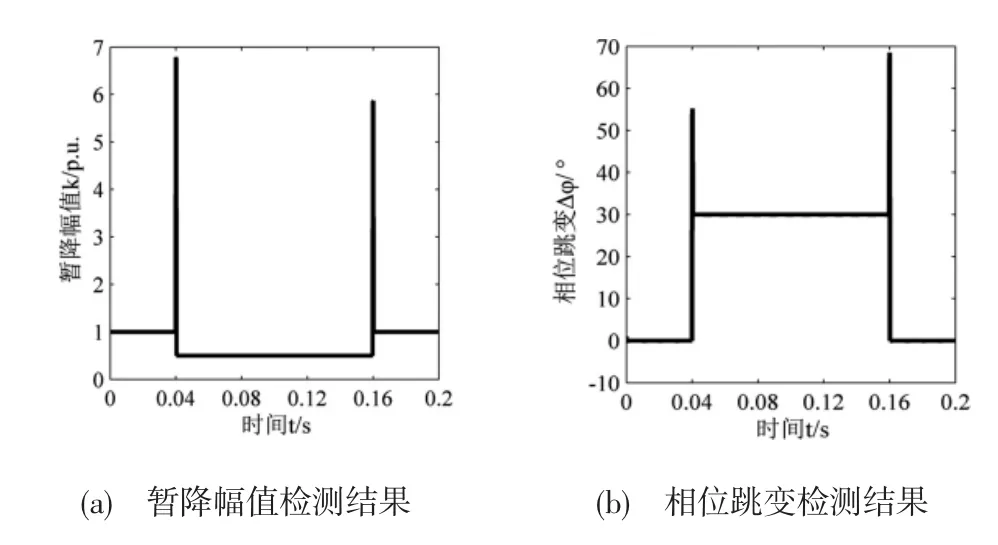
图5 求导的dq变换法

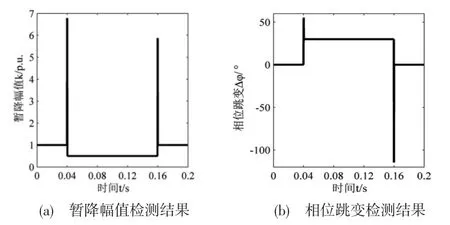
图6 直接导数算法

结果表明，三种方法均可获得精确的暂降特征值。但从检测的实时性上来看，延时90°的dq变换法存在着1/4周期的延时，而对于求导的dq变换法和直接导数算法而言，两者的检测仅延时了一个采样周期。其中，直接导数算法无需坐标变换，尤其对于暂降幅值的检测，运算量远小于求导的dq变换法，暂不考虑因波形不连续而造成的暂降起始与终止时刻的过冲现象，直接导数算法检测电压暂降的整体效果最佳。

5 实测暂降波形算法应用

5.1 伴有谐波的电压暂降检测

以某地区10kV配电网于2014年9月5日发生的一次伴有谐波干扰的单相电压暂降为例，采用本文的直接导数算法并复合低通滤波对该次电压暂降进行检测。仿真中LPF选择3阶、截止频率为100Hz的Butterworth滤波器。

如图7(a)所示，该系统的某一相在0.12s～0.38s之间发生了具有约25°相位跳变、48%的暂降，且由于暂降过程中伴有幅值不等的各次谐波和间谐波，暂降波形发生了一定程度的畸变。从图7(b)～(e)的检测结果可以看出，低通滤波可以较好的屏蔽谐波对暂降检测的干扰，滤波后的检测结果依然满足精度要求。由于Butterworth滤波器在准确性和快速性之间存在一定矛盾，在二、三次谐波电压的含有率很高时，可以采用小波分析对原始信号进行预处理[7]，再利用形态滤波法或级联型滤波器与本文的直接导数算法复合[12-13],从而提高检测的实时性。

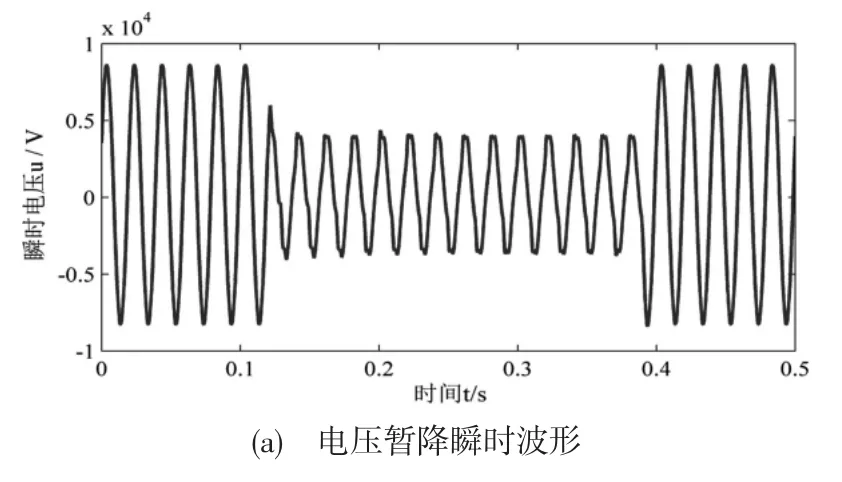
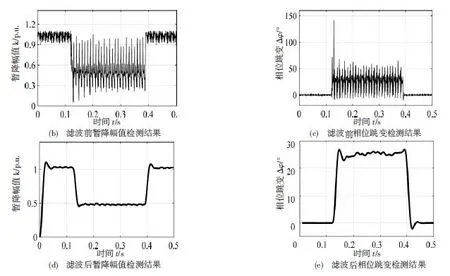
图7 畸变的电压暂降实测波形及检测结果

5.2 伴有频率偏移的电压暂降检测

目前对于相位跳变产生原因的解释主要基于电压暂降分压模型，由于故障发生前后系统的网络结构发生改变，母线电压相量的幅角也会随之改变，此时的相位跳变Δφ可视为两阻抗角的差值[2，14]，因此 Δφ 的范围介于-90°～+90°之间。然而，相位跳变的范围并不一定仅局限在±90°内[15]，如当相位跳变初始值接近-90°且有大容量（有功）负荷突增时，系统有功功率的不平衡所引起的频率负偏移会使相位跳变值变得更小。

实测数据表明，负荷突增后，在系统的频率进入振荡状态之前，通常存在一个线性的衰减区间[16]，而在机组旋转备用容量较小时，该区间长度往往会超过电压暂降的常见持续时间。设系统频率平均变化率为kf，伴有频率偏移的暂降电压函数可表示为：

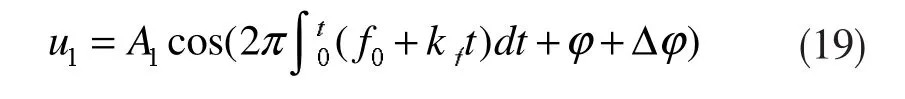
由此可得因频率偏移而引起的相位偏移量为：

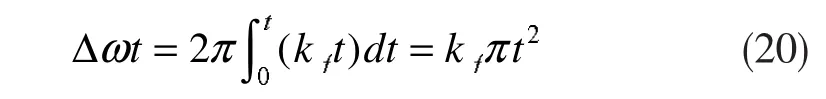
采用MATLAB编写程序，生成10kV配电网在额定状态下发生伴有频率偏移的单相电压暂降波。程序设定暂降起始时刻为0.25s，持续时间为1s，kf=-0.1Hz/s，φ=0°，Δφ=-80°。由式(19)可知，相位跳变值在0.25s时刻应由0°突变至-80°。由式 (20)可知，从0.25s开始，相位跳变应以二次函数形式单调减小，至1.25s暂降终止时，受频率偏移而引起的相位偏移量 Δωt为-18°，即相位跳变应为-98°。

采用三种方法对相位跳变进行检测，检测结果如图8所示。结果表明，正如第2.2节所述，反正切函数只能计算±90°范围内的相位跳变，故两种dq变换法在相位跳变递减至-90°时（约1s处）突变至了+90°，之后的检测结果也一直比真实值大180°，可见后期的检测结果是错误的。而直接导数算法已在原理上将相位跳变的检测范围扩展至了±180°，可以真实地反映相位跳变的递减过程。另外，从程序返回的检测结果来看，直接导数算法在暂降结束时检测到的相位跳变值为-98.0225°，可见其检测精度很高。因此，直接导数算法在检测伴有频率偏移的电压暂降时，效果优于其他三种方法。

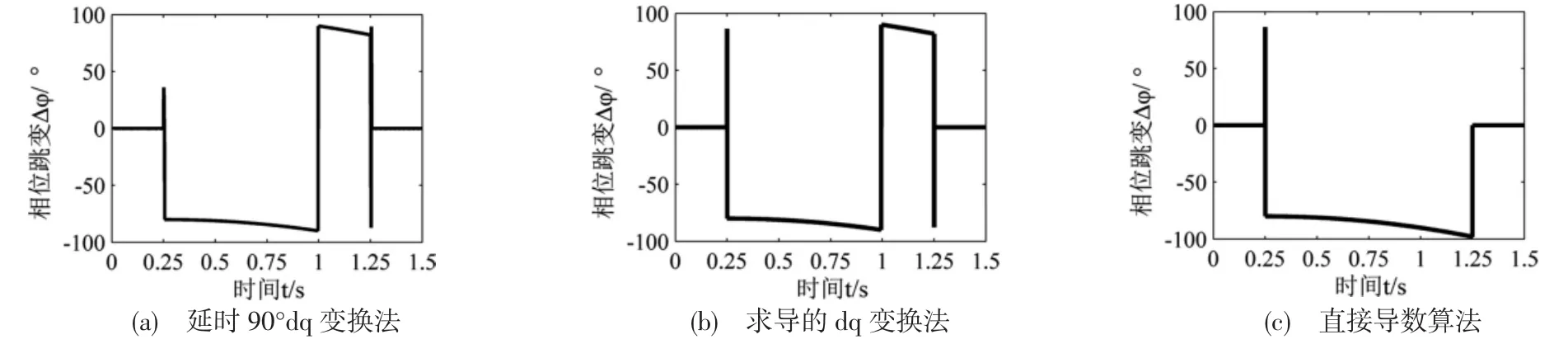
图8 伴有频率偏移的电压暂降相位跳变检测结果比较

6 结束语

基于正弦量与其微分量的关系及旋转矢量分析法，设计了检测单相电压暂降特征值的直接导数算法。将该法与现有dq变换法对比，表明直接导数算法在原理上无需坐标变换，减少了检测装置额外电压信号的输入数目。在实用中还可发现，当谐波总畸变率低于国家标准规定的限值时，复合低通滤波直接导数算法的检测结果仍可满足精度要求，此时检测的延时主要由数字滤波器本身特性造成。另外，对于相位跳变的检测，由于此法在原理上可以检测一周期范围内的相位跳变，因此该算法比坐标变换法更适用于伴有频率偏移的电压暂降的检测。

[1]BOLLEN M.Understanding power quality problems:voltage sags&interruptions[M].Hoboken,N.J.:Wiley-IEEE Press,1999.

[2]肖湘宁,韩民晓,徐永海,等.电能质量分析与控制[M].北京:中国电力出版社,2010.XIAO Xiangning,HAN Minxiao,XU Yonghai,et al.Analysis and control of electrical energy quality[M].Beijing:China ElectricPowerPress,2010.

[3]PETRONIJEVIM ,VESELIB ,MITROVIN,et al.Comparative study of unsymmetrical voltage sag effects on adjustable speed induction motor drives[J].Iet Electric Power Applications,2011,5(5):432-442.

[4]吴亚盆,刘颖英,徐永海.可编程序控制器对电压暂降敏感度的试验研究[J].电工技术学报,2018,33(6):1422-1430.WU Yapen,LIU Yingying,XU Yonghai.Experimental study on sensitivity of programmable controller to voltage sag[J].Transactions of China Electrotechnical Society,2018,33(6):1422-1430.

[5]徐永海,兰巧倩,洪旺松.交流接触器对电压暂降敏感度的试验研究[J].电工技术学报,2015,30(21):136-146.XU Yonghai,LAN Qiaoqian,Hong Wangsong.Experimental study on the sensitivity of AC contactors to voltage sag[J].Transactions of China Electrotechnical Society,2015,30(21):136-146.

[6]肖湘宁,徐永海,刘昊.电压凹陷特征量检测算法研究[J].电力自动化设备,2002,22(1):19-22.XIAO Xiangning,XU Yonghai,LIU Hao.Research on detection algorithm of voltage sag characteristic quantity[J].Electric Power Automation Equipment,2002,22(1):19-22.

[7]吴红春.基于小波及DQ算法的电压暂降检测方法研究[D].重庆:重庆大学,2008.WU Hongchun.Research on voltage sag detection method based on wavelet and DQ algorithm[D].Chongqing:Chongqing University,2008.

[8]蒋素琼.一种用于检测电压暂降的新方法[J].电气技术,2016,17(11):56-61.JIANG Suqiong.A new method for detecting voltage sag[J].Electrical Engineering,2016,17(11):56-61.

[9]汪加宏,侯新国,王黎明,等.基于求导和数字形态变换的电压暂降检测算法[J].电器与能效管理技术,2015(13):54-58.WANG Jiahong,HOU Xinguo,WANG Liming,et al.Voltage sag detection algorithm based on derivation and digital morphological transformation[J].Electrical appliances and energy efficiency management technology,2015(13):54-58.

[10]李希年,王彦文.单相电路电压暂降的求导检测算法[J].工矿自动化,2014,40(5):43-46.LI Xinian,WANG Yanwen.Derivative detection algorithm for voltage sag of single-phase circuit[J].Industry and Mine Automation,2014,40(5):43-46.

[11]马啸,应展烽,张旭东,等.电网单相电压暂降特征量检测的二点算法[J].科学技术与工程,2015(22):33-37.MA Xiao,Ying Zhanfeng,ZHANG Xudong,et al.Twopoint algorithm for detection of single-phase voltage sag characteristics in power grid[J].Science Technology and Engineering,2015(22):33-37.

[12]刘云潺,黄纯,欧立权,等.基于dq变换的三相不平衡电压暂降检测方法[J].电力系统及其自动化学报,2007,19(3):72-76.LIU Yunchan,HUANG Chun,OU Liquan,et al.Detection method of three-phase unbalanced voltage sag based on dq transform[J].Proceedings of the Chinese Society of Universities for Electric Power System and Automation,2007,19(3):72-76.

[13]周柯,罗安,夏向阳,等.一种改进的ip-iq谐波检测方法及数字低通滤波器的优化设计[J].中国电机工程学报,2007,27(34):96-101.ZHOU Ke,LUO An,XIA Xiangyang,et al.An improved ipiq harmonic detection method and optimization design of digital low-pass filter[J].Proceedings of the CSEE,2007,27(34):96-101.

[14]KAMBLE S,THORAT C.Characteristics analysis of voltage sagindistributionsystemusingRMSvoltagemethod[J].InternationalJournalonElectrical&PowerEngineering,2013.

[15]DJOKICSZ,MILANOVICJ V.Advancedvoltage sag characterisation.PartI:Phaseshift[J].IEEProceedings-Generation,Transmission and Distribution,2006,153(4):423-430.

[16]候智圆.电力系统频率动态行为特征分析[D].济南:山东大学,2012.HOU Zhiyuan.Analysis of frequency dynamic behavior characteristics of power system[D].Ji'nan:Shandong University,2012.