改进的SVR在大坝边坡位移预测中的应用

刘小生，于 良(江西理工大学，江西 赣州 341000)

修建电站、水库会形成大量人工开挖边坡。由于大坝边坡受水文气候、地质构造等重要因素的影响，导致边坡滑坡事件屡见不鲜，给人民的生产和生活带来了巨大影响并会造成财产损失，因此对边坡的变形预测和预警就显得尤为迫切和重要。在已经提出的许多预测方法中[1]，回归分析法实际工作时很难建立顾及各因素的非线性数学监控模型[2]；时间序列分析法很难针对特定数据构造合适的模型[3]；灰色理论对原始数据要求较高，当原始数据序列波动较大、信息过于分散时预测精度往往降低[4]；神经网络模型存在收敛速度慢和陷入局部极值等问题[5]。海量数据大量涌现，高维数据给传统机器学习方法提出了严峻的挑战。

支持向量机(support vector machine,SVM)较好地解决了以往困扰很多学习方法的小样本、非线性、过学习、高维数、局部极小点等实际问题，具有很强的泛化能力[6]。为了使支持向量机更好地运用到边坡位移预测中，近年来不少学者对支持向量机中参数寻优方法进行了改进研究。关于支持向量机参数寻优的方法，国际上并没有公认统一的最好方法。常用的方法有：网格法、粒子群算法、遗传算法。其中粒子群算法和遗传算法由于初始值随机选取，造成参数搜索结果随机性较大，需多次训练才能得到较好的参数[7]；传统网格法相对于粒子群算法和遗传算法参数寻优稳定，但搜索速度较慢，精度较低[8]。因此本文改进传统网格法的参数寻找范围和搜索步距，目的是为了防止参数选取范围过大而造成收敛速度过慢，步距不够小而造成找不到准确的参数组，从而得到改进网格法，并在此基础上进行改进的支持向量机大坝边坡预测研究。

1 改进的SVR大坝边坡位移预测模型构建

1.1 支持向量回归机

支持向量机是由Vapnik基于统计学习理论提出的一种机器学习方法[9]。目前分为支持向量分类机和支持向量回归机。支持向量回归机(support vector regression machine，SVR)基本原理[10]为：设原来的训练集为给定某边坡的监测数据

T={(xi,yi),i=1,2，…,l}∈(Rn×R)l

式中，xi∈Rn；yi=R,i=1,2，…,l。选取适当的精度ε>0和惩罚参数c>0，便可得到与线性分化相对应的原始问题

(1)

代入拉格朗日函数，求解凸二次规划问题，可解得

(2)

(3)

则得构造决策函数

(4)

运用“相似程度”的原理选取核函数，目前常用的核函数有线性核函数、多项式核函数、径向基核函数(RBF)。本文运用径向基核函数，构造函数变为

(5)

在支持向量机回归估计算法中，RBF核函数的参数g及惩罚系数c均为很重要的参数，其中，核函数g的选取决定了输入空间到特征空间映射的方式，惩罚系数c用于平衡训练误差和模型复杂度。因此必须找到较好的参数寻优方法，本文采用改进网格法对支持向量机进行参数寻优。

1.2 改进的网格法

针对径向基核函数的支持向量机而言，网格法参数寻优所要搜索的参数组为惩罚因子c和核参数g，将两个参数各自设置较大的搜索范围和较小的步距，形成一个二维空间的网格，遍历网格中所有交叉点，并用K折交叉验证方法得到每组的性能，最终取使系统达到最优的参数作为最佳参数。

当步距足够小，支持向量机惩罚因子c与径向基核参数g取值范围足够广，一定能够得到最优解，但同样也会花费很长时间。传统网格法参数寻优遍历网格中所有交叉点，往往只进行两步，粗搜过后只进行一次细寻,但是步距有可能没达到最小步距,参数范围也有可能不足够小，最终可能与最优参数错过。

针对传统的网格法参数寻优的不足，对传统网格法作出改进[11-12]，得到本文改进的网格参数寻优方法。先粗略搜索即大步距、大范围，即以2的幂次方沿着两个参数的不同增长方向生成网格，这样既能遍历所有参数，又能方便网格的收缩与增长。网格中的节点即为给定范围内所有可能得到的参数对；根据样本集，利用5-折交叉验证[13]找出最佳参数组，判断是否满足精度要求或结果稳定。如果满足要求，储存参数，参数优化结束；如果不满足要求，再把c和g的取值范围缩小到最优值左右并适当减小步距，如果同时出现两处最优位置，取c值较小的最优位置，依次类推，逐步减小步距与参数取值范围，直到满足精度要求或结果稳定为止。

1.3 SVR组合模型构建

为了消除或减弱基于启发式参数寻优算法的支持向量机边坡预测模型的不足，改进传统网格法参数寻优算法搜索速度较慢、精度较低等问题，提出了改进SVR组合预测模型。其具体思路如下：

首先，对原始数据做数据预处理。原始数据难免存在奇异值，运用“3δ准测”剔除奇异值，将剔除的奇异值“断链”现象运用内在物理联系、线性内插法、多项式曲线拟合等进行插补，由于所研究的数据可能不在同一个量纲单位，或为加快预测组合模型运行速度，因此需要对样本数据进行标准化处理，将样本数据归一化到区间[0，1]中。

其次，建立支持向量回归机。支持向量回归机寻求的是利用一个线性回归方程(函数y=g(x)可能为一维、二维、…、n维)去拟合所有的样本点，即使用y=g(x)来推断任意输入x所对应的输出值。求解回归方程可以将其简化为一个求二次凸规划问题，运用最小贯序列方法(sequential minimal optimization，SMO)等求解，依据“相似程度”的概念来选取适当的核函数，本文采用径向基核函数。

最后，运用改进的网格法进行支持向量机参数寻优。先粗略搜索即大步距、大范围，得到最优解大致位置，再把c和g的取值范围缩小到最优值左右并适当减小步距，如果同时出现两处最优位置，取c值较小的最优位置，依次类推，逐步减小步距与参数取值范围，直到满足精度要求或结果稳定为止。

图1为改进的SVR大坝边坡位移预测模型构建流程。

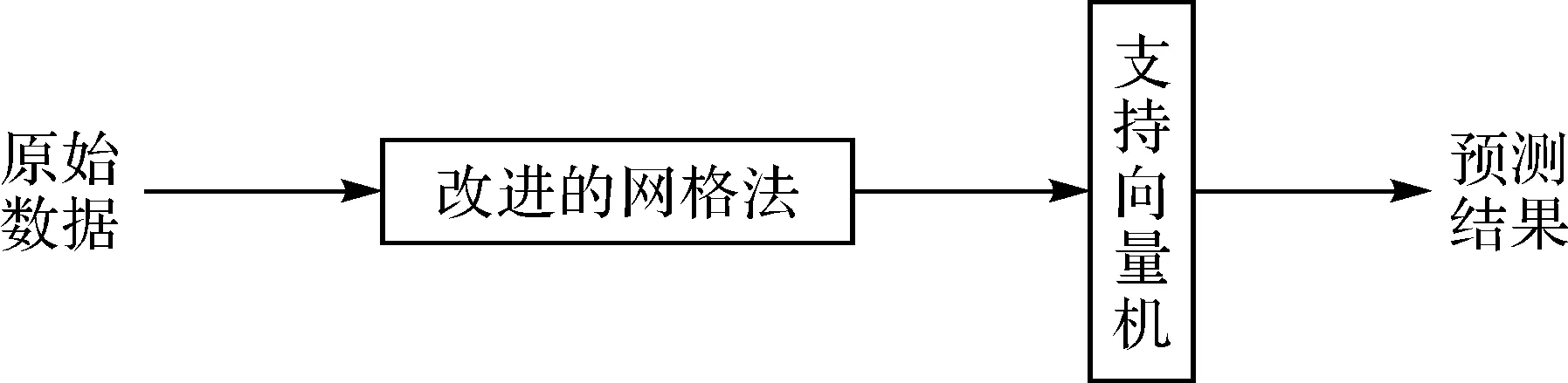
图1 改进SVR组合模型构建流程

2 工程应用

2.1 样本选择

试验采用的数据是锦屏一级工程坝区左岸缆机平台边坡位于f42-9断层出露部分的多点位移计M4-7(高程1886 m)的孔口位移数据，作为本文工程实例的原始数据[14],见表1。

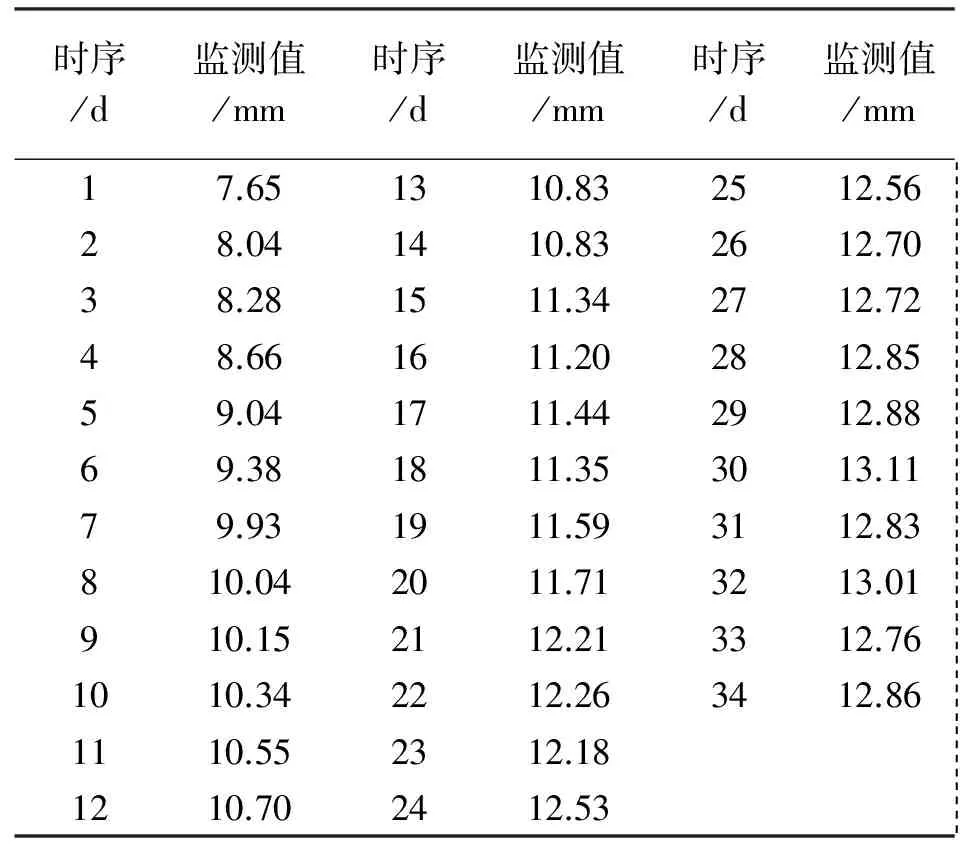
表1 M4-7观测点监测数据

2.2 预测步骤

采用基于改进网格法参数寻优的支持向量机的左岸缆机平台边坡的预测变形过程如下：

(1) 首先对左岸缆机平台边坡监测位移数据“剔异补缺”，然后将数据归一化到[0，1]。将观测数据1～30设为训练集，31～34设为测试集。

(2) 选择适当的核函数，由左岸缆机平台边坡监测位移数据可知，采用径向基核函数(RBF)为最佳选择。

(3) 用改进网格法搜索参数c、g，粗搜c的初始范围设为[2-8,28],g的初始范围设置为[2-8,28]。由于传统的网格法初始步距为1，因此本文改进网格法初始步距也设置为1。

(4) 采用K折交叉验证方法对训练集进行测试，其中K=5,初步得到最优参数c=0.4和g=11.6。

(5) 根据得到的最优值可将范围缩小c∈(2-4,24),g∈(2-4,24)，步距改为0.1，从而得到最优参数c=0.51、g=12.17。

(6) 继续步骤(5)细搜，范围缩小c∈(21.5,22.5),g∈(23,24)，步距改为0.01，依此类推，缩小范围和步距，最终得到最优参数c=0.574 3、g=12.125 7，使预测结果趋于稳定。

(7) 用得到的c=0.574 3、g=12.125 7在训练样本上进行训练，得出边坡预测模型。

(8) 用基于改进的SVR大坝边坡位移预测模型对样本数据进行测试。

2.3 测试结果及分析

试验平台采用Faruto等基于Matlab数学软件开发设计的加强版LIBSVM3.1-[FarutoULtimate3.1 Mcode]工具箱进行测试。用均方误差MSE作为评价指标

(6)

式中，Xi(i=1,2，…,n)为真实值；Yi(i=1,2，…,n)为预测值。MSE越接近于0，预测效果越好。SVR参数精确搜索3D效果图和等高线图，如图2、图3所示。

图2 SVR参数寻优(3D视图)

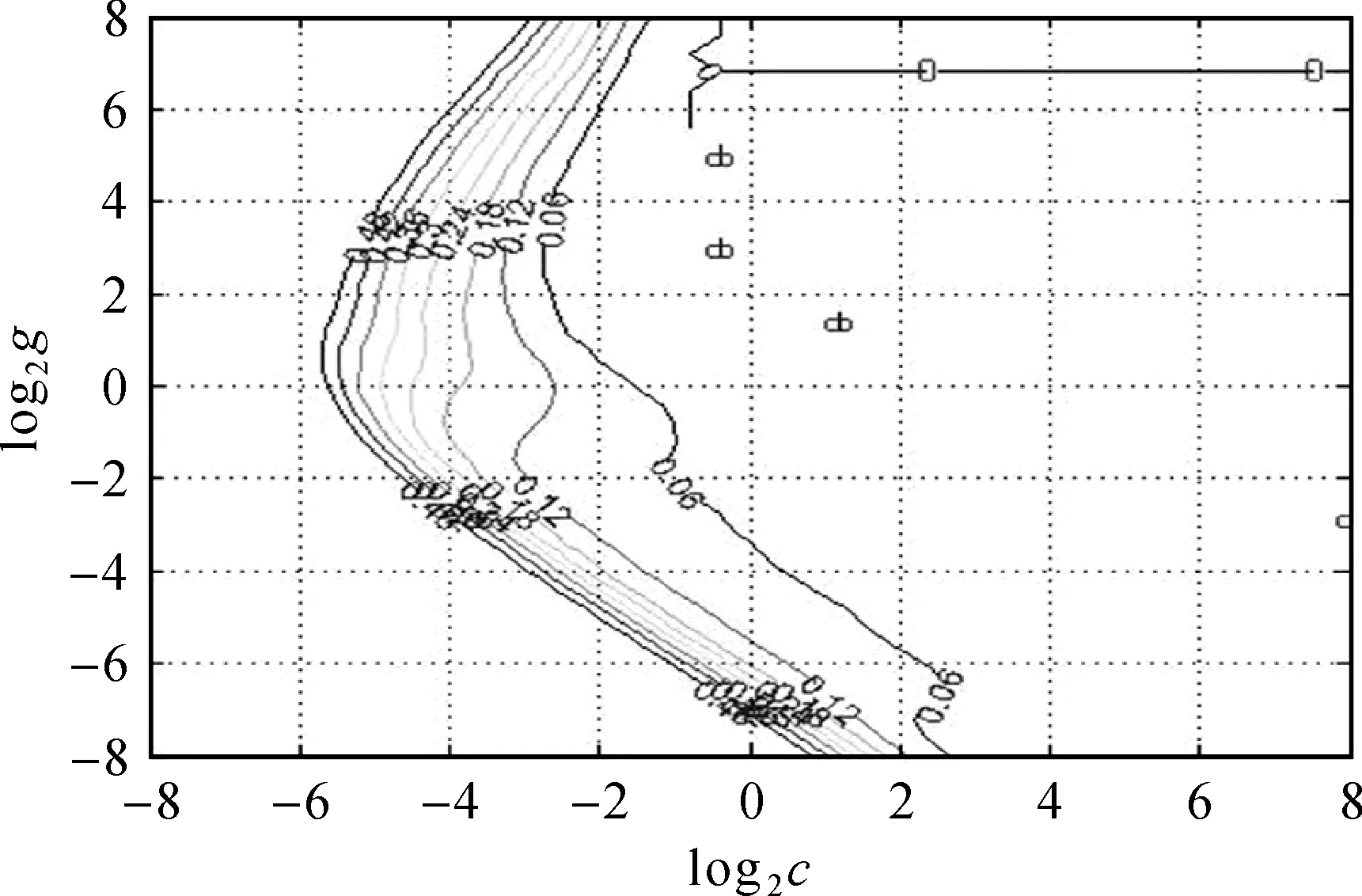
图3 SVR参数寻优等高线

为方便分析改进网格法参数寻优的支持向量机边坡预测模型所得结果的优越性，同时采用传统网格法的支持向量机预测模型进行了预测，预测误差用相对误差Erep表示，对比结果见表2。

(7)

式中，Xi(i=1,2，…,n)为真实值；Yi(i=1,2，…,n)为预测值。

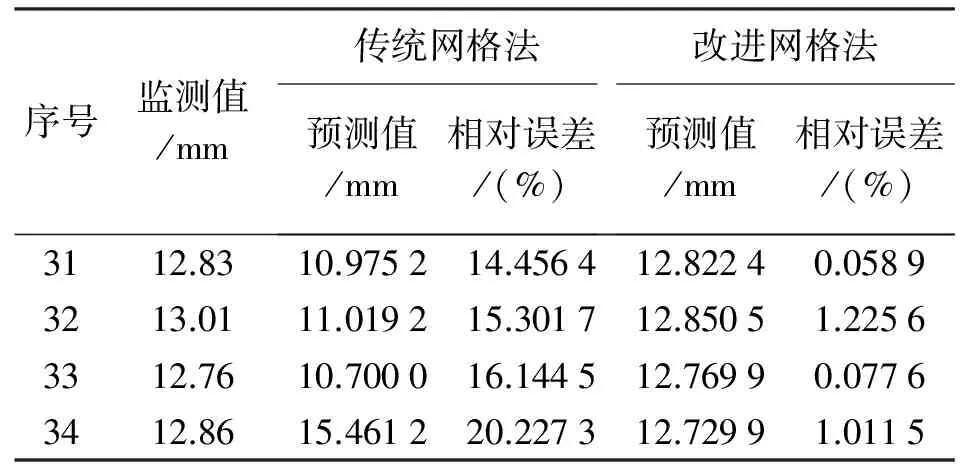
表2 M4-7监测点边坡变形预测结果

从表2可知，改进网格法参数寻优的支持向量机预测模型的相对误差最大为1.225 6%，最小为0.058 9%。传统网格法参数寻优的支持向量机预测模型的相对误差最大为20.227 3%，最小为14.456 4%。两种最大相对误差相差19.001 7%，两种最小相对误差相差14.397 5%。

同理应用粒子群算法(particle swan optimization,PSO)的支持向量机边坡预测模型[15]对左岸缆机平台边坡变形进行了二次预测，结果如图4所示。

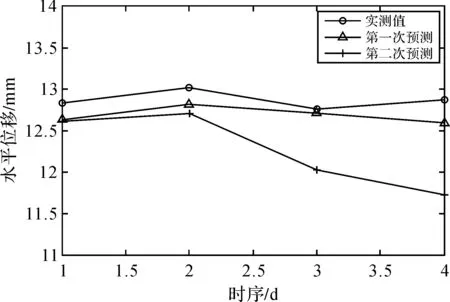
图4 PSO+SVR两次边坡位移预测

从图4中可知，基于粒子群算法的支持向量机边坡预测模型，两次预测值不同，证实了PSO参数寻优方法具有搜索结果随机性较大的特性，预测值不稳定性，需要多次训练才能确定较好的结果，不如本文改进网格法参数寻优结果稳定。

3 结 语

本文针对传统支持向量机参数寻优的不足，对网格法参数寻优作出改进，即在粗略搜索最优解大致位置的基础上，进行多次精细搜索，直至找到满足精度要求的解，在此基础上建立了改进的SVR大坝边坡位移预测模型。试验结果表明，该改进模型可应用到边坡预测中，与传统预测模型对比，稳定性和精度都有较大的提高，可以推广应用。

参考文献：

[1] 苏巧荣.基于MATLAB下BP神经网络的边坡稳定分析[J].河南大学学报(自然科学版),2007,31(6):595-600.

[2] 蒋晨,张书毕,文小勇.基于中位数回归分析的矿区变形监测数据处理[J].金属矿山,2016,479(5):192-195.

[3] 张拯,张献州.时间序列协整关系及其在变形分析中的应用研究[J].测绘工程,2015,24(9):53-58.

[4] 赵财军,陈鹏宇,李莉.改进GM(1,1)模型在基坑变形预测中的应用[J].人民长江,2010,41(6):32-34，39.

[5] 赵文秀,张晓丽,李国会,等.基于随机森林和RBF神经网络的长期径流预报[J].人民黄河,2015,37(2)：10-12.

[6] 赵洪波,冯夏庭.非线性位移时间序列预测的进化-支持向量机方法及应用[J].岩土工程学报,2003,25(4):468-471.

[7] 张玉欣,程志峰,徐正平,等.参数寻优支持向量机在基于光声光谱法的变压器故障诊断中的应用[J].光谱学与光谱分析,2015,35(1):10-13.

[8] 赵朝贺.一种改进的支持向量机参数优化方法[J].地理空间信息,2017,15(1):53-55，11.

[9] 李丹娜,郭云开,朱善宽,等.利用PRO4SAIL与支持向量机回归的组合模型反演植被等效水厚度[J].测绘通报,2017(8):50-55.

[10] 米兰,王文斌.基于支持向量回归机的汽轮机排汽焓预测研究[J].热能动力工程,2016,31(11):38-42.

[11] 郭美丽,覃锡忠,贾振红,等.基于改进的网格搜索SVR的话务预测模型[J].计算机工程与科学,2014,36(4):707-712.

[12] 杨学存,侯媛彬,洪卫林,等.基于参数优化支持向量机的煤泥输送管道压力预测[J].煤炭工程,2013,45(12):112-115.

[13] 郭际明,王威,张帅.支持向量机辅助下的智能手机行人运动模式识别[J].测绘通报,2018(2):1-5.

[14] 郑志成,徐卫亚,等.基于混合核函数PSO-LSSVM的边坡变形预测[J].岩土工程,2012,33(5):1421-1426.

[15] 高昆仑,刘建明,徐茹枝,等.基于支持向量机和粒子群算法的信息网络安全态势复合预测模型[J].电网技术,2011,35(4):176-182.