多系统融合全球电离层建模研究
王 健,党亚民,王 虎,张龙平,刘宗强,韩恒星(1. 山东科技大学测绘科学与工程学院,山东 青岛 66590; . 中国测绘科学研究院,北京 100830)
2000年美国取消SA政策以后,电离层延迟误差成为影响GNSS导航定位精度的最显著误差源,并给卫星通信等科研应用领域带来了不可忽视的影响。消除电离层延迟误差始终是电子通信及导航定位领域研究的热点问题。IGS(International GNSS Service)经过多年努力于2003年正式向全球科研机构提供GNSS原始数据及高精度数据产品,目前,美国JPL、欧洲CODE、ESA、UPC共4家分析中心从事全球电离层延迟日常数据的处理和产品发布[1]。在国内GNSS连续运行站的数据处理与分析方面的工作起步相对较晚但发展迅猛[2-3]。特别是近年来我国在GNSS基础设施建设、分析中心建设及数据处理技术方面都取得了令人瞩目的成绩,其中武汉大学iGMAS分析中心、上海天文台iGMAS分析中心、中国测绘科学研究院iGMAS分析中心等数十个分析中心陆续涌现。在中国,袁运斌、耿长江、章红平、韩文慧、王虎等学者开展了对电离层延迟建模方法的深入研究,为全球电离层精细建模研究提供了基础设施和技术思想支持。文献[4]就当前IGS站分布下,GLONASS数据改善了全球电离层模型化效果且卫星DCB稳定性优于接收机DCB。文献[5]融合BDS/GPS/GLONASS三系统建立电离层延迟模型并进行全球电离层反演试验,最后得到了有益结论。但当前仍需要学者对电离层进行努力探索,本文以此为基础,采用中国测绘科学研究院iGMAS分析中心数据对多系统电离层建模进一步研究,以便更好地为导航定位服务。
1 全球电离层延迟模型
1.1 测定测站上方电子含量
电磁波从卫星向地面传播经过电离层,由于电离层折射,不同频率的电磁波在传播过程中速度会发生变化[6-7]。对于同一频率的电磁波,在电离层中传输的相速度Vp和电离层的相折射率np,表示为[8]
(1)
式中,c为真空中的光速;np为相折射率,与电离层电子密度Ne、地磁场密度H0及质量m有关。
一般相折射率np可近似表示为
np=1-40.28Nef-2
(2)
式中,f表示载波相位的频率。代入式(1)并以二项式级数展开,略去二阶微量可得
vp=c(1+40.28Ne·f-2)
(3)
在量测距离时,测距码作为一个整体。沿卫星信号传播的轨迹s对电离层中电子密度进行积分,然后线性化并略去微小项,最后可得
(4)
式中,后一项就是测距码电离层的延迟量。
在实际测量时还需要考虑卫星和接收机的差分码偏差(differential code bias,DCB)的影响。由双频P码可得
(5)
式中,P1、P2为伪距测量值;f1、f2为双频载波相位频率;STEC为倾斜路径的总电子含量,计量单位为TECU;B为接收机和卫星的组合差分码偏差。
对于同一电离层,测站到各个卫星的传播路径不同,因此不同方向上具有不同的TEC值,其中,天顶方向的总电子含量VTEC的值是最小的[9-10]。一般采用单层电离层投影函数将无线电信号传播方向上的电子含量STEC投影到天顶方向得到VTEC,公式为
(6)
式中,VTEC表示垂直方向电离层电子含量;z′表示卫星在穿刺点(假设电离层压缩为一个单层,所有电子都位于该层,称为中心电离层。卫星传播路径与中心电离层的交点称为穿刺点IPP)处的天顶距;z为接收机处的天顶距;R为地球半径;H为假设的电离层薄层厚度。
1.2 建立全球电离层延迟模型
本试验采用CODE分析中心的球谐函数模型,采用15阶次的球谐函数模建立全球电离层延迟模型,并采用日固地磁参考系。根据电离层的周日变化特性,TEC值在时间域内采用分段线性函数表达[11-12]。具体公式为
bijsin(jλ))
(7)
式中,ρ为电离层穿刺点IPP的地理纬度;λ为电离层穿刺点IPP的日固经度;imax为球谐函数的最高阶数;j为球谐函数的阶数;Pij(cosρ)=Nij·Pij(cosρ),表示i度j阶的缔合勒让德多项式;Nij为归化函数某时刻的aij和bij。
结合式(5)、式(6)、式(7)可得
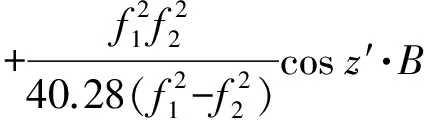
(8)
2 数据处理与分析
2.1 数据选取
国际GNSS监测评估系统(international GNSS Monitoring & Assessment System,iGMAS)是对北斗卫星导航系统BDS运行状况、主要性能指标进行检测和评估,生成高精度星历、卫星钟差、地球定向参数、跟踪站坐标和速率、全球电离层TEC格网等产品的信息平台[13]。中国测绘科学研究院是参与iGMAS分析中心建设的研究单位之一,全程参与系统测试与试运行。
本文试验数据皆来自中国测绘科学研究院北斗分析中心(CASM),共计400多个分布均匀的测站,其中包括iGMAS站、MGEX站和IGS站。测站大部分分布在北半球,南半球特别是海洋区域分布较少且不均匀。
2.2 处理策略与流程
本试验采用前一天、当天、后一天共3天的GNSS跟踪站观测数据,一起进行解算,这种综合处理可保证产品天与天之间的连续性。其中卫星和接收机的差分码偏差作为一个常数进行估计,并选定约束条件为所有卫星差分码偏差总和为零。
2.3 精度分析
2.3.1 格网TEC分析
CODE分析中心每2 h发布一组高精度的全球电离层格网数据(global ionosphere map,GIM),该文件可形成2.5°×5°的TEC格网图,通常作为同类研究的标准。以CODE分析中心发布的GIM产品为参考,利用本试验解算的全球电离层结果与CODE产品比较,进行精度分析。本试验采用2017年年积日199、200、201的GNSS观测数据进行解算,生成年积日200的电离层产品。限于篇幅,图1为UTC时间4:00、12:00、20:00的三系统电离层建模结果与CODE的差值图。
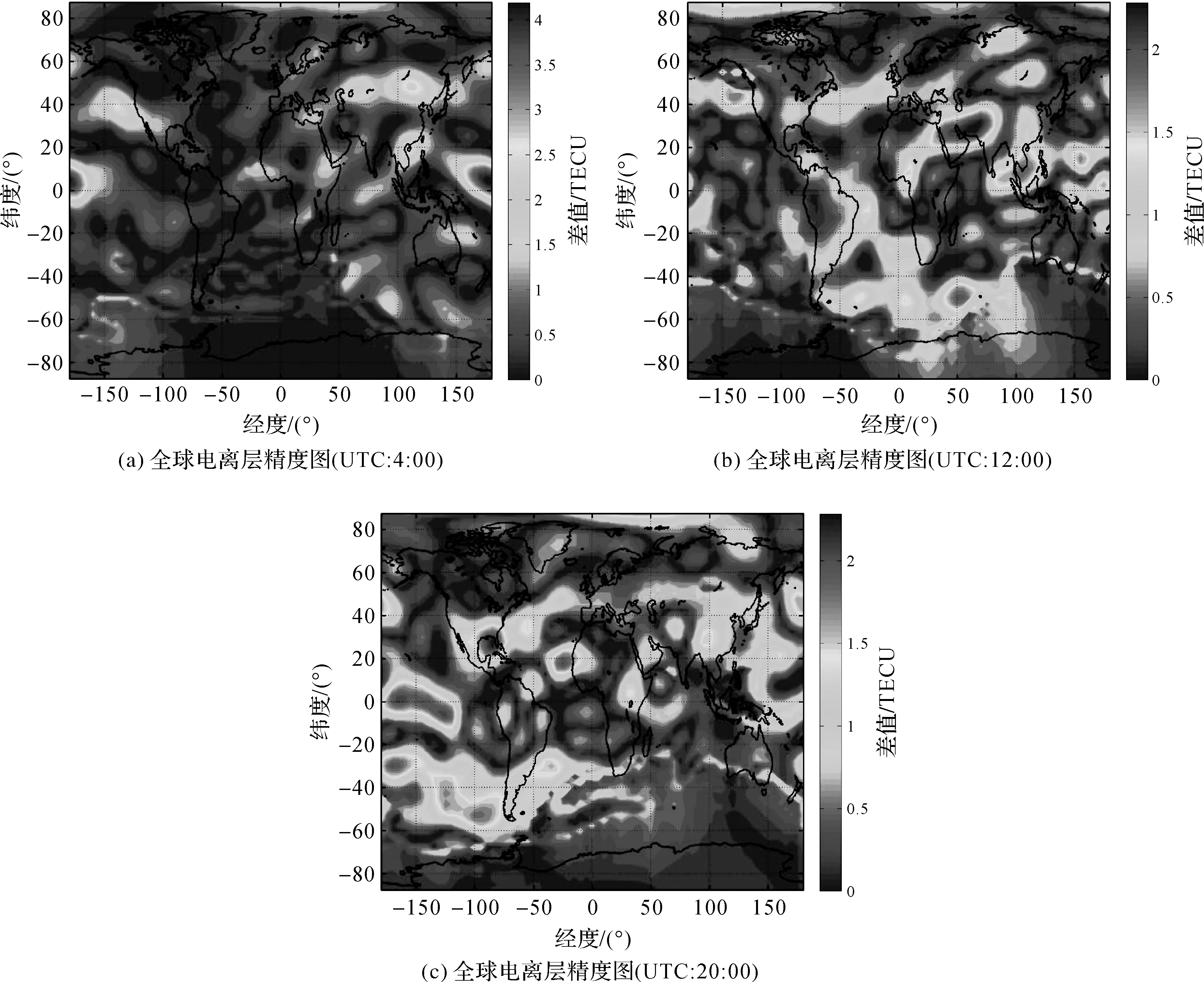
图1 电离层建模结果与CODE的差值图
由图1可以看出,本试验解算的三系统全球电离层结果与CODE产品的差值基本在0~1.5 TECU左右,精度较高,主要在测站分布比较均匀的大陆地区;某些区域的差值达到2~3 TECU,精度较差,主要分布在海洋地区,原因是站点少,测站分布不均匀。由此可知,除去精度略差的海洋区域,在其他地区,多系统融合全球电离层建模结果能较精确地表达电离层VTEC。
采用2017年年积日199—207共9 d GNSS观测数据生成一周的电离层产品进行精度分析,结果如图2所示。结果显示:北半球高纬地区精度均在0.6 TECU以内,北半球中纬地区精度均在0.6 TECU以内,北半球低纬地区精度均在2.2 TECU以内;南半球高纬地区精度均在0.8 TECU以内,南半球中纬地区精度均在1.5 TECU以内,南半球低纬地区精度均在2.1 TECU以内;低纬地区精度比中高纬地区精度差,说明该地区电离层较活跃,这与太阳活动有关;北半球中高纬地区比南半球中高纬地区精度略高,全球精度均在2.2 TECU之内。

图2 电离层产品与CODE产品对比结果
综上可知,本试验解算的电离层产品与CODE产品有较好的一致性,表明本次解算得到的电离层结果质量可靠。
2.3.2 测站建模残差
通过GNSS观测站获得站星视线方向的TEC信息,并利用投影函数将其转化为交叉点的VTEC;基于电离层TEC产品也可得到对应交叉点处的VTEC,统计二者差异,分析三系统融合全球电离层TEC产品的精度,公式为[14]
(9)
(10)
式中,bias与RMS分别为模型值与观测值之差的平均偏差与标准差;TECm,n、TECg,n分别为GNSS基准站TEC观测值和TEC模型值;mfn为电离层投影函数值;N为该测站在时段内的有效卫星总数。
图3给出了本次试验在2017年年积日200的全球426个测站TEC模型值与TEC观测值的平均偏差与标准差,由图3可以看出,各个测站TEC平均偏差基本在0左右波动,并且大部分在正负1.0 TECU之内,说明多系统融合全球电离层建模结果能较精确地刻画TEC变化,没有出现明显的系统偏差;各个测站TEC差值的标准差大部分在0~3 TECU以内,且最大不超过6 TECU,说明多系统融合全球电离层建模结果的精度符合要求且比较稳定。
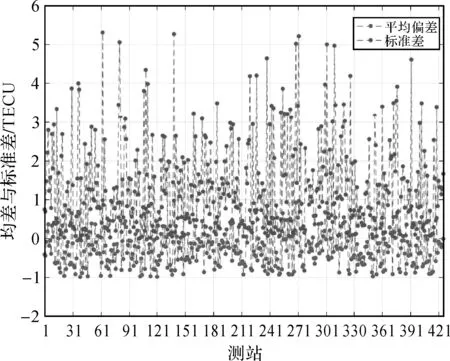
图3 426个测站建模残差的平均偏差与标准差
2.3.3 差分码偏差DCB精度分析
卫星差分码偏差DCB作为电离层TEC建模的中间产品,每天都可以获得卫星和接收机的DCB产品估值, 其稳定性和精度可在一定程度上反映电离层模型精度[15]。本试验同时计算2017年182—212共31 d三系统融合的差分码偏差,并分析2017年7月卫星差分码偏差精度。
以IGS发布的卫星差分码偏差为参考,统计不同卫星相对于参考值的偏差。结果如图4所示,其中图4(a)表示GPG系统C1P2差分码偏差,图4(b)表示GLONASS系统C1P2差分码偏差,图4(c)表示BDS系统B1B2差分码偏差。可以看出:GPS卫星系统C1P2码偏差均小于1 ns,大部分在0.5 ns以内,精度最高;GLONASS卫星系统C1P2码偏差均小于2 ns,精度比GPS系统略低;BDS卫星系统B1B2码偏差均小于1 ns,精度比GLONASS系统略高,但不如GPS系统稳定,码偏差随年积日变化较大,可能是BDS系统星座结构不完善的原因。
3 结 语
本文采用中国测绘科学研究院iGMAS分析中心数据进行三系统融合全球电离层延迟建模试验,得到如下结论:
(1) 除去精度较差的海洋区域,在大陆地区,多系统融合全球电离层建模结果能较精确地表达电离层VTEC,且本试验解算的电离层产品与CODE产品有较好的一致性,表明本次解算得到的电离层结果质量可靠。
(2) 多系统融合全球电离层建模结果能较精确地刻画TEC变化,没有出现明显的系统偏差,建模结果的精度符合要求且比较稳定。
(3) 对比三系统差分码偏差DCB的精度统计结果,GPS卫星系统C1P2码偏差均小于1 ns,大部分在0.5 ns以内,精度最高;GLONASS卫星系统C1P2码偏差均小于2 ns,精度比GPS系统略低;BDS卫星系统B1B2码偏差均小于1 ns,精度比GLONASS系统略高,但不如GPS系统稳定,码偏差随年积日变化较大,可能是BDS系统星座结构不完善的原因。
致谢:感谢国际GNSS监测评估系统(iGMAS)中国测绘科学研究院提供的数据和技术支持!
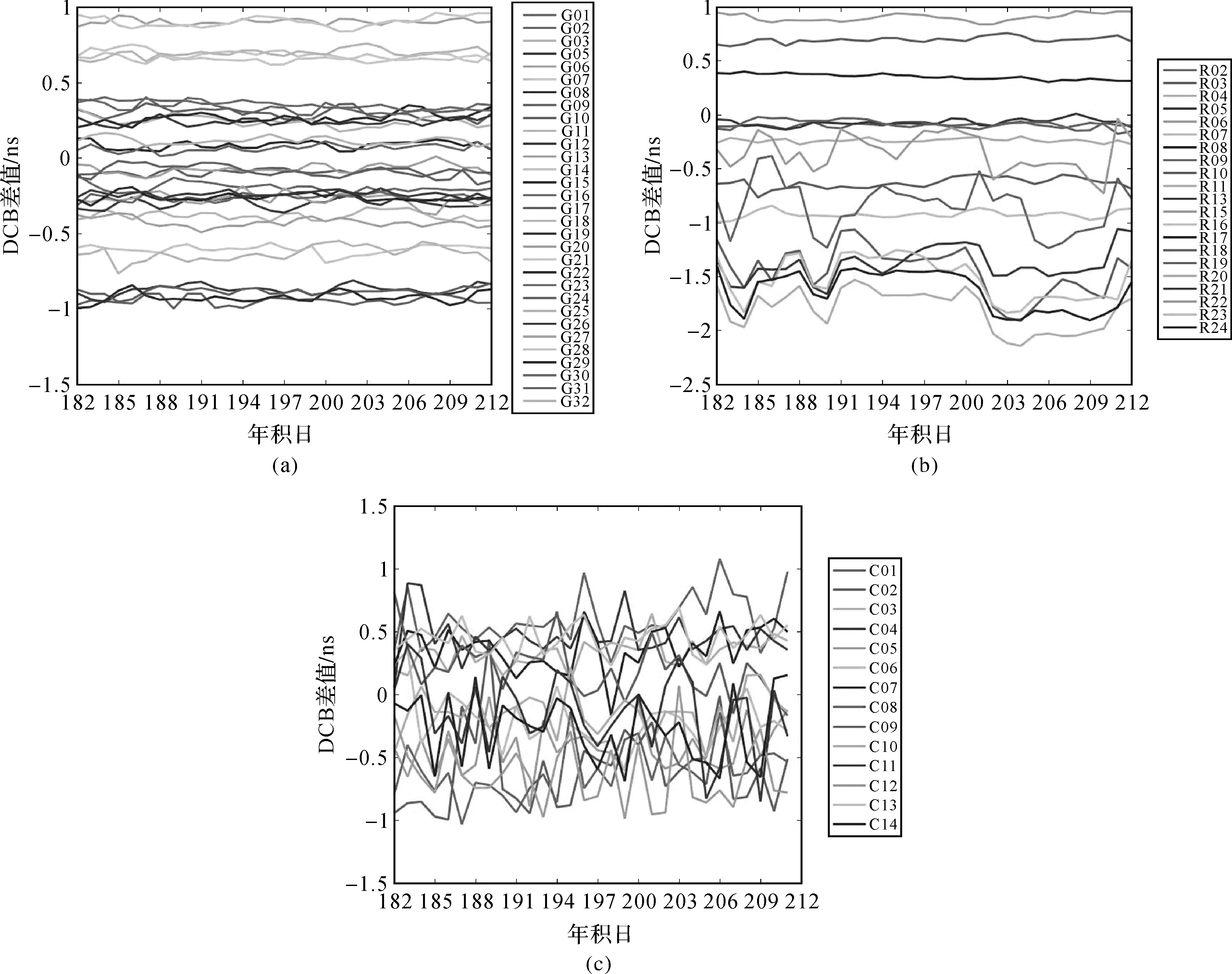
图4 三系统卫星差分码偏差精度结果
参考文献:
[1] SCHAER S.Mapping and Predicting the Earth’s Ionosp-heric Using the Global Positioning System [D].Swizerland: Astronomical Institute of the University of Bern,1999.
[2] 耿长江.利用地基GNSSS数据实时监测电离层延迟理论与方法研究[D].武汉:武汉大学,2011.
[3] 张小红,李征航,蔡昌盛.用双频GPS观测值建立小区域电离层延迟模型研究[J].武汉大学学报(信息科学版),2001,26(2):140-143.
[4] 章红平,韩文慧,黄玲,等.地基GNSS全球电离层延迟建模[J].武汉大学学报(信息科学版),2012,37(10):1186-1189.
[5] 党亚民,王虎,赵文娇,等.融合BDS/GPS/GLONASS反演全球电离层特性研究[J].大地测量与地球动力学,2015,35(1):1-5.
[6] 章红平,施闯,唐卫民.地基GPS区域电离层模型与硬件延迟统一解算分析[J].武汉大学学报(信息科学版),2008,33(8):805-809.
[7] 袁运斌.基于GPS的电离层监测及延迟改正理论与方法的研究[D].北京:中国科学院研究生院,2002.
[8] ZOU L, RISHBETH H, MULLER C F, et al.Annual and Semiannual Variations in the Ionospheric F2-layer:I.Modeling[J].Annales Geophysicae,2000, 18(8):927-944.
[9] 王虎.地基和空基GPS电离层反演技术的研究及其应用[D].上海:同济大学,2012.
[10] 唐卫民.GPS载波相位平滑伪距精度分析与应用探讨[J].测绘信息工程,2005,30(3):37-39.
[11] 耿长江,章红平,翟传润.应用Kalman滤波实时求解硬件延迟[J].武汉大学学报(信息科学版),2009,30(11):1309-311.
[12] 王虎,王解先.基于GPS技术实时监测2009年7月22日日全食长三角区域电离层TEC变化[J].地球物理学报,2011,54(7):1718-1726.
[13] 郭东晓,党金涛,李建文,等.iGMAS全球电离层延迟模型及并行计算策略[J].测绘科学技术学报,2015,32(4):357-360.
[14] 王成,王解先,段兵兵.附有国际参考电离层约束的全球电离层模型[J].武汉大学学报(信息科学版),2014,39(11):1340-1346.
[15] 余明,郭际明,过静珺.GPS电离层延迟Klobuchar模型与双频数据解算值的比较与分析[J].测绘通报,2004(6):5-8.

