两矿之间散体边坡二次剥离及角度优化研究

周 游

(1.煤炭科学技术研究院有限公司安全分院，北京市朝阳区，100013；2.煤炭资源高效开采与洁净利用国家重点实验室(煤炭科学研究总院)，北京市朝阳区，100013)

露天开采作业过程中，覆盖物的剥离和排弃形成了大型的排土场岩土构造工程。由于剥离过程中的松碎和挖掘作业造成了原始岩层的打乱和混合，统一排弃至排土场之后，混合物料呈散体状态在排土场堆载形成一定强度的岩土混合物。散体边坡的强度不同于原岩边坡的强度，并且在堆载过程中不断变化，其强度将决定边坡稳定性及露天矿安全生产。

为了研究黑岱沟露天煤矿转向期间内排土场散体边坡的稳定性，并设计合理的散体边坡角度，为准确期间坑内的人员设备安全和作业空间提供足够的技术保障，本项目采用现场原位测试、室内试验、数值模拟相结合的综合性研究方法，针对黑岱沟露天煤矿排土场堆积散体的自然安歇角度与散体颗粒之间的函数关系及其力学特性进行深入系统的研究，给出经济合理、安全可靠的散体边坡角度。同时，对排弃物料特别是大块岩石滚落规律进行研究，圈定大块岩石的滚落范围。

对于不同强度的重塑压力与重塑岩体抗剪强度之间的函数关系，以及重塑时间长短对于重塑岩体强度的影响规律尚不明确，本次研究借助实验室和现场试验测定不同重塑压力及不同重塑时间的重塑岩体的抗剪强度，揭示它们之间存在的函数关系，并对露天矿排土场稳定性分析进行改进和完善。

1 散体物料堆载变形及力学强度研究

1.1 散体堆载过程沉降量

对于不同粒径的散体物料在排土场混合排弃，在不同的垂向压力(堆载高度)条件下，散体物料表现出不同程度的压密固结。相同高度的台阶在排土场进行堆载所呈现的堆载压力为均布荷载，在此条件下，任一垂直截面都是荷载的对称面，且侧向应变为零，即x=y=0。侧向应力对称相等，存在如下关系：

(1)

式中：σx——x方向应力，kN；

σy——y方向应力，kN；

σz——z方向应力，kN；

μ——泊松比。

根据散体物料综合的变形模量E0和泊松比μ这两个弹性常数，可得到物料的垂向应变为：

(2)

将式(1)代入式(2)可得：

(3)

在均匀荷载σz的作用下，散体物料会产生沉降，对于高度为h的散体物料，其沉降值S为：

(4)

由此可知，随着垂向压力(堆载高度)σz的增加，z向应变量εz和沉降量S均呈线性增长。散体物料重塑存在孔隙压密和排水过程，这一过程所需的时间长度因岩性不同而异；对于粘性土，需要很长一段时间完成排水固结；对于砂质土，则只需要很短时间便可完成重塑过程中的排水固结。

1.2 散体物料长期堆载后的强度测试

为了准确测定散体物料堆载之后的综合物理力学参数，本研究采用原位试验进行抗剪强度测试，原位测试的是大型岩土试样的力学指标，即岩土层保持原状态不变时，测定岩土的工程力学性质指标。

按照选定的原位试验测试点，将试验样品制备成1 m3岩块，在左右两侧距离中心各1.4 m处，分别安装1根预应力锚索，锚索上安装有垂压承载工字钢梁，工字梁和岩样顶面之间安装1个垂压千斤顶，最大可施加10 t的垂向荷载。平行于工字钢梁的岩样两个侧面，选择其中1个作为剪切面，在剪切面、剪切基础面以及岩样顶面各放置1块1 m2的承压钢板，剪切力由4个同型号的千斤顶同时施加，4个千斤顶在剪切面等间距放置，在最外侧的两个千斤顶上各固定1个千分表，以记录岩样的剪切位移。所有的设备安装完毕，并调试好之后，依次进行多个测试点的原位实验。

原位试验点1总共施加了4级垂直荷载，分别是23 kPa、40.95 kPa、51.43 kPa和61.9 kPa，得到的剪应力—剪应变曲线如图1所示。

图1 原位试验点1的剪切位移曲线

与各级正压力对应的最大剪应力分别是19.20 kPa、23.04 kPa、34.56 kPa和38.40 kPa。根据正压力与剪应力的关系，得到图2所示的正压力—剪应力曲线。

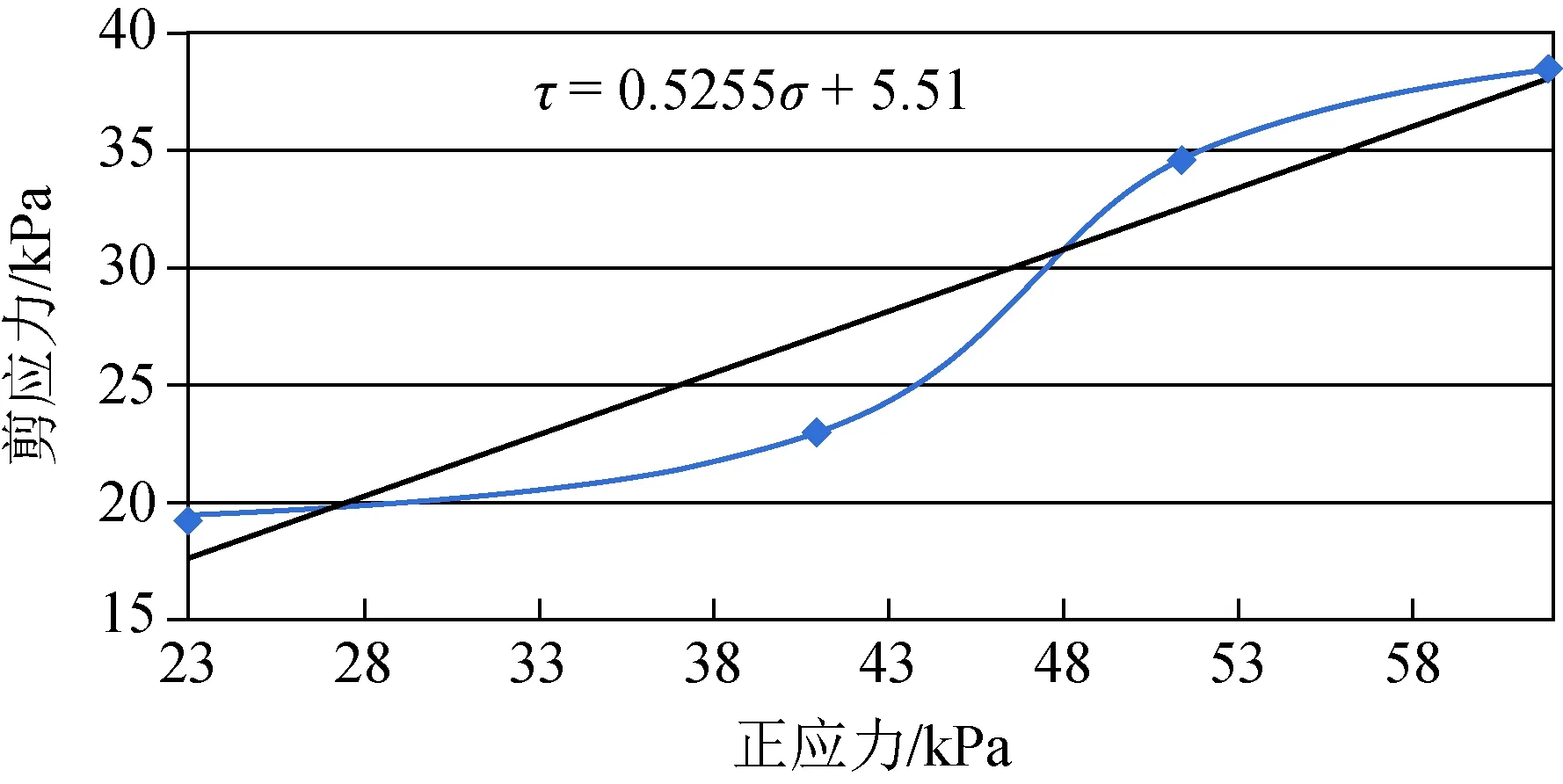
图2 原位试验点1的正压力-剪应力曲线

由图2可以得出原位试验点1的抗剪强度参数为：粘聚力C=5.51 kPa，内摩擦角φ=27.72°。

综合多组原位试验结果得到散体边坡的物理力学参数如表1所示。

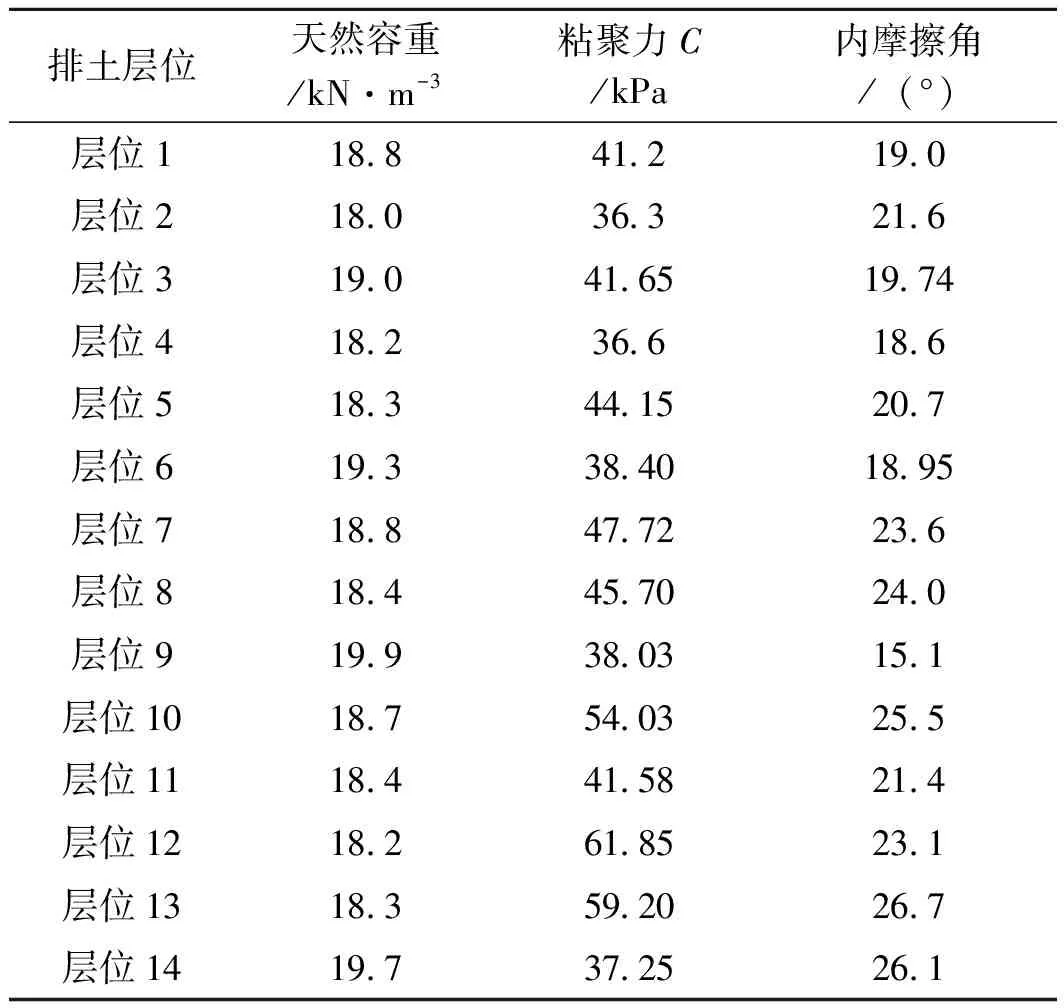
表1 排弃物的主要物理力学参数原位测试

2 两矿之间散体边坡稳定性分析及结构优化

2.1 散体边坡稳定性分析

黑岱沟露天矿从首采区转到二采区后，二采区工作线与哈尔乌素矿露天工作线出现平行推进的状况。哈尔乌素矿的推进位置超前黑岱沟矿5年左右，即在哈尔乌素矿刚压帮内排后，黑岱沟矿就要进行二次剥离，从经济角度考虑不合理。若哈尔乌素矿内排时能够为黑岱沟矿二采区开采时留沟，黑岱沟矿的二次剥离量就会减少。哈尔乌素矿的推进位置超前黑岱沟矿，按照现状推进进度，哈尔乌素矿内排土场上部台阶恰同黑岱沟矿采场上部台阶共线。哈尔乌素矿压帮留沟物料排弃完成后，很快又由黑岱沟矿进行剥离，最终黑岱沟矿形成松散岩体端帮边帮。

2.1.1 边坡稳定性分析模型构建

黑岱沟露天煤矿采场一侧端帮坡为非松散体帮坡，有足够的稳定性。可能出现稳定性问题的是左侧由松散体堆积形成的帮坡。其上部水平长时间暴露，松散体会出现大幅度沉降以及其他方面的变化，下部水平一段时间后重新开挖，对上部水平存在扰动，上部水平连接下部水平形成高台阶帮坡，稳定性必须分析，所以模型构建主要是针对断面左侧部分。为分析松散岩体边坡破坏机理，选用FLAC软件对上述断面进行数值模拟分析，模型如图3所示。模型边界条件为底部边界固定，左右两侧边界水平方向位移约束，采用平面应变模型假设。在数值计算中，岩体变形破坏遵循摩尔-库伦强度准则。

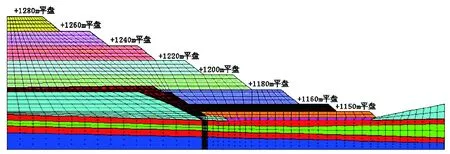
图3 FLAC3D数值模拟模型

2.1.2 整体边坡变形破坏机理分析

为真实、准确地模拟松散岩体在内排土场堆载的过程，在数值模拟中，内排土场的若干排土台阶逐级堆载，每次堆载产生的不平衡力会对散体物料进行逐级加载，造成不同区域的岩体力学参数差异较大。通过分析得到松散岩体边坡稳定系数为1.29，其剪应变情况以及位移矢量分布如图4所示。由图4可以看出，边坡位移量最大位置位于排土场后方，表现为竖直方向的沉降，排土场底部台阶位移矢量指向右，说明边坡底部台阶有水平向右的滑动趋势，但是受排土场前方反坡的压脚作用，位移量较小，在合理范围之内。结合边坡变形矢量方向中可以看出，边坡堆载至+1240 m平盘时上部台阶仍在变形，变形方向以竖直向下的沉降为主，变形速率极小可忽略不计，排土场底部台阶变形已经完成。

图4 剪应变增量云图及位移矢量图

由于边坡堆载，引起应力重分布，边坡周围应力迹线发生明显偏转，其总体特征表现为愈靠近临空面，应力愈接近平行于临空面。由于受到上部排弃物料的作用，在排土场基底后方竖直应力较大，但边坡其他位置水平应力和竖直应力均较小，没有出现应力集中现象。边坡整体失稳将发生于强度软弱带或应力集中区，该部位松散体单元将产生不同程度的不可恢复的塑性变形，若发生塑性变形的软弱带或应力集中区相互贯通，则表明边坡内将在相互贯通的剪切破坏面发生整体失稳。采场塑性区分布如图5所示。由图5可以看出，排土场基底后方基岩由于上部载荷较大，产生部分压剪破坏，但破坏范围不大，对边坡整体的稳定性影响较小。

图5 塑性区分布图

在排土场基底煤层底板软岩层中出现的剪切应变较大，且产生大量压剪破坏，在排土场内部有向上发展的趋势，但是塑性区并未贯通形成连续的滑面。对边坡变形的分析可知，边坡变形基本已经完成，所以边坡下部台阶的塑性破坏并不会继续发展，因此可以判断当排土场堆载至+1240 m平盘时，边坡整体是稳定的。

2.2 边坡结构优化

由于端帮角度决定条区的二次剥离量，从而进一步影响矿区的平均剥采比，因此提高端帮边坡角度可以很大程度上降低两矿之间的二次剥离量。基于这一思路，对散体边坡角度进行优化，研究其可以保证安全生产的最大安全角度。

2.2.1 南端帮二次剥离边坡角度优化

黑岱沟矿转向期间，涉及的散体边坡有两大类：一类是剥离物内排形成的排土场松散边坡，另一类是对哈尔乌素矿内排土场二次剥离揭露的散体边坡，这两类散体边坡的存在时间不同，沉降效果不同，胶结程度差异较大。由于哈尔乌素矿二次剥离物的排弃时间较长，软、硬岩交互重塑及胶结状态要明显优于内排土场散体边坡，能够保持较大角度状态下的短期稳定，结合分析结果，确定其单一台阶边坡角度为45°，在此基础上进行南端帮散体边坡整体角度的优化，通过不断的调整端帮边坡角度得到散体边坡稳定系数随角度的变化曲线如图6所示。

2.2.2 北端帮帮内排散体边坡

北端帮内排台阶为转向前首采区正常推进过程中的主要内排土作业区，其松散程度远大于南端帮，根据二维和三维模拟结果，充分考虑结构优势，确定北帮内排土场的台阶边坡角为40°，通过不断调整北端帮整体角度，得到其最佳边坡角度为23°。稳定系数变化规律如图7所示。

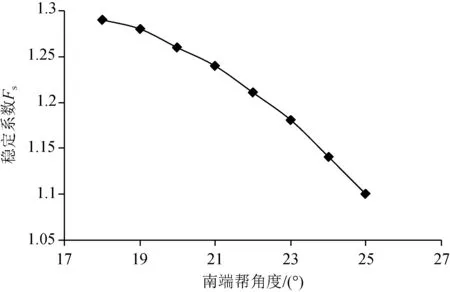
图6 南端帮二次剥离边坡不同角度所对应的稳定系数

图7 北帮边坡散体边坡不同角度所对应的稳定系数

通过对南、北端帮散体边坡角度的优化，得到了南端帮的最佳角度为25°，北端帮的整体角度为23°，按照这些参数进行开采，可以保证两个端帮边坡在开采期间的安全稳定，同时能保证矿山剥采比达到最佳值，对于矿山整体经济效益较为有利。

3 结论

黑岱沟与哈尔乌素露天矿共用端帮为排土场散体物料经二次剥离之后形成的高陡边坡，北端帮为内排形成的散体边坡，采用原位试验测定散体物料的物理力学参数，然后借助FLAC数值模拟评价边坡稳定性，并进行边坡角度优化，得到以下结论：

(1)南端帮为哈尔乌素内排土场二次剥离形成的散体边坡，开采现状的

稳定系数为1.29，通过角度调整可达到的最佳角度为25°。

(2)北端帮为黑岱沟内排土场形成的散体边坡，初始稳定系数为1.30，通过角度调整得到其最佳角度为23°，对应的稳定系数为1.10。

(3)优化后的南、北端帮散体边坡角度可以保证露天矿的安全生产，并且可以实现在矿区的整体剥采比达到最优。

参考文献：

[1] 才庆祥，周伟，舒继森等.大型近水平露天煤矿端帮边坡时效性分析及应用[J].中国矿业大学学报，2008(6)

[2] 刘勇，车兆学，李志强等.露天煤矿端帮残煤开采及边坡暴露时间分析[J].中国矿业大学学报，2006(6)

[3] 缪林昌，崔颖，陈可君等.非饱和重塑膨胀土的强度试验研究[J].岩土工程学报，2006(2)

[4] 黄英豪，朱伟，张春雷等.固化淤泥重塑土力学性质及其强度来源[J].岩土力学，2009(5)

[5] 王亮，谢健，张楠等.含水率对重塑淤泥不排水强度性质的影响[J].岩土力学，2012(10)

[6] 熊承仁.重塑非饱和粘性土的强度习性研究[D].中南大学，2005

[7] 郭长宝，张永双，孟庆伟等.重塑硅藻土抗剪强度的环剪试验研究[J].岩土力学，2013(1)

[8] B Dolinar, L Trauner.The impact of structure on the undrained shear strength of cohesive soils[J].Engineering Geology，2007(1)

[9] S Vithana, S Nakamura, S Kimura, et al.Effects of overconsolidation ratios on the shear strength of remoulded slip surface soils in ring shear[J].Engineering Geology, 2012(2)

[10] B Tiwari, B Ajmera.New Correlation Equations for Compression Index of Remolded Clays[J].Journal of Geotechnical and Geoenvironmental Engineering, 2012(6)

[11] P Vinod, A Sridharan, K Deepa, et al.Discussion: remoulded shear strength at plastic and semi-solid states[J].Geotechnical Engineering, 2013(5)