以平面向量最值为例谈学生解题思维能力提升的策略

浙江安吉县孝丰高级中学 (313301) 张忠潮

自浙江省采用新高考后，高三数学复习时间显得尤为紧张、任务更加重，从而使得二轮复习显得较为仓促.如何合理精选习题、科学设计教学、通过习题教学提升高三复习效益，是每一位高三一线教师认真思考的一个课题.

在高三教学中，教师要强调数学知识发生、发展过程体验，发现问题、提出问题，注重数学知识的再发现、再创造过程.因此，数学课堂教学设计要学会借题发挥，目的是让难以解决的问题扩大其“最近发展区”，为顺利解题做好铺垫，为学生搭建思维的脚手架，让学生尝试成功的喜悦，同时调动学生探究的积极性，以此提升高三数学复习效益.本文以《平面向量最值的求法》复习课为例，谈谈怎样由习题去提升学生的解题思维能力.

一、借问题情境，追本溯源

波利亚先生说过：“有些题目的解答就像魔术师帽子里的兔子，不知道从哪里冒出来的，这些想法是如何想到的？揭示了这类问题的本质，我们就能站在更高位置来看待这个问题，问题就迎刃而解.”

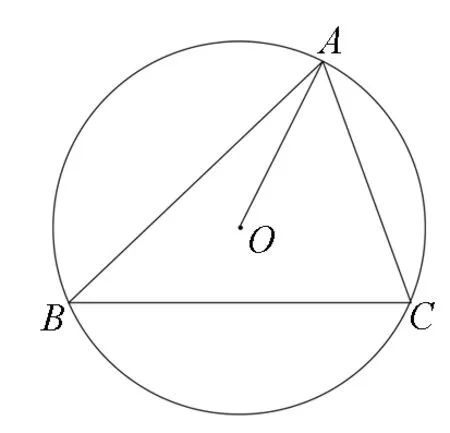
图1

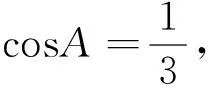
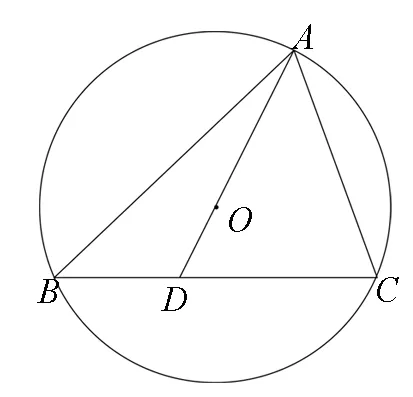
图2

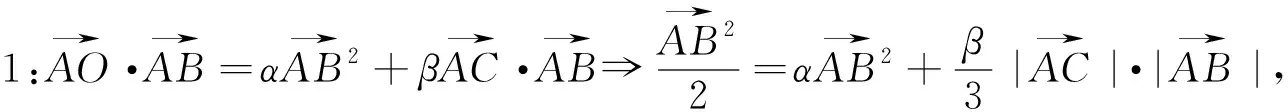
师：学生感觉这类问题难度较大，那么它们的解决方法除了上面几个学生提供的方法外，到底有无规律可循？这类问题是否隐含着一定的背景？它们是如何由简单到复杂演变的？

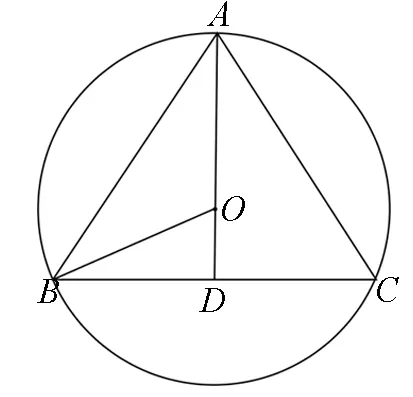
图3

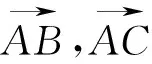
师：很好，那同学们能利用变量α,β来表示吗？

师：生2，你能继续解决此题吗？

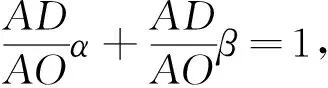
设半径OA为定值，只需求OD最小即可.当OD最小，即OD⊥BC，α+β最大，此时AB=AC.

师：问题本质是什么呢？事实上，这类问题来源是人教A版P94平面向量基本定理：

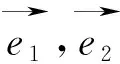
但是平时的考察，更多的时候以考察它的推论为主，即三点共线结论：

图4

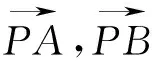
二、借一题多解，发散思维

在数学教学中通过一题多思，一题多解，一题多讲，可以巩固学生知识，训练学生思维，开拓学生视野.用多角度去看一道题，强化思维的连贯性，知识的衔接，能全面利用所学知识解决实际问题，培养学生对知识的活学活用有重要帮助.

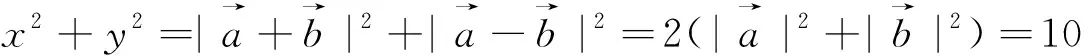
图5

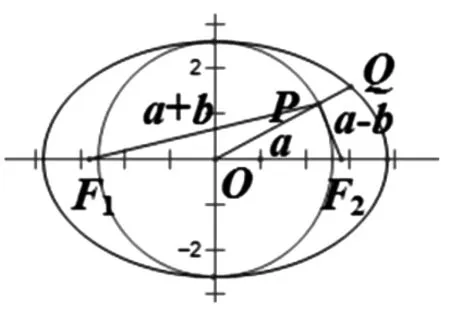
图6

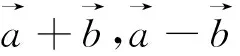
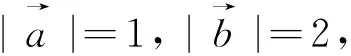
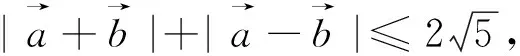
点评：向量是近代数学中重要和基本的数学概念之一，它是沟通代数、几何和三角函数的一种工具，有着极其丰富的背景.本题以向量的模的计算为背景，考查了向量的和与差的几何意义，考查了函数的最值及其几何意义，考查了数形结合的能力，涉及基本不等式、线性规划等基本知识.从所求结论看本题考查函数最值问题，如何利用化归思想实现等式和不等式之间的转化是解决本题的关键，也是解决本题的难点.

三、借多题归一，感悟本质

一题多解对锻炼学生思维与解题的灵活性固然有很多益处，但教师在教学中也应注意要一题多解，多解归一，从而提炼出解决多道同类题目的方法，形成多题一解.

诚然，通过“一题多解”训练，可培养学生根据不同的思路，应用不同的基础知识，采取不同的数学方法，灵活解答同一个问题的能力.然而，目前大多数学生基础较差，看到题目首先联想到的是类似题目的一种通解或通用的解题模式.多题归一就是利用这种心理，以通用模式套各种类似的题目，减轻学生的负担，且可以训练学生化归的思想，同时它对培养学生规范地书写解答题的解题过程也是一次强化性训练.下面通过一题多变的分析过程说明多题归一的益处.

点评：多解归一的教学中，如果有意识去分析和研究，是举不胜举的.拿到一个题目，如果深入去分析、解决与反思，必能以一当十、以少胜多.培养学生各方面技能，特别是自主探索，创新思维的能力，也就无需茫茫的题海了.教学是为了让学生学会看到一道题就想到一类题，想到相应解法，才是正道.所以教师要不断从这方面入手教学，通过一题多解，到一题多变、多题归一，最后整理总结，得到多题一解，让学生在紧张的做题过程中，看到一道题就知道怎么解.

四、借课堂教学，学会反思

1.在交流探究中暴露学生的思维过程

叶澜教授说：“课堂是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的因素，而不是一切都必须遵守固定路线而没有激情的行程.”课堂教学过程是复杂的、丰富多变的，难免会遇到超出预设方案之外的新问题、新想法，教师应该善待学生提出的“意外”问题，尊重学生的“话语权”，为学生营造一个敢于发表自己见解、勇于说出自己想法的平台，适时调整教学设计方案，为学生的“动态生成”腾出一片广阔的空间，并因势利导，借题发挥，提升复习效益.

2.在比较中优化学生的思维能力

只有比较才能辨别优劣，只有比较才能使学生掌握更适合自己的解法.一题多解就是在比较中进行的，其目的要明确：不是解法越多越好，而应该选择有助于提升学生思维能力、培养学生解题能力的解法.通过一题多解训练，可以优化学生的解题思路，从而达到快速找准解决问题的方法.因此，解法比较可以不断拓展学生的思维能力.

[1]姜晓洁，于兴江.一题多解与一题多究[J].中学数学研究(江西师大),2016(06):42-45.

[2]伊建军.玩转数形结合 提升数学思维[J].中学教研,2016(02):31-34.