基于人工免疫算法的微网需求侧响应优化调度

曹益飞, 高文根

(安徽工程大学检测技术与节能装置安徽省重点实验室， 安徽 芜湖 241004)

引 言

考虑需求侧响应的微电网优化配置技术已经成为当下国内外专家学者研究的重点[1-4]，在理论和实践方面取得了一定的成果。例如，文献[5]基于分时电价，建立分布式电源与需求侧负荷优化管理的协调运行模型；文献[6]以系统总运行费用和储能循环电量最小为目标，建立在分时电价和需求侧管理(Demand side maragement, DSM)机制下的光伏微电网多目标优化模型；文献[7]综合分析电动汽车充电、光伏发电及储能系统等多方面的运行特性，提出考虑购电费用和蓄电池循环电量的多目标优化调度数学模型；文献[8]提出了一种基于储能SOC状态的微电网能量优化调度策略，结合实时电价调整储能SOC状态实现用电成本最低。

综合上述研究成果，发现目前仍缺少电动汽车参与下基于人工免疫算法的微电网优化调度方法。本文在已有研究基础上，以实际光伏微电网工程为背景[9]，针对电动汽车(electric vehicle,EV)参与以及需求响应(demand response,DR)优化运行问题展开研究。在考虑分时电价的基础上，综合考虑购电费用和储能使用寿命[10-11]，建立多目标优化运行模型，采用人工免疫算法对模型进行求解。从微电网系统的角度出发，验证优化方法的可行性和有效性。

1 光伏微电网系统

由于光伏微电网机动性好、可控性强等优点，为其接入公网带来了很大的方便。本文研究的光伏微电网系统模型[12]如图1所示。系统主要组件功能有：(1)光伏电池组：由太阳能电池板串、并联组成，吸收太阳能并转换成直流电，是系统主要电源；(2)储能系统：由锂电池串、并联组成，主要作用是储能；(3)电动汽车充放电装置：主要作用是在停车时段内使电动汽车与微电网进行电能交换；(4)固定负荷(fixed load, FL)：主要电能消耗单元；(5)可转移负荷(transferable load, TL)：系统重要的调节单元，通过调节可转移负荷的用电时间，减小系统在用电高峰期购电的费用。各组件集中连接在公共交流母线上，并通过通信线路与微电网能量管理系统之间进行信息交换[13]，实现微电网内各个模块之间的协调与控制，是微电网优化运行控制的关键。

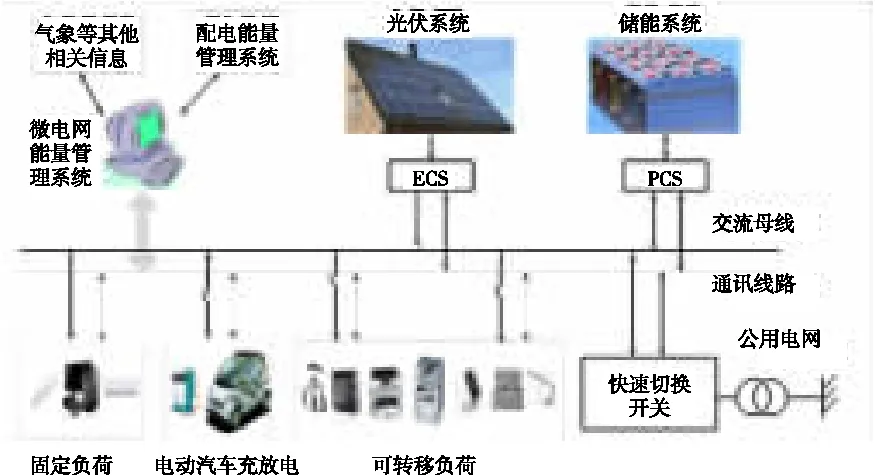
图1 考虑V2G的光伏微电网系统模型

2 微电网优化运行数学建模

2.1 系统运行策略

基于对光伏微电网拓扑结构的分析，建立相应的优化调度问题模型[14-15]，总体原则及假设条件如下：

(1) 光伏微电网中的负荷主要包括固定负荷、可转移负荷；假设负荷的运行特性已知，本文只考虑购电费用，不考虑向配电网售电；光伏发电成本、其余部分损耗费用及模块间的电能损耗均不考虑。

(2) 假设电动汽车锂电池为相同类型，且容量均相同，均满足储能系统的充放电功率和SOC约束，蓄电池充放电功率恒定，蓄电池荷电状态初始值为20%～100%的随机值；电动汽车在停放状态时保持与充电装置相连，以便优化运行时交换电量。

(3) 由于目前电动汽车普遍采用的是先恒流后恒压的充电方式，且一般情况下，恒流充电阶段是SOC增长的主要阶段，充电功率基本维持不变，所以本文以恒功率充电计算电动汽车充电功率。

2.2 目标函数建模

目标函数1：最大化储能使用寿命，即最小优化时间T内储能使用寿命的等效折损系数NT_sto最小[13]。

(1)

式中：n为时间T内储能系统的充放电循环次数；Ni为对应于储能第i次充放电循环的等效折损系数；f(SOCi)表示储能蓄电池第i次充放电的荷电状态为SOCi时，利用f函数求解其对应的等效折损系数。

目标函数2：光伏微电网系统购电费用最小，目标函数可以表示如下：

(2)

式中：F为购电费用；T为优化的时段数；Pg(t)表示t时段微电网从配电网购电平均有功功率；p(t)为t时段的电价。

2.3 约束条件建模

(1) 微电网功率平衡约束条件

根据微电网的实时功率平衡关系[16]，可得：

Pb(t)+PL(t)+Pev(t)=Ppv(t)+Pg(t)

(3)

式中：Pb(t)为t时段微电网蓄电池的充放电功率，充电时Pb(t)为正，放电为负；Pev(t)为t时段EV的充放电功率，电动汽车充电时Pev(t)为正，电动汽车放电时为负；Ppv(t)为t时段光伏发电功率，可由历史数据及其气象信息等进行预测；Pg(t)为t时段微电网与配电网交换的功率；PL(t)为t时段负荷侧的总负荷功率，包括固定负荷以及转移后的可转移负荷的功率，即：

(4)

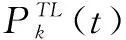
(2) 可转移负荷约束

可转移负荷约束可表示为：

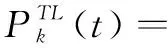
(5)

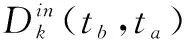
可转移负荷允许转移时间约束为：

(6)

式中：Sk为第k类可转移负荷允许转移的时间范围。

(3) 电动汽车充放电功率和时间约束

电动汽车充放电状态由用户设定、蓄电池荷电状态和微电网所需求的功率等因素决定，有：

(7)

(8)

(9)

(10)

另外为实现电动汽车的行驶需求，电动汽车使用时，蓄电池荷电状态不低于用户设定值，有：

SOCijde(t)≥SOCijde(set)

(11)

式中：SOCijde(t)为第j台待行驶电动汽车蓄电池第i次的荷电状态，SOCijde(set)为第j台待行驶电动汽车用户设定的蓄电池第i次的荷电状态。

(4) 储能蓄电池的充放电功率和SOC约束

储能系统包括系统储能蓄电池和电动汽车蓄电池[17]，其充放电功率受双向AC/DC功率变换器额定容量的约束，故应满足：

(12)

(13)

式中：Pc_rat和Ec_rat分别为储能系统的额定功率和额定容量；SOCmax和SOCmin分别是储能系统SOC的上限和下限。另储能系统的当前荷电量Ec(t)可通过下式递推得到，即:

(14)

式中：ηc是储能系统的充/放电效率；荷电量Ec(t)应满足：

Ec_ratSOCmin≤Ec(t)≤Ec_ratSOCmax

(15)

同时，由于每个优化周期的连续性，故要求每个优化周期的储能蓄电池初始SOC相同，即：

Ec(0)=Ec(T)

(16)

3 优化模型的求解方法

根据前文分析，本文以最大化储能使用寿命及与配电网的交换电量最小为目标，综合考虑微电网功率平衡约束、可转移负荷约束、电动汽车的充放电约束、储能荷电状态(SOC)等约束条件，将储能蓄电池的功率、可转移负荷的转移时间和转移量以及电动汽车的起始充放电时间和交换功率为决策变量，可将优化模型的待求解问题表示为：

(17)

采用人工免疫算法[18-20]对上述优化问题进行求解，算法的主要步骤如图2所示，优化目标函数的求解具体实施步骤可描述如下：

步骤2计算TL的t时段的转移总功率。在TL转移时间约束(6)下，随机产生ta，并根据式(5)计算转移后时段的第k类可转移负荷量，然后求出转移后时段所有可转移负荷量之和。

步骤3计算电动汽车可交换的总功率。根据用户对电动汽车的行驶需求及其停放和离开的时间提前设定可交换功率，再由式(7)～式(9)计算单辆电动汽车的可交换功率，最后由式(10)计算电动汽车t时段的交换总功率。

步骤4获得电动汽车锂电池充放电功率Pc(t)。在式(13)的约束条件下随机产生Pc(t)，根据式(15)计算SOC(t)，检查是否满足式(15)～式(16)的当前荷电状态约束。

步骤5求解光伏微电网系统从配电网购电的功率Pg(t)。首先由公式(4)求得负荷侧在t时段的总功率需求，再由功率平衡等式约束(3)求取Pg(t)。

步骤6计算优化目标函数。由式(1)、式(11)、式(13)计算得到储能使用寿命的等效折损系数NT_sto；另外，由式(2)得到该周期内的光伏电网与配电网的交换电量。

图2 人工免疫算法主要步骤

4 算例分析

4.1 算例介绍

本算例所采用的相关数据来自作者所在单位的实际光伏微电网工程[9]。光伏电源系统额定功率为110 kW，电池储能的额定容量为50 kWh。有10台功率为10 kW的交换充电桩，电动汽车均为单位所有，员工出行可使用，用完归还到充电位进行充电。在微电网用电高峰期且是峰荷电价时多调用电动汽车对微电网进行调峰，在低谷电价时段对电动汽车充电，通常调节到00∶00以后。电动汽车锂电池容量均为20 kWh，而根据每辆电动汽车路途行驶的路程不同，其车载锂电池可输出功率也不相同。

假设算例中光伏微电网为某夏季典型日，电动汽车锂电池可充放电情况如图3所示，不包含储能的微电网系统的光伏出力和负荷情况如图4所示。其中，光伏电源全天总发电量为614 kWh；可转移负荷根据持续工作时间分为3类，分别为0.5 h、1 h及2 h，允许转移的时间范围是8∶00～22∶00。

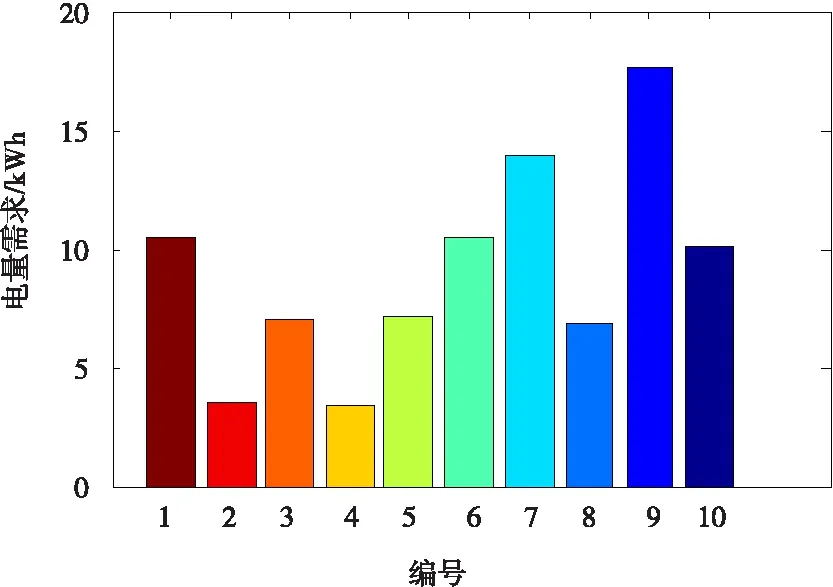
图3 电动汽车蓄电池可充放电情况

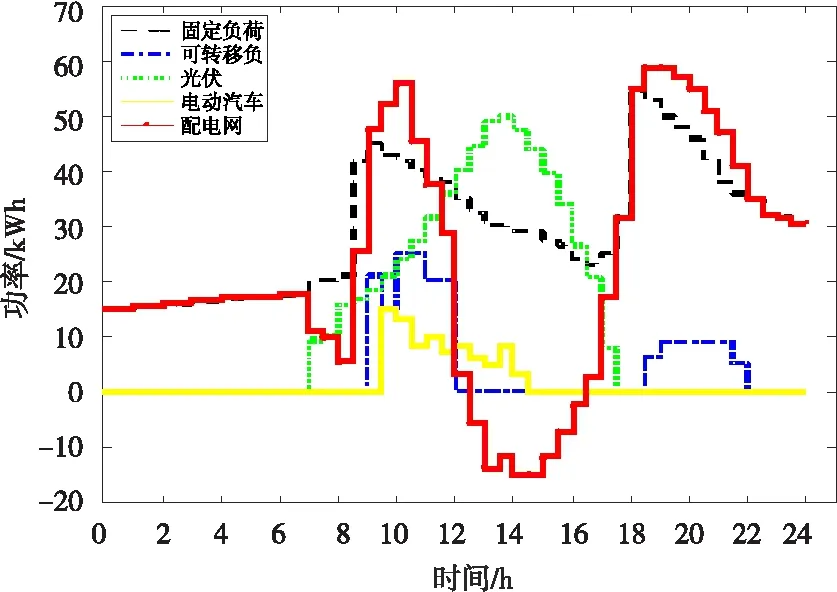
图4 不含储能的微电网光伏出力和负荷情况

由图3可知，在坐标轴下方的应为储能系统所存储的能量且此时由于储能电池容量限定，不得不减少光伏发电的量，即弃光减少发电，弃光后微电网系统的光伏出力和负荷情况如图5所示。因此，为使系统购电费用减小，此时购电费用为837.2元，必须要对系统运行进行优化。

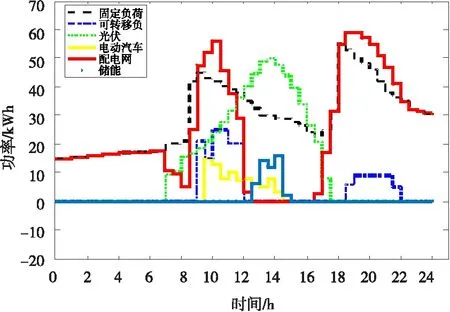
图5 弃光含储能的微电网光伏出力和负荷情况

微电网从配电网购电采用分时电价机制，将每天24 h的购电价格分成三个时段，见表1。

表1 不同时段购电价格

4.2 仿真分析

4.2.1 目标的优化结果分析

采用人工免疫算法对以上论述的目标函数进行求解，具体步骤描述如下：

初始化算法所有的参数值，包含抗体种群大小NP=70，免疫个体维数D=10，最大免疫代数G=500，变异概率为Pm=0.7，激励度系数alfa=1，belta=1，相似度阈值为detas=0.2，克隆个数Nc1=10，优化时间周期为24h，单位时间间隔为30 min。

为了分析需求侧响应对于光伏微电网运行的影响，定义了4种优化调度方案：(a)电动汽车放电和负荷转移同时参与优化；(b)电动汽车放电与无负荷转移优化；(c)电动汽车不放电但有负荷转移优化；(d)电动汽车不放电且无负荷转移优化。通过仿真，获得的蓄电池使用寿命折损系数和与配电网交换功率的Pareto最优解集如图6所示。

图6 4种方案的优化结果

由图6可知：(1)随着购电费用的增加，蓄电池折损系数逐渐降低，购电费用与蓄电池折损系数之间呈近似的反比例函数关系；(2)在光伏出力和其他配置不变的情况下，方案(a)与其他3种方案相比较，蓄电池折损系数和购电费用的Pareto最优解向坐标系左下方移动。上述现象表明，电动汽车放电或负荷转移参与优化调度有利于提高微电网的运行经济性，尤其当两者同时参与调度时，优化效果更为明显。

4.2.2 优化后各组件的功率变化

方案(a)电动汽车放电和负荷转移同时参与优化：购电费用为679.9305元，蓄电池使用寿命折损系数平均值为0.631；对应的光伏微电网中各部分的有功功率如图7所示。

图7 方案a各组件的有功功率

方案(b)电动汽车放电与无负荷转移优化：购电费用为702.8625元，蓄电池使用寿命折损系数平均值为0.667；对应的光伏微电网中各部分的有功功率如图8所示。

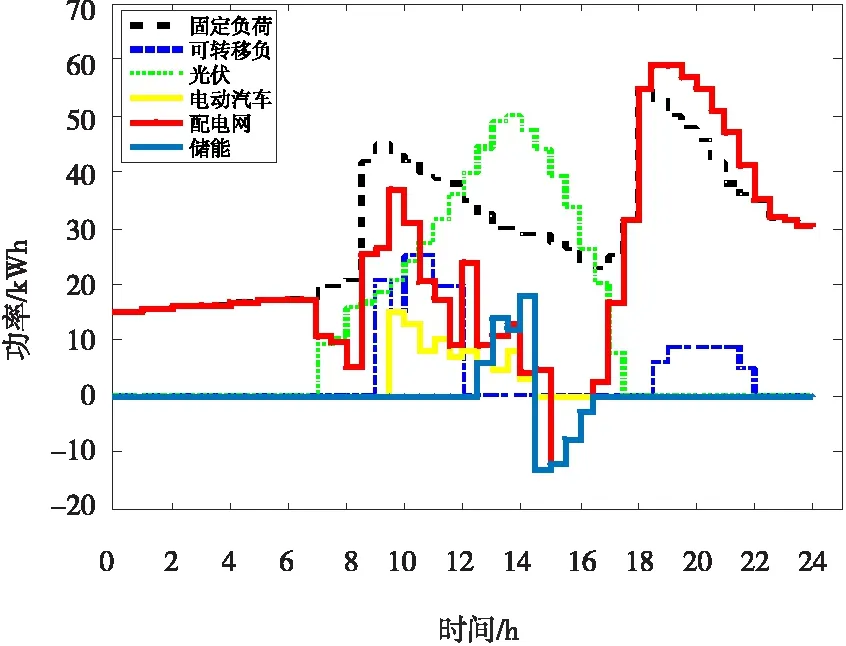
图8 方案b各组件的有功功率

方案(c)电动汽车不放电但有负荷转移优化：购电费用为756.2165元，蓄电池使用寿命折损系数平均值为0.526；对应的光伏微电网中各部分的有功功率如图9所示。

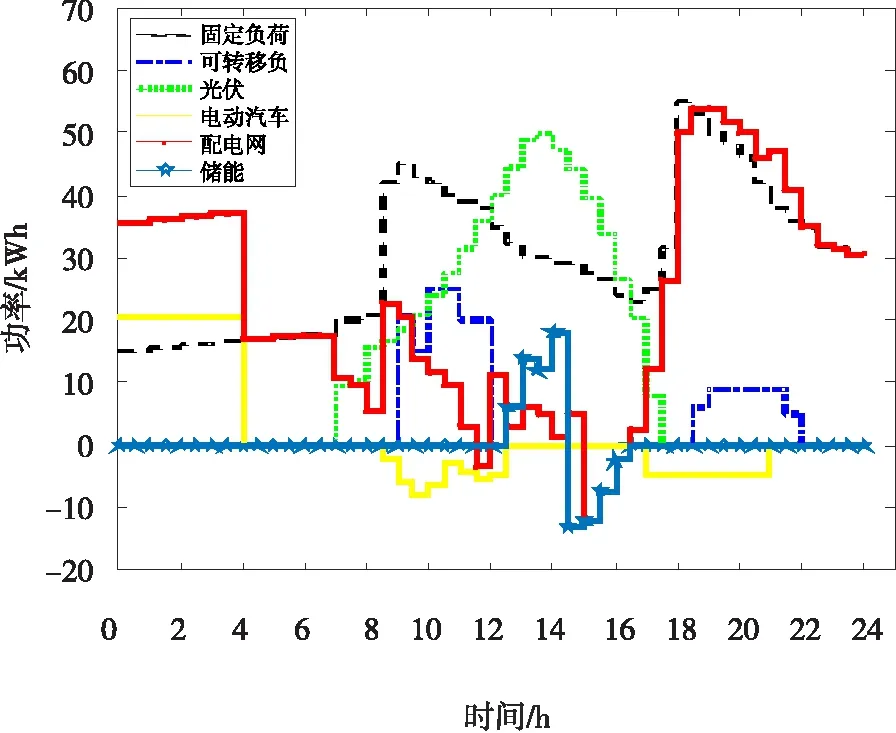
图9 方案c各组件的有功功率

方案(d)电动汽车不放电且无负荷转移优化：购电费用为779.1485元，蓄电池使用寿命折损系数平均值为0.667；对应的光伏微电网中各部分的有功功率如图10所示。

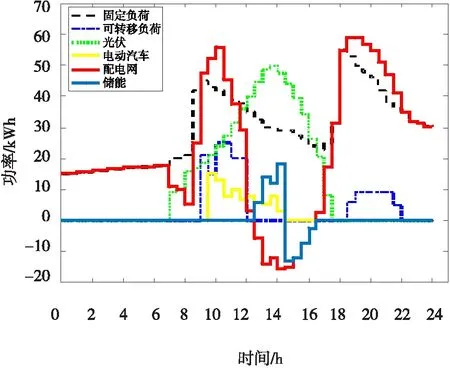
图10 方案d各组件的有功功率

由仿真分析可以看出，电动汽车参与的微电网优化调度方案提高了运行经济性，同时会给电动汽车锂电池带了折损，对微电网运行起到了一定的“削峰填谷”的作用，使得微电网运行更加稳定。

4.2.3 优化后系统运行情况说明

在Matlab平台仿真得到相应优化结果，并将本文提出的人工免疫算法导入微电网能量管理系统中，系统全局监控典型界面如图11所示，优化结果显示界面如图12所示。

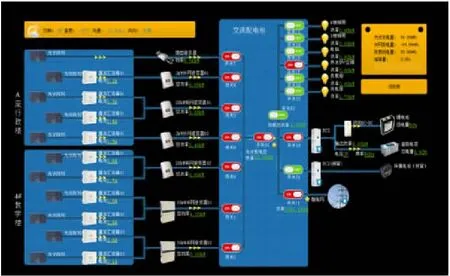
图11 系统全局监控典型界面

图12 系统优化结果显示界面

5 结 论

本文在简要分析光伏微电网结构基础上，重点将电动汽车锂电池作为微源参与微电网优化调度，在微电网系统运行的经济性和稳定性都有所提高，建立了以购电费用和电动汽车储能使用寿命为优化对象的模型，得出以下结论：

(1) 电动汽车充放电行为参与微电网优化运行，既可以提高微电网运行的经济效益，又可以在一定程度上起到“削峰填谷”的作用，保证微电网系统平稳运行。

(2) 提高了电动汽车的使用率，对加快推广V2G技术起到了一定的促进作用。

(3) 基于人工免疫算法的微电网侧需求响应优化调度对大电网平稳运行起到积极作用。

参考文献：

[1] 林茸.新能源电力系统中需求侧响应技术应用及发展[J].电子技术与软件工程,2017(19):249-249.

[2] 周伏秋,王娟.我国电力需求侧管理工作面临的形势及建议[J].电力需求侧管理,2015(2):1-4.

[3] ARABALI A,GHOFRANI M,ETEZADI-AMOLI M,et al.Genetic-algorithm-based optimization approach for energy management[J].IEEE Transactions on Power Delivery,2013,28(1):162-170.

[4] 刘晓飞,张千帆,崔淑梅.电动汽车V2G技术综述[J].电工技术学报,2012,27(2):121-127.

[5] 汪湘晋,赵波,吴红斌,等.并网型交直流混合微电网优化配置分析[J].电力系统自动化,2016,40(13):55-62.

[6] 吴雄,王秀丽,崔强.考虑需求侧管理的微网经济优化运行[J].西安交通大学学报,2013,47(6):90-96.

[7] 黄焘,马溪原,雷金勇,等.考虑分时电价和需求响应的家庭型用户侧微电网优化运行[J].南方电网技术,2015,9(4):47-53.

[8] 禹威威.智能光伏微网的能量优化管理方法研究[D].芜湖:安徽工程大学,2017.

[9] 路欣怡,刘念,陈征,等.电动汽车光伏充电站的多目标优化调度方法[J].电工技术学报,2014,29(8):46-56.

[10] 张帆,丁士明,陈汝昌,等.实时电力交易下的新能源电网能量管理策略[J].电力系统及其自动化学报,2015,27(6):86-90.

[11] 李保恩,李献伟,毋炳鑫.基于储能SOC状态的微电网能量优化调度策略研究[J].电力系统保护与控制,2017,45(11):108-114.

[12] 禹威威,刘世林,陈其工,等.考虑需求侧管理的光伏微电网多目标优化调度方法[J].太阳能学报,2017,38(11):2972-2981.

[13] LI N,CHEN L,LOW S H.Optimal demand response based on utility maximization in power networks[C]//Proceeding of 2011 IEEE Power and Energy Society General Meeting,San Diego,CA,USA,July 24-29,2011:1-8.

[14] 杨艳红,裴玮,邓卫,等.计及蓄电池储能寿命影响的微电网日前调度优化[J].电工技术学报,2015,30(22):172-180.

[15] 孙伟卿,王承民,曾平良,等.基于线性优化的电动汽车换电站最优充放电策略[J].电力系统自动化,2014,38(1):21-27.

[16] 丁明,王波,赵波,等.独立风光柴储微电网系统容量优化配置[J].电网技术,2013,37(3):575-581.

[17] 陶琼,李春来,穆云飞,等.考虑需求侧响应能力的孤立微网蓄电池储能系统容量概率规划方法[J].电力系统及其自动化学报,2017,29(1):37-44.

[18] 谢克明,郭红波,谢刚,等.人工免疫算法及其应用[J].计算机工程与应用,2005,41(20):77-80.

[19] 舒万能.人工免疫算法的优化及其关键问题研究[D].武汉:武汉大学,2013.

[20] 靳宗信.人工免疫算法及其在优化问题中的应用研究[D].重庆:西南大学,2007.