复合型连带Legendre方程边值问题解的相似结构
李顺初,赵超超,桂钦民
(1.西华大学 理学院 应用数学研究所,四川 成都 610039;2.北京东润科石油技术股份有限公司,北京 100029)
在解决石油等领域的实际问题时,常常会涉及到微分方程.因此,研究微分方程解的内在规律,对于其求解过程的简化起着至关重要的作用.近年来,就有相关研究报告对其作出了肯定回答[1-10].罗梅等[11]讨论了一般连带型Legendre微分方程边值问题解的相似结构,本文对复合型连带Legendre方程的边值问题进行了研究,获得了其解的相似结构.
本文研究如下边值问题:
(1)
其中:a,b,c,D,E,F,G,H,α,β,m1,m2,μ1,μ2为已知实常数,且D≠0,G2+H2≠0,-1 (2) 引理2关于二元函数 (3) 有: (4) (5) (6) 其中i=1代表左区(a 证明根据第一、第二类连带Legendre函数的微分性质[13]: (7) (8) 即证得式(4),同理可证式(5)、(6). 定理若边值问题(1)有唯一解,则其左区(a (9) 右区(c (10) 其中:Φ*(x)称为右区相似核函数, (11) Φ(x)称为左区相似核函数, (12) (13) (14) (15) (16) 联立式(13)~(16),求解出A1,A2,B1,B2,且根据边值问题(1)有唯一解得,对于待定系数A1,A2,B1,B2的线性方程组(13)~(16)的系数行列式Δ≠0,且 (17) 求解线性方程组(13)~(16),知 (18) (19) (20) (21) 将式(18)~(21)代入式(2)中,利用右、左相似核函数式(11)、(12)进行表达,即得到边值问题(1)的左、右区解分别为式(9)、(10). 推论1在边值问题(1)中,若右边界条件为y2(b)=0(即H=0,G≠0),则对应的右相似核函数为 (22) (23) 推论3边值问题(1)的解式(9)和其导数之间有如下性质: (24) 第六步:由式(10),组装边值问题(1)的右(c 求解下面的边值问题: (25) 第三步: 根据式(11),生成右相似核函数Φ*(x): 第四步: 根据式(12),生成左相似核函数Φ(x): 根据相似构造法的步骤可知,求解复合型连带Legendre 方程的边值问题时,首先通过连带Legendre方程的两个线性无关的解构造引解函数,其次由引解函数以及边界条件中的系数进行组装得到边值问题的解,可大大简化求解此类边值问题的运算步骤,达到事半功倍的效果,对解决石油等领域的问题有很大的帮助. 参考文献: [1] 李顺初,伊良忠,郑鹏社.微分方程定解问题解的相似结构[J].四川大学学报(自然科学版),2006(4):933-934. [2] 廖智健,李顺初.一种求解扩展Bessel方程的边值问题的新方法——相似结构法[J].中国科学技术大学学报,2013,43(12):975-979. [3] 李顺初,王俊超,许丽.复合油藏球向渗流问题的解的相似结构[J].数学的实践与认识,2014(3):122-127. [4] LI W,LI X P,LI S C,et al.The similar structure of solutions in fractal multilayer reservoir including a quadratic gradient term[J].Journal of Hydrodynamics,2012,24(3):332-338. [5] 李顺初,郑鹏社,张宇飞.复合油藏试井分析解的相似结构[J].数学的实践与认识,2008(3):23-28. [6] 徐昌学,李顺初,朱维兵.分形复合油藏试井分析解的相似结构[J].钻采工艺,2006(5):39-42. [7] 王强,李顺初,胡明.多层复合油藏渗流模型解的相似结构[J].重庆工商大学学报(自然科学版),2015(8):71-75,92. [8] 白丽霞,李顺初,桂东冬.复合型第二种Weber方程边值问题的新解法[J].中北大学学报(自然科学版),2014(6):633-637. [9] 范聪银,李顺初.双渗油藏渗流模型解的相似构造法[D].成都:西华大学,2014. [10] 李科,李顺初,董亚南.基于相似结构的合采油藏试井分析模型的求解[J].油气井测试,2013(2):7-9. [11] 罗梅,李顺初.连带Legendre微分方程边值问题解的相似结构[J].重庆工商大学学报(自然科学版),2015,11:34-37. [12] 刘式适,刘式达.特殊函数[M].北京:气象出版社,2002. [13] 王竹溪,郭敦仁.特殊函数概论[M].北京:北京大学出版社,2000.1 主要定理及其证明
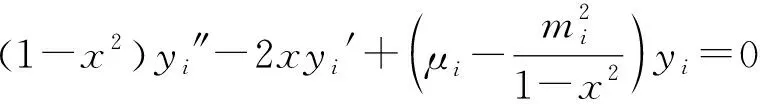
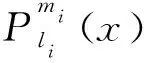
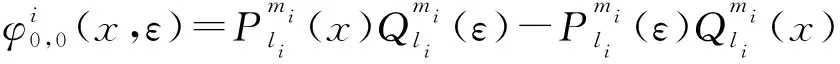
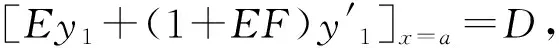
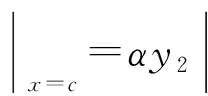
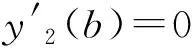
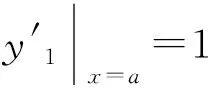
2 相似构造法步骤
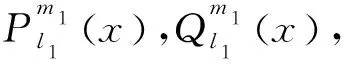
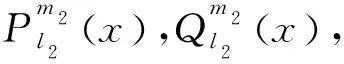

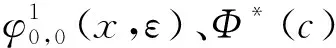
3 举例
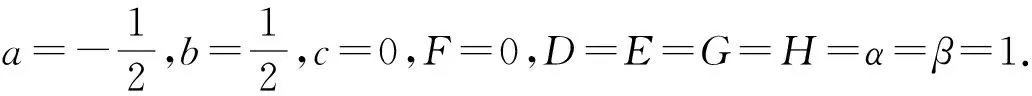
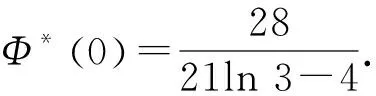
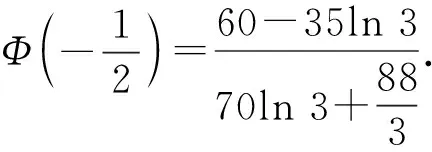
4 结语

