基于局部特征约束的TEM图像分割算法
魏本征 尹义龙
(1.山东中医药大学理工学院,济南,250355;2.山东中医药大学计算医学实验室,济南,250355;3.山东大学软件学院,济南,250100)
引 言
近年来,图像特征提取作为计算机视觉中最重要的一环,得到了极大的关注并取得一定进展[1,2]。局部图像信息特征是利用图像的局部结构关键点的相关信息来描述和表征图像的方式,它是图像语义描述和特征提取的一种方法。局部图像信息特征描述了图像中的区域信息,因各个局部区域间的形状、像素、颜色或纹理等方面的差异性,局部图像信息特征通常可体现出唯一描述性[3]。针对医学图像,主要是指具有显著性区别力的点集、边缘和感兴趣区域(包括:病灶区、组织器官结构等)以及局部区域图像强度、纹理等特征。利用局部图像信息特征描述图像可以将繁杂的图像描述问题转换为特征向量的度量问题,从而提高相关后继处理算法的速度和鲁棒性。但是基于局部特征的图像分割算法,在处理异质图像时易产生图像过分割问题。图像过分割是指分割区域过细,割裂了原有图像局部整体性的情况,即生成大量小的封闭区域,使目标物体′淹没′其中的分割情况。图像过分割的成因很多,主要是分割图像的局部特征对于分割算法过于敏感造成,这是一种非理想状态的图像分割结果,是各图像分割算法在实施分割过程中所极力避免的问题。然而,在某种规则或条件下产生的图像过分割结果因其在一定程度上反映了待分割图像的局部信息特性,过分割区域常具有良好的局部灰度、纹理等特性。因其这一局部特性,过分割图像逐渐引起了部分研究者的注意,并被逐步应用于医学图像分割中,特别是神经细胞透射电子显微镜(Transmission electron microscopy,TEM)图像的分割工作中。由于神经细胞本身及内部显微结构的复杂性,使得二维空间神经细胞TEM图像的自动分割充满挑战。图1为两幅典型的神经细胞TEM图像。在神经细胞TEM图像分割研究方面,文献[4]基于每个像素点属于细胞膜的概率的概率图,利用分水岭转换算法对细胞膜进行过分割,并利用随机森林进行区域合并,形成一种层次化的分割方法。文献[5]充分利用图像的几何特性和边界点的统计特征,提出一种基于概率图的分水岭合并树方法实现区域合并,取得了较好的图像分割效果。
计算机视觉领域中的一个新兴热点技术——超像素技术,也是以图像过分割为基础的。超像素作为一种新兴的图像分析方法,与以往的像素级描述信息方式不同,它能较好地描述局部像素区域(块)信息特征,并且对图像目标定位、操作等具有良好的局部特征不变性和鲁棒性。在一定分辨率下,TEM图像神经细胞细胞膜具有相应的宽度,且神经细胞内细胞器、细胞质等成分相似的显微结构,都使得相邻像素具有较高的相似性,如图2所示。TEM神经细胞图像具有典型局部聚簇性特征,因此可以考虑采用超像素技术予以处理。在前期研究中,本文作者也曾提出将超像素算法结合随机森林的方法应用于神经显微图像分割,并取得了良好的分割效果[6]。本文将超像素思想应用于神经细胞TEM图像分割中,充分利用图像局部信息,研究设计了一种基于局部空间信息的超像素医学图像分割方法——基于超像素的模糊C均值聚类医学图像分割算法(Superpixel-based fuzzy C-means clustering, SPFCM),并将该算法在神经细胞TEM图像集上进行性能测试。

图1 神经细胞TEM图像示例

Fig.2 TEM image of SLIC superpixels segmentation result
1 算法设计思想
1.1 超像素技术
超像素技术就是用某种算法将某些具有相似颜色、纹理等特征的相邻像素点聚集成一种新的可代替原有硬性分割的具有某种意义的区域网格[7]。图像的超像素一般通过设定图像分割数目或图像细化分割规则获得。超像素分割方法有很多,目前常用主要的方法有:Turbo pixel[8], Graph-Based[9], N-cuts[10], Quick Shift[11], Watershed[12], SLIC Superpixel[7]以及测地距离法[13]等。本文选取以聚类分割算法为基础的SLIC方法作为设计算法的基础,它以构造的颜色和空间相似度向量为依据,通过对像素点的聚类实现过分割,生成超像素粒度的数量虽不可控,但较为均匀[14]。
1.2 基于图模型的超像素图像结构表示
超像素图像在整体上会表现为内部像素同质化、形状不规则特性和粒度特征。因此,超像素图像的空间信息关系复杂,存在图像空间结构表示困难的问题。
考虑到图模型在空间结构表达方面的优势,为表达超像素图像空间结构信息,可借鉴图模型分割算法[15],对超像素图像采用基于无向图结构的整体性结构表达。其表示思路如下:由图模型结构理论,G=(V,E)表示一个无向图,顶点vi∈V,边(vi,vj)∈E连接相邻顶点对。每一条边(vi,vj)∈E有一个对应的权值bij((vi,vj)),bij是一个非负值,测量相邻顶点的相异程度。在基于图像像素分割情况下,顶点V是像素,边的权值是这条边相连的两个像素的相异度(如亮度差、颜色差等)[16]。基于此,在基于超像素图像的方法中,可以设定顶点V为超像素(像素块)集合。由此,一个分割S是对超像素集合V的一种划分的一个部分,每个分组C⊂S对应图中一个连通区域G′=(V,E′),E′⊂E。在一个分组中的超像素元素是相似的,在不同分组中的超像素元素特性是相异的,即在同一个分组中连接两个顶点(超像素点)的边的权值相对较小,连接在不同分组中的点的边权值较大。
1.3 Markov随机场邻域空间信息约束
在基于约束条件的图像分割方法中,贝叶斯方法因其在应用过程中的良好性能和更接近人类视觉机理的特性被广泛使用。其中,贝叶斯方法中的Markov随机场(Markov random field,MRF)、Gibbs随机场以及条件随机场中的邻域系统,可以很好地表征图像中像素点间的空间结构关系[17]。基于这个独特的优势特性,该类方法一直在机器视觉、生物特征识别等领域中被持续研究并广泛应用。也正是基于该特性,本文将MRF邻域空间信息表征技术引入基于图模型的超像素分割方法中,以弥补超像素分割方法中超像素点间邻域信息和约束不足的问题。
Markov随机场可以定义如下:假定待分割图像I是尺度大小为M×N的图像,则其在二维空间中可表示为I={I(i,j);1≤i≤M,1≤j≤N}。定义图像I的标记场X={xij,(i,j)∈S},其中S是图像I中全体像素点集合,xij为点(i,j)的标记,K是分割结果中的类别数,则X={xij,xij∈(1,2,…,K)}是对应于每个标记的实现。因此,在图像空间中,若将待分割图像I上的像素点(i,j)的邻域记为ηij,η={ηij,(i,j)∈S},只要其满足正概率性和Markov性,则该图像的标记场X就是一个Markov随机场。因此,可定义在邻域系η上的随机场X={Xij,(i,j)∈S} ,如果对于∀(i,j)∈S都有
P{Xij=xij|Xkl=xkl,(k,l)∈S,(k,l)≠(i,j)}=P{Xij=xij|Xkl=xkl,(k,l)∈ηij}
(1)
则称X是关于邻域系η的MRF。
2 SPFCM医学图像分割算法设计
将本文所提出的SPFCM算法应用于TEM图像细胞膜的分割,算法流程示意图如图3所示。
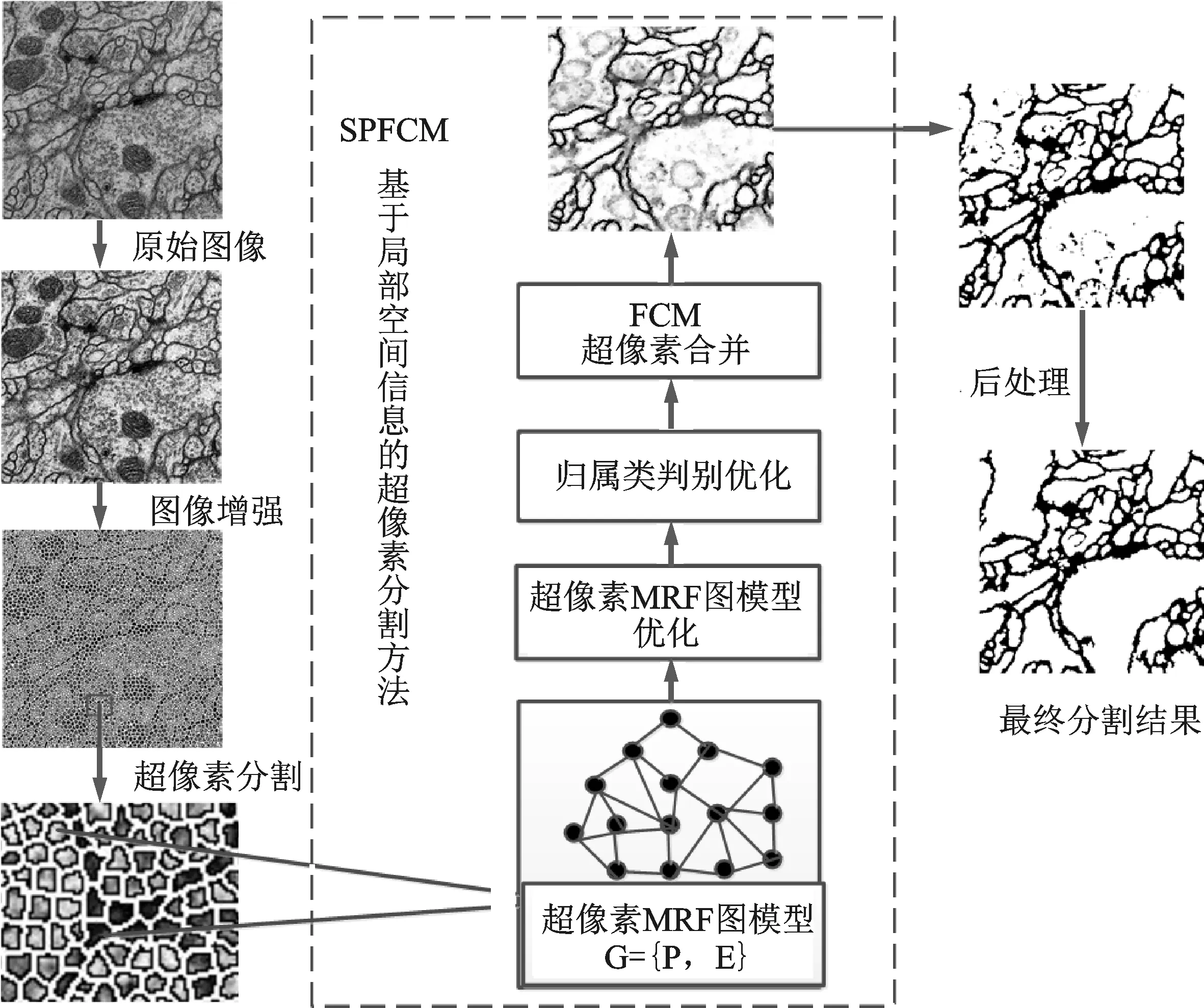
图3 SPFCM分割TEM图像细胞膜流程图Fig.3 Flow chart of SPFCM algorithm in TEM image segmentation
2.1 超像素图像的图模型表示
2.1.1 超像素形式化定义
定义1:若I是图像超像素集合,则图像I中第i个超像素Pi满足

(2)Pi内部PNi个像素相邻;
(3)|I(i,j)-I(i,k)|<τ。
式中:PN为图像I所含超像素个数;其中PNi是超像素Pi中的像素点个数;I(i,j)表示超像素Pi内像素点(i,j)的图像灰度值;τ是给定像素灰度阈值。
根据定义1可知,从图像I中提取的超像素Pi属性向量可表示为
Pi=(Ni,bi,Imax,Imin,μi,δi)
(2)
式中:bi是超像素Pi的周长,表示的是超像素Pi和周边相邻超像素的边界长度;Imax,Imin,μi和δi分别表示超像素Pi内像素灰度最大值、最小值、均值和方差,其相应计算式为
(3)
(4)
(5)
(6)
2.1.2 超像素集合形式化定义
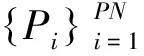
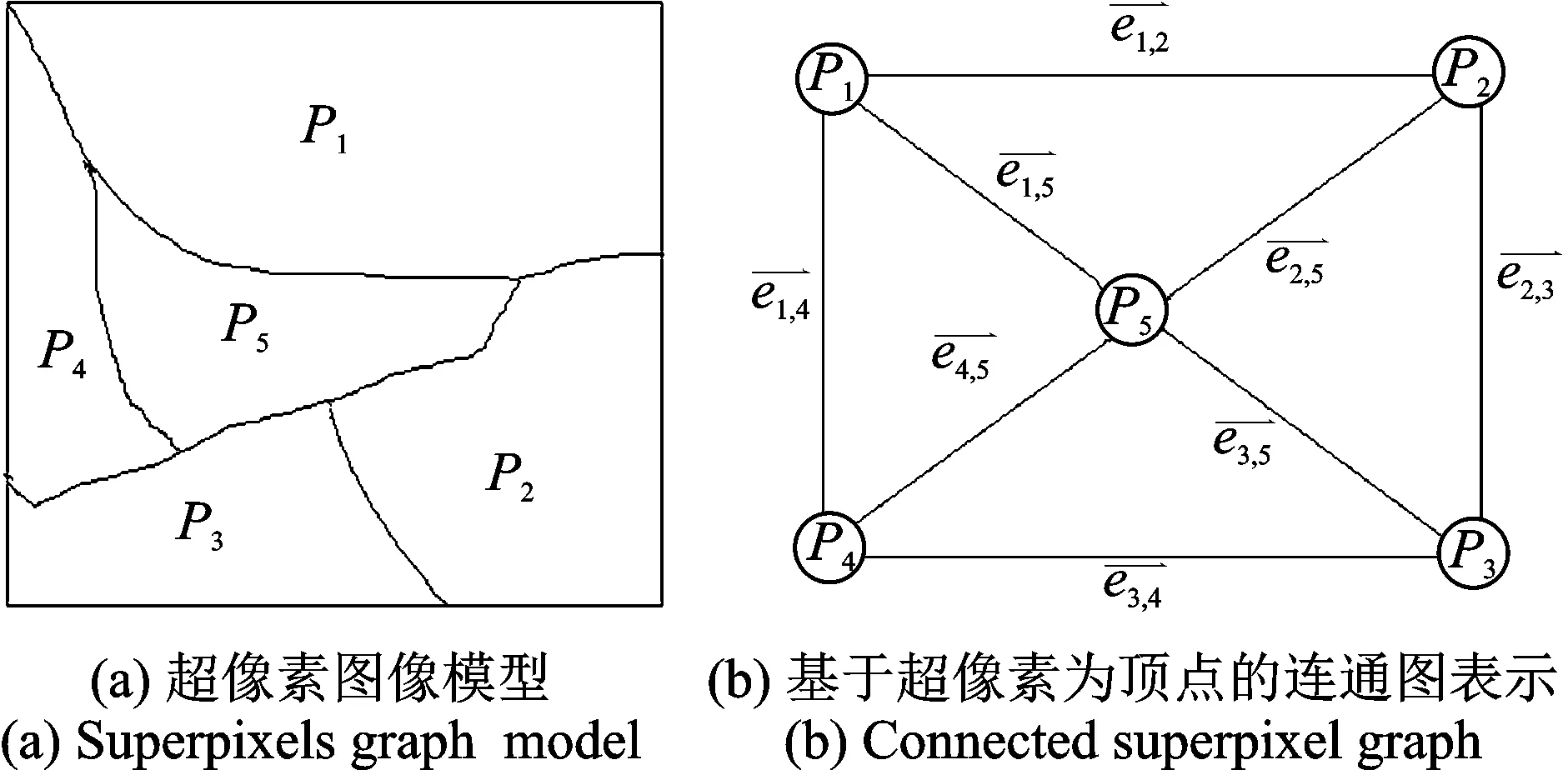
图4 超像素图模型表示示意图 Fig.4 Illustration of superpixels graph model
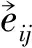
2.2 超像素MRF图模型
2.2.1 超像素图像MRF
令I表示观察图像(待分割图像),W表示分割图像(标记图像),G={P,E}是一个标记为划分集合ω所表示的基于超像素图像模型的图结构模型。假定观察图像I中的噪声为独立分布高斯白噪声,则由前述MRF理论,在贝叶斯图像分割框架下,分割图像可表示为
(7)
其中
P(W|I)∝P(I|W)P(W)
(8)
由于已经假定图像中的噪声是独立分布高斯白噪声,因此,如果超像素Pi属于k类超像素,则有
I(Pi)=μk+Sn
(9)
式中:I(Pi)是超像素Pi的图像灰度,表示超像素Pi内部像素图像灰度均值;μk是k类型超像素图像灰度均值,Sn是噪声。基于观测图像I,P(I|W)可表示为
(10)
式中:K是超像素的类目;Φk表示第k类超像素;I(Pi)为超像素Pi的图像强度,表示超像素Pi内部像素图像强度均值;μk和δk分别是第k类超像素的灰度均值和方差。由于同一超像素内的像素应该被分为同一类型,因此由式(7,10),基于用图像模型G={P,E}表示的图像I的超像素图像结构,可以得到P(I|W)基于观察图像I的表示
(11)
由于采用了超像素,对P(I|W)的计算量被大大简化。根据式(8),可知只需要计算出P(W),即可解决图像的分割问题,因其是一个先验概率,下面根据MRF理论来定义该先验概率的分布。
为构建基于超像素为像点的Markov随机场,图模型G中每个超像素的邻域系统可以定义为
ηP(P)={ηp(Pi)|Pi∈P}
(12)
其中,ηP(Pi)={Pj|∃eij∈E},1≤i≤PN。
令Λ={λ1,λ2,…,λK}表示分割图像中的类集合,L={l1,l2,…,lPN}是标记的随机变量组,其中li∈Λ表示第i类的标记,PN是图像I中超像素的个数。由于超像素内部像素点是统一的,因此分割图像I的标记就可以用图模型划分集合ω来描述,即:L=ω。
令Ω表示所有可能划分的集合,则Ω={ω=(ω1,ω2,…,ωPN)|ωi∈Λ,1≤i≤PN},则可定义一个Markov随机场,当且仅当满足下列两个条件:(1)P(L=ω)>0,∀ω∈Ω;(2)P(Li=ωi|Lj=ωj,Pi≠Pj)=P(Li=ωi|Lj=ωj,Pj∈ηP(Pi)),∀Pi∈P&∀ω∈Ω
2.2.2 超像素MRF图模型计算
根据MRF与Gibbs分布的等价性Hammersley-Clifford定理,P(L=ω)可改写为
(13)
其中T为一个温度常量,Z为归一化系数,其表达形式为
(14)
上式中,U(ω)是定义在所有划分集合ω上的能量函数,其计算形式为
(15)
且C={ci|ci={Pi}∪ηP(Pi),Pi∈P},其中C为子团,VC(ω)是子团的势能函数。
因此,可以基于MRF联合概率分布P(ω),将对MRF的概率分布的研究简化为对势函数VC(ω)的研究。因此对于图模型G中的每一个超像素,考虑到超像素间图像灰度关系,可以将其看作是一个子团。由此,可以得到子团势能的计算公式为
(16)
先验概率P(W)可定义为
(17)
可以看出,如何选择势能函数的形式和参数就成为需要解决的一个问题。
2.3 超像素MRF图模型优化
根据随机场理论,超像素图像分割过程实际上就是求式(8)中后验概率最大化的过程。因此根据MRF与Gibbs分布的等价性Hammersley-Clifford定理,为了获得较好的分割、分类效果,可以将超像素图像分割问题转化为优化问题,即将其转化为求后验能量函数的最小值问题。由于上述能量函数通常是非凸的,因而需要对该组合优化问题进行特别处理。根据MAP算法,由式(7),可得到
(18)
因此,可以根据式(11,17)得到P(W)目标函数的表达式为
(19)
其中,α=1/T是MRF模型的权重,它是图像分割准确度与平滑度之间的平衡因子。在目标函数表达式中,已经移除了常数项,聚类数K和权重α在优化之前需事先确定。使用模糊C-均值(FCM)聚类得到初始分割图像,初始化参数从最初的分割图像中依据超像素进行计算和估计,如均值μk和方差δk。然后再计算阈值T,T的值不应太大,否则本不属于同类的超像素将被错分为一类。在实际计算中可使用经验函数
(20)
最后对分割图像和参数同时进行优化,经超像素合并得到图像分割结果。
3 实验结果与分析
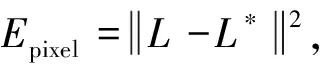
该算法性能指标评价由竞赛网站管理方提供:通过将TEM细胞膜图像分割结果提交至ISBI竞赛网站,网站系统将自动计算并返回上述3个评价指标的结果。
在测试集上,SPFCM测试的部分实验结果如图5所示,其中图5(a~c)分别为测试集中的待分割TEM图像,图5 (d~f)分别为经过后处理后的对应TEM图像分割结果。将SPFCM与当前具有代表性的先进方法进行了实验对比。对比方法选取专家手工分割、简单阈值法、Dense ETH方法[20](竞赛第1名)以及Burget方法[21](算法部分采用超像素技术)共4种方法,实验结果如表1所示。其中,对比实验结果并非本文重现,系直接引用自相应参考文献或竞赛网站,故对比试验所采用的特征及其分割方法等都与本文算法不同。由于各实验结果均是由竞赛网站系统按照统一评价指标所做出的评价和返回评价结果,因此各算法的实验结果具有可比性,能反映出算法的先进性。

图5 SPFCM算法分割TEM图像细胞膜部分结果示意图Fig.5 Partial segmentation result of TEM images by using SPFCM algorithm
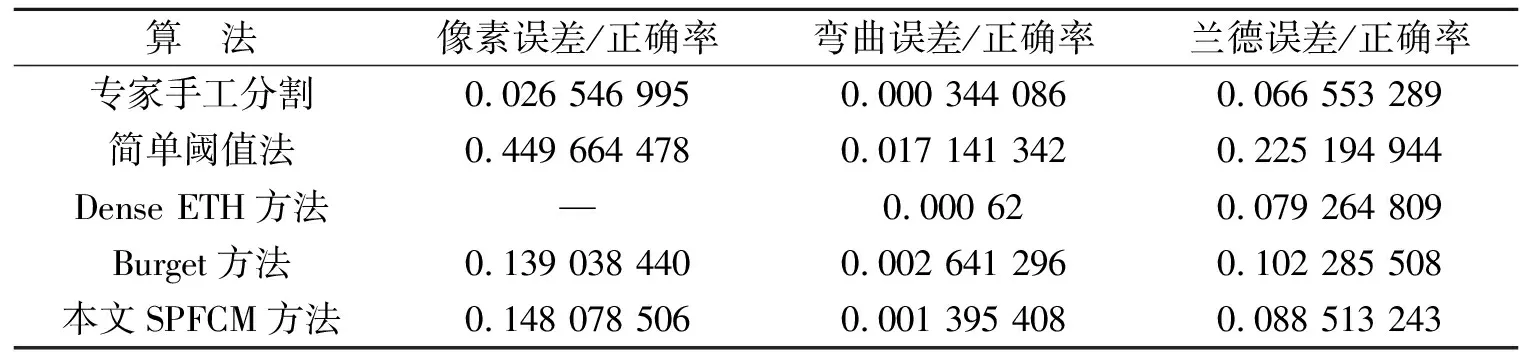
表1 各算法在ISBI竞赛数据集上的实验结果统计表
注:在文献[20]中,ETH方法没有提供像素误差。
从表1可以看出,SPFCM方法全面优于简单阈值法,且分割精度在弯曲误差和兰德误差指标相差一个数量级以上。SPFCM方法的弯曲误差和像素误差两个指标上相比Burget方法具有一定的优势。SPFCM方法的像素误差指标稍弱于Burget方法,与Dense ETH相比在弯曲误差指标较弱,兰德误差与其相差不大。这是由于:一方面,在特征提取阶段,ETH方法和Burget方法利用了参数优化并选取复杂的多级分类方案,并在最后分割中引入了相关机器学习的决策策略;另一方面,在初始超像素分割过程中,SPFCM方法的粗分割误差会对后继像素聚类分割产生影响。但是,SPFCM方法是基于超像素技术的,较为简单和直接。另外,由于采用了MRF超像素的邻域特征,本文提出的SPFCM方法在保持图像的拓扑结构、上下文信息以及图像的原始边界等方面具有较好的效果,因而其在弯曲误差和兰德误差两个指标上具有较好的算法性能,这也体现在SPFCM的兰德误差指标和专家手工分割的兰德误差相比差距不大,非常接近于专家手工分割结果。
SPFCM算法虽然部分评价结果比其他两种对比算法略差,但是实现了TEM图像的快速分割,算法的参数选择及图像特征无需进行训练,有效且适用范围较广,更便于实际应用。
4 结束语
本文基于超像素结合MRF空间邻域的方法,提出了一种基于局部特征约束的TEM图像分割算法,该方法是一种基于人工交互的新型医学图像分割算法,共分为4步:首先,利用SLIC算法实现TEM图像的超像素分割,获取超像素图像;然后采用图模型对难以表征的超像素空间结构进行表示,并构建相应图模型;在超像素图模型基础上,再利用Markov随机场的先验处理方式和良好局部图像邻域信息表达能力,引入MRF的邻域系统表示超像素图像中超像素局部空间信息;最后,采用邻域归属类判别优化算法对图像分割过程进行优化,合并同类超像素得到分割图像。研究结果表明,SPFCM是一种具有局部空间信息特性约束的超像素图模型分割算法,其算法性能优良,能有效地进行TEM图像的分割处理,并可获取较好的分割结果。
参考文献:
[1] James S D, Nicholas A. Medical image analysis: Progress over two decades and the challenges ahead[J].IEEE Transaction on Pattern Analysis and Machine Intelligence, 2000,22(l):85-104.
[2] 王仕民, 程柏良, 叶继华,等. 基于加权多尺度张量子空间的人脸图像特征提取方法[J]. 数据采集与处理, 2016, 31(4):791-798.
Wang Shimin, Cheng Bailiang, Ye Jihua, et al. Method for face image feature extraction based on weighted multi-scale tensor subspace[J].Journal of Data Acquisition and Processing, 2016, 31(4):791-798.
[3] Zhu Long (Leo), Chen Yuanhao, Yuille Alan. Recursive compositional models for vision: Description and review of recent work[J]. Journal of Mathematical Imaging and Vision, 2011, 41(12):122-146.
[4] Andres B, Köthe U, Helmstaedter M, et al. Segmentation of SBFSEM volume data of neural tissue by hierarchical classification[C]//Joint Pattern Recognition Symposium. [S.l.]:Springer Berlin Heidelberg, 2008: 142-152.
[5] Liu T, Jurrus E, Seyedhosseini M, et al. Watershed merge tree classification for electron microscopy image segmentation[J]. Proc IAPR Int Conf Pattern Recogn, 2012:133-137.
[6] Wang S, Cao G, Wei B, et al. Hierarchical level features based trainable segmentation for electron microscopy images[J]. Biomedical Engineering Online, 2012, 12(1):1-14.
[7] Radhakrishna Achanta, Appu Shaji, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Trans on Patten Analysis and Machine Intelligence, 2012,34(11): 2274-2281.
[8] Levinshtein A, Stere A, Kutulakos K N, et al. Turbo pixels: Fast superpixels using geometric flows[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2009, 31(12):2290-2297.
[9] Felzenszwalb P, Huttenlocher D. Efficient graph-based image segmentation[J]. International Journal of Computer Vision, 2004,59(2): 167-181.
[10] Shi J, Malik J. Normalized cuts and image segmentation[J]. IEEE Trans on Patten Analysis and Machine Intelligence, 2000, 22(8): 888-905.
[11] Vedaldi A, Soatto S. Quick shift and kernel methods for mode seeking[J].European Conference on Computer Vision, Lecture Notes in Computer Science , 2008, 53(5): 705-718.
[12] Vincent L, Soille P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations[J]. IEEE Trans on Patten Analysis and Machine Intelligence, 1991, 13(6): 583-598.
[13] 王爱齐,邱天爽. 基于测地距离的超像素生成方法[J].大连理工大学学报,2012, 52(4):610-614.
Wang Aiqi, Qiu Tianshuang. Superpixels construction method based on geodesic distance[J]. Journal of Dalian University of Technology, 2012, 52(4):610-614.
[14] Cong J, Wei B, Yin Y, et al. Performance evaluation of simple linear iterative clustering algorithm on medical image processing[J]. Biomedical Materials and Engineering, 2014, 24(6):3231-3238.
[15] Felzenszwalb P, Huttenlocher D. Efficient graph based image segmentation[J]. International Journal of Computer Vision ,2004,6(6):167-181.
[16] 袁淑娟,高秀芬.基于图像精确过分割的虚拟现实场景构建[J].计算机工程与设计,2009,30 (17):4044-4046.
Yuan Shujuan, Gao Xiufen. Virtual reality scene construction based on improved image over-segmentation[J].Computer Engineering and Design, 2009,30 (17):4044-4046.
[17] 刘思远,李晓峰,吴宏刚,等. FCM与马氏空间约束条件下的快速图像分割技术研究[J]. 计算机应用研究,2007, 24(8):71-74.
Liu Siyuan, Li Xiaofeng, Wu Honggang, et al. Research of fast image segmentation based on Markov spatial constraint and fuzzy C-means clustering[J].Application Research of Computers, 2007, 24(8):71-74.
[18] Yang F, Jiang T. Pixon-based image segmentation with Markov random fields[J]. IEEE Trans Image Process, 2003,12 (12):1552-1559.
[19] Jain V, Bollmann B, Richardson M, et al. Boundary learning by optimization with topological constraints[C]∥Proc of Computer Vision and Pattern Recognition (CVPR), IEEE Conference on. San Francisco, CA, USA: IEEE, 2010: 2488-2495.
[20] Laptev D, Vezhnevets A, Dwivedi S, et al. Anisotropic sstem image segmentation using dense correspondence across sections[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention.[S.l.]: Springer Berlin Heidelberg, 2012: 323-330.
[21] Burget R, Uher V, Masek J. Trainable segmentation based on local-level and segment-level feature extraction[C]//2012 IEEE International Symposium on Biomedical Imaging (ISBI).[S.l.]: IEEE, 2012.

