基于代价敏感主动学习算法的2型糖尿病诊断

许智彪

(上海交通大学电子信息与电气工程学院，上海 200240)

0 引 言

随着社会经济的发展和人民生活水平的提高，2型糖尿病已经成为严重威胁人类健康的重要疾病[1]。大量的研究[2-3]表明，对2型糖尿病提早进行干预是世界公认的能够降低心血管疾病发病率的有效措施。近年来，医疗数据挖掘在解决人们的健康问题上起到了重要的作用，也越来越受到广泛关注[4-7]。医疗数据挖掘不仅能够帮助医生进行诊断，使疾病在早期就能得到控制，使诊断和治疗更加便利和有效，它还能促进智能医疗系统的发展，从而在一定程度上节省人力劳动，减小区域间的医疗水平差异。

通过监督学习构建一个疾病诊断系统通常需要大量有标记数据来确保模型的质量，然而收集大量的有标记的医疗数据并不容易。首先，病人的诊断和治疗信息是高度敏感和隐私的，即使是用于科学研究，也只有极少的医院会愿意提供医疗数据。其次，医疗机构产生的数据很多是未标记的，医学诊断如果只使用那些标记的小部分样本，训练出的疾病诊断系统会缺乏泛化能力。如果人工地对这些数据进行标注不仅需要专业的医生，而且需要耗费大量的精力。因此，本文利用主动学习算法[8]，从未标注数据中有选择地选取那些最有利于提高诊断性能的样本进行标记，从而达到以尽可能少的标记成本获取尽可能高的诊断性能的目的。

糖尿病诊断可以看成是一个二分类问题，即患有糖尿病和不患糖尿病。传统的分类算法主要是以提升分类准确率为目标，认为不同的误分类有相同的代价或损失。然而，大部分医疗数据的类别是极其不平衡的，因为确诊的病人在人群中只占小部分。在糖尿病诊断中，不同的误分类会产生不同的代价，例如：把一个糖尿病患者误诊为正常人的代价要远远高于把一个正常人误诊为糖尿病患者的代价。前者会使得糖尿病患者有生命危险，而后者仅仅需要后续进一步检验。因此，在实际应用中需要考虑到不同的误分类代价，可使用代价敏感分类算法来解决。

本研究基于几种常用的分类模型，通过基于期望误差减小的代价敏感主动学习算法[9]，从无标注数据中选择对模型性能提升最有利的样本进行标记，来构建2型糖尿病诊断模型。本文将基于期望误差减小的代价敏感主动学习算法和其他主动学习算法进行对比，包括不确定性采样[10-11]、方差减小[12]和期望损失最优化[13]，根据模型在测试集上的误分类代价来评判各个主动学习算法的性能。

1 材料与方法

1.1 材料与数据

依据上海市长宁区卫生计生委提供的病人诊疗信息，共包含419868条糖尿病患者的诊疗信息作为正样本，5875664条非糖尿病患者的诊疗信息作为负样本。负样本和正样本的不平衡比率[14](imbalance ratio)是13.994。指标变量包括年龄、性别、白细胞计数、C反应蛋白(高敏)、总胆固醇、低密度胆固醇、高密度胆固醇、低密度脂蛋白、高密度脂蛋白、二小时血糖、甘油三酯、肌酐、空腹血糖、尿素氮、尿酸、尿微量白蛋白、全血粘度1、全血粘度5、全血粘度30、全血粘度50、全血粘度200、全血还原粘度：高切、全血还原粘度：低切、糖、糖化血红蛋白、糖化血清白蛋白、同型半胱氨酸、血红蛋白、平均红细胞血红蛋白含量、平均红细胞血红蛋白浓度、血小板、总胰岛素、空腹胰岛素、二小时胰岛素共34个与糖尿病有关的指标。表1列出了糖尿病患者和非糖尿病患者相应指标的均值和标准差(除性别外，性别是列出了男女数目)，经检验，34个指标的p值均<0.001，表明糖尿病和非糖尿病患者的相关影响因素之间差异均有统计学意义。

表1 糖尿病指标统计分析表

指标糖尿病非糖尿病指标糖尿病非糖尿病年龄70.30/11.4642.06/22.49全血粘度5(mPas)8.61/0.058.58/0.03性别(男/女)147898/2102951360311/4339790全血粘度30(mPas)5.46/0.015.43/0.01白细胞计数/(10^9/l)10.79/1.8417.05/1.15全血粘度50(mPas)4.51/0.024.56/0.02C反应蛋白/(高敏)(mg/dl)0.34/0.050.81/0.06全血粘度200(mPas)3.83/0.023.85/0.02总胆固醇/(mmol/l)4.85/0.335.05/0.19全血还原粘度:高切(mPas)5.53/0.185.48/0.07低密度胆固醇/(mmol/l)2.96/0.253.06/0.13全血还原粘度:低切(mPas)40.98/0.9541.00/0.38高密度胆固醇/(mmol/l)1.33/0.101.48/0.06糖1.26/0.051.08/0.02低密度脂蛋白/(mmol/l)2.84/0.122.92/0.09糖化血红蛋白(%)7.18/0.455.76/0.15高密度脂蛋白/(mmol/l)1.26/0.041.41/0.04糖化血清白蛋白6.90/0.245.16/0.11二小时血糖/(mmol/l)11.31/0.537.15/0.25同型半胱氨酸(umol/l)15.28/0.9511.12/0.74甘油三酯/(mmol/l)1.81/0.381.65/0.15血红蛋白(g/l)128.34/6.82127.45/7.47肌酐/(umol/l)81.82/22.39140.65/197.13平均红细胞血红蛋白含量(pg)30.28/0.7929.70/0.66空腹血糖/(mmol/l)7.72/0.715.49/0.24平均红细胞血红蛋白浓度(g/l)330.48/2.35331.72/2.31尿素氮/(mmol/l)8.12/2.685.16/1.15血小板(10^9/l)197.14/28.00214.80/27.30尿酸/(umol/l)327.28/33.84346.89/90.90总胰岛素(uIU/ml)24.41/9.3515.94/2.90尿微量白蛋白/(mg/l)72.05/19.8566.11/15.20空腹胰岛素(pmol/l)154.60/24.6764.56/7.08全血粘度/(1 mPas)19.16/0.1119.04/0.07二小时胰岛素(pmol/l)424.03/28.69401.13/18.24

1.2 逻辑回归模型

其中，θ是模型的参数，为了简化，把偏差项包含在了x和θ里。进一步地，后验概率可以被定义为：

P(y|x;θ)=p(x;θ)y(1-p(x;θ))(1-y)

逻辑回归模型通常通过最大化逻辑似然函数来训练，逻辑似然函数可以定义为：

根据Newton-Raphson[15]方法，逻辑似然函数的最大值可以通过下面的模型参数更新法则取得：

θ←θ-H-1Lθ

其中，H是Hessian矩阵。给定训练集D，在主动学习过程中，每次新添加一个样本(x+,y+)，模型需要在新扩充的数据集D+上重新训练，为了提升效率，有效的模型更新方法[9]为：

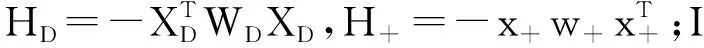
1.3 支持向量机模型

支持向量机模型在实际的二分类问题中表现了良好的学习和泛化能力，在解决小样本、高维度、非线性识别任务中展现了一定的优势，已被广泛应用于图像处理、疾病诊断等领域。建立支持向量机模型相当于解决下面的最优化问题[9]：

ξi≥0, i=1,2,…,n

其中,w和b是支持向量机分隔超平面的参数，ξi为函数间隔满足一定的限制所添加的补偿，φ(xi)是从输入空间到某个特征空间的映射，即先将数据映射到某个特征空间，然后再在特征空间内用线性学习器分类。支持向量机的决策函数可以定义为：

f(x) =sign(wTφ(x)+b)

其中，αi是拉格朗日乘子。

1.4 人工神经网络模型

人工神经网络模型是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一[16]。人工神经网络模型是由一个多层神经元结构组成，每一层神经元拥有输入(它的输入是前一层神经元的输出)和输出，每一层由N个网络神经元组成，分别与前一层的神经元相连，相连接的权重则是需要学习的模型参数。通常人工神经网络的结构包括输入层(Input Layer)、隐含层(Hide Layer)和输出层(Output Layer)。

1.5 基于期望误差减小的代价敏感主动学习算法

假设在训练集D上训练的模型记为fD(·)，在D+上训练得到的模型记为fD+(·)。在本文中，选用基于期望误差减小[17](Expected Error Reduction)的代价敏感主动学习方法，每次选择标记的样本是那些标记后能够使模型的期望误差最小的样本x*：

其中，U是无标记的样本集合，K是所有类别的数量，在本研究中K=2。P(y+=yk|x+)可以通过现有的模型fD(·)来计算，EL(x,fD+(x))是样本x的期望损失。

对于代价敏感分类问题，误分类的代价通常可以用一个代价矩阵C来表示[18]，其中元素C(i,j)表示把一个标签为j类的样本误分类为i类的代价。特别地，二分类的代价矩阵如表2所示，其中C(0,0)=C(1,1)=0，这是因为预测正确的代价通常为0。

表2 二分类任务的代价矩阵

预测样本实际样本实际为负样本实际为正样本预测为负样本C(0,0)C(0,1)预测为正样本C(1,0)C(1,1)

在代价敏感分类任务中，模型fD+(·)会把样本x的标签预测为使得它的期望损失最小的类别：

其中，P(y=j|x)可以通过模型fD+(·)来计算。因此，在代价敏感二分类任务中，样本x的期望损失被定义为[9]：

=min {P(y=0|x)C(1,0),P(y=1|x)C(0,1)}

2 实验结果

2.1 数据预处理

在所有的糖尿病指标中，并不是所有的样本都检测了这些指标，缺失的部分用相应指标的平均值来进行填充。然后，选用min-max[19]方法将每个特征都归一化到[0,1]范围内：

2.2 实验设置

将整个数据集随机划分为互不重合的3个部分[19-20]：初始训练集、未标记的数据集和测试集。初始训练集用来训练初始的基础模型，然后依据相应的主动学习算法从未标记数据集中选取样本，标记后放入训练集中，更新模型的参数，并在测试集上进行性能测试。本文选取整个数据集的0.001%作为初始训练集，20%作为测试集，剩余的作为未标记的数据集。主动学习过程共迭代10次，每次迭代选取所有样本的0.001%进行标记。为了避免结果的随机性，每个实验重复10次，每次实验重新随机划分数据集，最终取平均结果。

在代价敏感分类任务中，对最后的性能评估有影响的是不同误分类代价的比率[21-22]，即C(0,1)/C(1,0)，而不是C(0,1)和C(1,0)本身。在本研究中，使用2种代价比率。自适应的代价比率，即代价的比率等于类别的不平衡比率：C(0,1)/C(1,0)=13.994；固定代价比率：C(0,1)/C(1,0)=20。

为了证明期望损失减小(EER)这种主动学习方法在构建糖尿病诊断模型中的有效性，本文将它与下列主动学习算法进行对比：

1)随机选取(Random， RAND)。不采用任何主动学习算法，而是随机选取样本进行标记，常被用作比较的基准线。

2)不确定性采样[10-11](Uncertainty Sampling， US)。选取当前模型最不确定的样本进行标记。

3)方差减小[12](Variance Reduction， VR)。选取使得模型的输出方差最小的样本来间接地最小化模型的泛化误差。

4)期望损失最优化[13](Expected Loss Optimization， ELO)。选取在当前模型下期望损失最大的样本。

2.3 实验结果

本文用Matlab软件，分别以逻辑回归模型、支持向量机模型和人工神经网络模型为基础建立糖尿病诊断模型，并在预处理后的数据集上进行实验。5种主动学习方法在糖尿病诊断任务中的表现如图1～图6所示，横轴表示主动学习过程中的迭代次数，纵轴表示在测试集上的平均误分类代价。

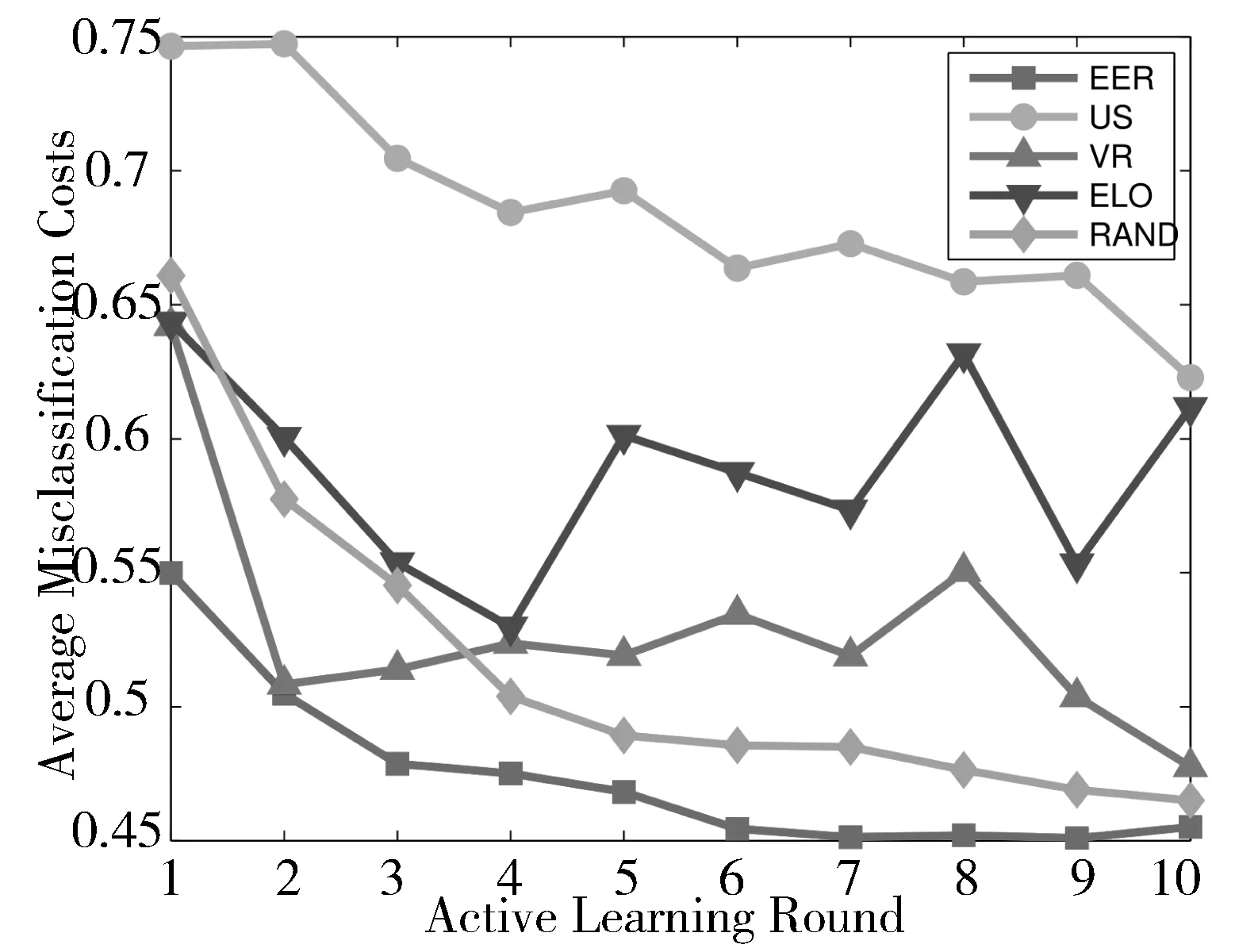
图1 基于逻辑回归模型在自适应比率下5种主动学习算法的性能比较

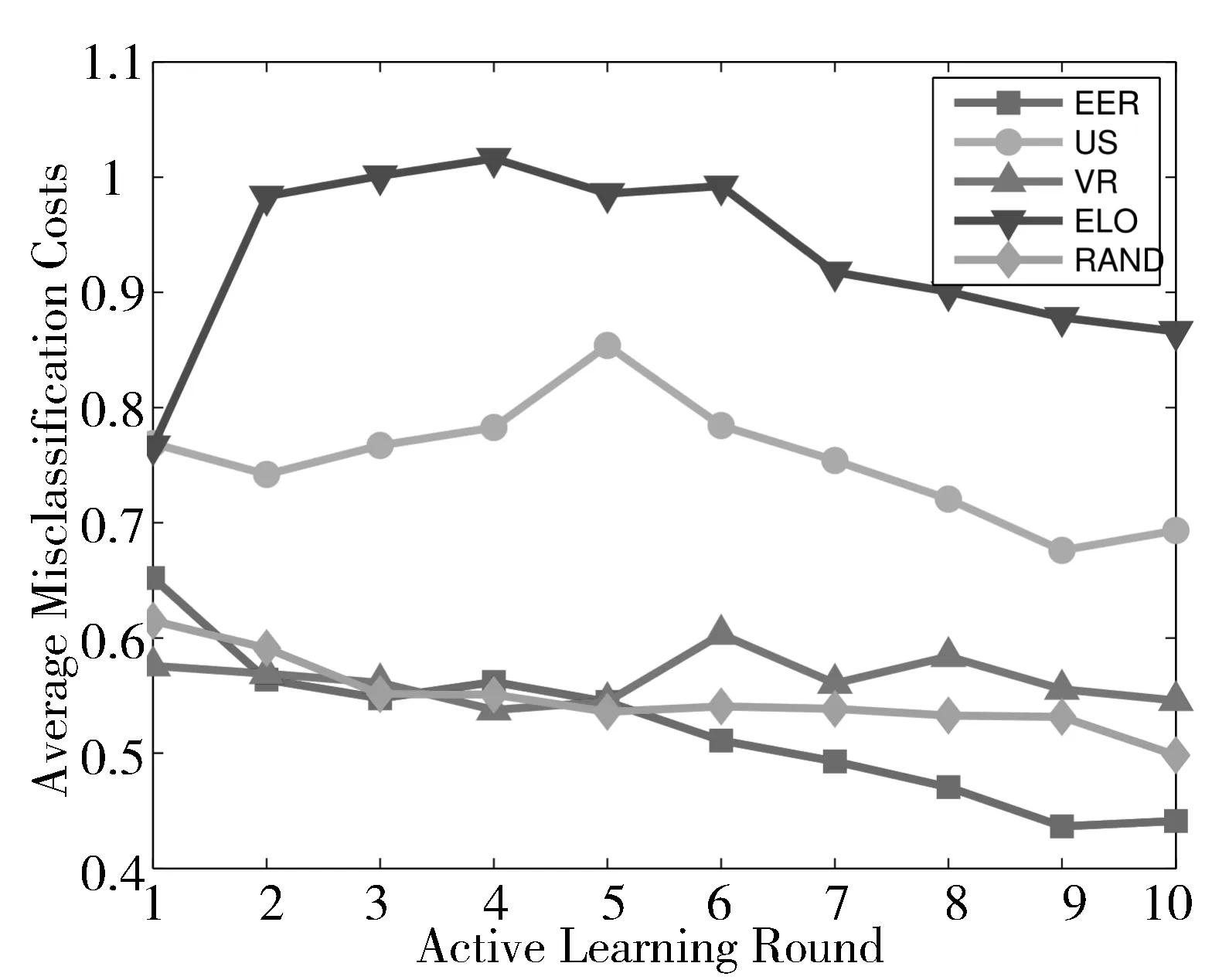
图2 基于逻辑回归模型在固定比率下5种主动学习算法的性能比较

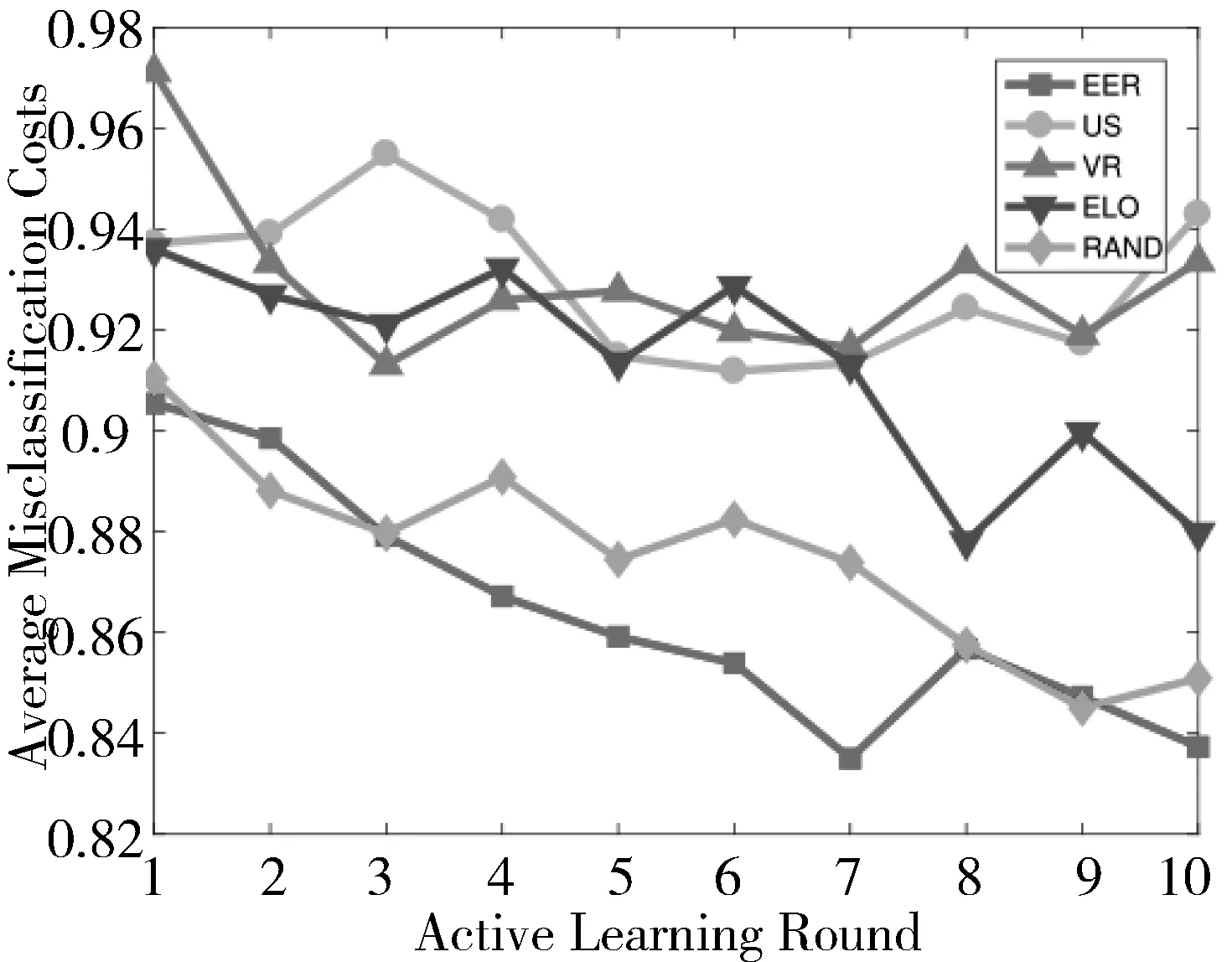
图3 基于支持向量机模型在自适应比率下5种主动学习算法的性能比较

图4 基于支持向量机模型在固定比率下5种主动学习算法的性能比较

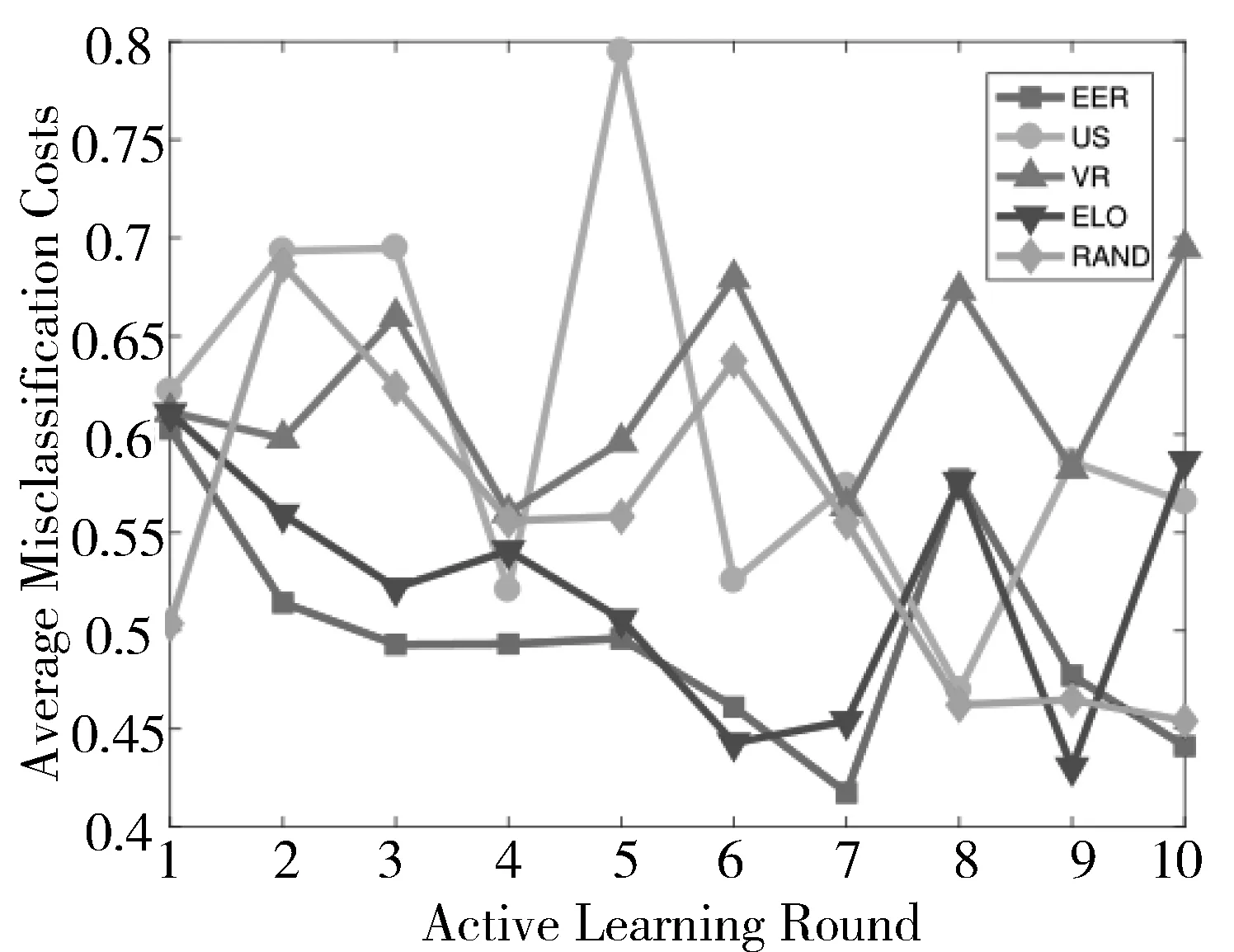
图5 基于神经网络模型在自适应比率下5种主动学习算法的性能比较

图6 基于神经网络模型在固定比率下5种主动学习算法的性能比较

从图1～图6可以看出，随着主动学习次数的增加，在测试集上的误分类代价也呈下降趋势，说明模型的性能随着训练数据的增加而提升。在整个主动学习过程中，基于期望误差减小的代价敏感主动学习算法在这5种方法中表现最优。这是因为这种主动学习算法选取那些使得模型的期望误分类代价最小的样本，它考虑到了不同的误分类带来的不同代价。因此，在代价敏感分类任务中，期望损失减小选择的样本能够更有效地提升模型的性能。此外，可以观察到期望损失减小使得模型在测试集上的误分类代价收敛得最快，即标记较少的样本就能达到最低的误分类代价。基于期望损失减小的主动学习算法在逻辑回归模型、支持向量机模型和人工神经网络模型上都表现最优，表明其稳定性和普适性。

为了更好地进行比较，本文画出了主动学习停止点(第10次迭代)处的误分类代价的分布情况，如图7～图12的箱形图所示，横坐标代表各个主动学习算法，纵坐标代表在测试集上的误分类代价。图中最上方的短横线表示分布的最大值，第二条线表示四分之三分位数，中间的线表示中位数，第四条线表示四分之一分位数，最下面的短横线表示分布的最小值。从图7～图12可以看出，期望误差减小的表现优于其他主动学习算法。

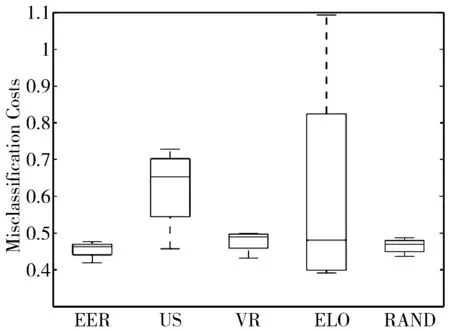
图7 基于逻辑回归模型在自适应比率下主动学习停止点的误分类代价的分布

图8 基于逻辑回归模型在固定比率下主动学习停止点的误分类代价的分布

图9 基于支持向量机模型在自适应比率下主动学习停止点的误分类代价的分布

图10 基于支持向量机模型在固定比率下主动学习停止点的误分类代价的分布

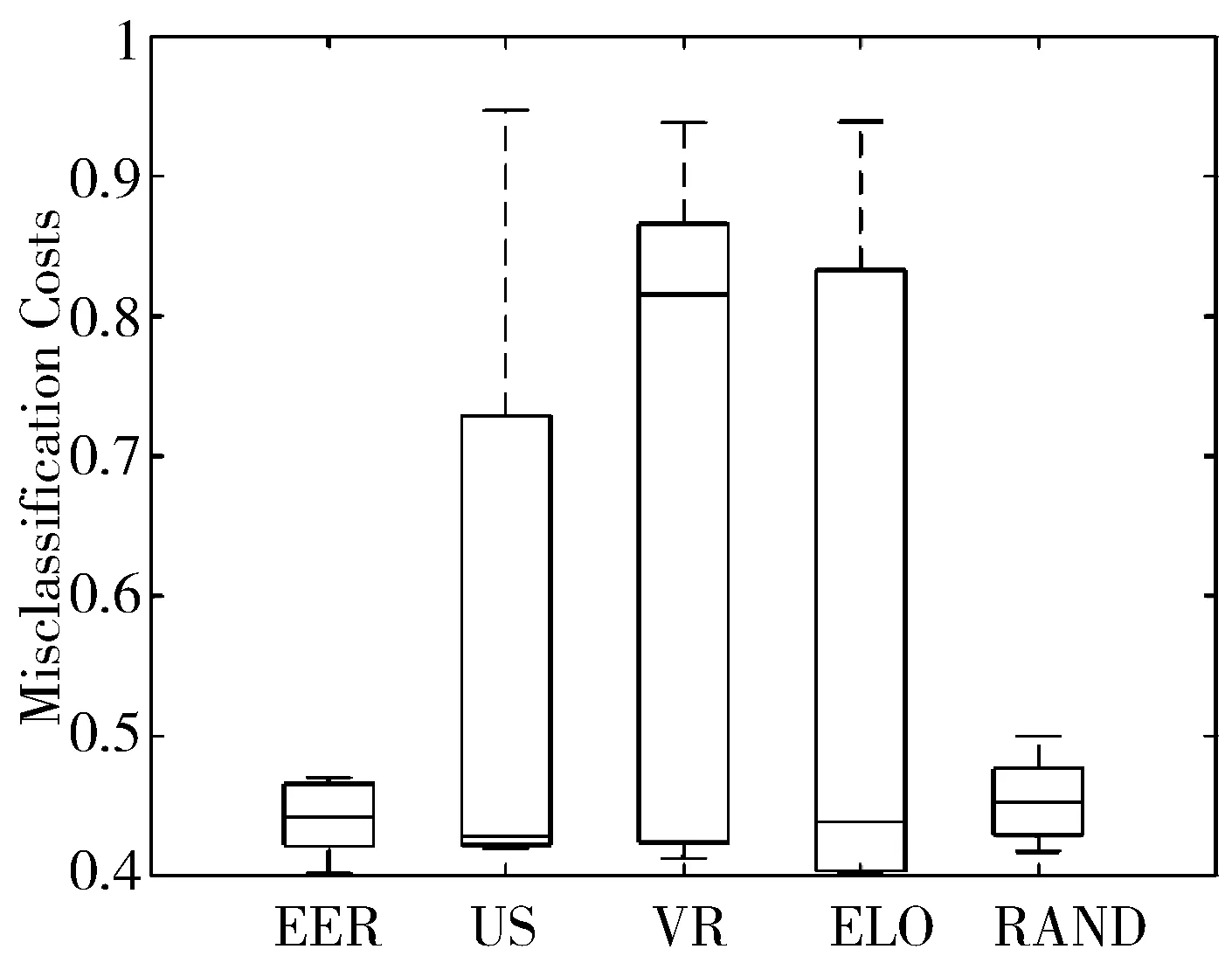
图11 基于神经网络模型在自适应比率下主动学习停止点的误分类代价的分布

图12 基于神经网络模型在固定比率下主动学习停止点的误分类代价的分布

在预测模型的评价中，除了误分类代价之外，灵敏度(Sensitivity)和特异度(Specificity)也是其中较为重要的指标，较高的灵敏度、特异度和AUC表示较好的预测性能。以逻辑回归模型在自适应误分类代价比率下为例，画出了不同的主动学习算法迭代10次后模型的ROC曲线，如图13所示。从图13中可以看出在同样的特异度下，EER得到的模型的灵敏度要比其他主动学习算法高，且EER的AUC最高，表明在代价敏感分类问题中EER主动学习算法优于US、VR、ELO等主动学习算法。

图13 ROC曲线分析

此外，本文对逻辑回归模型的参数进行了分析(见表3)，根据逻辑回归模型的参数选出了对2型糖尿病诊断最为重要的10个检测指标，并列出了相对应的统计检验p值，这10个指标分别是年龄、糖化血红蛋白、空腹血糖、C反应蛋白(高敏)、平均红细胞血红蛋白含量、二小时血糖、尿素氮、甘油三酯、空腹血糖和血红蛋白。p<0.001表明所列的指标参数均具有统计学意义。

表3 2型糖尿病指标分析

指标年龄糖化血红蛋白空腹血糖C反应蛋白(高敏)平均红细胞血红蛋白含量参数676.211622.233520.7478-14.6567-8.4764P值<0.001<0.001<0.001<0.001<0.001指标二小时血糖尿素氮甘油三酯空腹血糖血红蛋白参数6.95406.29495.39014.93004.8558P值<0.001<0.001<0.001<0.001<0.001

3 结束语

本文实验结果表明可以利用主动学习算法有选择地标记样本，用尽可能少的标记成本获得尽可能好的模型，从而解决医疗数据中标记样本较少的问题。先前的研究大多基于提高预测准确率或减小0-1损失，而没有考虑到不同的误分类带来的不同代价。基于代价敏感分类模型建立的糖尿病诊断模型，可以考虑到不同的误分类带来的不同代价，从而更好地帮助医生做出代价最小的诊断。

通过比较不同的主动学习算法可以发现，期望误差减小这一主动学习方法在糖尿病的诊断中表现最优。在标记的样本数一样的情况下，由它选择标记的样本能够使得模型在测试集上的误分类代价最小。在测试集上的误分类代价一样的情况下，它需要选择标记的样本数最少。

需要注意的是本文的实验是基于上海市长宁区的数据，而糖尿病的患病人群分布比较广泛，所以本文模型的泛化性能还需更多的数据进行验证，才能证明模型可以推广到更多人群。

参考文献：

[1] Nathan D M, Buse J B, Davidson M B, et al. Medical management of hyperglycemia in type 2 diabetes: A consensus algorithm for the initiation and adjustment of therapy[J]. Clinical Diabetes, 2009,27(1):4-16.

[2] Whiting D R, Guariguata L, Weil C, et al. IDF diabetes atlas: Global estimates of the prevalence of diabetes for 2011 and 2030[J]. Diabetes Research and Clinical Practice, 2011,94(3):311-321.

[3] Norris S L, Kansagara D, Bougatsos C, et al. Screening adults for type 2 diabetes: A review of the evidence for the U.S. Preventive Services Task Force[J]. Annals of Internal Medicine, 2008,148(11):855-868.

[4] Detrano R, Janosi A, Steinbrunn W, et al. International application of a new probability algorithm for the diagnosis of coronary artery disease[J]. The American Journal of Cardiology, 1989,64(5):304-310.

[5] Gamboa A L G, Mendoza M G, Orozco R E I, et al. Hybrid fuzzy-SV clustering for heart disease identification[C]// IEEE International Conference on Computational Intelligence for Modeling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. 2006:121.

[6] Kahramanli H, Allahverdi N. Extracting rules for classification problems: AIS based approach[J]. Expert Systems with Applications, 2009,36(7):10494-10502.

[7] Cascio D, Fauci F, Magro R, et al. Mammogram segmentation by contour searching and mass lesions classification with neural network[J]. IEEE Transactions on Nuclear Science, 2006,53(5):2827-2833.

[8] Settles B. Active Learning Literature Survey[R]. University of Wisconsin-Madison, Computer Science Report 1648. 2009.

[9] Zhang Yexun, Wang Yanfeng, Cai Wenbin, et al. From theory to practice: Efficient active cost-sensitive classification with expected error reduction[C]// Proceedings of the 2017 SIAM International Conference on Data Mining. Society for Industrial and Applied Mathematics. 2017:153-161.

[10] Liu A, Jun G, Ghosh J. A self-training approach to cost sensitive uncertainty sampling[J]. Machine Learning, 2009,76(2-3):257-270.

[11] Lewis D D, Gale W A. A sequential algorithm for training text classifiers[C]// Proceedings of the 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. 1994:3-12.

[12] Schein A I, Ungar L H. Active learning for logistic regression: An evaluation[J]. Machine Learning, 2007,68(3):235-265.

[13] Long Bo, Chapelle O, Zhang Ya, et al. Active learning for ranking through expected loss optimization[J]. IEEE Transactions on Knowledge and Data Engineering, 2015,27(5):1180-1191.

[14] Lopez V, Fernandez A, Moreno-Torres J G, et al. Analysis of preprocessing vs. cost-sensitive learning for imbalanced classification. Open problems on intrinsic data characteristics[J]. Expert Systems with Applications, 2012,39(7):6585-6608.

[15] Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference and Prediction[M]. 2nd ed. Springer, 2009.

[16] Baxt W G. Use of an artificial neural network for the diagnosis of myocardial infarction[J]. Annals of Internal Medicine, 1991,115(11):843-848.

[17] Roy N, Mccallum A. Toward optimal active learning through sampling estimation of error reduction[C]// Proceedings of the 8th International Conference on Machine Learning. 2001:441-448.

[18] Elkan C. The foundations of cost-sensitive learning[C]// International Joint Conference on Artificial Intelligence, 2001. 2001:973-978.

[19] Cai Wenbin, Zhang Ya, Zhou Siyuan, et al. Active learning for support vector machines with maximum model change[C]// Joint European Conference on Machine Learning and Knowledge Discovery in Databases. 2014:211-226.

[20] Zhou Siyuan, Zhang Ya. Active learning for cost-sensitive classification using logistic regression model[C]// IEEE International Conference on Big Data Analysis. 2016:1-4.

[21] Domingos P. Metacost: A general method for making classifiers cost-sensitive[C]// Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 1999:155-164.

[22] Wang Tao, Qin Zhenxing, Zhang Shicao, et al. Cost-sensitive classification with inadequate labeled data[J]. Information Systems, 2012,37(5):508-516.