DoFFT:一种基于分布式数据库的快速傅里叶变换方法
季 朋,李 晖,陈 梅,戴震宇
(1.贵州大学计算机科学与技术学院,贵州 贵阳 550025;2.贵州省先进计算与医疗信息服务工程实验室,贵州 贵阳 550025)
0 引 言
快速傅里叶变换(FFT)[1]算法是数字信号处理中的核心算法,在频谱分析、数字通信、图像处理中有着重要的应用。快速傅里叶变换在天文学方面也有大量应用,一个典型的应用场景是对脉冲星信号进行相干消色散处理[2]。脉冲星辐射的电磁波在传播过程中,由于受到星际介质的干扰,不同频率的电磁波经过星际介质后,会引起观测到的脉冲星轮廓展宽,所以需要进行消色散处理。消色散处理通常使用相干消色散算法。相干消色散算法的基本原理[3]是将基带脉冲星数字信号进行快速傅里叶变换,然后将频域上各频点的信号乘以星际介质函数CHIRP即频率的响应函数,最终逆傅里叶变换到时域,从而实现将不同频率成分的脉冲星型号对齐到某一频点。傅里叶变换的快慢直接决定相关消色散的处理效率。
为了满足海量信号数据的存储与分析需求,本文采用Greenplum分布式数据库[4-5]存储脉冲星信号。在数据库中对数据计算分析通常使用SQL语句,但SQL语句不便于实现复杂的算法,例如快速傅里叶变换等科学分析算法,而用户自定义函数(UDF)可以满足这一需求。本文实现了UDF形式的快速傅里叶变换算法,为了提高算法效率,对算法的执行做了进一步的优化。
在Greenplum数据库集群中有多个segment实例,每个实例能够并行执行一部分任务。文献[6]设计了并行结构的FFT算法,本文同样对FFT进行了并行化设计,使每个实例能够并行计算并得到一部分结果,从而提高算法执行效率。另一方面,集群中数据分布[7]也可能影响算法性能。Greenplum将数据分布到各个节点中,当在某个节点上执行UDF时,由于节点的负载等不同,会导致不同的性能。为了使UDF算法执行性能达到最优,本文做数据重分布。文献[8]根据网络传播元组数目,重分布节点元组,从而提高表连接性能。本文是根据当前节点的数据分片大小、负载等因素重分布元组数据,能够较大地提高FFT的执行效率。
1 预备知识
1.1 Greenplum分布式数据库
分布式数据库[9-10]是通过网络将物理上分散的多个数据库单元连接起来组成的一个逻辑上统一的数据库。每个数据库单元相当于一个数据库实例,它存储数据且并行执行查询。在查询时[11],集群中的各数据库实例能够并行执行一部分查询任务,从而提高查询效率。
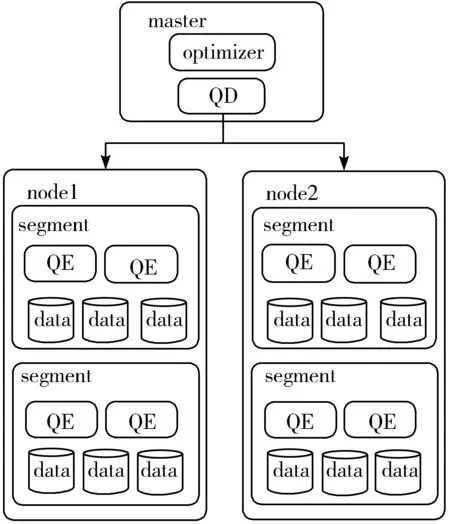
图1 Greenplum架构
Greenplum是基于PostgreSQL 8.X的MPP分布式数据库。MPP[12](shared nothing架构)指有2个或更多个处理器协同执行一个操作的系统。每个处理器都有自己的内存、操作系统和磁盘。图1是Geenplum的架构图。
Greenplum集群中的节点分为2类,一类是master节点,一类是node节点,node节点为物理节点,每一个node节点上都有多个数据库实例segment,负责存储与查询数据。当一个查询到来时,master节点上的优化器(optimizer)负责生成查询计划,而查询调度器(QD)会以slice的形式下发查询任务到每个数据节点,数据节点收到查询任务后,创建查询执行器(QE)进程执行任务。Greenplum将一个查询计划切分成多个slice来执行,多个查询计划并行执行。本文的UDF通过QE执行。
1.2 UDF技术
在编写应用程序的时候,传统的方法是让服务器应用程序的处理逻辑尽可能地被推送到客户端,而程序处理的数据也需要通过外部网络从数据库中读取然后推送到客户端。本文的方法是把计算、数据操作全部转移到一个位于服务器上的UDF里面,然后直接在数据库服务器中执行该UDF。UDF不仅便于设计更加复杂的算法,同时还消除了数据在客户端与服务器之间传输的过程,减少了算法执行的时间。
Greenplum中的UDF能够提供强大的扩展能力,比如能够添加数据类型、创建新的索引等。用户可以使用UDF实现内置函数不提供的功能和完成复杂算法。UDF可以用多种语言实现,比如Python、Perl等一些插件式的脚本语言。但脚本语言在某些情况下存在缺陷,一方面,当执行相同的算法时,大多数脚本语言会比C代码运行得慢;另一方面,当遇到函数要被每个查询调用成千上万次的情况,那么运行过程会出现各种超负荷运作,如函数调用、参数与返回值在脚本语言间的转化等。基于此,本文采用C语言实现UDF形式的快速傅里叶变换算法。
2 数据重分布
Greenplum在进行数据分布[13]时是根据表的分布键按照分布策略把表数据分散到不同的segment实例。常见的分布策略包括哈希分布和随机分布。哈希分布[14]是根据指定的分布列计算该列对应的每一行数据的哈希值,并映射行数据至相应的segment实例。随机分布指记录随机分散数据,相同的记录可能分布到不同的segment。本文采用的数据分布策略为哈希分布。但哈希分布仅考虑了数据的分布存储,没有考虑分布对查询的影响。例如当一个节点的CPU利用率很高时,位于该节点上的segment的查询执行效率会极大地下降。基于此,在执行查询前,本文对数据重分布,即根据当前各segment的负载和数据分布情况对表记录重新调整分散,从而加快后续查询的执行速度。
2.1 数据重分布方案
在调整数据分布前,需要确定当前数据分布的状态,一个表的数据分布通常有如图2所示的几种情况。

图2 数据分片
在图2中,node1、node2、node3、node4为Greenplum的4个物理节点,与图1的node1和node2类似。seg0,seg1,…,seg15为16个segment,与图1中的segment类似,图2中的a1~a16、b1~b4、c1~c4、d1~d3分别为表a、b、c、d的数据分片,例如表b有4个数据分片b1、b2、b3、b4,分别分布在seg2、seg6、seg10、seg14。数据分布分为以下2种情况:
1)数据均匀分布在各个segment上。
数据表a的记录分布在集群中的所有segment中,这种情况不做处理,直接运行查询。
2)数据分布在多个segment上。
如图2中的表b、c、d,数据分布在16个segment中的少数几个segment中。例如表c的数据分布在seg4、seg5、seg8和seg12,这种情况需要根据代价判断是否需要做数据重分布。以数据表d为例,表d的数据分片为d1、d2、d3,分别位于seg4、seg8、seg12上。首先分析数据分片d1,d1位于seg4上,则需要计算d1均匀分布到除seg8、seg12外的其他14个segment的代价,一共有n种情况:
(1)
2.2 计算代价
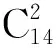
C=负载+时间
(2)
代价可根据节点当前的负载[15]和预计所需时间得到,比如在计算I/O代价时候,需要评估节点的I/O负载,还需要估算数据从磁盘读出和写入磁盘的时间,然后根据这2个维度的值得出代价。
2.2.1 计算CPU代价
计算CPU代价时,首先需要得到系统当前的负载,负载越高,代价越大,估算负载的公式如下:
(3)
公式(3)对CPU当前的负载做归一化处理,LCPU表示系统当前的负载,利用uptimie命令得到,φmin表示系统的最小负载,φmax表示系统的最大负载,由于本文的实验环境中的机器的CPU为4核,所以φmax一般大于4。由于φmin可以为0,所以能够得到公式(3)的右半部分。
在得到CPU的负载后,还需要估算CPU处理记录的代价,计算公式如下:
(4)
公式(4)做归一化处理,α为当前segment的记录条数。βmin表示segment的最小记录条数,βmax表示segment的最大记录条数,对于d1来说,这个值为2个segment上存储的记录总数,同样由于βmin可以为0,所以,能够推导出等式的右半部分。
在得到负载和耗时的值之后,便可以计算CPU的代价:
(5)
由于负载对CPU代价影响较大,所以负载乘以100。从上述公式可以看出CPU的负载越大,CPU代价越大,同样待处理的记录条数越多,CPU的代价也越大。
2.2.2 计算I/O代价
计算I/O代价同样需要得到负载和时间2个维度的值。负载能够直接通过iostat命令得到,磁盘的使用率越高表示I/O的负载越大,I/O的代价LIO也就越高。假设从磁盘读取的数据量为γr,向磁盘写入的数据量为γw,读磁盘的速率为δr,写磁盘的速率为δw,则可得到代价为:
(6)
在得到2个维度的代价以后,则可计算I/O的代价:
(7)
上述公式中的100,同样是为扩大负载对代价的影响。公式(7)表示当负载越大,读写磁盘的数据越多,I/O代价越大,反之,越小。
2.2.3 计算网络代价
计算网络代价与计算I/O代价类似,首先通过命令netstat得到网络负载的代价Lnet,接着计算通过网络传输数据的代价。假设传输的数据量为n×m kB,网络的带宽为ξ,对于传输数据的代价为:
(8)
由此得到网络总代价为:
(9)
可见,网络负载越高,传输的数据量越多,则网络代价越大。
2.2.4 计算平均等待时间
在得到了CPU、I/O和网络的代价,总代价为上述3个代价之和,如果对于2种不同的方案,总代价C相同或者相差不大时,还需要判断每个segment的任务平均等待时间Tavg。该值通过公式(10)计算得到:
Tavg=(Q1+Q2+Q3+…+QZ)/z
(10)
公式(10)中的Q1,Q2,…,Qz为segment中在等待队列中的查询的等待时间,而z表示等待任务的个数。
2.2.5 计算总代价
一种方案的总代价为:
C=CCPU+CIO+Cnet
(11)
总代价即为CPU、I/O和网络代价之和。在得到每种方案的总代价以后,比较所有方案的代价,采用代价最小的方案。如果待比较的2种方案的代价之差小于σ,则比较2种方案中待迁移到的segment上任务的平均等待时间Tavg,其中σ通过实验根据经验得到。下面是对于方案τ1和τ2,判断采用哪种方案的算法,C1、C2表示2种方案的代价,T1、T2表示2种方案中segment的总平均等待时间。算法1为选择方案算法。
算法1选择方案算法
if(C1=C2or abs(C1-C2<σ){
if(T1 use τ1 }else{ use τ2 } }else if(C1 use τ1 }else{ use τ2 } 上述算法能够得到一种代价最小或代价与平均等待时间都较小的方案,该方案能够最大程度地提高快速傅里叶变换执行效率。 根据第2章得到的数据分布方案对数据进行重分布后,还需要设计并行化的快速傅里叶变换算法。 快速傅里叶变换是对离散傅里叶变换(DFT)的改进,DFT的计算过程如下。 给定向量A=(a0,a1,…,an-1),DFT将A变换为B=(b0,b1,…,bn-1),变换的过程为: (12) 式(12)中的w=e2πi/n,式(12)表示的含义写成矩阵形式为: DFT的另外一种形式为: (13) 举一个具体的例子:对于一个4点的向量X=[2,3,3,2],DFT的计算过程如下: 图3 FFT算法 从图3可以看到,对于一个初始向量X[n],可以分段得到结果x[k],因此,可以通过在Greenplum中的各个segment并行执行得到部分结果,然后在master上汇总结果并返回。 根据快速傅里叶变换的算法原理,能够设计多进程并行执行的FFT[16-18]。由于数据存储在Greenplum中,可以利用Greenplum的分布式特性,通过让多个segment并行运行来实现多进程执行的效果。利用Greenplum的UDF实现快速傅里叶变换的算法设计见算法2。 算法2快速傅里叶变换的分布式并行执行 master: get_situation(); for(i=0;i { w[i].r=cos(i*2*PI/wLength); w[i].i=sin(i*2*PI/wLength); } parallel segment: cal_partial(); send_partial(); master: recv_gather(); 上述算法共分为3个步骤: 1)在master上执行准备工作,例如得到数据分布情况、初始化旋转因子数组等。 2)在segment上执行快速傅里叶变换。 3)在master节点上汇总各并行的segment结果并返回给客户端。 算法的主要函数说明如下: 1)get_situation()。得到数据的分布情况,包括:数据分布在几个segment上,每个segment有多少条记录等。在得到数据的分布情况后,接着初始化旋转因子数组,并把该数组发送给各segment。 2)cal_partial()。每个segment执行具体的快速傅里叶变换,该函数能够得到最终结果的一部分。 3)send_partial()。每个segment得到一部分结果以后,把结果送给master节点。 4)recv_gather()。接收各segment的结果并汇总,返回给客户端。 本文工作中采用的Greenplum版本为5.0.0-alpha+79a3598。集群共有5个节点,1个主节点和4个从节点,从节点主要用来存放数据并执行查询,主节点则负责分配查询和汇总结果。主节点的硬件配置为32 GB的内存,CPU为4核Intel(R) Xeon(R) CPU E5-2630 v2@2.60 GHz,从节点的内存16 GB,CPU的核数和型号与主节点相同,在每个从节点中有4个数据库实例。主节点和从节点的操作系统均为CentOS 7.4,Linux内核版本为3.10。 本文的测试数据为用Python模拟生成的脉冲信号,数据量最大为10 GB,在数据库中使用列存储方式存储数据。使用列存储有利于数据压缩,并且能减少查询的数据量。 为了验证DoFFT算法并行执行的效果,实验比较当所有数据存储于集群中的一个segment中与均匀存储于所有segment时的FFT执行效率。数据量范围为1 GB~10 GB。性能结果如图4所示。 图4 并行FFT效率对比 从图4可以看出,DoFFT算法能够极大提升FFT的效率,并且随着数据量的增多,提升效果也更明显。 上节比较了DoFFT并行化算法对FFT效率的提升,本节比较DoFFT对于不同的环境负载的优化效果。 4.2.1 CPU CPU对执行效率的影响主要在于,若某个segment的CPU负载很高,则会降低该segment上FFT的执行效率。本实验中创建一个高负载的环境,使CPU的平均负载高于4,对比该执行环境下,直接执行FFT所用时间与使用DoFFT算法后的时间,如图5所示。 图5 CPU影响 从图5可以看出,在每个数据量级别下,DoFFT算法对FFT性能都有2倍左右的性能提升。 4.2.2 I/O I/O对FFT执行效率的影响主要来自于节点的I/O负载和I/O带宽。由于集群中的节点具有相近的I/O带宽,所以主要比较DoFFT算法对I/O负载的优化效果。结果如图6所示。 图6 I/O影响 从图6可以看出,在小数据量时,DoFFT算法提升效果并不明显,但随着数据量的增加,效果越来越明显。 4.2.3 网络 Greenplum在执行FFT时,数据会在网络中传输,网络的负载和带宽对性能会产生一定影响。图7展示了DoFFT基于网络因素对FFT的优化效果。 图7 网络影响 从图7可以看出,DoFFT算法能够小幅度地提高性能,但较CPU和I/O,对网路的提升效果不明显。 4.2.4 平均等待时间 分布式数据库中的segment执行的任务数会不同,任务平均等待时间也会不同,平均等待时间越长,处于等待队列中的查询被调度执行所需的时间也就越长。图8展示了当某些segment中执行较多任务时,DoFFT的优化效果。 图8 平均等待时间影响 从图8可以看到,平均等待时间同样能够小幅地提升效率。 4.2.5 实验总结 上述的实验结果表明,DoFFT算法能够不同程度提高算法的执行效率。DoFFT的并行化对FFT执行提升效果最明显。在各影响因素中,对CPU和I/O优化的的提升效果较明显,对网络和平均等待时间优化的提升较小。 为提高快速傅里叶变换算法在分布式数据库中执行的效率,本文提出了DoFFT算法。算法首先对Greenplum中的数据进行重分布。Greenplum在存储数据时,会使用哈希分布或随机分布策略分散表数据至各个segment实例,而在实际环境中,每个segment的CPU、I/O等负载不同,硬件配置环境不同,会造成UDF形式的FFT算法在执行时达不到最优性能。DoFFT算法以每个segment的负载、处理时间等量化为代价,采用一种代价最小的方案对数据做重分布。并且,为进一步提升FFT执行效率,DoFFT算法还利用Greenplum中各个segment实例并行地执行FFT。实验结果表明,DoFFT算法能够较好地提升FFT在分布式数据库中执行的性能。 参考文献: [1] Cochran W, Cooley J, Favin D, et al. What is the fast Fourier transform?[J]. Proceedings of the IEEE, 1967,15(10):1664-1674. [2] 刘东亮, Demorest P, 南仁东. 基于CUDA的相干消色散算法实现与测试[J]. 科学技术与工程, 2010,10(8):1947-1950. [3] 徐永华,李纪云,张颖倩,等. 相干消色散脉冲星观测系统的研究[J]. 天文研究与技术, 2015,12(4):480-486. [4] Caragea G C, Garciaalvarado C, Petropoulos M, et al. Total operator state recall—Cost-effective reuse of results in Greenplum Database[C]// IEEE International Conference on Data Engineering Workshops. 2013:44-49. [5] Antova L, El-Helw A, Soliman M A, et al. Optimizing queries over partitioned tables in MPP systems[C]// Proceedings of 2014 ACM SIGMOD International Conference on Management of Data. 2014:373-384. [6] 丁顺英. 基于并行结构的FFT算法的软硬件设计与实现[D]. 哈尔滨:哈尔滨工业大学, 2012. [7] Cheng Long, Li Tao. Efficient data redistribution to speedup big data analytics in large systems[C]// IEEE International Conference on High Performance Computing. 2017:91-100. [8] Polychroniou O, Sen R, Ross K A. Track join: Distributed joins with minimal network traffic[C]// Proceedings of 2014 ACM SIGMOD International Conference on Management of Data. 20141483-1494. [9] Özsu M T, Valduriez P. Distributed database systems: Where are we now?[J]. Computer, 2002,24(8):68-78. [10] Rothnie J B, Goodman N. A survey of research and development in distributed database management[C]// International Conference on Very Large Data Bases.1977:48-62. [11] Yu C T, Chang C C. Distributed query processing[J]. ACM Computing Surveys, 1989,16(4):399-433. [12] Dewitt D J, Gray J. Parallel database systems:The future of database processing or a passing fad?[J]. ACM Sigmod Record, 1990,19(4):104-112. [13] Garcia-Alvarado C, Raghavan V, Narayanan S, et al. Automatic data placement in MPP databases[C]// IEEE International Conference on Data Engineering Workshops. 2012:322-327. [14] Shen Yuxia. Distributed storage system model design in Internet of things based on hash distribution[J]. International Journal of Security & Networks, 2017,12(3):141.. [15] Curino C, Jones E P C, Madden S, et al. Workload-aware database monitoring and consolidation[C]// ACM SIGMOD International Conference on Management of Data. 2011:313-324. [16] Große P, May N, Lehner W. A Study of Partitioning and Parallel UDF Execution with the SAP HANA Database[EB/OL]. https://www.researchgate.net/publication/266660040_A_study_of_partitioning_and_parallel_UDF_execution_with_the_SAP_HANA_database, 2018-03-13. [17] Taboada J M, Araujo M G, Basteiro F O, et al. MLFMA-FFT parallel algorithm for the solution of extremely large problems in electromagnetics[J]. Progress in Electromagnetics Research. 2010,101(2):350-363. [18] Chu E, George A. FFT algorithms and their adaptation to parallel processing[J]. Linear Algebra & Its Applications, 1998,284(1):95-124.3 快速傅里叶变换的并行实现
3.1 快速傅里叶变换

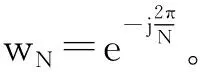

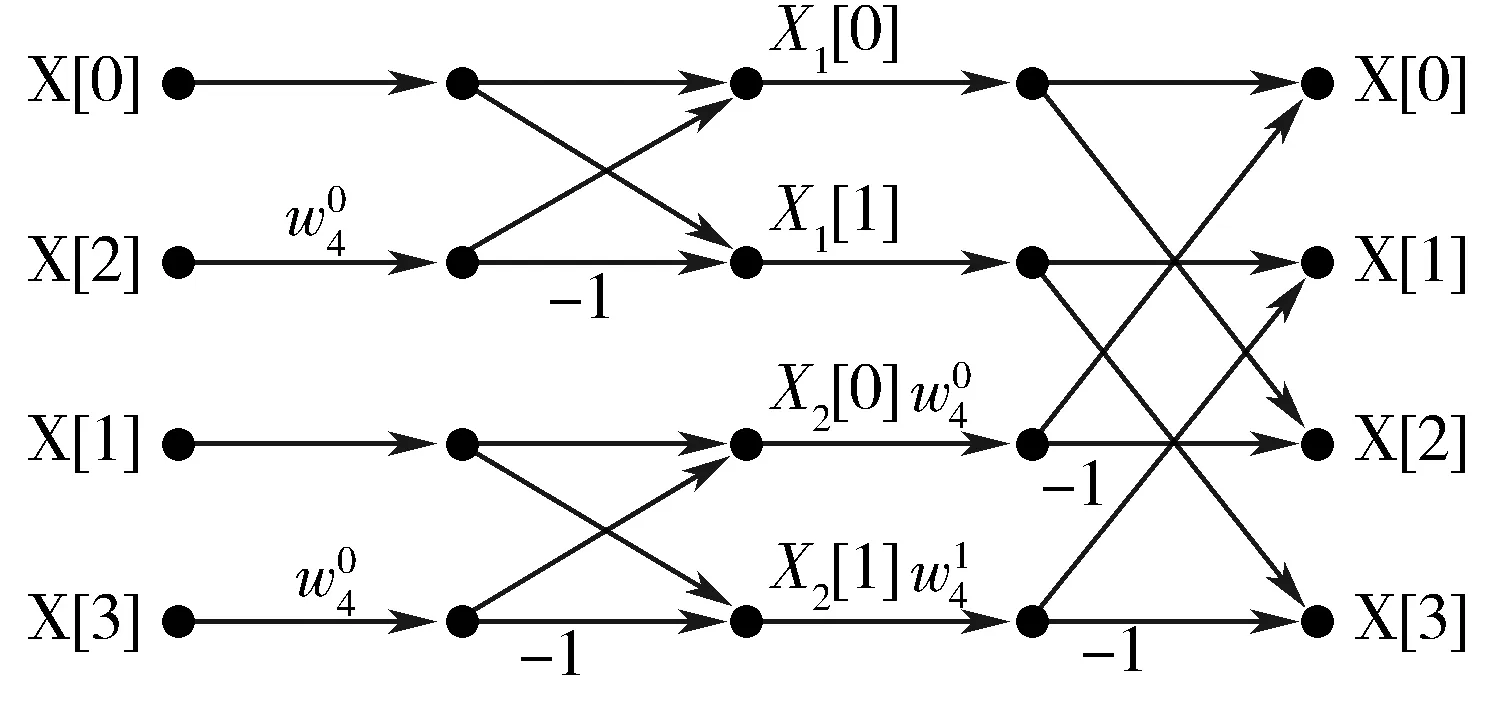
3.2 分布式并行执行
4 实验及结果分析
4.1 并行化执行对效率的影响
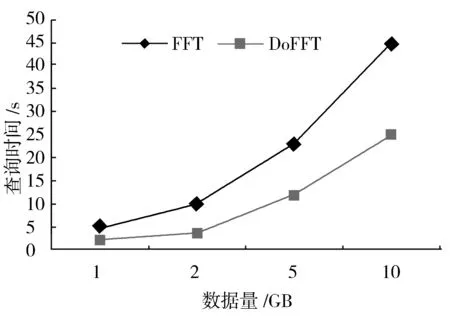
4.2 执行环境对效率的影响




5 结束语
——国外课堂互动等待时间研究的现状与启示

