基于量纲分析法的分段嗣后充填法采空区顶板稳定性判别

姜桂鹏，杨桂涛，刘新刚

（甘肃省合作早子沟金矿有限责任公司，甘肃 合作 747000）

由于设备和技术所限，20世纪我国有90%以上的大型地下铁矿采用崩落法进行开采，崩落法具有快速高效的优点，但长期使用则会引起严重的地表塌陷，造成的环境破坏以及对矿区居民生产生活带来安全威胁[1，2]。随着开采深度的增加，崩落法造成的地表移动范围日益扩大，为保护地表，避免引起灾难性的地表塌陷事故，采用充填法替代崩落法开采地下矿石成为采矿技术发展的必然趋势[3-5]。尤其随着开采深度的增加，分段嗣后充填法将逐渐成为主要的开采方法。

分段空场嗣后充填法采空区跨度往往较大，且岩石的矿压强度远远大于抗拉强度，因此，在上覆压力的作用下，顶板更容易发生破坏，顶板成为采空区稳定性的控制因素。对采空区顶板的稳定性进行正确判别，具有重要的工程意义。

目前关于采空区顶板稳定性判别方法主要包括数值模拟、理论分析及现场监测等[6，7]，张敏思[8]等基于RFPA数值模拟方法，对采空区顶板安全厚度和临界跨度进行了分析；柳小波[9]等基于ABAQUS有限元数值模拟对采空区顶板破坏机理及安全厚度进行了研究；王金安，孙琦[10，11]基于粘弹性理论及薄板对顶板矿柱的流变力学模型进行了研究，现有的顶板稳定性评价方法在工程实践中由于分析和计算复杂而不方便应用[12]，因此需要寻求一种便于工程应用的模型分析顶板的稳定性。

在开采技术条件一定的情况下，采空区顶板厚度与跨度的厚跨比是影响顶板稳定性的主要因素[13，14]。量纲分析是建立数学模型的一个有力工具，具有简单实用的特点。本文基于量纲分析法建立了分段空场嗣后充填法采空区顶板稳定性判别数学模型，并基于具体工程案例，结合数值模拟技术对该方法进行了验证。

1 工程背景

某铁矿是我国著名的大型地下金属矿山，矿体呈南东45°走向，倾角约30°，区内矿体宽度大，最宽处达120m以上，是典型的缓倾斜厚大矿体。自1978年建矿以来，一直采用无底柱分段崩落法开采。矿体赋存的工程地质、水文地质和地表地形条件复杂，缺乏对崩落法开采过程中矿体上部围岩错动机理的研究和塌陷规律的监测，出现了大量的地表塌陷情况，一直是困扰该铁矿安全生产和技术管理的重大难题。

随着开采深度增加，崩落法开采引起的地表塌陷越来越大，后续开采深度还会进一步增加，必须用充填法来替代现有的崩落法进行开采。该铁矿-500 m以下矿石及矿体顶底板岩石为中等稳固，因此选择分段空场嗣后充填法进行开采，由于上部存在大量的崩落废石，因此，进行采空区顶板稳定性设计及分析时，必须考虑上覆岩层的压力。

该铁矿矿体厚度较大，矿房垂直走向布置。沿矿体走向上将矿块划分为矿房和间柱，矿房和间柱交替回采。为了崩落法转分段空场嗣后充填法的顺利过渡，采场的主要参数不宜作重大改变。

因此采用分段空场嗣后充填法进行开采时，阶段高度、矿块排列方式和矿块尺寸都不做调整。

2 顶板稳定性量纲分析数学模型

2.1 量纲分析法简介

物理量的量纲反映了给定物理量与单位制基本量之间的关系，其比例系数等于1，它是相应基本量指数的乘积。因此，量纲可以用来分析物理量之间的关系，这种方法称为量纲分析。

通常，一个物理量的量纲是由质量、长度、时间、温度一类的基础物理量的量纲结合而成。长度单位用L表示，质量单位用M表示，时间用T表示、温度用K表示。进行量纲分析时，物理定律必须跟其计量物理量的单位无关。任何方程式，两边的量纲必须相同。其中，π定理是一种常用的量纲分析法。

设是与量纲单位无关的物理定律，X1，X2，…，Xn是基本量纲，，则的量纲如式1所示。

量纲矩阵记作：，若，则线性齐次方程组Ay=0有m-r个基本解，为：

且有，与等价，其中F为一未知函数。

2.2 顶板稳定性量纲分析法计算步骤

（1）总结归纳采空区顶板稳定性影响因素，记为，根据影响因素的物理意义及量纲确定基本变量，记为：；

（2）写出qj的量纲：

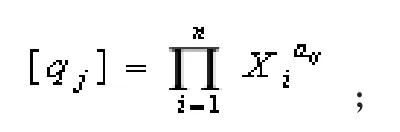
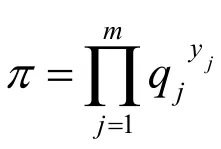
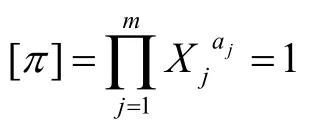
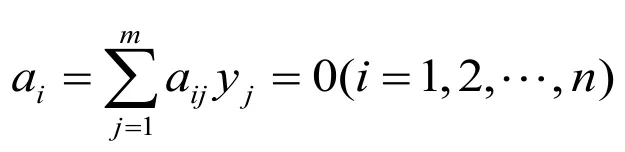
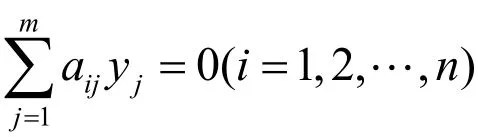
矩阵称为量纲矩阵，若A的秩rankA=r，则线性齐次方程组有m-r个基本解为：

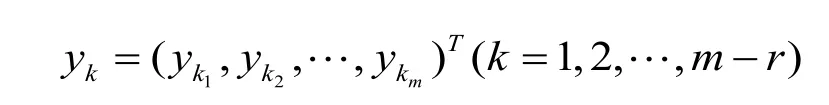
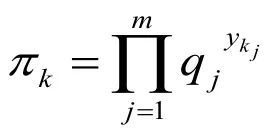
则为无量纲的量；

（6）由解出物理规律。

2.3 分段嗣后充填法采空区顶板稳定性影响因素

对于分段嗣后充填法而言，由于顶板跨度大，易出现拉应力，而造成失稳，因此顶板成为采空区安全的关键因素之一。根据采空区特点，影响采空区顶板稳定性的主要包括外部和自身结构因素。

对于外部因素，忽略爆破震动、地下水等的影响，因此，影响顶板稳定性的重要因素为上覆岩层的压力。由于地下采场往往较深，与上覆岩石的压力相比，顶板的自重是一个极小量，因此忽略顶板的自重，只考虑上覆岩层的压力。

根据顶板的几何特征，顶板的结构主要包括厚度及跨度，因此两者也是决定顶板稳定性的重要因素。顶板厚度越大，顶板越稳定，对顶板稳定性的贡献也就越大。矿房的跨度越大，顶板越不稳定，反之越稳定。

经上述分析，确定影响顶板稳定性的四个最主要的因素：上覆岩石的压力P、顶板的跨度W、厚度H及顶板中的应力σ。

表1 各影响因素的列表及符号

由于温度的对采空区顶板稳定性影响较小，因此选择质量[M]、长度[L]以及时间[T]作为基本量纲。利用基本量纲代换得出各影响因素的量纲，其量纲如表1所示。

2.4 顶板稳定性评价模型建立

根据上述分析可知，根据π定理，顶板稳定性影响因素满足关系式：

则每个因素的量纲分别为：

则有量纲矩阵为：

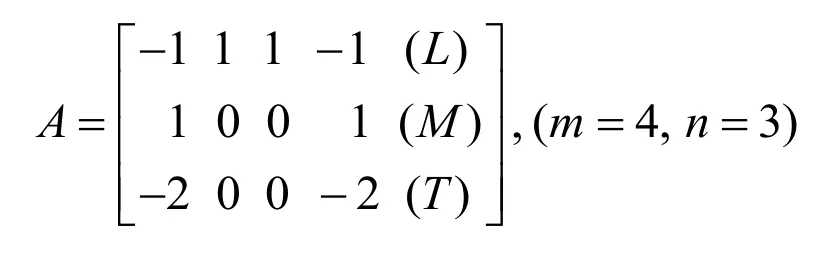
求得A的秩rankA=2，则可知Ay=0有2个基本解。求解线性方程组，可得：

由π定理，可导出2个无量纲量π1，π2，即：

由等价关系可得：

对上式进行变换可得：

式中，为未定函数。

工程中顶板中的应力测量较为复杂，与应力测量相比顶板的位移测量更为简单。利用应力、应变、位移相互之间的关系，将顶板中的应力转换为应变，用应变表示顶板的稳定性。

岩石力学中认为岩石的破坏分为塑性破坏和脆性破坏。工程中开挖造成的破坏多为脆性破坏，因此计算时将顶板作为弹性材料。

松散岩石主要造成顶板下表面的拉破坏，由于岩石的各向异性且岩石的抗拉强度远小于抗压强度，因此在计算拉破坏时需要将岩石弹性模量弱化。式中E为弹性模量。如式7所示。

式中，为顶板应变；为简化参数，

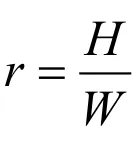
影响顶板中应变大小的主要因素是厚跨比r。若顶板的最大允许应变[ε]，将最大允许应变作为一个应变阀值代入式可得顶板稳定性判断关系式：

根据式可确定顶板的临界厚跨比，从而确定采空区的稳定性，并指导矿房设计。

3 工程实例分析

基于有限元理论，对采空区顶板的应力及应变进行计算。

3.1 采空区顶板数值计算模型及计算

3.1.1 数值模型构建

采场垂直矿体走向布置，采用“隔一采一”的方式进行回采，阶段放矿、阶段充填，取连续的3个矿房作为模拟对象。模型尺寸长×宽×高为200m×200m×200m，数值模型如图1所示。

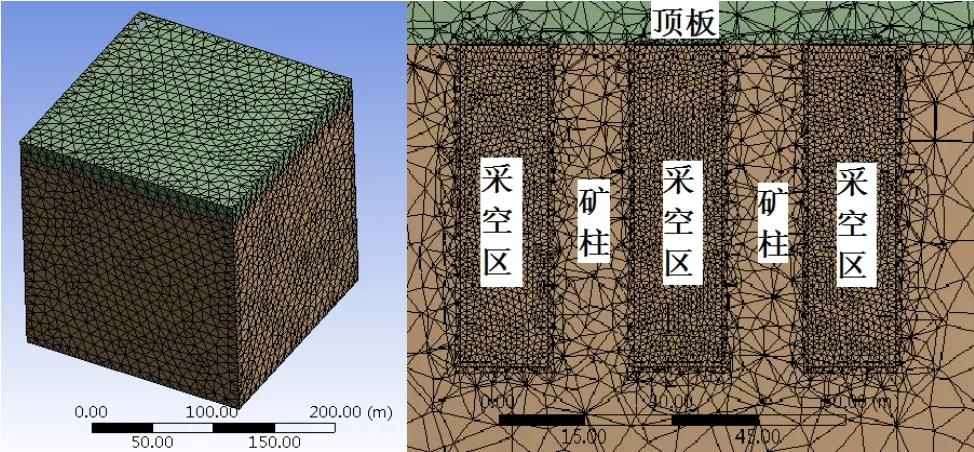
图1 分段空场嗣后充填法数值模拟模型

3.1.2 边界条件及参数选取

（1）材料物理力学参数

模拟对象是矿石。采用用摩尔-库伦准则计算。计算中涉及到的矿石物理力学参数如表2所示。

表2 矿石物理力学参数表

（2）初始地应力场

该铁矿上部采用无底柱分段崩落法，采区塌陷后在空区有松散的岩石填充，基本无构造应力，因此初始应力场采用自重应力场，利用均布荷载替代上部松散的岩石。选取松散岩石的容重为2.1 g/cm3，则顶板的上部压力可等效为10.08 MPa。

（3）边界约束条件

模型中设置除上端面自由面外的其它各面位移均为0。

3.1.3 计算方案

由于岩体的抗拉强度一般远小于抗剪强度和抗压强度，因此，若顶板下表面的拉应力σ≤σt(σt为岩体的抗拉强度)，即可认为矿房顶板没有破坏。

在采场的长度和宽度方向的对称中心分别建一个path路径，用path路径统计采场顶部在长度和宽度方向的应力和应变。各向上path路径的起点和终点都在矿房顶板的端面上，路径以左边起点作为原点，与原点的距离为该点的坐标点，其path路径建立结果如图2所示。

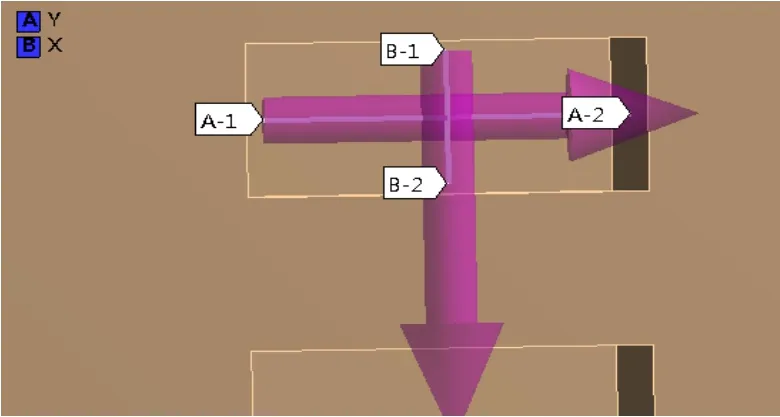
图2 Path示意图

在模型计算中，初始顶板厚度为10m，按照1m间隔进行递增至30m；初始矿房宽度为12m，按照1m间隔进行递增至25m。

3.2 采空区顶板应力及应变分析

经过模拟得到采场的位移云图和path路径上位移及应变，模拟结果如图3-图9所示。

图3为采场位移云图，据图可知，在三个进路中，中间矿房顶板的位移最大，另外两个矿房的顶板位移相较小。

图4和5为长度方向和宽度方向path路径上应变，据可知，在顶板上的应变除两端的几个点外，其它的各点应变成抛物线趋势变化。

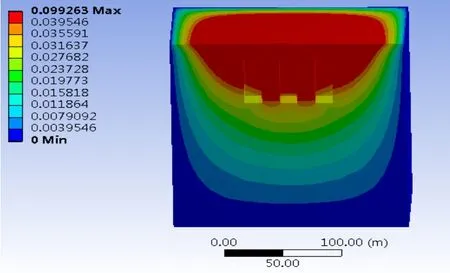
图3 采空区位移云图

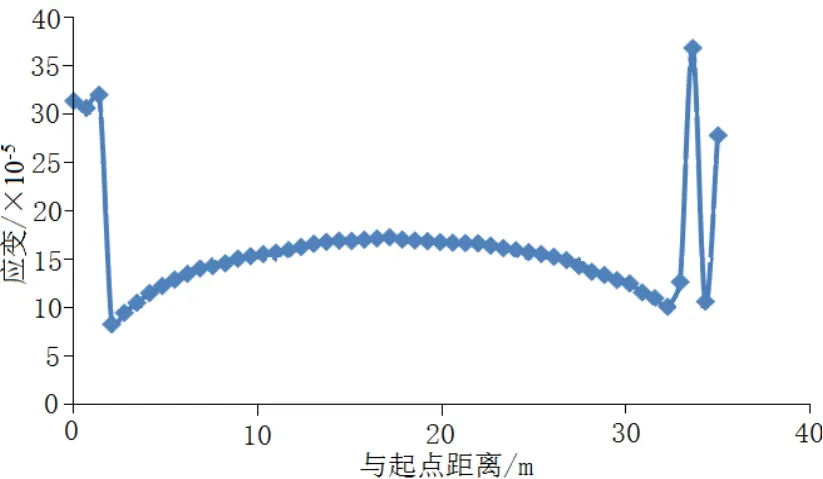
图4 长度方向上各点的应变

图5 宽度方向上各点的应变

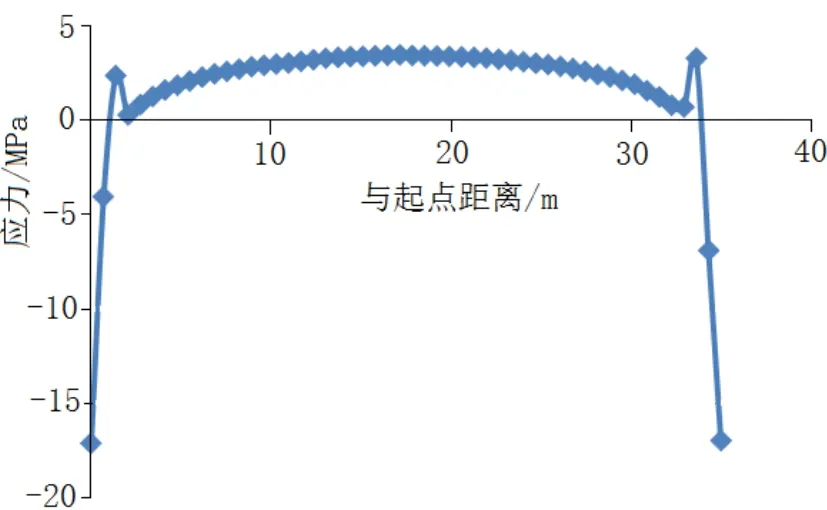
图6 长度方向各点的应力

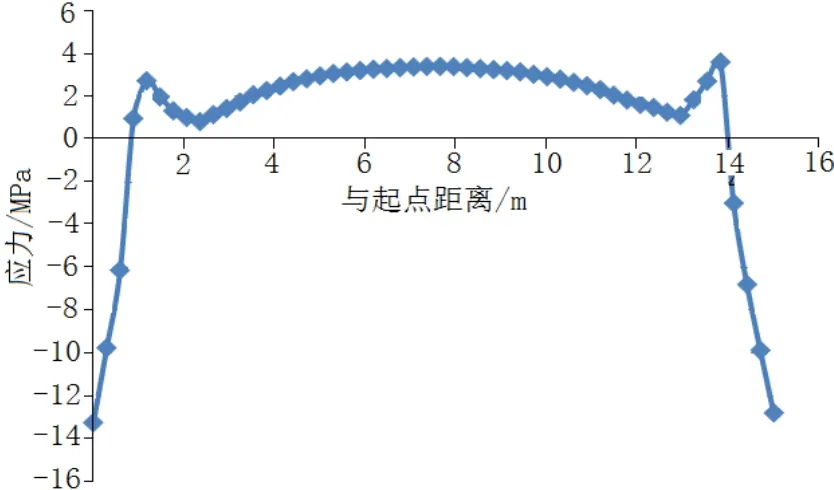
图7 宽度方向各点的应力

图6和7为长度方向和宽度方向path路径上应力，分析图可知，在路径上存在压力和拉力。在间柱上主要分布为压应力，在顶板上主要分布的是拉应力。端部位置的压力比拉应力的值大，造成在端部位置的压应变大于其他位置的拉应变。因此存在应变在路径两端波动。为了监测到顶板的最大拉应变，在建path路径时，将path起点和终点与端部拉开1m的距离。

查看数据知，在不同参数下，采场顶板的应变变化规律具有相似性。分析各组数据发现，最大位移、最大应变、最大拉应力存在的位置是相同的，其位置在顶板的中心处。

将各组参数中的最大应变最为判断顶板是否破坏的依据。各矿房跨度下顶板厚度与最大应变关系如图8所示。

根据图8可知，随着顶板厚度的增加，顶板的应变在逐渐减小，说明顶板越厚，其稳定性越好。同时随着矿房跨度的增加，顶板的应变逐渐增大，说明矿房跨度越大，其稳定性越差。因此如果需要矿房的顶板稳定，需要增加顶板的厚度，减小矿房的宽度。

图8 各顶板厚度下矿房跨度与应变的关系

考虑顶板厚跨比，得到了不同厚跨比与最大应变的散点图，并进行拟合，如图9所示。

根据无量纲分析可知，顶板厚度和进路宽度之间存在一定的关系，该关系对顶板的稳定性存在影响。通过拟合分析，得到分段空场嗣后充填法中厚跨比和顶板应变的关系为：

并得到其拟合度为0.84，则相关性为0.916。分析结果表明相关性较好，说明厚跨比与顶板应变的关系成立。

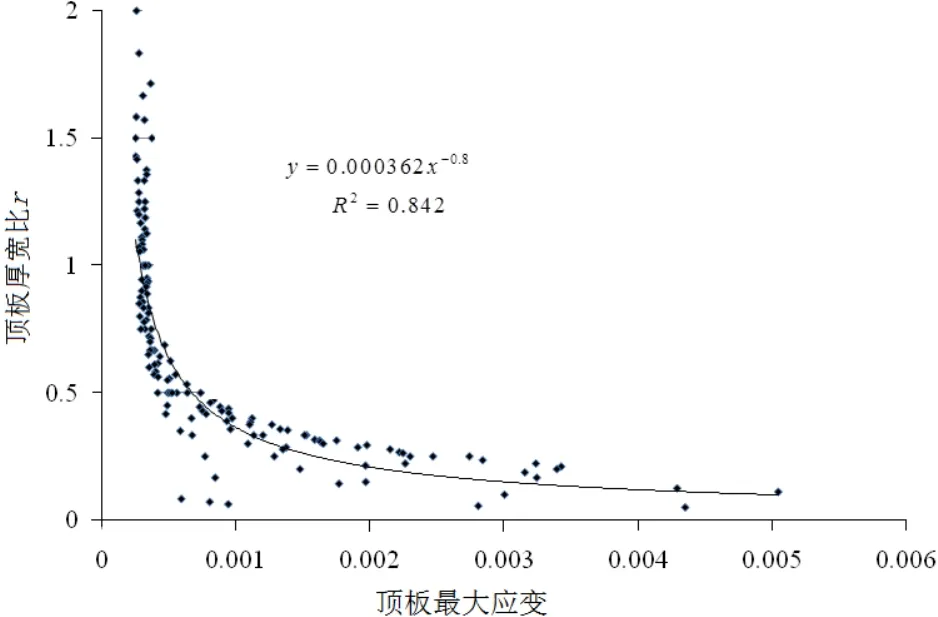
图9 厚跨比r与顶板应变ε的关系图

由胡克定律可知，应力与应变的具有以下关系：

式中：E为拉伸弹性模量；为应变。

根据公式计算得到，顶板允许的最大应变。当采场顶板的最大应变小于0.000321时，采场的顶板是稳定的。将顶板最大应变0.000321作为一个阀值代入公式中，则有：

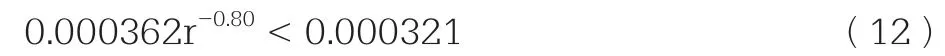
计算得到厚跨比r＞1.16，即表示厚跨比大于1.16时采场的顶板是稳定的。

若隔离矿柱厚度过大，可能会使矿山采掘失衡，造成资金闲置。因此厚跨比的取值有一定的上限，根据该铁矿损贫率指标，厚跨比的上限值取2.5。

综合考虑顶板稳定性和矿山生产，厚跨比的取值为1.16＜r＜2.5。

目前该铁矿正在-520～-539 m分段3#采区进行分段空场嗣后充填法的工业试验。实际生产过程中，由于采空区暴露面积较大，因此无法对顶板进行变形监测，只能通过观察采空区是否有冒落、垮塌来进行判断。现场工业试验表明，表明采空区顶柱处于稳定状态。该铁矿的工程试验检验了本文方法的有效性。

4 结论

本文分析了分段嗣后充填法采空区顶板的稳定性影响规律，采用量纲分析法建立了稳定性判别数学模型，结合有限元分析，对分段嗣后充填法采空区顶板稳定性进行判别，得到以下结论。

（1）根据该铁矿实际条件，影响目前分段嗣后充填法采空区顶板稳定性的因素包括顶板上覆岩层重量、顶板厚度、顶板跨度及内部的应力分布，基于量纲分析法中的π定理，建立了稳定性判别公式。

（2）结合有限元数值模拟分析，计算得到了顶板内部的应力及应变，代入顶板稳定判别公式中，并考虑实际生产需要，计算得到了稳定的临界厚跨比1.16＜r＜2.5，满足了工程需要。

（3）本文将量纲分析法应用到了金属矿山分段嗣后充填法采空区顶板的稳定性判别中，由于此法具有简单高效，准确率高的有点，可快速的被现场工作人员掌握。虽然目前考虑的因素较少，但仍然为一种较好的方法和手段。正如钱学森所说：运用量纲分析方法须将问题的基本物理内涵分析透彻，分析越深入，结论越有用；也需要进行多次试探和修正，最终得到符合实际的满意的结果。

[1]Brow n E T.Block Caving Geomechanics.Brisbane：Julius Kruttschnitt M ineral Research Centre,2003.

[2]SERYAKOV V.Calculation of stress-strain state for an overgoaf rock mass[J].Journal of Mining Science，2009，45(5)：420-436.

[3]宋卫东，杜建华，尹小鹏，等.金属矿山崩落法开采顶板围岩崩落机理与塌陷规律[J].煤炭学报，2010，35(7)：1078-1083.

[4]付建新，宋卫东，谭玉叶.考虑卸荷应力路径的深部采空区失稳局部能量释放判别准则[J].岩石力学与工程学报2016，35(2)：217-224.

[5]CHEN Q F，LIU Y X.Study on the size effect of goaf stability[J].Disaster Advances，2012，4(5)：1597-1601.

[6]张耀平，曹平，袁海平，等.复杂采空区稳定性数值模拟分析[J].采矿与安全工程学报，2010，27(2)：233-238.

[7]高峰，周科平，胡建华.充填体下矿体开采安全顶板厚度数学预测模型[J].岩土力学，2008，29(1)：177-181.

[8]张敏思，朱万成，侯召松，等.空区顶板安全厚度和临界跨度确定的数值模拟[J].采矿与安全工程学报，2012，29(4)：543-548.

[9]柳小波，彭建宇.采空区顶板破坏机理研究及安全厚度确定[J].金属矿山，2012(11)：5-8，13.

[10]王金安,李大钟,马海涛.采空区矿柱顶板体系流变力学模型研究[J].岩石力学与工程学报,2010,29(3)：577-582.

[11]孙琦,卫星,张淑坤,等.采空区顶板-矿柱体系蠕变损伤力学模型研究[J].安全与环境学报,2015,15(3)：120-123.

[12]高峰，周科平，胡建华.充填体下矿体开采安全顶板厚度数学预测模型[J].岩土力学，2008，29(1)：177-181.

[13]CHEN Q F，LIU Y X.Study on the size effect of goaf stability[J].Disaster Advances，2012，4(5)：1597-1601.

[14]赵康，赵奎，石亮.基于量纲分析的金属矿山覆岩垮落高度预测研究[J].岩土力学，2015,36(7)：2021-2026.