高寒地区围岩冻胀对已有裂缝隧道安全性的影响
王海龙,刘 畅
(河北建筑工程学院 土木工程学院,河北 张家口 075000)
隧道结构的安全性及耐久性是交通建设的重要问题。衬砌裂缝及冻害是主要的隧道病害。围岩冻胀是引起衬砌裂缝的外在原因之一。谭贤君等[1]通过岩体THMD耦合模型分析,提出冻融循环对隧道衬砌的影响较大;陈中秋等[2]研究得到隧道衬砌耐久性主要受围岩冻胀膨胀压力的影响;苑郁林等[3]提出了利用冻融敏感性评定隧道安全性;董长松等[4]针对隧道衬砌抗冻耐久性进行了研究。近年来,围岩温度场、应力场问题也成为热门研究方向,刘泉声等[5]研究了应力场、温度场、渗流场中岩体的分布规律;刘明等[6]提出围岩的稳定性在渗流场、温度场耦合作用下的不利因素;黄华南等[7]通过围岩温度场和应力场的耦合结构,得到衬砌结构的可靠性指标。围岩冻胀会对隧道衬砌产生附加应力,文献[8-9]探讨相关的补救措施。文献[10-17]研究了隧道衬砌裂缝对隧道结构的影响。国外,文献[18]通过数值分析研究了裂缝与夹杂物之间的影响关系,建立了关于裂缝尖端广义应力强度因子的相互关系和相互距离;文献[19]提出了一种自动化的基于无线多媒体传感器的地铁隧道裂缝监测方法。虽然国内外对于隧道结构病害方面的研究很多,但是对于围岩冻胀后产生的附加应力对带裂缝隧道衬砌的影响研究得较少,本文作这方面的探讨,主要考虑松动圈范围内的围岩冻胀力对衬砌的作用。
1 围岩冻胀对衬砌的作用分析
1.1 冻胀力
国内外对于围岩冻胀力的研究主要有冻融圈整体冻胀学说、存水冻胀学说、含水风化层冻胀学说。它们都存在各自的优点与不足。
本文结合冻融圈整体冻胀学说和存水冻胀学说,认为冻胀力主要由于孔隙中的冻胀水体产生冻胀变形与周围围岩、衬砌发生相对作用力而产生,其中围岩的孔隙率和冻胀区范围是影响冻胀力的主要因素。为了简化计算模型,将隧道衬砌和冻结围岩简化为2个同心且相互接触的圆环受力体系,如图1所示。
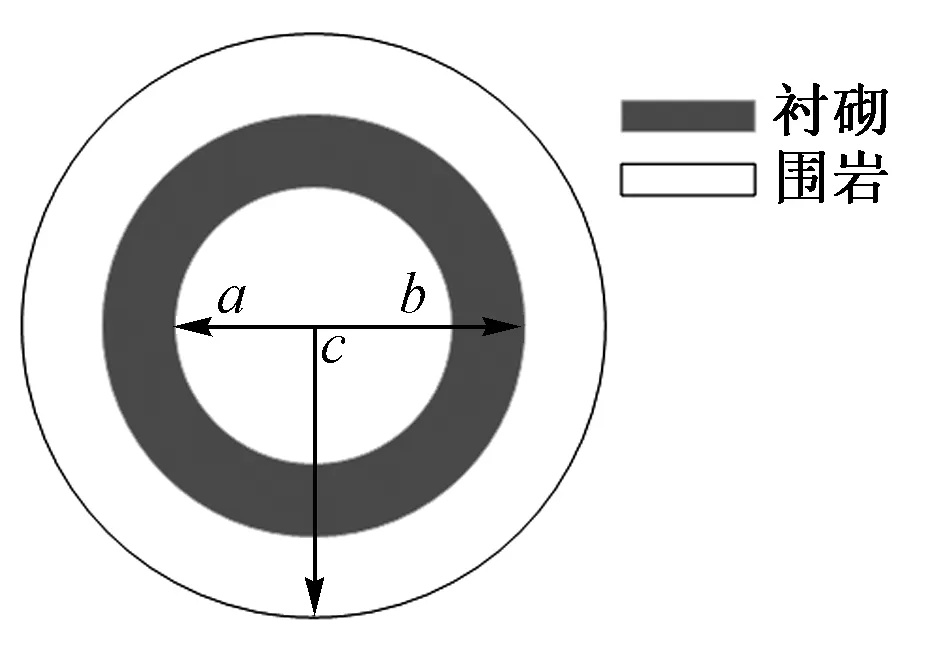
图1 隧道衬砌、围岩冻胀接触示意
为便于分析作出假定:①围岩是均质、各向同性的连续介质;②将围岩及衬砌简化为平面应变问题;③冻胀力主要由于冻结围岩中孔隙水结冰引起体积膨胀,从而与未冻围岩和衬砌发生挤压而产生;④冻胀围岩对周围围岩和衬砌的各个受压面的冻胀力大小相等;⑤冻胀围岩产生的冻胀力与受压面的作用力方向以法向为主,即冻胀力垂直各受压面。
根据以上假设,取单位体积的冻胀围岩,因为弹性单元的应力与变形存在线性关系且与时间无关,故可以将围岩与围岩、围岩与衬砌之间的接触简化为弹簧模型[13]。考虑冻胀围岩与衬砌、未冻胀围岩的相互约束关系,提出如图2所示的冻胀模型。
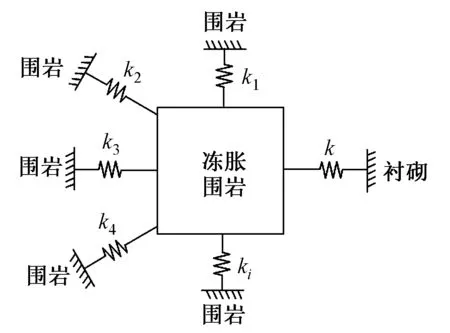
图2 冻胀模型
图2中,k为衬砌抗压刚度、ki为围岩第i个受压面的抗压刚度。依据假定可知冻胀力σf为
σf=k1Δ1=k2Δ2=…=kiΔi=kΔ
(1)
式中:Δ为衬砌的法向压缩变形;Δi为第i个围岩上的法向压缩变形。
从式(1)可以看出,任意一个受压面的抗压刚度为0时冻胀围岩的冻胀力为0。任意约束受压面的抗压刚度为0即受压面对冻胀围岩的约束力消失,冻胀围岩的冻胀变形将完全由此释放。
冻胀围岩体积增量可由图1得出,取隧道深度为单位长度,冻胀围岩整体体积增量ΔV为
ΔV=nαπ(c2-b2)
(2)
式中:n为围岩孔隙率,α为水变成冰的体积膨胀率。
单位体积增量ΔVm为
ΔVm=nαπ(c2-b2)/2c
(3)
又有
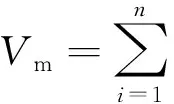
(4)
式中:Si为围岩第i个约束受压面的面积;S为受压衬砌面积。
将式(1)、式(3)带入式(4)中并化简得到
(5)
1.2 冻胀隧道衬砌内力
在等深均布荷载隧道中,简化力学模型见图3。
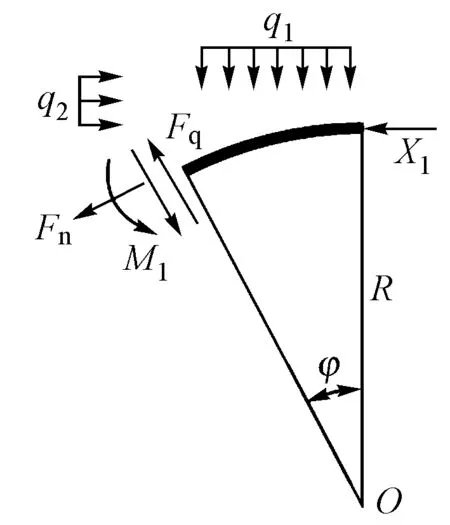
图3 隧道力学简化图
根据图3和式(5),参照JTG D70—2004《公路隧道设计规范》,可得
式中:γ为隧道上覆围岩重度;H为隧道埋深;Bt为坑道宽度;θ为滑面摩擦角;λ为侧压力系数,取1.142;φc为围岩计算摩擦角,取40°;Ht为隧道高度。
根据几何条件得
(8)
根据变形协调条件得
δ11X1+Δ1p=0
(9)
式中:X1为冻胀隧道某截面内力;δ11为X1方向单位力引起的该方向的位移;Δ1p为X1作用在结构的位移。
根据虚位移原理,将式(8)带入虚功方程得
式中:E为冻胀隧道衬砌弹性模量;G为剪切模量;A为衬砌截面面积;R为衬砌半径;I为截面惯性矩。
1.3 裂缝衬砌内力分配
已存在裂缝的衬砌刚度K根据文献[13]求得
式中:Ec为无裂缝衬砌弹性模量;Ic为无裂缝衬砌惯性矩;hc为衬砌裂缝深度;H为衬砌厚度;K0为初始刚度。
裂缝处的弯矩M与拱脚处弯矩M0关系式为
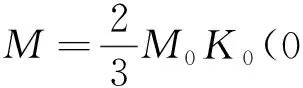
(14)
2 计算模型
一隧道位于河北省张家口市低山丘陵地区。当地冬季较为寒冷,最低气温达-25 ℃ 以下,冻土深度达1.4 m,属于高寒地区。采用扩展有限元方法进行模拟裂缝,为取可靠的工程安全系数,将围岩等级增大一级,设为V级围岩,衬砌结构为复合式衬砌,一次衬砌厚度为15 cm,二次衬砌厚度为45 cm。该隧道采用长度为4.5 m,直径为25 mm的中空砂浆锚杆,其间距为80 mm。隧道开挖宽度为16.71 m,隧道净高11.92 m,隧道计算纵深为1 m。由于衬砌初始状态带有裂缝,后续的运营中裂缝会继续开展,所以模拟为开展裂缝。
由于隧道为长细结构,因此沿着隧道纵向的变形和内力变化可以忽略不计,故采用二维平面模型进行模拟。计算模型采用线弹性平面应变模型,围岩假定为各向同性,围岩的初始地应力场仅考虑自重应力。计算中不考虑二衬中的局部配筋,假定围岩是连续均质介质,不考虑衬砌与围岩的接触关系。隧道中心位于模型中心,模型为四周约束。采用ABAQUS软件研究围岩冻胀对已有裂缝衬砌结构承载力的影响。将初始裂缝深度分别设为5,10,15 cm。主要对拱顶裂缝、拱腰裂缝和拱脚裂缝进行模拟分析,并比较不同裂缝规模受围岩冻胀的影响。围岩、衬砌参数分别见表1、表2。
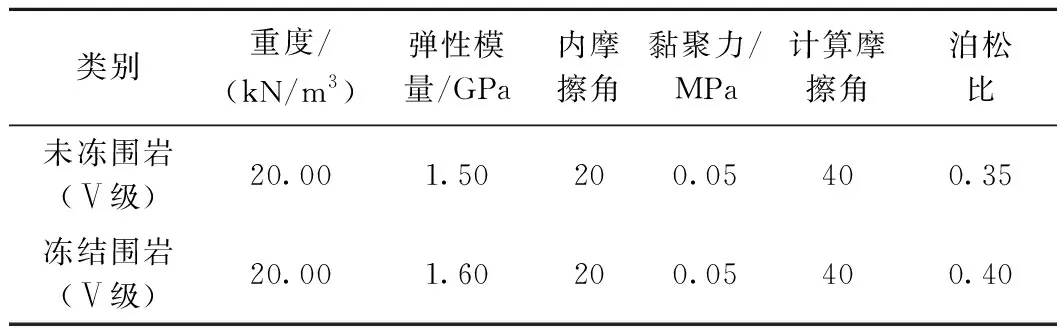
表1 围岩参数

表2 衬砌参数
3 参数分析
3.1 半径比
为研究冻结深度和隧道半径的相对关系,定义相对冻结深度系数α为冻结深度与隧道半径的比值,不同α值的衬砌状态见表3。
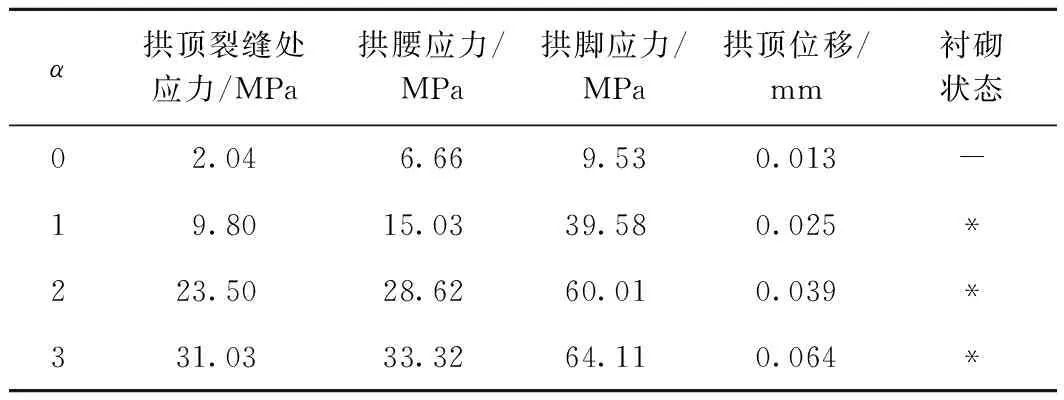
表3 衬砌状态
注:-表示衬砌为弹性状态;*表示衬砌局部进入塑性区。
由表3可知,相对冻结深度系数越大,衬砌应力越大,整个拱进入塑性区的面积越大,尤其表现在拱的上半部分,裂缝开展越长。在相对冻结深度范围内,围岩的松动圈因受冻胀而进入挤密状态,并在一定范围内向四周扩散,相对冻结深度系数越大,扩展得越多。主要原因是在-4 ℃以下,冰的体积膨胀,产生的膨胀力对衬砌和未冻胀区产生巨大的膨胀力从而导致岩体裂隙减小,岩石进入塑性流动区,处于高压状态。相对冻结深度系数越大松动圈缓冲作用越小,积累的能量越大,在边界区的相对变形达到一定范围时裂隙张开量和破碎程度都将增大,甚至出现断口,破坏了原有围岩的稳定性。在温度回升到0 ℃以上的时候,冰冻黏结力消失,围岩承载力将大幅下降,毛细水和承压水补充在新的空隙中,当温度再次降低,产生的冻胀力将比先前更大。但是经过数个冻融周期后,围岩的状态基本趋于稳定,除非冻胀周期加长,冻胀裂隙和冻胀力将不再增加。
3.2 局部冻胀
根据受力情况可以推得,对于拱结构在特定荷载情况下,拱的合理拱轴线主要线形为圆形、抛物线和悬链线。但是受地形环境等影响,隧道往往不会为均布受冻状态,故应考虑隧道衬砌局部受压时的受力情况。冻胀区划分如图4,分析工况见表4。
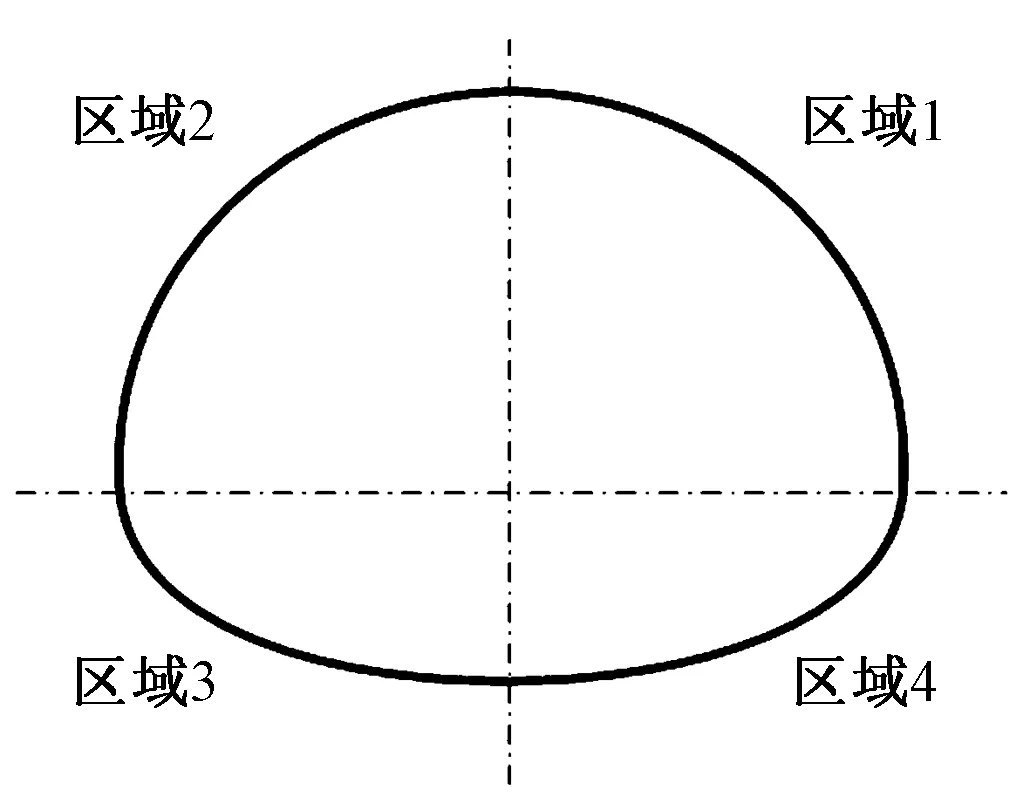
图4 冻胀区划分

工况1工况2工况3工况4区域1冻胀区域1和区域2冻胀区域1和区域4冻胀4个区域冻胀
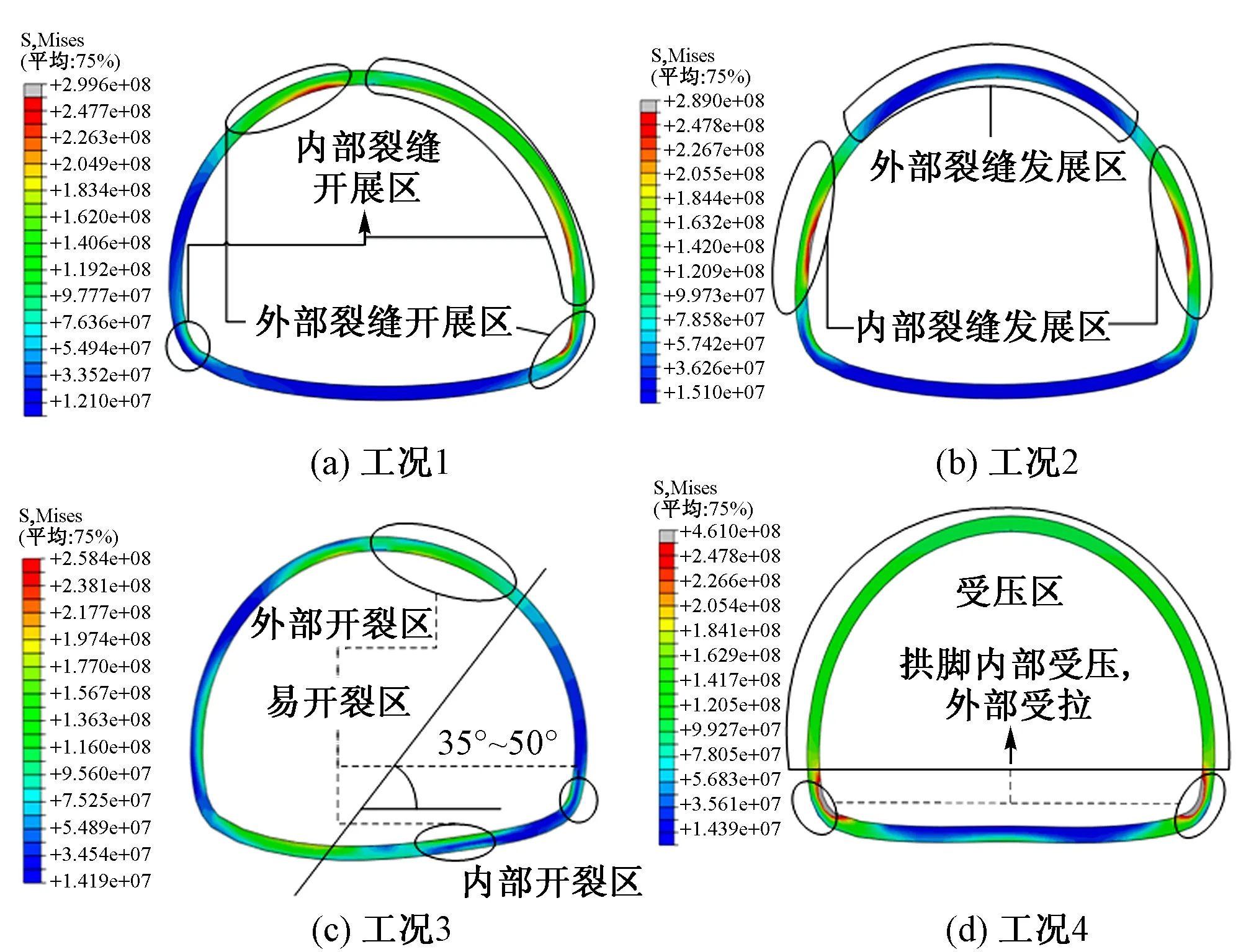
图5 隧道受力状态(单位:Pa)
图5是4种受不同区域围岩冻胀影响下衬砌的裂缝开展情况,其在偏冻区的衬砌正中处表现为内部受拉,在受冻边缘区外部受拉,内部受压,同时衬砌进入塑性区,微裂缝开展最明显。对拱顶的既有裂缝的后期开展,工况2和工况3影响最明显,在拱腰处,工况1和工况4最明显。衬砌的受拉状态会造成既有裂缝出现应力集中现象,还会导致裂缝两侧衬砌失效,失效半径为(8~20)d(d为衬砌厚度),由裂缝尖端到衬砌外部边缘均匀过渡。当衬砌厚度不足时,在局部冻胀情况下隧道结构将不稳定,安全系数降低。根据工况4可知,在隧道全部冻胀情况下,拱脚的应力状态远远超过材料的屈服强度,所以在高寒地区含水率较高的破碎围岩中修建隧道时,拱脚需要加强设计,防止冰冻损害。
隧道收敛位移沿纵向变化见图6。对非等埋深隧道,围岩冻胀导致衬砌侧向变形明显增大,当形成拱效应时,拱脚位移可以忽略不计,此时的应力是最大的,处于不稳定状态。偏冻荷载情况下(工况1、工况3),刚度中心偏向大曲率拱侧,直到和围岩一同形成等效拱,结构才处于稳定。局部冻胀导致大曲率拱内外侧的应力均比较大,但是两侧衬砌是处于受压状态,径向变形和轴向变形都比较小。工况2和工况4衬砌的变形出现马鞍状,整个衬砌应力和应变的标准差也都比较小,是最合理的受力结构形式。
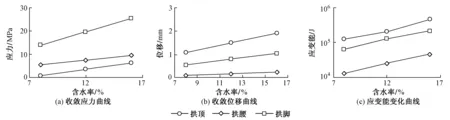
图7 应力、位移、应变能与含水率的关系曲线
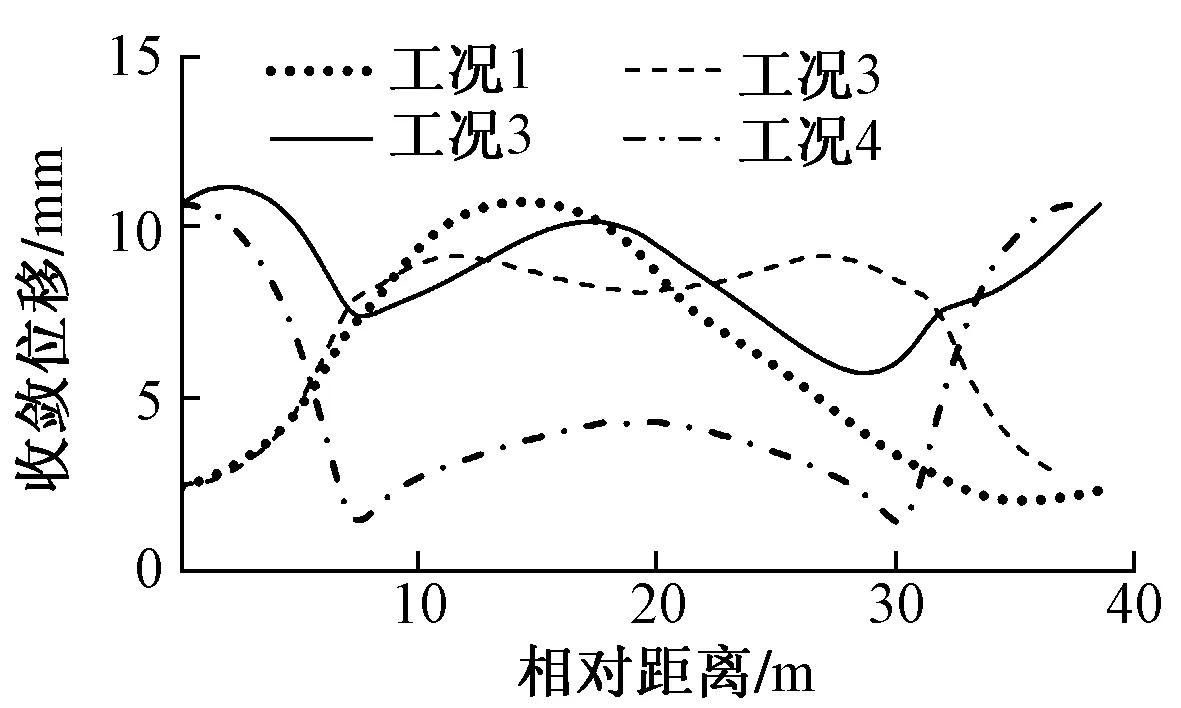
图6 隧道收敛位移沿纵向变化
3.3 含水率
若不考虑围岩裂隙间的冻缩影响,岩体的含水率不同,岩体的裂隙间的水分布就不一样,在有承压水的情况下,温度降到-4 ℃时水的膨胀体积将完全转化为膨胀力而作用的围岩上。但当岩体裂隙间的水处于不饱和状态、温度由0 ℃逐渐降低到-4 ℃时,靠近岩体裂隙壁的水先结冰,周围自由水填补岩体空隙,当空隙被填满时才表现出岩体的冻胀力。冻胀率计算式为
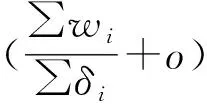
(15)
式中:wi为岩体流动水体积;δi为岩体裂隙体积;λ为水在-4 ℃时的膨胀系数;o为岩块自由水体积。
由于岩体处于冻胀状态,空隙已被水填满,所以岩体的名义弹性模量将会提高,且围岩类别越高弹性模量提高幅度越大。在此认为,Ⅴ级围岩经冻结后其材料力学特性可以达到Ⅱ级围岩。
将含水率影响引入到结构分析中,得到应力、位移、应变能与含水率的关系曲线,见图7。可知在岩体裂隙间水体达到饱和以前,冻胀温度一定时,围岩和衬砌的应力随着含水率的增大而增大。对于岩石隧道和高密实度围岩隧道,应力增长基本和含水率成正比例关系,比例系数由下到上依次递减,呈非线性关系。应力越集中的地方影响越大故拱脚的比例系数最大曲线最陡。变形同样随着含水率的增大而增大(图7(b)),但是和图7(a)并不成比例关系,主要原因为在冻胀和裂缝的双重影响下,使得衬砌的一些区域混凝土进入塑性区,同时因钢筋的影响,衬砌处于复杂应力状态,甚至出现塑性流动现象,即变形较大,应力相对较小。拱腰受影响很小,这主要是受隧道形状和围岩应力的控制,当这二者影响较大时,含水率将结构效应和荷载效应放大。分析图7(b)和图7(c),应变和含水率呈线性特征,而应变能曲线表现出明显的非线性特征,通过统计计算发现,其基本呈平方关系,变形越大平方系数越大。应变能是一个相对较敏感指数,当其达到一定程度时,应变能就会向周围传递,通过能量扩散保证结构稳定性,其扩散方式主要有结构变形、结构破坏、材料破碎。图7(c)明显表现出围岩含水率的影响很大。所以高寒地区隧道结构中的水不仅影响结构的寿命和使用安全性,更加影响结构的稳定性和安全性。
3.4 裂缝深度
扩展有限元法将裂缝端的单元软化,没有理论上的应力无穷大。通过间接的研究单元节点、分析裂缝应力状态来研究裂缝尖端处的应力。为获得拱顶裂缝初始深度不同、冻胀区域不同等工况下的裂缝扩展规律,计算模型采用了荷载-结构模型。
不同裂缝深度衬砌应力与收敛位移的关系见图8。可见,随着衬砌收敛位移的增加,裂缝处的应力是逐渐的增大的,并和收敛位移呈二次方关系,裂缝越深关系越明显。位移在0~0.6 mm之间应力会出现反向增大,5 cm裂缝的应力最大,15 cm裂缝的应力最小。在裂缝较大时,裂缝处衬砌可作为收敛位移增长的缓冲区,所以当变形较小时裂缝越深应力越小;随着位移的增大应力开始在裂缝处集中,裂缝越深应力集中速度越快,幅值也越大。
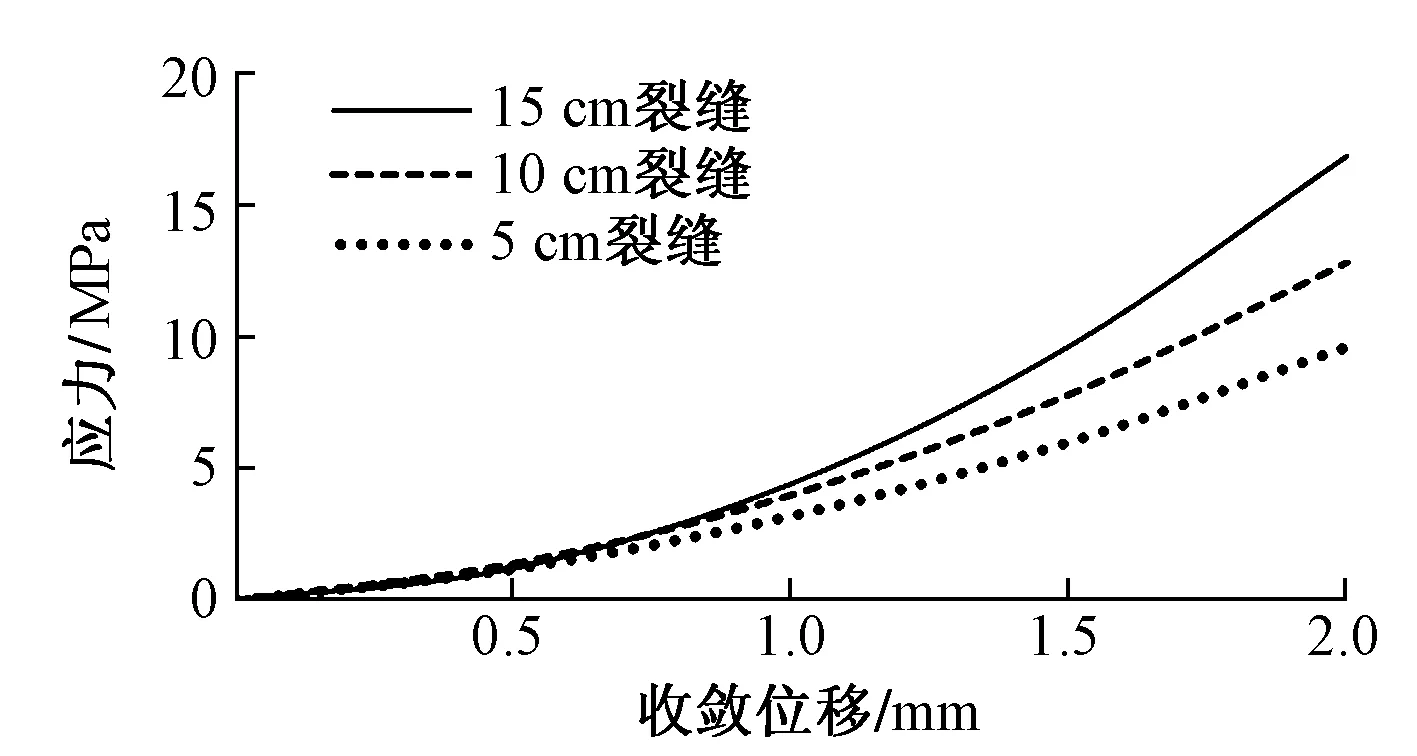
图8 不同裂缝深度衬砌应力与收敛位移的关系
分析裂缝两侧的4个点A,B,a,b(见图9),各点应力与开裂深度关系见图10。随着裂缝的开展裂缝单元节点应力越来越小,越靠近裂缝尖端线性关系越明显,反之则呈现非线性关系。由图10中a点可看出,裂缝出现并开展后,应力下降呈现先加快后平缓的趋势,主要是裂缝开展使得其两侧的材料失效,应力主要是旁边单元传递而来。裂缝的危害不仅使得衬砌加快开裂,更重要是使得衬砌的有效厚度减小。当厚度不足时衬砌将产生偏心距,有效厚度越小偏心矩越大。由于衬砌是轴心受力构件,当偏心距太大时将不可忽略,衬砌不再是单向受力而产生附加弯矩。附加弯矩会加速裂缝开展,甚至使得非裂缝区的衬砌超过材料屈服强度,整个衬砌处于超负载状态,安全系数减小。因此,在裂缝开展的初期进行养护十分重要。
4 实例计算分析
将弹性冻胀力引入到隧道结构计算中,理论分析中水在-4 ℃的膨胀率取9%,岩石的重度取19 kN/m3,埋深15 m,冻结深度为5 m,隧道半径取10 m,衬砌计算半径取10.60 m,围岩计算半径取15.60 m,岩石的孔隙率取0.25。将理论分析和数值分析应力予以对比,见图11,可知二者的分析结果基本一致。随着裂缝深度的增加,裂缝和非裂缝段衬砌的应力都呈递增关系。由于应力计算点在衬砌内边缘,所以和裂缝呈非线性关系。在计算中参考了JTG D70—2004,理论分析略比有限元计算大,算例采用的隧道模型是标准的圆形,所以拱脚的应力比拱顶大。
5 结论
本文通过对高寒地区中已有裂缝隧道的冻胀问题进行数值分析和理论分析,考虑了裂缝深度、围岩含水率、冻胀半径和非均匀冻胀因素。主要结论如下:
1)将围岩视为均匀弹性体,建立了已有裂缝隧道的冻胀弹性理论。并以张家口一高含水率铁路隧道为例,通过数值分析和理论分析的对比,弹性理论计算法可以得出较精确的衬砌应力状态和稳定性能,为高寒地区的隧道设计提供参考。
2)冻胀半径越大,衬砌应力越大,裂缝开展越长。当冻胀岩体的相对变形达到一定范围时,围岩原有裂隙和破碎程度都将增大,围岩承载力下降,再次受冻时冻胀力将增大。经过数个冻融周期后冻胀力将趋于稳定。
3)局部冻胀情况下,冻胀区域内衬砌正中部分内部受拉,受冻边缘区外部受拉,衬砌处于塑性状态,易出现微裂缝,隧道结构安全系数降低。在隧道全部受冻胀情况下,拱脚的应力状态远远超过材料的屈服强度,故在高寒地区修建隧道时,拱脚应加强设计,防止破坏。
4)受冻胀后围岩和衬砌的应力应变增长基本和含水率成正比关系。应力越集中的地方含水率影响越大,并且含水率具有对冻胀和裂缝的双重放大效应。
5)在冻胀力作用下,裂缝处的应力状态随着衬砌收敛位移的增大而逐渐增大,并与收敛位移呈二次方关系;随着裂缝的开展,裂缝单元的节点应力越来越小,越靠近裂缝尖端线性关系越明显,反之呈现非线性关系;受拉状态使得裂缝两侧衬砌失效,失效半径为衬砌厚度的8~20倍,衬砌有效厚度越小,偏心矩越大。
[1]谭贤君,陈卫忠,伍国军,等.低温冻融条件下岩体温度-渗流-应力-损伤(THMD)耦合模型研究及其在寒区隧道中的应用[J].岩石力学与工程学报,2013,32(2):239-250.
[2]陈中秋,张列.寒区冻融环境下隧道衬砌结构耐久性分析[J].公路,2013(9):272-275.
[3]苑郁林,赖远明.寒区隧道围岩冻融冻结环境识别和类别划分研究[J].现代隧道技术,2016,53(3):19-25.
[4]董长松,张晓旭,张弛,等.多年冻土区隧道衬砌混凝土冻融循环试验研究[J].公路,2015(11):244-247.
[5]刘泉声,康永水,刘滨,等.裂隙岩体水-冰相变及低温温度场-渗流场-应力场耦合研究[J].岩石力学与工程学报,2011,30(11):2181-2188.
[6]刘明,章青,刘仲秋,等.考虑渗透系数变化的地下结构温度-渗流耦合分析[J].力学季刊,2011,32(2):183-188.
[7]黄华南,吴亚平,刘运明,等.寒区隧道衬砌结构可靠性分析[J].铁道标准设计,2017,58(7):136-140.
[8]谭贤君,余祥宏,陈卫忠,等.岩土介质在冻融过程中的温度场研究及工程应用[J].岩石力学与工程学报,2012,31(增1):2867-2874.
[9]伍毅敏,李文博,傅鹤林,等.季冻区隧道过渡段二衬短周期冻融数值模拟[J].岩土工程学报,2017(10):1-6.
[10]叶飞,何川,夏永旭.公路隧道衬砌裂缝的跟踪监测与分析研究[J].土木工程学报,2010(7):97-104.
[11]王华牢,刘学增,李宁,等.纵向裂缝隧道衬砌结构的安全评价与加固研究[J].岩石力学与工程学报,2010,29(增1):2651-2656.
[12]尹蓉蓉,朱合华.氯盐和冻融循环复合作用对浅埋公路隧道安全性能的影响[J].四川建筑科学研究,2011,37(6):535-539.
[13]刘学增,张鹏,周敏.纵向裂缝对隧道衬砌承载力的影分析[J].岩石力学与工程学报,2012,31(10):2096-2102.
[14]徐颖,陈建平,左昌群.武当群片岩隧道剪切型纵向裂缝破坏机理[J].中南大学学报(自然科学版),2013,44(7):2950-2957.
[15]黄宏伟,刘德军,薛亚东,等.基于扩展有限元的隧道砌裂缝开裂数值分析[J].岩土工程学报,2013,35(2):266-275.
[16]张素磊,陈淮,王亚琼.基于灰色突变理论的隧道衬砌裂缝诊断模型[J].交通运输工程学报,2015(3):34-40.
[17]薛晓辉,张军,宿钟鸣,等.带裂缝隧道衬砌安全性评价及处治技术研究[J].重庆交通大学学报(自然科学版),2016,35(1):28-32.
[18]KRYVYI O F.Mutual Influence of an Interface Tunnel Crack and An Interface Tunnel Inclusion in a Piecewise Homogeneous Anisotropic Space[J].Journal of Mathematical Sciences,2015,208(4):409-416.
[19]SHEN B,ZHANG W Y,QI D P,et al.Wireless Multimedia Sensor Network Based Subway Tunnel Crack Detection Method[J].International Journal of Distributed Sensor Networks,2015,2015(2):1-10.

