结构设计参数对大跨度叠合梁斜拉桥稳定性的影响
邹建波,赵人达,许智强
(西南交通大学 土木工程学院,四川 成都 610031)
桥梁结构的稳定性是关系桥梁安全的主要问题之一,它与强度有同等重要的意义[1]。随着桥梁跨径的不断增大,桥塔高耸化、箱梁薄壁化以及高强材料的应用,结构整体和局部的刚度下降,使得稳定问题显得比以往更为突出[2]。桥梁结构特别是大跨度桥梁结构的稳定性不仅在成桥阶段,而且在分段施工中各个阶段同样是非常重要的,历史上有过许多因桥梁结构失稳而造成的灾难性事故。国内外曾经有不少桥梁,由于稳定计算不当或稳定性储备不够,发生失稳而导致全桥塌坍。
近年来,国内外学者对斜拉桥的稳定性做了大量的研究[3-5],其中包括非线性稳定和线性稳定。雷宇等[6]以重庆江津观音岩长江大桥为背景研究了斜拉索断裂,组合梁交界面相对滑移,桥面剪力滞效应等对极限承载力的影响。赵雷等[7]以鄂东长江大桥为背景研究了钢混结合部位置、索梁锚固方式、施工临时荷载、横向风荷载等对结构稳定性的影响。杨兴旺等[8]以南京上元门长江大桥为背景研究了风荷载、钢桁梁、活载布载方式和稳定性的关系。卜一之等[9]以苏通长江大桥为背景研究了破断拉索拆除时机、斜拉索承载能力、混凝土开裂及钢筋作用、横桥向风荷载、纵向约束等与稳定性的关系。从上述研究可以发现,国内外学者研究了诸多因素对大跨度斜拉桥稳定性的影响,但这些因素主要集中在外界因素,从结构设计参数本身出发的研究分析较少。
本文以西固黄河大桥主桥(177+360+177)m叠合梁斜拉桥为研究对象,其主梁截面形式为双工字形叠合梁。在考虑几何非线性、材料非线性、施工过程结构体系转换、变形和内力累加效应的影响下,分析西固黄河大桥主桥在成桥工况的非线性稳定性,研究斜拉索初始缺陷、桥塔材料、主梁材料等结构设计参数对大跨度斜拉桥稳定性的影响,从提高稳定性能的角度对大跨度斜拉桥的设计提出优化。
1 计算理论及方法
桥梁结构非线性稳定的实质即为结构极限承载力问题。其失稳破坏通常表现出大位移、小应变以及塑性屈服等特征,因此在有限元分析过程中应考虑结构几何与材料非线性的影响,即按双重非线性理论分析大跨度桥梁结构从初始加载直至达到其极限承载力这一过程的失稳破坏。双重非线性分析通常采用增量法,理论采用U.L列式法建立增量形式的平衡方程。
双重非线性稳定分析的基本方程为
([K0]+[Kσ]+[KL]){δ}={P}
(1)
式中:[Kσ]为小位移弹塑性刚度矩阵;[K0]为单元的初应力刚度矩阵即几何刚度矩阵;[KL]为大位移弹塑性刚度矩阵;δ为位移列阵;P为荷载列阵。
在U.L法的增量形式下,加载时把结构的临界荷载{P}cr分成荷载增量{ΔP}i(i=1,2,…,n),即
ΔP}i
(2)
对于任何一级荷载增量而言,荷载-位移曲线中的相应部分可以近似地认为是直线。在每个增量步对应的线性过程中计入该过程开始时的全部轴向力影响和应力-应变关系,这种等效线性化处理的结果也能相当好地逼近原来的非线性过程。增量形式的平衡方程为
[K]i-1{Δδ}i={ΔP}i
(3)
式中:[K]i-1是第i-1次加载{ΔP}i-1结束时的结构刚度矩阵,可在第i次加载前事先求出,其计算式为
[K]i-1=[K]0(i-1)+[K]σ(i-1)
(4)
第i级荷载增量作用结束时,结构承受的总荷载和总位移为
(5)
式中,{P}0和{δ}0为初始荷载列阵和初始位移列阵。
可见,这种方法可以监测结构加载达到临界荷载{P}cr过程中的荷载-位移变化以及结构内力行为。
失稳的临界荷载一旦确定,则相应的总变形{δ}cr所描述的变形曲线即为相应的失稳模态。
结构稳定安全系数K定义为
K=Pcr/PT
(6)
式中:Pcr为结构的极限承载力;PT为加载的荷载基数即某种工况下结构的设计荷载。
实际上,K为结构达到极限承载力时关于PT的加载倍数。本文考虑几何与材料双重非线性,其第二类稳定性的极限加载求解流程如图1所示。
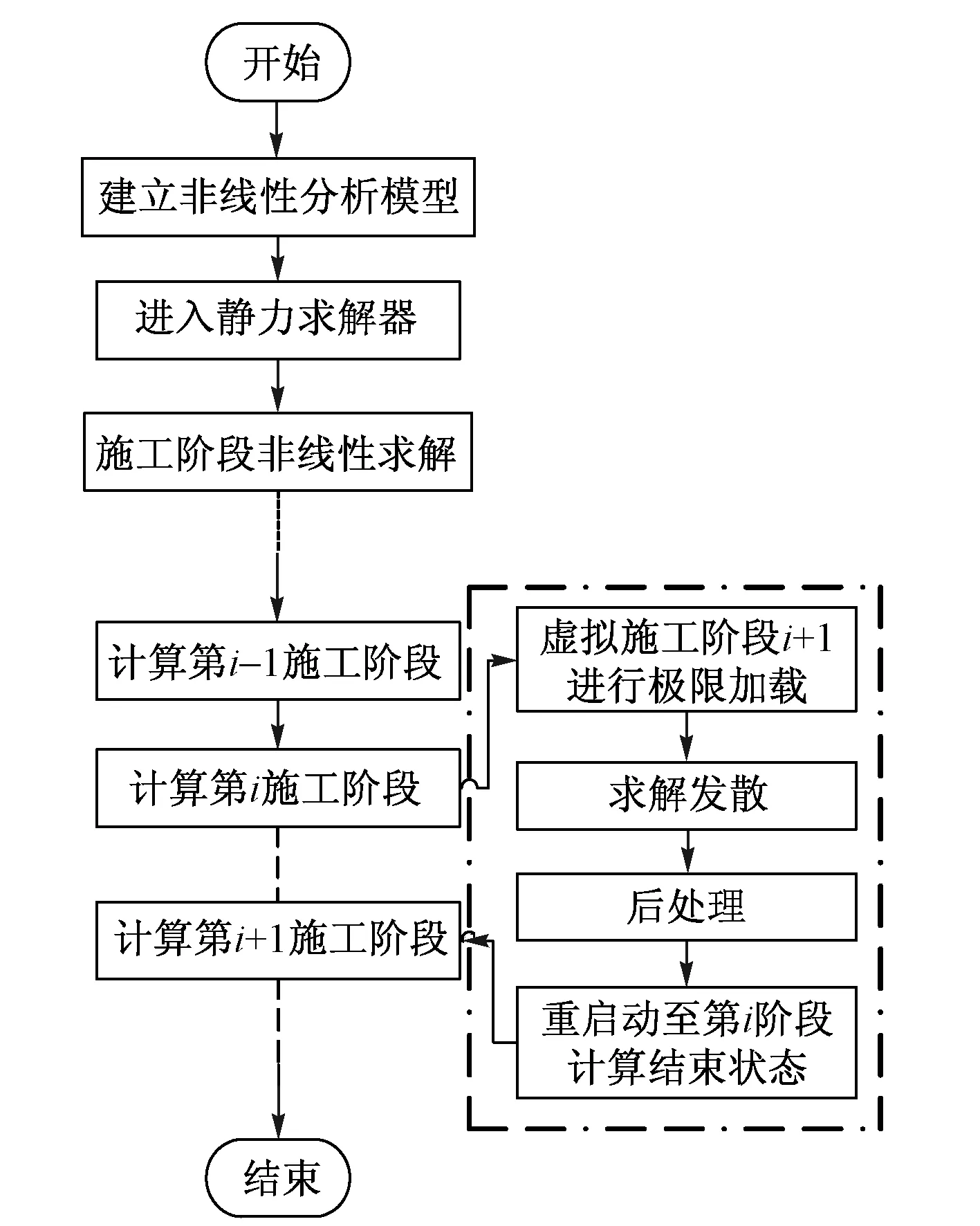
图1 加载求解流程
2 工程概况及有限元模型
2.1 工程概况
西固黄河大桥位于甘肃省兰州市西固区,跨越黄河、兰新铁路和西新路,为双塔双索面工字钢-混凝土叠合梁高速公路特大桥,车辆荷载等级为公路-Ⅰ级,设计车速70 km/h,设计基准期100年。主桥采用双塔三跨半漂浮体系叠合梁斜拉桥,跨径为(177+360+177)m,左右边跨各设置一个辅助墩和一个过渡墩,桥塔高均为151 m。桥塔采用C50混凝土,主梁采用Q370qD工字钢叠合C55混凝土板构成。全桥共布置56对(双索面共112根)斜拉索,斜拉索采用镀锌低松弛平行钢丝束,其标准抗拉强度为σb=1 860 MPa。图2给出了西固黄河大桥总体布置图。
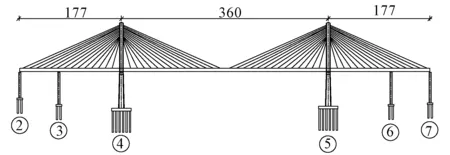
图2 西固黄河大桥立面(单位:m)
2.2 有限元数值模拟
计算采用有限元软件ANSYS建立全桥空间有限元模型。桥塔、桥墩及主梁采用Beam 188空间梁单元模拟,斜拉索采用Link 10杆单元模拟,其单元实常数为公称截面积与拉索初应变。主梁采用工字钢-混凝土叠合梁,在利用ANSYS建模时按照组合截面考虑,截面对应组成部分赋予相应的材料属性及其本构关系。主梁采用单主梁鱼骨式模型模拟,全桥划分各类单元463个,其中空间梁单元351个,空间杆单元112个。
关于计算过程中的双重非线性效应,其中几何非线性考虑了结构大变形效应、斜拉索垂度效应、弯矩轴向力耦合效应以及斜拉索破断应力的影响。结构大变形效应可在ANSYS非线性求解设置中开启,斜拉索垂度效应通过Ernst公式对其弹性模量进行修正:
(7)
式中:E为高强钢绞线的初始弹性模量;γ为斜拉索的材料重度;L为每根斜拉索的水平投影长度;σ为每根斜拉索的应力,有σ=T/A,其中T为斜拉索的设计索力,A为其公称截面积。将拉索应力除以等效后的拉索弹性模量即可得对应的拉索初应变,作为实常数赋予Link 10单元即可。
材料非线性采用MISES屈服准则[10],即
σe-σs=0
(8)
式中:σe为等效应力;σs为屈服应力。
σe计算式如下
(9)
式中:σx,σy,σz,τxy,τxz,τyz为对应的正应力与切应力分量。
2.3 边界约束条件
本桥在建立计算模型时,对于成桥工况,塔梁耦合3个平动自由度。模型详细的边界约束条件见表1。其中,x为顺桥向线位移;y为竖直方向线位移;z为横桥向线位移;rot-x为x向角位移;rot-y为y向角位移;rot-z为z向角位移;0表示无约束或不耦合自由度;1表 示有约束或耦合自由度。
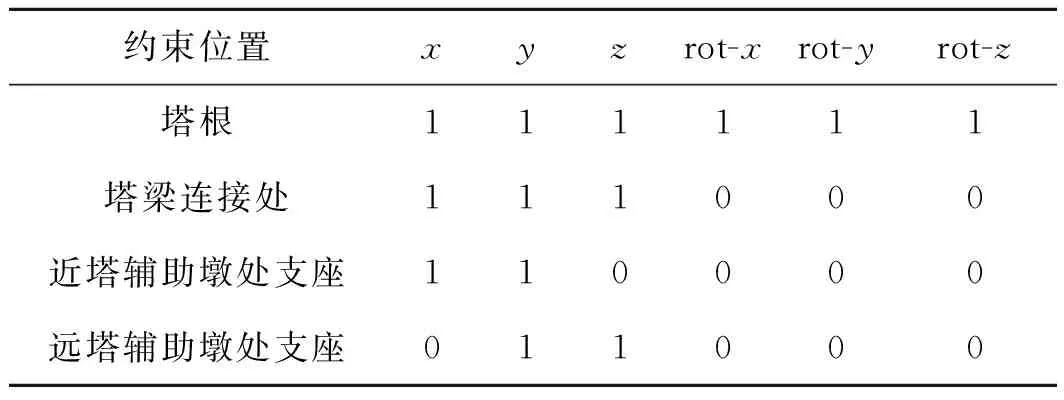
表1 成桥工况模型边界约束条件
2.4 计算工况及荷载
本文选取成桥工况进行结构设计参数分析,成桥工况荷载包括自重、二期恒载及横桥向静风荷载。除斜拉桥索力加载到设计张拉力外,其余荷载均按同一比例增量加载,直至结构达到其极限承载力为止[11]。
3 结构设计参数对稳定性的影响
3.1 斜拉索初始缺陷
斜拉桥在施工过程中不可避免地具有残余应力等初始缺陷[12-13],属于第二类稳定问题。本文考虑1%,5%,10% 3种斜拉索初始缺陷的情况,分别计算在成桥工况下对大跨度叠合梁斜拉桥稳定的影响,如图3所示。
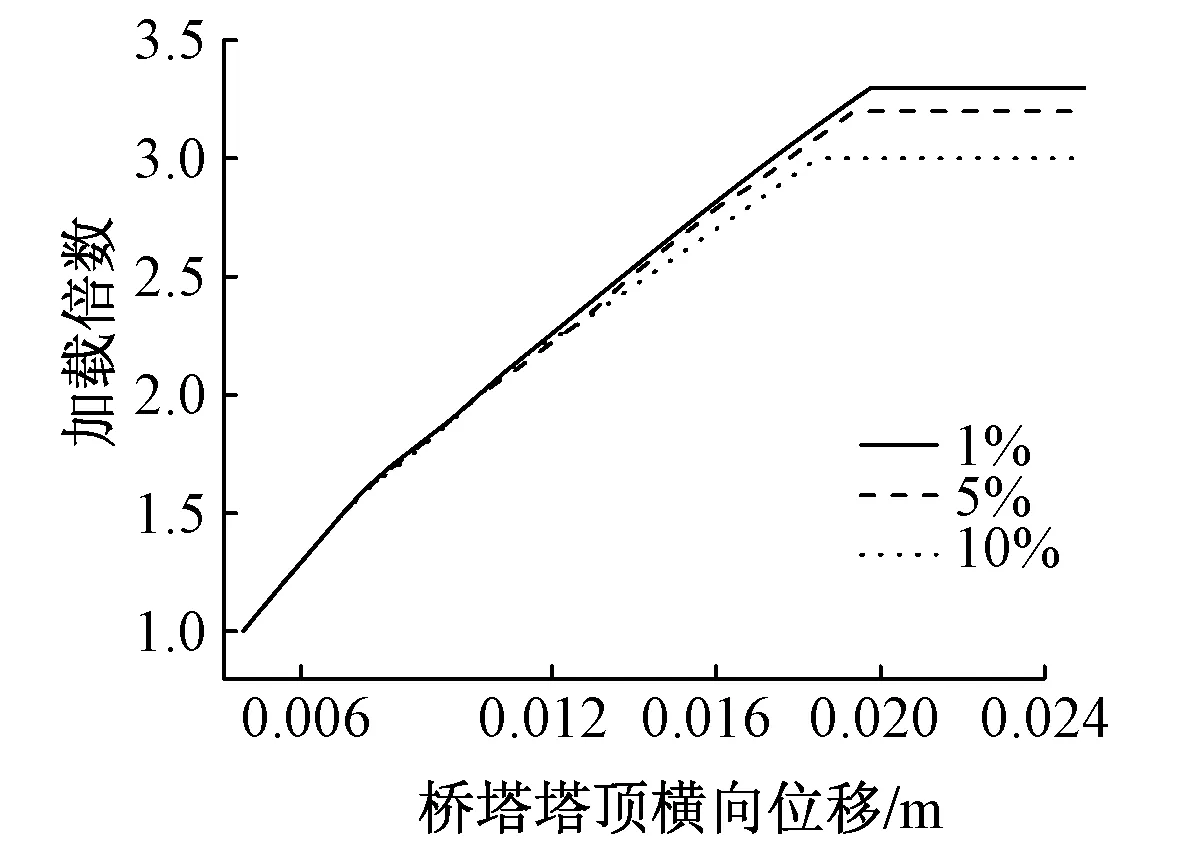
图3 成桥工况下不同初始缺陷塔顶荷载-位移曲线
由图3可知,斜拉索分别考虑1%,5%,10%初始缺陷时,在成桥工况的非线性稳定系数分别对应为3.3,3.2,3.0,下降了9.1%。荷载 - 位移曲线在荷载倍数小于2.0时,变化规律基本一致,在荷载倍数大于2.0后,初始缺陷越大,位移越大。
3.2 桥塔材料强度
混凝土材料按分段线性化折线本构模型处理[13]。其上升段的曲线简化成2条折线,σ0为轴心抗压强度,σc取40%轴心抗压强度。Ec为弹性模量,E0=(σ0-σc)/(ε0-εc),εu为极限压应变,如图4(a)所示。
桥塔混凝土分别采用C40,C50,C60 3种不同的强度等级,分别计算主桥在桥塔采用不同强度混凝土下的极限承载力,3种情况下的塔顶荷载 - 位移曲线如图4(b)所示。由图4(b)可知,桥塔混凝土分别采用C40,C50,C60,在成桥工况的非线性稳定系数分别对应为2.7,2.9,3.3,提高22.2%,提升较为明显,同一加载倍数下,混凝土强度越大,位移越小。
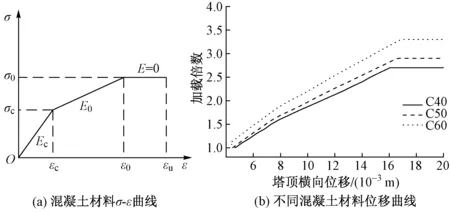
图4 桥塔混凝土材料σ-ε曲线及塔顶位移
3.3 主梁材料强度
钢材料按理想弹塑性本构模型处理。Eg为弹性模量,σs为屈服应力,钢梁材料σ-ε曲线如图5(a)所示。
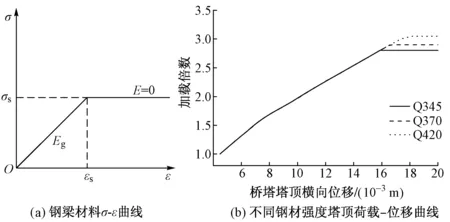
图5 主梁钢结构用材料σ-ε曲线及塔顶位移
主梁钢结构材料分别采用Q345,Q370,Q420 3种不同的强度等级,计算主桥在主梁采用不同强度钢材下的极限承载力,塔顶荷载 - 位移曲线如图5(b)所示。由图5(b)可知,当桥塔采用Q345,Q370,Q420钢材时,在成桥工况的非线性稳定系数分别对应为2.8,2.9,3.05,提高了8.9%,位移随着荷载倍数增加的变化规律基本一致。
4 结论
通过计算分析斜拉桥结构设计参数包括斜拉索初始缺陷、钢主梁强度、混凝土桥塔强度,在成桥工况对斜拉桥非线性稳定性的影响,得出以下结论:
1)当斜拉索分别考虑1%,5%,10%初始缺陷时,在成桥工况的非线性稳定系数分别对应为3.3,3.2,3.0,下降了9.1%,影响较大。
2)桥塔混凝土分别采用C40,C50,C60时,在成桥工况的非线性稳定系数分别对应为2.7,2.9,3.3,提高了22.2%,提升较为明显,同一加载倍数下,混凝土强度越大,位移越小。
3)当主梁采用Q345,Q370,Q420钢材时,在成桥工况的非线性稳定系数分别对应为2.8,2.9,3.05,提高了8.9%。位移随着荷载倍数增加的变化规律基本一致。
[1]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1996.
[2]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2015.
[3]张敏,高宗余,陈佳,等.千米跨度公铁两用钢桁梁斜拉桥几何非线性研究[J].桥梁建设,2014,44(5):15-20.
[4]HONG J K,DEOK H W,YOUNG J K,et al.Structural Stability of Cable-stayed Bridges During Construction[J].International Journal of Steel Structures,2017,17(2):443-469.
[5]XU M,GUO W W,XIA H,et al.Nonlinear Aerostatic Stability Analysis of Hutong Cable-stayed Rail-cum-road Bridge[J].Wind and Structures,2016,23(6):485-503.
[6]雷宇,赵雷,黎曦.大跨度组合梁斜拉桥极限承载力影响因素[J].西南交通大学学报,2009,44(6):812-816.
[7]赵雷,孙才志,杨兴旺.鄂东长江大桥施工过程非线性稳定性分析[J].西南交通大学学报,2012,47(5):741-747.
[8]杨兴旺,赵雷.大跨度三塔斜拉桥稳定性分析[J].四川建筑,2003(4):38-40.
[9]卜一之,赵雷,李乔.苏通长江大桥结构非线性稳定性研究[J].土木工程学报,2013,46(1):84-91.
[10]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.
[11]陈良江.我国铁路斜拉桥的实践与设计参数研究[J].铁道建筑,2017,57(10):1-6.
[12]赵雷,杨兴旺.南京长江二桥斜拉桥施工过程稳定性分析[J].公路交通科技,2005(7):78-81.
[13]赵雷,武芳文.南京长江三桥初步设计方案施工阶段稳定性分析[J].西南交通大学学报,2005,40(4):467-472.

