经验小波变换在桥梁模态参数识别中的应用
夏 雄,单德山
(西南交通大学 土木工程学院,四川 成都 610031)
桥梁模态参数识别在桥梁健康监测领域中有着重要意义,是桥梁结构进行损伤识别和状态评估的前提和基础。现有时域、频域模态参数识别方法有很多,但应用于桥梁上效果都不甚理想,时频域分析方法能够充分利用动力响应的时域和频域信息,获取不同时间和频率对应的能量密度、强度等信息。其中基于小波变换和HHT的模态参数识别方法得到广泛研究并取得了一定的成果。但小波变换的小波基选择困难,时、频分辨率无法兼顾,不具有自适应性;HHT中的经验模态分解(EMD)会因信号中参杂的噪声、间断和脉冲等造成模态混叠问题,使分解得到的本真模态函数(IMF)失去物理意义,此外端点效应、缺乏完备的理论基础、计算效率较低等问题都使得其进一步的研究成为困难。
2013年,文献[1]提出了一种新的信号处理方法即经验小波变换(EWT),该方法通过对原信号的傅里叶谱进行分割,在每个分割区间内构建小波基函数,实现对原信号的分解,提取固有模态。文献[2]针对染噪非平稳非线性信号提出了一种自适应多信号分类EWT方法,对此类信号进行了精确时频表示。文献[3]结合EWT和傅里叶基矩阵提出了一种精确频率估计的方法。文献[4]结合次序统计滤波器对强噪声、非平稳信号提出了一种改进的EWT方法。文献[5-10]基于EWT方法,对机械故障诊断领域进行了大量的研究。尽管经验小波变换在各领域取得了一些发展,但在桥梁结构模态参数识别上仍没有应用的先例,为从实测的非线性、非平稳桥梁动力测试信号中有效地识别出模态参数,本文引入EWT方法对测试信号进行处理,并以某曲线斜拉桥模型试验为基础,验证了所提方法的有效性。
1 经验小波变换
经验小波变换通过对原信号的傅里叶谱进行分割,在每个分割区间构造相应的带通滤波器,从原信号中提取出不同的调幅-调频成分。首先,将原信号的傅里叶谱归一化使得频率ω∈[0,π],假定将谱分割成N个连续的区间,每个区间表示为Λn=[ωn-1,ωn](其中n=1,2,…,N且ω0=0,ωN=π),以ωn为中心,设置宽度为2τn的过渡带,其中τn=γωn,γ为系数。
确定分割区间后,根据Meyer小波的构造方法,定义经验尺度函数和经验小波函数为
式中:
β(x)=x4(35-84x+70x2-20x3)
(3)
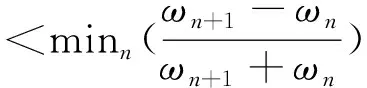
(4)
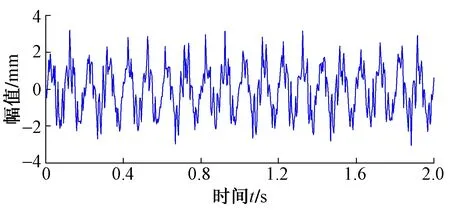
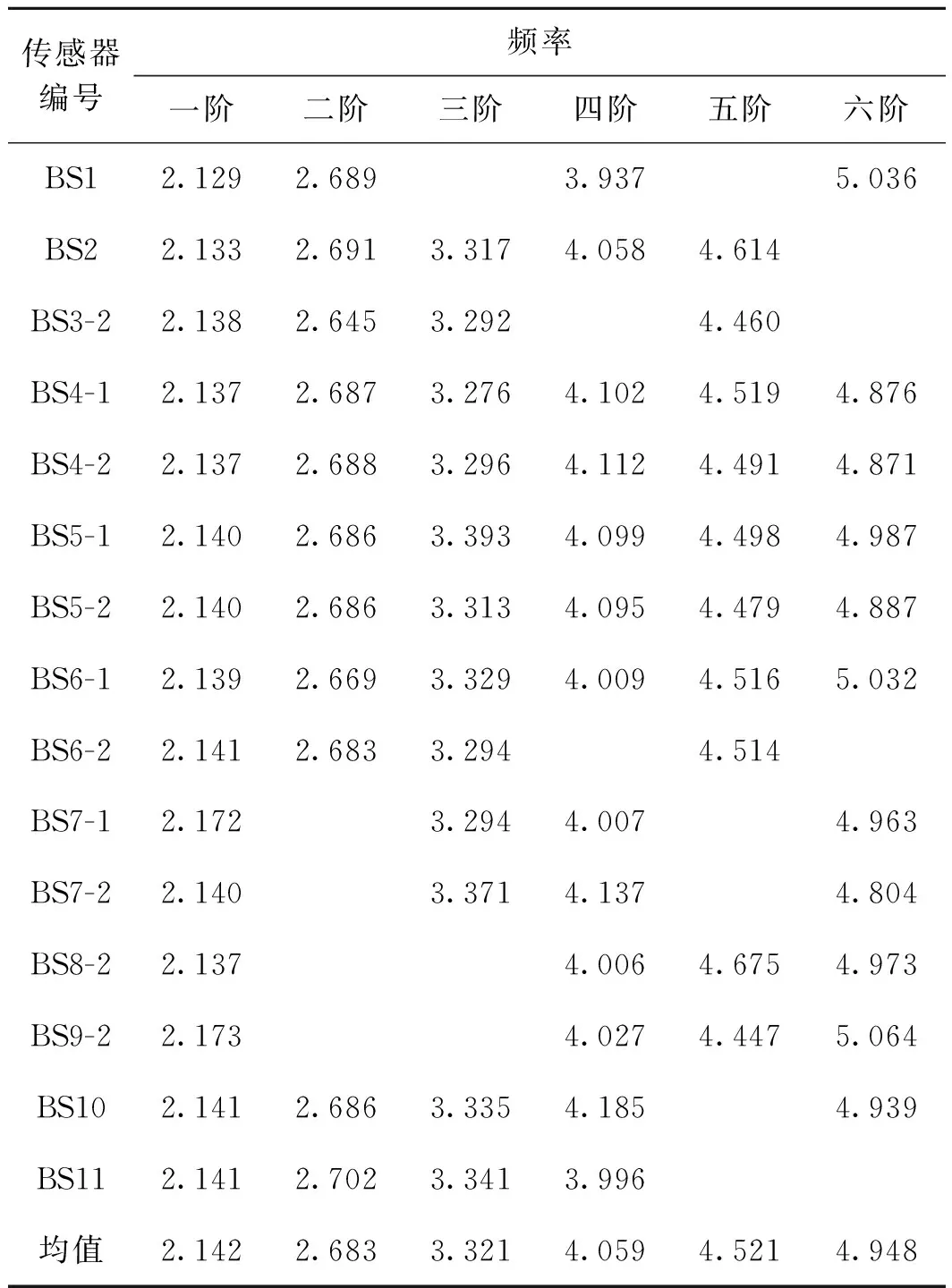
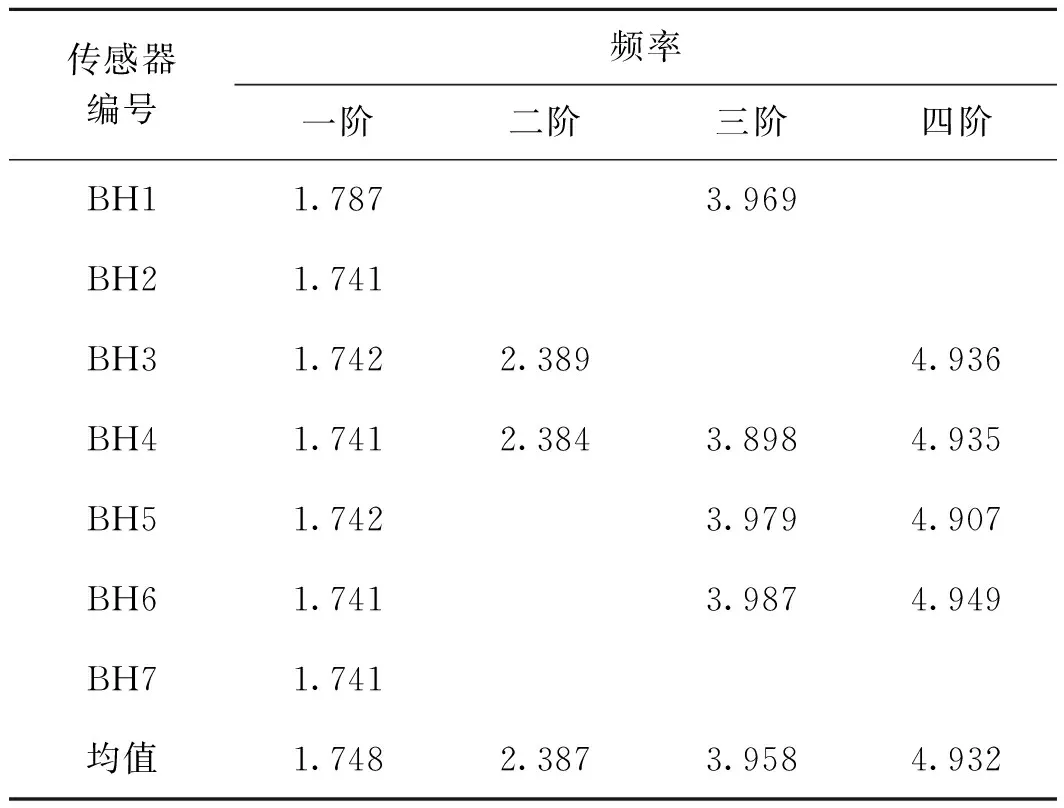
在EWT方法中,傅里叶谱的分割至关重要,它是该方法自适应性的体现。假设将频谱分割成N段,则除了0和π之外,还需要寻找N-1个边界。求出频谱函数中所有的局部极大值,假设有M个,若M (5) 根据传统小波变换的方法定义经验小波变换,细节系数和近似系数分别定义为 则分解得到的经验模态函数定义为 (0,t)*φ1(t) (8) (9) 式中:“*”表示卷积。 为验证EWT方法的有效性,对仿真信号x(t)进行分析处理,x(t)由10 Hz的正弦信号x1(t)、50 Hz的调幅信号x2(t)、基频为80 Hz及调制频率为40 Hz的调频信号x3(t)构成,并对合成信号添加25%的随机噪声,见式(10)。染噪合成信号时域波形图见图1,仿真信号的EWT处理结果见图2。 (10) 图1 信号x(t)的时域波形 图2 信号x(t)的EWT分解结果 由图2可见,EWT分解结果与原信号的3个分量一一对应,波形清晰,不存在模态混叠。将分解得到的IMF进行Hilbert变换,得到时频曲线见图 3。图3得到很好的分割,频率值清晰稳定。各IMF分量的频率平均值分别为9.97,48.41,79.98 Hz,与原信号各成分基频误差很小。可以得出:EWT根据信号的先验知识,能够提取出原信号中不同的调幅-调频成分,将含有固有特征的各个信号分量有效分离。 根据本文描述的EWT方法,基于MATLAB平台,编制了模态参数识别相关程序,并以某曲线斜拉桥模型试验为例,对动力实测数据进行处理,识别该模型桥的模态参数。 试验桥原型为一双塔双索面的公路曲线斜拉桥,全长545 m,曲率半径为550 m,模型桥缩尺比例为1∶20,全长27.17 m,桥跨布置形式为(2.41+4.05+14.25+4.05+2.41)m,见图 4。 图4 模型桥梁整体布置 模型桥塔为菱形,采用钢材制作;主梁设置1.987%的纵坡,采用Q235钢板制作;全桥共有120根斜拉索,采用碳素弹簧钢丝模拟。在桥梁主梁上布置加速度传感器,记录模型桥在环境激励下的动力响应。沿顺桥向共布置竖向传感器11处,其中两边跨各2处,中跨7处;横向传感器7处,其中两边跨各2处,中跨3处,试验现场见图 5。 图5 模型试验现场 采用前述EWT方法对试验测试数据进行分析,以跨中位置的竖向传感器BS5-2和横向传感器BH4为例,对测试信号进行分解,然后将各阶IMF进行Hilbert变换,得到瞬时频率见图 6。 图6 测试信号的EWT-Hilbert谱 对瞬时频率进行直线拟合并结合随机减量技术[11],识别出竖向前六阶频率值分别为2.140,2.686,3.313,4.095,4.479,4.887 Hz;横向前四阶频率值分别为1.741,2.384,3.898,4.935 Hz。为进一步验证计算结果的可靠性,计算测试信号的自功率谱见图7。 图7 测试信号自功率谱 图7(a)中竖向振动信号自功率谱中前6个峰值点频率分别为2.156,2.656,3.281,4.000,4.563,4.875 Hz。 图7(b)中横向振动信号自功率谱中前4个峰值点频率分别为1.750,2.375,4.031,4.875 Hz。 对比识别结果与自谱分析结果可知:采用EWT方法计算的频率值与自功率谱中的峰值点频率很接近,由于自功率谱峰值点频率值可对结构固有频率作近似估计,所以本文所用方法计算结果可靠。 采用该方法对其余传感器测试数据进行处理,模型桥各阶频率计算结果见表1、表2。 表1 竖向自振频率计算结果 Hz 表2 横向自振频率计算结果 Hz 针对桥梁结构模态密集、测试信号噪声强度高等特点,利用EWT方法在信号处理上的优势,将其运用到桥梁模态参数识别上,通过仿真信号验证了EWT方法对信号分解的有效性。结合某曲线斜拉桥模型试验测试数据,证明了本文所提方法的可行性,得到以下结论: 1)EWT方法能够很好地对测试信号进行分解,分解得到的各阶IMF相互正交,不存在模态混叠现象。 2)所提的方法能正确识别出桥梁模态参数,识别出模型桥梁前六阶竖向自振频率值分别为2.142,2.683,3.321,4.059,4.521,4.948 Hz,前四阶横向自振频率值分别为1.748,2.387,3.958,4.932 Hz,识别结果可信度高。 [1]GILLES J.Empirical Wavelet Transform[J].IEEE Transactions on Signal Processing,2013,61(16):3999-4010. [2]AMEZQUITA-SANCHEZ J P,ADELI H.A New Music-empirical Wavelet Transform Methodology for Time-frequency Analysis of Noisy Nonlinear and Non-stationary Signals[J].Digital Signal Processing,2015,45:55-68. [3]PRAKASH L,MOHAN N,KUMAR S S,et al.Accurate Frequency Estimation Method Based on Basis Approach and Empirical Wavelet Transform[C]//Proceedings of the Second International Conference on Computer and Communication Technologies.New Dephi,India:Springer,2015:801-809. [4]HU Y,LI F,LI H,et al.An Enhanced Empirical Wavelet Transform for Noisy and Non-stationary Signal Processing[J].Digital Signal Processing,2017,60:220-229. [5]JIANG Y,ZHU H,LI Z.A New Compound Faults Detection Method for Rolling Bearings Based on Empirical Wavelet Transform and Chaotic Oscillator[J].Chaos Solitons & Fractals,2016,89:8-19. [6]CHEN J,PAN J,LI Z,et al.Generator Bearing Fault Diagnosis for Wind Turbine via Empirical Wavelet Transform Using Measured Vibration Signals[J].Renewable Energy,2016,89:80-92. [7]CAO H,FAN F,ZHOU K,et al.Wheel-bearing Fault Diagnosis of Trains Using Empirical Wavelet Transform[J].Measurement,2016,82:439-449. [8]李志农,朱明,褚福磊,等.基于经验小波变换的机械故障诊断方法研究[J].仪器仪表学报,2014,35(11):2423-2432. [9]黄南天,张书鑫,蔡国伟,等.采用EWT和OCSVM的高压断路器机械故障诊断[J].仪器仪表学报,2015,36(12):2773-2781. [10]冯博,李辉,郑海起.基于经验小波变换的轴承故障诊断研究[J].轴承,2015(12):53-58. [11]单德山,李乔.桥梁结构模态参数的时频域识别[J].桥梁建设,2015(2):26-31.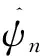
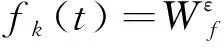
2 仿真信号分析
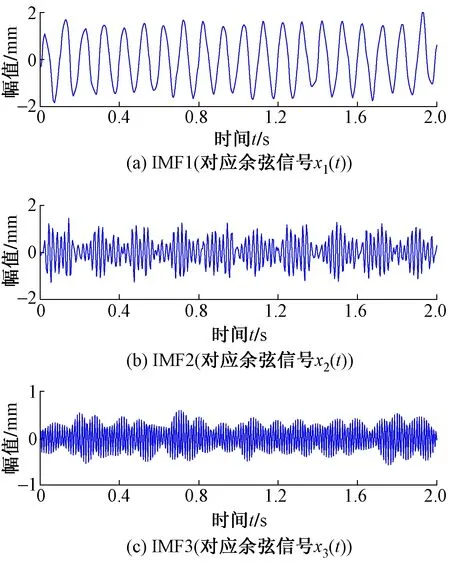
3 实测信号分析
3.1 试验概况
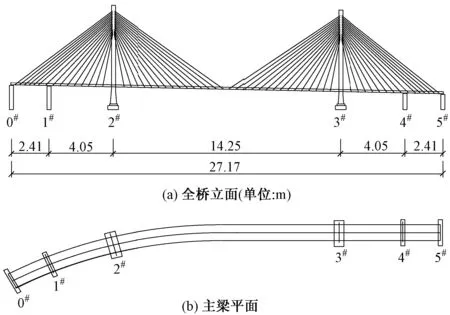

3.2 参数识别
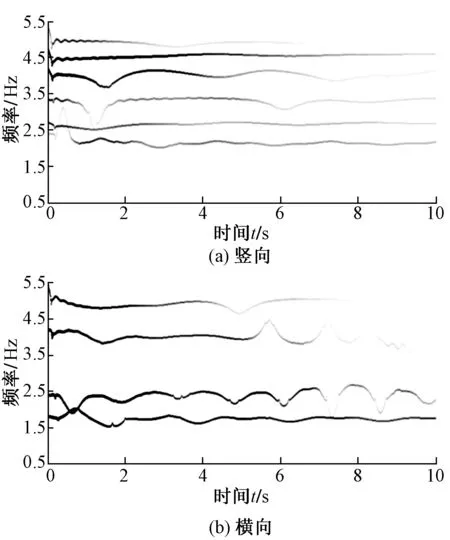
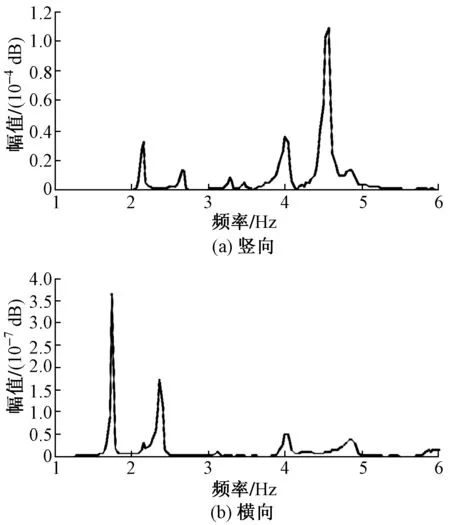
4 结论

