FSAE赛车双横臂式前悬架运动学仿真及优化

徐晶 李磊 单金良

扬州大学 机械工程学院 江苏省扬州市 225127

1 引言

悬架系统是汽车的重要部件，其设计好坏对车辆行驶平顺性、操纵稳定性和安全性有着重要的影响。在车辆悬架的设计及优化中，以多刚体动力学 ADAMS 软件为基础的悬架运动学分析成为了一种常用手段。 在FSAE赛车设计中，采用双横臂式独立前悬架，通过ADAMS/Car模块建立该悬架的虚拟样机模型，进行运动学仿真，并利用ADAMS/Insight进行优化仿真，最终获得优化结果，改善了悬架系统的性能，从而达到优化设计的目的。

2 双横臂式前悬架建模

根据赛车的悬架特性和性能要求，本文设计了双横臂式独立前悬架，综合确定其主要参数，运用CATIA软件对该前悬架进行三维设计，其参数化模型如下图1（a）所示。同时通过提取三维模型的主要硬点坐标值，修改悬架弹簧、减振器的相关参数，并确定主要部件的连接关系，建立了不等长双横臂前悬架的运动学模型，通过引入ADAMS /Car的标准悬架实验平台，最终完成了双横臂前悬架仿真模型，如下图1（b）所示。

3 前悬架运动学仿真

FSAE赛车前悬架具有多自由度的运动要求和非常严苛的空间及运动学约束条件，是非常典型的运动学优化目标对象。首先对其进行平行跳动仿真实验，步长为50，车轮跳动范围为±30mm，仿真结束后，通过ADAMS后处理模块，可以获得多种表征悬架性能的参数随车轮跳动而变化的曲线，结果如下：

（1）主销内倾角与后倾角变化规律

图2中前悬主销内倾角在车轮上下跳动30mm行程内，从11.1°变化到12.8°，变化了1.7°。前悬主销后倾角在车轮上下跳动30mm行程内，从1.051°变化到1.057°，变化了0.006°。上述两个角度均在合理变化范围内，不需要进一步优化。

（2）前轮外倾角和前束角变化规律：

图3中车轮外倾角变化范围是 -0.89°到0.81°，变化量为1.7°；车轮前束角变化范围是 -1°到1.27°，变化量为2.27°，这两角度的变化幅度较大。考虑到车轮跳动时外倾角的变化对车辆的稳态响应特性等有很大的影响，且为保持汽车直线行驶，所以外倾角和前束角均设计为负值。通过上述仿真分析，本文设计的悬架需要进行进一步的优化设计，以获得最佳性能。

图1 前悬架运动学仿真模型

4 前悬架多目标优化分析

Adams 软件的一个Insight子模块具有强大的实验设计功能，可以通过多因素设计，对复杂的悬架动力学问题进行非常便捷的流程化优化。通过对赛车前悬架的多因素设计变量的数量、水平以及特性进行分析，制定如下试验设计方案。

图2 主销内倾角和主销后倾角变化曲线

图3 前轮外倾角和前轮前束角变化曲线

（1）设定目标变量和设计变量：根据上述仿真分析结果，前悬外倾角和前束角设置为优化的目标变量，上下横臂的四个内点坐标变量对这两个参数变化有较大影响，选择其Y、Z坐标设置为八个设计变量，变化范围为-5～5mm。

（2）试验设计的运行：通过设置试验相关参数，运行之后得到设计变量对目标变量的影响程度，直观地反映了设计变量对目标变量影响重要性程度结果如下：

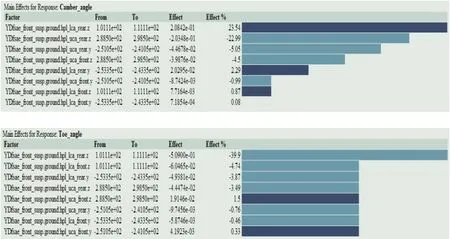
从上图中可以看出上横臂后点的Y、Z和下横臂前后点的Z等四个设计变量对前悬外倾角和前束角的影响显著。

（3）优化分析：利用Adams软件的Insight模块，建立标准的悬架优化模型，首先固定对目标变量影响不大的四个设计变量值，并设定其余显著设计变量的预期值和权重百分比，最后运行其结果如上表所示。

表1 前悬架优化设计结果

为验证优化结果的正确性，将优化后设计变量的值重新输入前悬架运动学仿真模型，重新仿真，并输出优化前后悬架运动学特性前轮外倾角和前悬前束角变化结果，其结果如下：

图5 优化前后前轮外倾角和前束角对比

图中实线为优化前曲线，虚线为优化后曲线，可以看出通过对前悬架进行多目标优化设计后，前轮外倾角和前束角两个参数在相同的车轮跳动行程内，其变化范围明显变小，进一步验证了优化模型的正确性，同时也改善了FSAE赛车的操控稳定性，提升了前悬的性能。

5 结语

本文在ADAMS/Car模块中建立了FSAE赛车双横臂独立悬架的运动学仿真模型，并对其进行了运动学仿真分析，利用 ADAMS/Insight 模块通过设定设计变量、综合目标函数和约束条件对前悬架进行了多目标优化设计。最终实例优化结果表明，通过适当修改悬架相关硬点坐标值，可使赛车悬架综合性能得到明显提高，并为FSAE 赛车整车悬架的设计、制造和调试提供了一定的参考作用。