基于并行计算的大数据挖掘技术及其在电站锅炉性能优化中的应用

刘炳含， 付忠广， 王永智， 王鹏凯， 高学伟

(华北电力大学 电站设备状态监测与控制教育部重点实验室，北京 102206)

随着信息数字化时代的迅速发展，电力行业信息化也得到快速发展。厂级监控信息系统(SIS，Supervisory Information System)和分布式控制系统(DCS，Distributed Control System)在电厂得到广泛应用，使得电厂海量运行数据得以保存，数据挖掘技术在电力行业迅速崛起，很多学者开始运用数据挖掘技术研究解决电站机组中遇到的问题[1-6]。数据挖掘聚类分析方法被广泛应用于解决电站锅炉效率和NOx排放等优化问题。赵欢等[7]提出一种基于模糊C-均值聚类算法实现多参量同步聚类，以确定锅炉监控参数基准值的方法。钱瑾等[8]利用K-means算法分析实时运行数据，挖掘出再热器压损和锅炉排烟温度的基准值。

聚类分析[9]作为数据挖掘中的经典分析算法已经被广泛应用于生物信息、网络、图像分析、智能推荐等许多领域。K-means(均值)[10]算法是一种经典的聚类算法，具有算法简单、收敛速度快等优点，在对数据进行挖掘聚类时得到广泛应用。但在实际运用中，K-means算法也存在不足之处，该算法依赖初始聚类数目，在聚类结果中容易出现局部最优解，随着迭代总次数的增加，聚类耗时增加。同时，面对海量数据聚类会产生大量候选集及冗余数据集，降低聚类效率及准确率。为此，笔者首先引入粗糙集属性约简方法和Canopy聚类算法对K-means算法进行改进，并利用粗糙集属性约简方法对源数据进行简化，剔除冗余数据；结合Canopy算法，利用其不需设定聚类数目的特点，对原始数据进行聚类分析，以确定初始聚类中心及聚类数目，再通过K-means算法进行迭代计算，得到最后的聚类结果，K-means算法的不足因此得到一定程度的弥补。

随着智能电网的建设与普及，电厂DCS控制系统中储存的发电数据量呈指数增加，使得传统的数据挖掘算法无法满足数据量、数据类型不断增多的需求，落后的数据分析处理能力与数据快速增长之间的矛盾突显。K-means算法在聚类过程中迭代总数增加，使得聚类效率降低、耗时增加，面对海量数据已经不能满足需求。寻求大数据分析挖掘的高级方法成为亟需解决的问题。

云计算的出现适应了这种海量数据挖掘需求，云计算技术通过建立集群将储存和计算能力分到集群中的多个储存和计算节点上，从而实现了对大数据集的储存和计算[11]。Hadoop是一个用于构建云平台的Apache开源项目，其核心构件是分布式文件系统(HDFS)和MapReduce，HDFS对大文件实现储存和容错，MapReduce编程模式实现并行计算[12]。将Hadoop与传统数据挖掘相结合的一个关键问题是传统数据挖掘算法并行化的实现，并行化计算是现阶段处理海量数据最有效的方法[13-16]。

面对电站机组海量、高维度数据，笔者引入粗糙集理论和Canopy算法对K-means算法进行改进，通过MapReduce编程模式对改进K-means算法实现并行化，以处理海量数据的计算，形成基于大数据技术的高效聚类算法，即RCK-means算法。与传统K-means算法相比，新算法避免了出现局部最优解，提高了聚类准确率，剔除了冗余数据集，并极大地提高了聚类效率。

1 相关工作背景

1.1 粗糙集理论

粗糙集理论是由波兰数学家Pawlak于1982年提出的一种处理不确定性和不精确性问题的数据分析理论，其以信息系统为主要研究对象，在保持信息系统中数据分类能力不变的前提下，通过知识约简确定问题的分类规则或决策[17]。与其他处理不确定问题的理论相比，粗糙集理论最显著的区别在于其不需提供问题所需处理的数据集合之外的任何先验知识，对其他理论有很强的互补性。目前，粗糙集理论在临床医疗诊断、预测与控制、模糊识别与分类等很多领域得到广泛应用[18]。

定义2设一个信息系统S=(U，A，V，f)，C∪D=A,C∩D=φ,若属性集A由条件属性集C和决策属性集D构成，则称S为一个决策信息系统。

定义3设一个信息系统S=(U，A，V，f)，∀R⊆A，论域U上关于R的不可分辨关系(等价关系)定义为：

(1)

定义4设一个信息系统S=(U，A，V，f)，∀X⊆U，R⊆A，则X基于等价关系IND(R)的上、下近似集分别定义为：

R*(X)={x∈U|[x]R∩X≠φ}

(2)

R*(X)={x∈U|[x]R⊆X}

(3)

集合PR=R*(X)称为X基于等价关系IND(R)的正域；集合NR(X)=U-R*(X)称为X基于等价关系IND(R)的负域；集合BR(X)=R*(X)-R*(X)称为X基于等价关系IND(R)的边界域。

当BR(X)≠φ，即R*(X)≠R*(X)时，则X为R的粗糙集。

定义5设P是论域U上的一个等价关系簇，R∈P，若IND(P-{R})≠IND(P)，则称R为P的必需，否则不必需。若等价关系簇P中的每一门知识在P中都是必需的，则称等价关系簇P是独立的，否则是相关的。

定义6设P是论域U上的一个等价关系簇，Q⊆P且Q≠φ,若IND(Q)=IND(P)且Q是独立的，则称Q为P的一个约简。而等价关系簇P的所有约简形成的子簇称为RED(P)，P中所有必需知识形成的子簇称为P的核，记为CORE(P)。

定义7设P和G为论域U上的2个等价关系簇，G的P正域定义为：

Pp(G)=PIND(P)(IND(G))

(4)

定义8设P和G为论域U上的2个等价关系簇，且R∈P，若PP(G)≠PP-(R)(G)，则称R为P中G相对必需的；否则称R为P中G相对可约的。如果每一个R∈P都是G相对必需的，则称P相对于G独立；否则，称P为G相关的。

定义9设P和G为论域U上的2个等价关系簇，若Q是P的G相对独立子簇，且PQ(G)=PP(G)，则称Q为P的一个G相对约简。

属性约简是粗糙集理论的核心内容，其从原始特征中进行最佳子集选择，在众多特征中选择最重要的特征，剔除冗余数据，降低数据维度，提高分析效率。笔者采用基于Pawlak属性重要度的决策表属性约简算法进行属性约简，属性约简的基本框架如图1[19]所示。

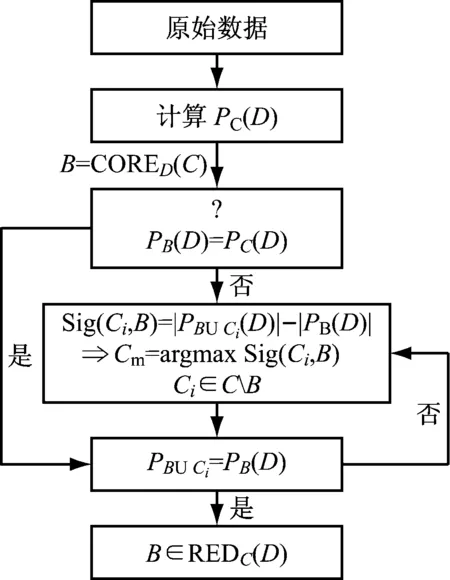
图1 属性约简的基本框架

1.2 Canopy算法

Canopy算法思想：对于海量数据，将输入的数据点使用距离测量方法划分为一些重叠的簇，称为Canopy，然后对处于Canopy中的点采用精度较高的计算方法进行聚类[20-21]。

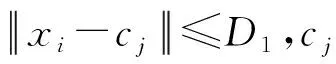
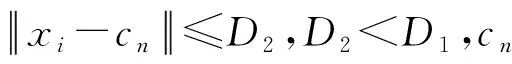
1.3 K-means算法

K-means算法[10]是一种基于划分聚类的经典无监督学习算法，其基本思想是：在原始数据集合中，随机选择k个数据点，其初始值作为各个簇的中心。计算剩余非中心点的数据到各个簇中心的距离，将其分配到距离最近的聚类簇，然后重新计算每个簇的平均值，重新选取簇类中心点，不断重复，直至目标准则函数收敛[21]。准则函数的定义为：

(5)

准则函数可以保证生成的簇尽可能紧凑，不同的簇之间尽可能独立。

1.4 Hadoop平台

Hadoop具有吞吐量大、效率高、可靠性好及自动容错等优点，近年来在处理海量数据方面应用广泛。HDFS作为Hadoop的数据储存管理框架，由一个负责文件控制管理的主节点NameNode和若干个负责文件储存的从节点DataNode聚合成一个单一的全局文件系统。系统中的文件被分成数据块，并被复制储存在若干个从节点中，默认数据块大小为64 MB。HDFS框架的可靠性体现在其将每一个数据块分别复制储存在3个独立的从节点中，如果一个数据块数据丢失，额外的副本数据仍可调用。

MapReduce是Hadoop的数据计算框架，适用于并行处理海量数据的分布式模型。Map(映射)函数和Reduce(归约)函数是该框架的2大主要操作。将源数据文件按需求分成若干数据块，以键值对的形式作为Map函数和Reduce函数的输入输出。其中，key为聚类类别；value为数据对应维度和与数据对象个数的累加值。数据块通过相互独立、并行的Map函数计算产生输出值，输出值排序、合并，将key值相同的运算结果作为Reduce函数的输入值进行计算归约并输出。MapReduce的工作流程如图2[22]所示。

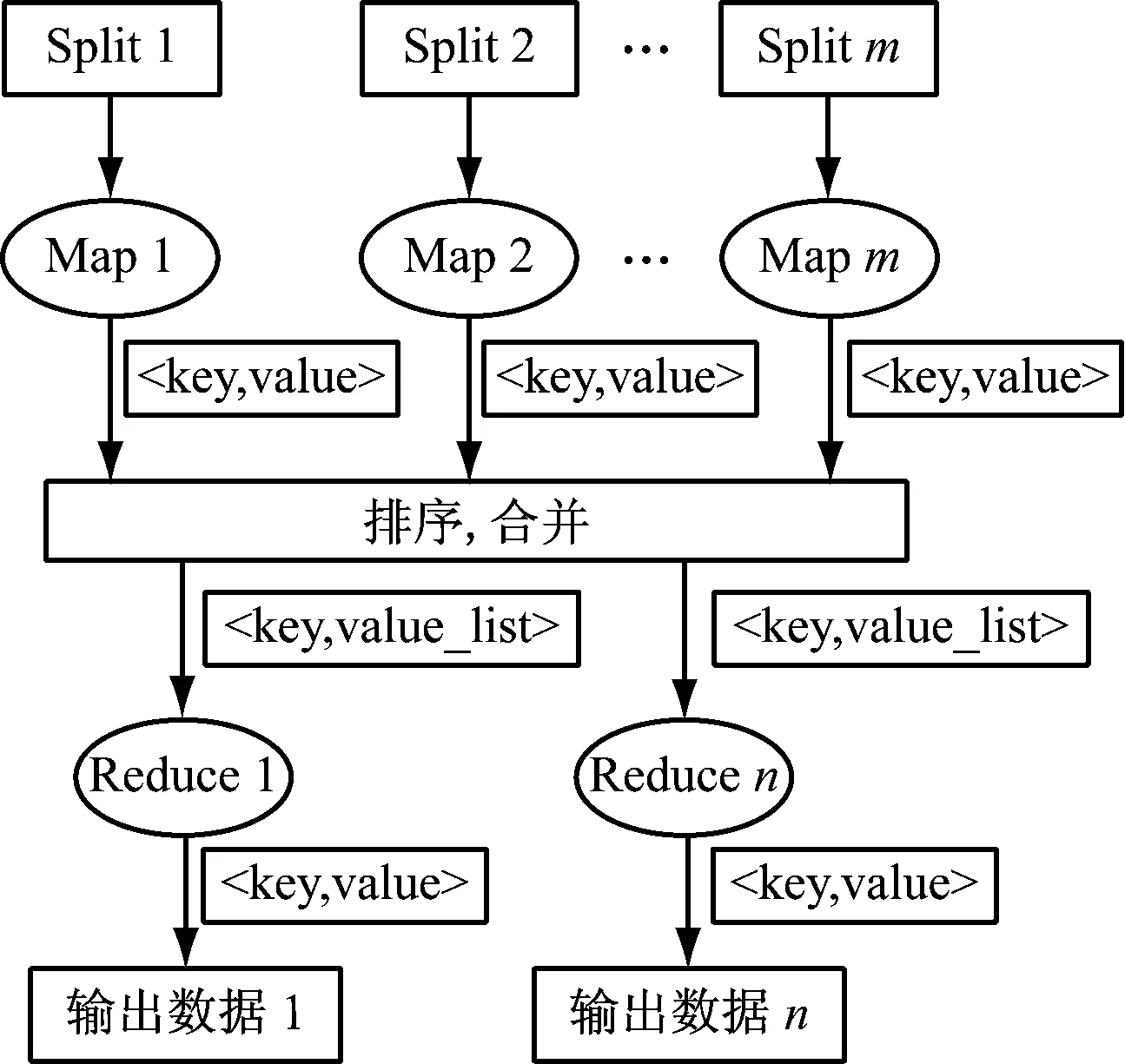
图2 MapReduce工作流程

2 RCK-means新算法流程

RCK-means算法采用基于MapReduce的顺序组合编程模型，对源数据属性约简后，按顺序采用MapReduce将算法分成2个子框架(即Canopy框架和K-means框架)完成。如图3所示，具体算法流程如下：

(1) 根据粗糙集属性约简需求建立初始决策表，确定条件属性和决策属性，依据决策属性与条件属性的依赖度进行属性约简，剔除冗余数据，形成新数据集。

(2) Canopy算法Map阶段，将属性约简的新数据集转化成键值对形式发送到m个Map函数中。计算各个数据点距离阀值，将距离值与D1、D2进行比较并分类，经迭代生成Canopy集合。

(3) Canopy算法Reduce阶段，将Map阶段输出结果并集计算，生成数据集合Q。对集合Q进行Canopy处理，不断重复直至数据集合为空，得到聚类簇K及其中心点，作为K-means框架的输入值。

(4) K-means算法Map阶段，根据Canopy框架得到的聚类簇，将聚类簇以键值对形式输入，计算每个节点数据到各个簇中心的距离，并将其分配至距离最近的簇，标记其聚类类别，以键值对形式输出。

(5) Combine函数对Map函数的输出值进行划分处理，在本地完成同一簇数据的合并，将簇中数据所对应的维度值求和，并计算数据对象个数，以键值对形式输出。

(6) K-means算法Reduce阶段，接收Combine函数输出值，解析各簇中数据对应维度值之和以及数据对象的总个数，得到新的聚类中心，并进行下一轮迭代，直至收敛。

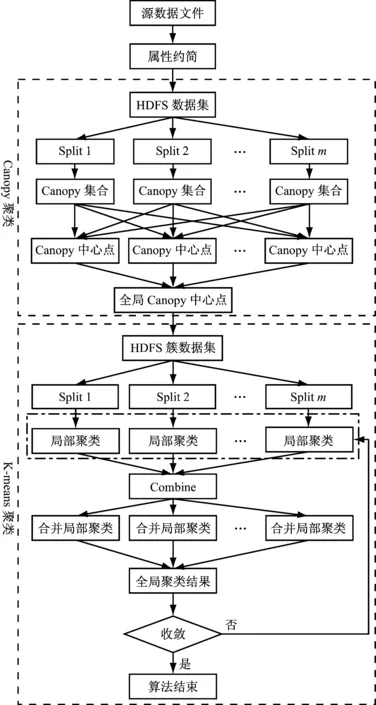
图3 RCK-means算法工作流程

3 改进RCK-means算法在锅炉效率优化中的应用

3.1 大数据技术应用于电站锅炉效率优化中的意义

电站锅炉的节能降耗一直以来都是电站机组优化控制的关键，锅炉效率作为反映机组经济性、环保性的重要参数，其优化问题备受关注。目前，锅炉效率优化技术主要分为2类[23]：一类是通过改造燃烧器和受热面来提高锅炉效率，或是通过安装先进检测设备实时精确控制锅炉运行重要参数。这类方法技术成熟、效果明显，但耗费大量人力和财力。另一类是在DCS基础上，利用人工智能、数据挖掘等方法寻找最优运行参数，实现锅炉效率优化。 这类优化方法依赖于建立精确优化模型和科学方便的优化算法，通常优化模型方法存在建模复杂、泛化能力差及样本获取困难等缺点，实用效果不佳。

大数据挖掘技术以电站DCS系统积累的海量运行数据为基础，以严谨的运算逻辑为依据，从热力系统自身运行数据中分析挖掘影响锅炉效率的因素，虽然挖掘得到的最优运行参数值与理论最优值存在一定偏差，但其诠释了运行参数的历史最优可达值。笔者基于改进的K-means聚类算法结合Hadoop大数据处理框架，在海量运行数据中利用各数据集(簇)聚类中心点寻找影响锅炉效率的最优数据集(簇)，经过详实的理论依据和数学验证对海量运行数据进行挖掘，得到的挖掘结果具有极强代表性和可靠实际应用性，可对现场运行提供指导作用。

3.2 大数据挖掘对象

以某600 MW燃煤机组锅炉为研究对象，该锅炉采用摆动四角切圆燃烧器，选取2013-03-01—2013-05-31的运行数据129 600条，采样周期为60 s。

3.3 确定大数据挖掘目标

笔者将锅炉效率作为挖掘目标，通过RCK-means算法确定影响锅炉效率的可调控运行参数，在典型负荷下，利用各聚类中心点与锅炉效率的对应关系挖掘最优性能参数，用于指导实际运行。锅炉效率的影响因素众多，以下分析各运行可调参数对锅炉效率的影响，以此为基础选取相关参数。

(1) 排烟氧量。

排烟氧量即过量空气系数，在燃烧过程中，过量空气系数过小，会使锅炉未完全燃烧损失增加，燃烧不充分，锅炉效率降低；过量空气系数过大，可减少不完全燃烧损失，但会增加排烟损失，锅炉效率降低。因此，选取适当的过量空气系数范围，对提高锅炉效率与经济运行至关重要。

(2) 磨煤机给煤量。

锅炉负荷在一定范围内，磨煤机组合差异及不同的煤量分配比会使火焰中心高度发生变化。火焰中心高度过高，将造成炉膛出口温度升高及对流换热量增加，各段工质吸热量发生变化，从而影响锅炉效率。

(3) 一、二次风参数。

一次风对锅炉炉膛温度有着极其重要的影响，炉膛温度高，燃烧着火快，燃烧速度快，使燃烧更加完全；但炉膛温度过高，会使燃烧逆反应加快，造成燃烧不完全。此外，一次风提高煤粉气流温度，可使煤粉着火提前，燃料燃烧时间充分，飞灰含碳量减少。二次风对着火稳定性和燃烧燃尽过程起着重要作用。一、二次风的配合为炉内提供良好的空气动力场，使得煤粉与空气充分混合，保证煤粉完全燃烧。同时，二次风可加强扰动混合，破坏煤粉表层的燃尽灰层，有利于燃烧完全。

在锅炉正常运行工况下，锅炉一次风由燃料量按比例控制，即在实际运行过程中，一次风量与相应的燃料量线性相关，故一次风不作为选用参数。

(4) 燃烧器摆角。

对于四角切圆燃烧器锅炉而言，燃烧器的摆动不但会造成火焰中心偏移，还会使切圆直径发生变化，因此燃烧器摆角会对锅炉效率产生影响。

(5) 排烟温度和飞灰含碳量。

锅炉排烟温度和飞灰含碳量同样是影响锅炉效率的重要参数。锅炉排烟热损失过高或过低都会对锅炉的经济性和安全性产生影响。飞灰含碳量增加将造成锅炉效率降低。排烟温度和飞灰含碳量属于燃烧状态监测参数，反映燃烧效率和燃烧状态，因此不作为运行可调参数。

综上所述，排烟氧量、磨煤机煤量、燃烧器摆角、一次风及二次风参数等都是影响锅炉效率的重要因素，同时煤种质量和环境温度等外界条件也对锅炉效率影响很大。在选取确定煤种(准格尔烟煤)和冷风温度(10～20 ℃)的情况下，通过选取与锅炉效率密切相关、可实际调控的运行参数作为大数据挖掘对象，挖掘影响锅炉效率的最优目标值。表1为大数据挖掘的运行参数对象。

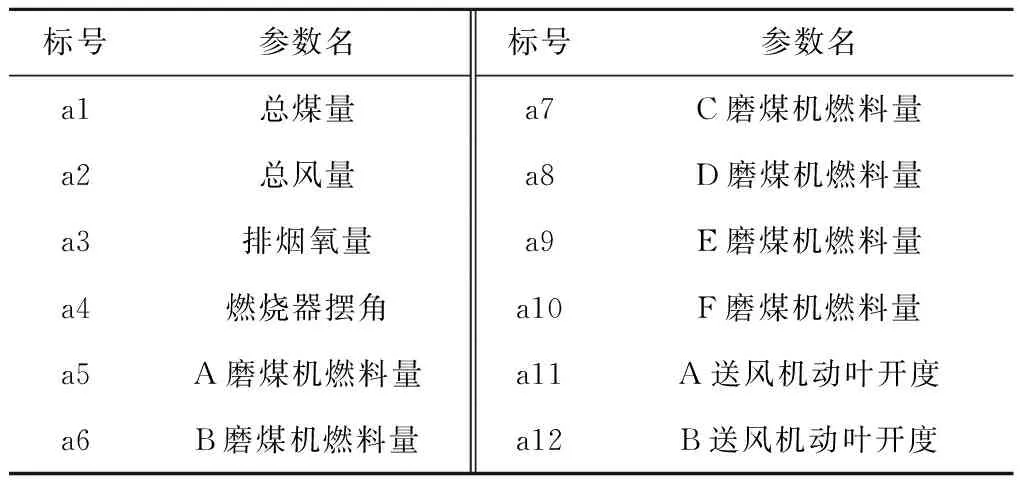
表1 锅炉可调运行参数

3.4 大数据预处理

大数据预处理作为大数据挖掘技术至关重要的一环，主要包括下面几个步骤：数据清洗、数据集成、数据转换和数据归约[24]。

由于DCS中历史数据在收集过程中含有异常和噪声数据较多，因此数据清洗过程格外重要。笔者采用的大数据处理方法本质是通过数据区间划分来进行大数据分析和最优解挖掘的，因此采用凝聚层次聚类等相关操作剔除离散点数据。

粗糙集理论属性约简的不可分辨关系决定了其只可处理离散型数据，而在DCS中采集的数据一般被认为是连续型数据，因此在属性约简前需对数据进行离散化。数据离散化方法多种多样，传统的离散化方法对区间分割点的选取十分困难，而区间划分结果对粗糙集分析也会产生很大影响，离散差异容易造成有价值数据丢失。笔者采用模糊集与粗糙集相结合的模糊粗糙集离散方法[25]，利用模糊性和粗糙性2种不确定性数学方法形成的数据相似度对数据集合进行“柔化分”和属性约简。这种方法可有效克服粗糙集对边界值过于苛刻的缺点，同时避免了有价值数据的丢失。

3.5 Hadoop平台搭建

首先在服务器上安装Linux Centos 6.5操作系统，并设置root用户自动访问，再下载解压Hadoop-1.2.1及JDK-1.6.0并安装，其间要保证服务器上Hadoop和JDK的安装路径HADOOP_HOME和JAVA_HOME一致。然后设置SSH免密码登录以实现各节点间的无密码访问，同时保障数据传输的安全性。Hadoop平台的配置主要是对conf/core-site.xml、conf/mapred-site.xml和conf/hdfs-site.xml 3个文件进行配置。其中，conf/core-site.xml文件设置Hadoop的全局属性参数，conf/mapred-site.xml文件设置MapReduce的运行任务参数，conf/hdfs-site.xml文件设置HDFS的数据备份参数。完成Hadoop基本配置后，在Hadoop根目录下对HDFS执行格式化命令，查看各节点运行状况并运行Hadoop环境。

3.6 大数据挖掘算法应用及结果

用第2.1节所示基于Pawlak属性重要度的决策表属性约简算法对所选数据进行属性约简，将12个运行参数作为条件属性，锅炉效率作为决策属性，其中每一个运行参数均被作为属性约简的一个属性。采用依赖度增量最大的启发式快速约简方法，设置依赖度增量阈值Δγ=0.005，当依赖度增量大于阈值时，则该属性归于约简中。由于A送风机动叶开度与B送风机动叶开度呈近似线性关系，其依赖度增量变化值小于Δγ，故将A送风机动叶开度作为一个约简，其他属性约简亦如此。经计算得到与原数据集具有相同分类能力且依赖度增量最大的属性约简集结果RED(P)={a3，a4，a12}，其中各约简的属性依赖度如表2所示。

应用RCK-means算法对约简后的数据集进行数据挖掘。设置Hadoop平台最小支持度为2%(即某负荷区间数据聚类个数不小于数据总数量的2%)。将锅炉负荷采用K-means聚类分为290～326 MW，327～357 MW，358～387 MW，388～415 MW，416～441 MW，442～477 MW，478～512 MW，513～544 MW，545～579 MW，580～603 MW等10个负荷段。根据算法流程对已约简数据集进行大数据挖掘，寻找各聚类中心点与锅炉效率对应关系的最优解。现以负荷388～415 MW的聚类结果为例进行分析，聚类结果如表3所示。表3中，第8类的锅炉效率最高，且类中有足够多的数据元组，可将其定为一个样本点。依此方法，选取其他各负荷区间聚类结果样本点，得到如表4所示的样本点集。

表2 约简属性依赖度

由表4可以得出负荷与各可调参数在确定煤种和冷风温度(10～20 ℃)下的优化曲线，现以排烟氧量的优化曲线和设计曲线为例进行对比。如图4所示，锅炉排烟氧量只给定了机组300 MW、450 MW和600 MW负荷工作点的设计数值，可以发现排烟氧量的设计值与优化值存在很大偏差。在低负荷时，排烟氧量优化值高于设计值，由于低负荷时锅炉着火及燃烧条件差，适当地增加排烟氧量有利于减少不完全燃烧热损失，提高锅炉效率；在负荷增加至约550 MW及以上时，锅炉燃烧趋于稳定，排烟氧量优化值逐渐减小，直至低于设计值，由于高负荷时锅炉燃烧稳定，适当地降低排烟氧量有利于减少排烟热损失。因此，在机组实际运行中，为保证不同运行工况下达到较高的效率，不能采用设计值，应分别对机组不同工况簇下的运行数据进行优化，选取各参数的最优目标值。图5和图6分别给出了燃烧器摆角及B送风机动叶开度的优化曲线以及机组300 MW、400 MW、500 MW和600 MW负荷工作点的习惯运行数值组成的运行曲线。由图5可知，燃烧器摆角的优化曲线与运行曲线存在一定差异，从优化曲线可以看出，随着负荷的增加，燃烧器摆角逐渐减小；当负荷达到400 MW时，燃烧器摆角呈增大趋势，由于负荷的增加，上层磨煤机启动，给煤量增加，火焰中心位置上升，二次风量增加，为防止炉膛出口烟气温度升高及对流受热面结渣，燃烧器摆角增大；随着负荷的不断增加，火焰中心位置上升，燃烧器摆角逐渐减小。由图6可知，送风机动叶开度的优化曲线与运行曲线大致趋势相同，但也存在一定差异。由优化曲线可知，在低负荷时，送风机动叶开度较小，当负荷达到375 MW时，送风机动叶开度逐渐增大，其原因是在高负荷时，为了控制污染物排放和防止燃烧器喷口结焦及总风量的限制，需要提高一、二次风配比，因此送风机动叶开度变大。

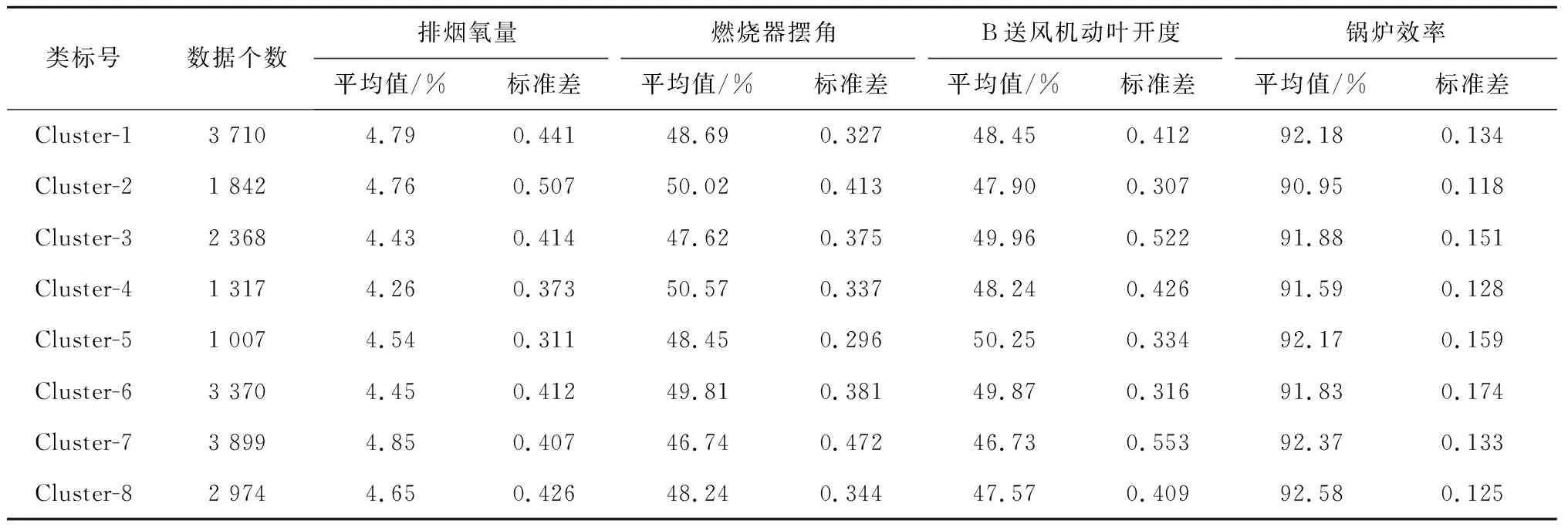
表3 第4负荷区间锅炉效率聚类分析结果

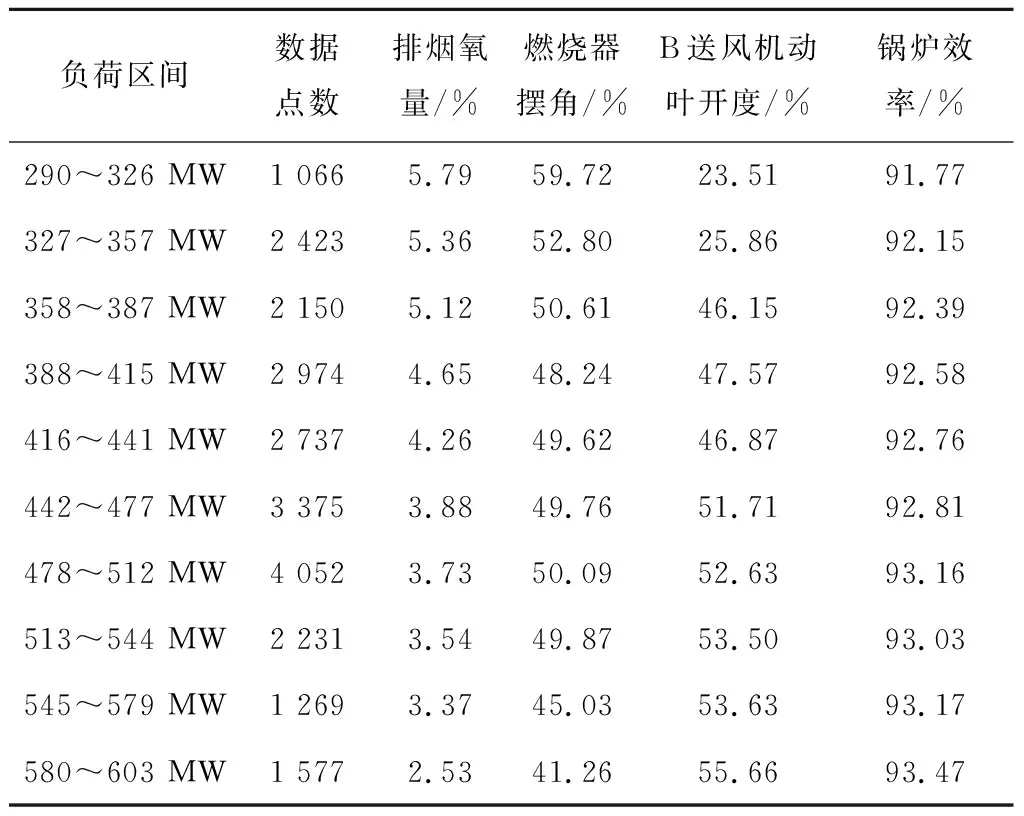
表4 各负荷区间对应锅炉效率最高的样本点

图4 排烟氧量的优化和设计曲线

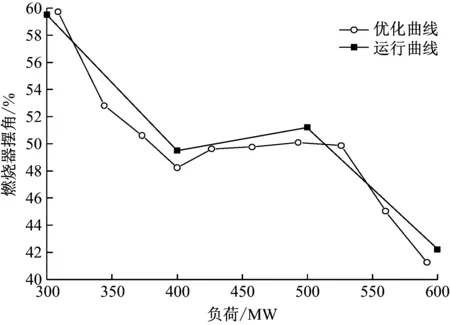
图5 燃烧器摆角的优化曲线

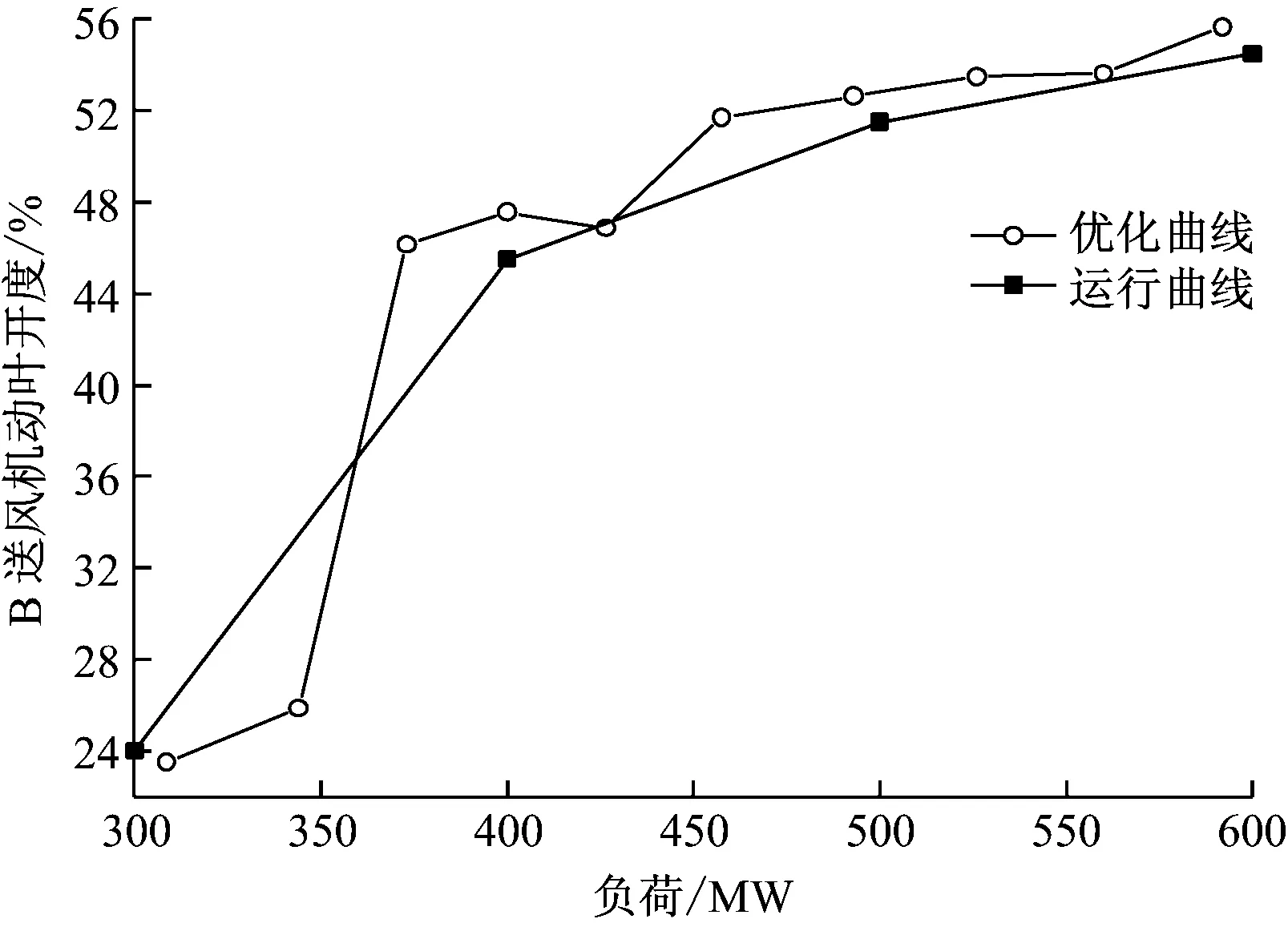
图6 B送风机动叶开度优化曲线

但应注意的是，得到的各个参数的优化曲线值不可单独考虑，各优化参数值是一个整体共存的关系，为使锅炉效率达到较高水平，应设置各优化参数均在最优值区间。锅炉效率的优化曲线与设计标准曲线的关系如图7所示。由图7可知，锅炉效率优化曲线的效率值较设计曲线提高很多，随着负荷的增加，优化值与设计值的差值变小。采用RCK-means算法选取影响锅炉效率的可调控运行参数进行锅炉效率大数据挖掘优化，经优化后锅炉效率可以达到历史较佳水平。

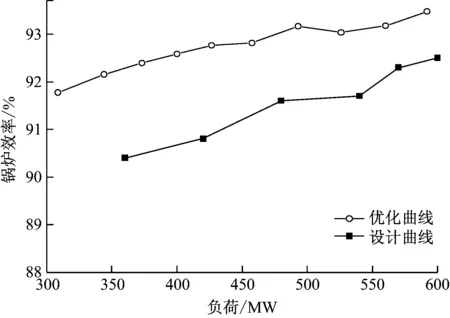
图7 锅炉效率的优化和设计曲线

4 结 论

合理确定运行参数优化目标值是火电机组优化运行的核心问题。基于大数据技术处理方法，挖掘出影响锅炉效率的最优运行参数。RCK-means新算法避免了出现局部最优解，提高了聚类准确率，剔除了冗余数据集，并极大地提高了聚类效率。同时，利用并行算法解决了传统数据处理方法无法胜任海量数据处理的不足。通过对电站机组实际运行数据进行挖掘，得到典型负荷下可调运行参数的最优目标值。在机组实际运行中，为保证不同运行工况下达到较高的锅炉效率，不能采用设计值，应设置各优化参数均在最优值区间，分别对机组不同工况簇下的运行数据进行优化，选取各参数的最优目标值。

参考文献：

[1] 齐敏芳, 付忠广, 景源, 等. 基于信息熵与主成分分析的火电机组综合评价方法[J].中国电机工程学报, 2013, 33(2): 58-64.

QI Minfang, FU Zhongguang, JING Yuan, et al. A comprehensive evaluation method of power plant units based on information entropy and principal component analysis[J].ProceedingsoftheCSEE, 2013, 33(2): 58-64.

[2] 付文峰, 侯艳峰, 王蓝婧, 等. 基于自适应粒子群算法的燃煤-捕碳机组热力系统优化设计[J].动力工程学报, 2016, 36(9): 746-752.

FU Wenfeng, HOU Yanfeng, WANG Lanjing, et al. Optimized design for thermodynamic system of coal-fired power plants with CO2capture based on AWPSO algorithm[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(9): 746-752.

[3] 崔超, 刘吉臻, 杨婷婷. 基于GA和模糊关联规则的锅炉脱硝经济性优化[J].动力工程学报, 2016, 36(4): 300-306.

CUI Chao, LIU Jizhen, YANG Tingting. Economical optimization of a boiler denitration system based on GA and fuzzy association rules[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(4): 300-306.

[4] 付忠广, 齐敏芳. 基于最大熵投影寻踪耦合的燃煤机组节能减排评价方法研究[J].中国电机工程学报, 2014, 34(26): 4476-4482.

FU Zhongguang, QI Minfang. Study on the evaluation method of energy-saving and emission reduction of coal-fired units based on projection pursuit method coupled with maximum entropy[J].ProceedingoftheCSEE, 2014, 34(26): 4476-4482.

[5] 余廷防, 耿平, 霍二光, 等. 基于智能算法的燃煤电站锅炉燃烧优化[J].动力工程学报, 2016, 36(8): 594-599.

YU Tingfang, GENG Ping, HUO Erguang, et al. Combustion optimization of a coal-fired boiler based on intelligent algorithm[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(8): 594-599.

[6] 高芳, 翟永杰, 卓越, 等. 基于共享最小二乘支持向量机模型的电站锅炉燃烧系统的优化[J].动力工程学报, 2012, 32(12): 928-933, 940.

GAO Fang, ZHAI Yongjie, ZHUO Yue, et al. Combustion optimization for utility boilers based on sharing LSSVM model[J].JournalofChineseSocietyofPowerEngineering, 2012, 32(12): 928-933, 940.

[7] 赵欢, 王培红, 钱瑾, 等. 基于模糊C-均值聚类的锅炉监控参数基准值建模[J].中国电机工程学报, 2011, 31(32): 16-22.

ZHAO Huan, WANG Peihong, QIAN Jin, et al. Modeling for target-value of boiler monitoring parameters based on fuzzy C-means clustering algorithm[J].ProceedingsoftheCSEE, 2011, 31(32): 16-22.

[8] 钱瑾, 王培红, 李琳. 聚类算法在锅炉运行参数基准值分析中的应用[J].中国电机工程学报, 2007, 27(23): 71-74.

QIAN Jin, WANG Peihong, LI Lin. Application of clustering algorithm in target-value analysis for boiler operating parameter[J].ProceedingsoftheCSEE, 2007, 27(23): 71-74.

[9] QIAN Weining, ZHOU Aoying. Analyzing popular clustering algorithms from different viewpoints[J].JournalofSoftware, 2002, 13(8): 1382-1394.

[10] MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]//Proceedingsofthe5thBerkeleySymposiumonMathematicalStatisticsandProbability. Berkeley, USA: University of California Press, 1967.

[11] 王意洁, 孙卫东, 周松, 等. 云计算环境下的分布存储关键技术[J].软件学报, 2012, 23(4): 962-986.

WANG Yijie, SUN Weidong, ZHOU Song, et al. Key technologies of distributed storage for cloud computing[J].JournalofSoftware, 2012, 23(4): 962-986.

[12] 王彦明, 奉国和, 薛云. 近年来Hadoop国内外研究综述[J].计算机系统应用, 2013, 22(6): 1-5, 28.

WANG Yanming, FENG Guohe, XUE Yun. Summary of Hadoop research in recent years in foreign countries[J].ComputerSystems&Applications, 2013, 22(6): 1-5, 28.

[13] 赵莉, 侯兴哲, 胡君, 等. 基于改进K-means算法的海量智能用电数据分析[J].电网技术, 2014, 38(10): 2715-2720.

ZHAO Li, HOU Xingzhe, HU Jun, et al. Improved K-means algorithm based analysis on massive data of intelligent power utilization[J].PowerSystemTechnology, 2014, 38(10): 2715-2720.

[14] 王德文, 孙志伟. 电力用户侧大数据分析与并行负荷预测[J].中国电机工程学报, 2015, 35(3): 527-537.

WANG Dewen, SUN Zhiwei. Big data analysis and parallel load forecasting of electric power user side[J].ProceedingsoftheCSEE, 2015, 35(3): 527-537.

[15] 宋亚奇, 周国亮, 朱永利, 等. 云平台下并行总体经验模态分解局部放电信号去噪方法[J].电工技术学报, 2015, 30(18): 213-222.

SONG Yaqi, ZHOU Guoliang, ZHU Yongli, et al. Research on parallel ensemble empirical mode decomposition denoising method for partial discharge signals based on cloud platform[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(18): 213-222.

[16] 万祥, 胡念苏, 韩鹏飞, 等. 大数据挖掘技术应用于汽轮机组运行性能优化的研究[J].中国电机工程学报, 2016, 36(2): 459-467.

WAN Xiang, HU Niansu, HAN Pengfei, et al. Research on application of big data mining technology in performance optimization of steam turbines[J].ProceedingsoftheCSEE, 2016, 36(2): 459-467.

[17] PAWLAK Z. Rough sets[J].InternationalJournalofComputer&InformationSciences, 1982, 11(5): 341-356.

[18] 胡可云, 陆玉昌, 石纯一. 粗糙集理论及其应用进展[J].清华大学学报(自然科学版), 2001, 41(1): 64-68.

HU Keyun, LU Yuchang, SHI Chunyi. Advances in rough set theory and its appliations[J].JournalofTsinghuaUniversity(ScienceandTechnology), 2001, 41(1): 64-68.

[19] 李天瑞, 罗川, 陈红梅, 等. 大数据挖掘的原理与方法——基于粒计算与粗糙集的视角[M]. 北京: 科学出版社, 2016: 24-31.

[20] 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J].软件学报, 2008, 19(1): 48-61.

SUN Jigui, LIU Jie, ZHAO Lianyu. Clustering algorithms research[J].JournalofSoftware, 2008, 19(1): 48-61.

[21] 高榕, 李晶, 肖雅夫, 等. 基于云环境K-means聚类的并行算法[J].武汉大学学报(理学版), 2015, 61(4): 368-374.

GAO Rong, LI Jing, XIAO Yafu, et al. Parallel algorithm based on K-means clustering in cloud environment[J].JournalofWuhanUniversity(NaturalScienceEdition), 2015, 61(4): 368-374.

[22] 王德文, 刘晓建. 基于MapReduce的电力设备并行故障诊断方法[J].电力自动化设备, 2014, 34(10): 116-120.

WANG Dewen, LIU Xiaojian. Parallel fault diagnosis based on MapReduce for electric power equipments[J].ElectricPowerAutomationEquipment, 2014, 34(10): 116-120.

[23] 杨婷婷. 基于数据的电站节能优化控制研究[D]. 北京: 华北电力大学, 2010.

[24] 方洪鹰. 数据挖掘中数据预处理的方法研究[D]. 重庆: 西南大学, 2009.

[25] WU Weizhi, MI Jusheng, ZHANG Wenxiu. Generalized fuzzy rough sets[J].InformationSciences, 2003, 151: 263-282.