跨声速压气机转子叶顶区域流场非定常计算和POD分析
刘震雄, 竺晓程, 杜朝辉
(上海交通大学 机械与动力工程学院, 工程热物理研究所, 上海 200240)
符号说明:
p——压力,Pa
T——总温,K
λ——特征值
f——转子通过频率,Hz
t——转动周期,s
跨声速轴流式压气机转子的叶顶间隙流动对压气机的稳定性和性能具有重要的影响,叶顶间隙流动复杂,是压气机研究设计中最为棘手的问题之一。自从Rains[1]首次针对叶顶间隙流动开展研究以来,国内外许多学者通过叶顶间隙流动相关理论与先进的实验手段得到了叶顶间隙流动的基本结构和流动特征。研究表明,叶顶区域的流动损失占据叶片总流动损失的30%以上,并且会诱发旋转失速的产生。
Adamczyk等[2]对跨声速压气机转子NASA 67叶顶区域流场进行数值模拟,发现随着流量的减小,叶顶间隙泄漏涡的运行轨迹在沿转子轴向方向上向周向偏转,激波和泄漏涡造成的堵塞区也向前移动,最终导致数值计算发散。Schlechtriem等[3]研究了跨声速压气机近失速状态下由激波导致的叶顶间隙泄漏涡的破碎现象,破碎的叶顶间隙泄漏涡会覆盖流场中大部分区域,引起堵塞急剧增加,从而导致失速。Vo[4]通过研究整个压气机内部流动失稳中叶顶间隙泄漏流流动以及流场的非定常发展规律,提出了判断轴流压气机出现突尖型失速先兆诱发失速的准则。
韩少冰等[5]通过实验研究了叶顶间隙泄漏流与压气机叶栅三维角区分离的相互作用,结果表明随着叶顶间隙尺寸及叶栅内气流折转程度的增加,叶顶间隙泄漏涡与上通道涡间的相互作用逐渐增强。刘宝杰等[6-7]利用实验技术重现了叶片通道内叶顶间隙泄漏流的演化过程。
本征正交分解(POD)方法早在1967年首次在流场分析中被采用[8],是模态分解方法中的一种形式,其基本思想是根据已有样本数据计算得到一组最能够代表这组数据的正交基函数,在构造这组基函数时使得样本数据在正交基上的投影分量按次序依次迅速衰减[9],可将高维数据降阶投影到低维空间,从而获得数据的物理特征。目前,POD方法已用于研究翼型的反设计[10]、流动结构分析[11]、跨声速翼型的抖振分析[12]及圆柱不稳定线性动力学问题的建模过程[13]等,但用于分析压气机叶顶间隙流场结构特性的研究还没有。
综上所述,虽然目前国内外学者对跨声速压气机转子叶顶区域的流动研究很多,但对其产生的非定常特性还没有统一的认识,而且不同类型压气机的叶顶区域流场的非定常特性具有不同的表现形式。笔者采用数值模拟的方法研究跨声速压气机转子叶顶区域流场的非定常特性及其发展规律,采用POD方法提取叶顶区域流场结果的POD模态,寻找引起叶顶间隙流场非定常波动的主导模态,并揭示影响跨声速压气机转子稳定性的因素,以提高压气机的工作裕度和性能。
1 研究对象
研究对象为NASA的Rotor35孤立转子[14],转子数为36,展现比和轮毂比分别为1.19和0.7,设计叶顶转速为454 m/s,设计压比和质量流量分别为1.865和20.18 kg/s,设计转速为17 188 r/min。图1为该转子子午面流道示意图。

图1 Rotor35子午面流道示意图
为减少在计算区域进、出口边界处的数值反射对转子叶片前缘流场以及后缘流场的不良影响,在建立计算区域时将前后计算区域分别延长2倍左右叶片轴向弦长的长度。
2 数值模拟方法
采用CFX 15.0商用软件进行数值模拟,结合k-ε湍流模型求解相对坐标系下的三维雷诺时均N-S方程,对单流道进行定常和非定常计算。为准确模拟转子叶顶区域的流场特性,空间离散格式采用高分辨率格式,非定常计算采用隐式双时间步方法,在叶片转动一个栅距的时间内设定20个物理时间步,每一个物理时间步下的虚拟时间步为10步。
Rotor35为跨音速压气机转子,叶片的叶型弯扭程度很大,需要对其网格进行较好地划分以保证计算精度。计算区域的网格划分采用CFX软件的TURBOGRID,如图2所示。在流道进、出口段计算区域采用H型网格,在叶片区域采用J型网格进行拓扑,近叶片表面的区域采用O型网格围绕控制,在转子的叶顶间隙处沿径向均匀布置17个网格节点。整个计算区域网格的正交性大于20°,所有边界层高度小于3×10-5m。

(a) 转子单流道网格

(b) 转子叶根处网格

(c) 叶顶间隙网格
数值计算中进口给定总温为288 K,总压为101 325 Pa,采用轴向进气,机匣和轮毂壁面都定义为静止,壁面采用绝热无滑移边界。非定常计算以定常计算收敛结果为初场,通过调节出口压力得到不同工况下的非定常流场,当非定常计算中性能参数呈现出周期性波动即认为数值计算已收敛。
为验证数值模拟的准确性,计算了Rotor35在100%设计转速下的总性能特性,其总性能特性曲线与试验测量结果的对比见图3,其中的质量流量以堵塞点质量流量为基准进行了无量纲化,NPE代表近峰值效率点,NS代表近失速点。从图3可以看出,在整个质量流量范围内,数值模拟所得总性能特性曲线与试验测量结果的变化趋势一致。

(a) 总压比

(b) 绝热效率
Fig.3 Comparison of compressor performance between calculation results and actual measurements
为了进一步验证数值计算的可靠性,选取定常计算中的近峰值效率点,比较了计算和试验得到的总压比和总温比沿叶高方向的分布,如图4所示。从图4(a)可以看出,沿叶高方向,两者的总压比变化趋势基本一致,在数值上略微有所差别。在图4(b)中,两者的总温比吻合较好。
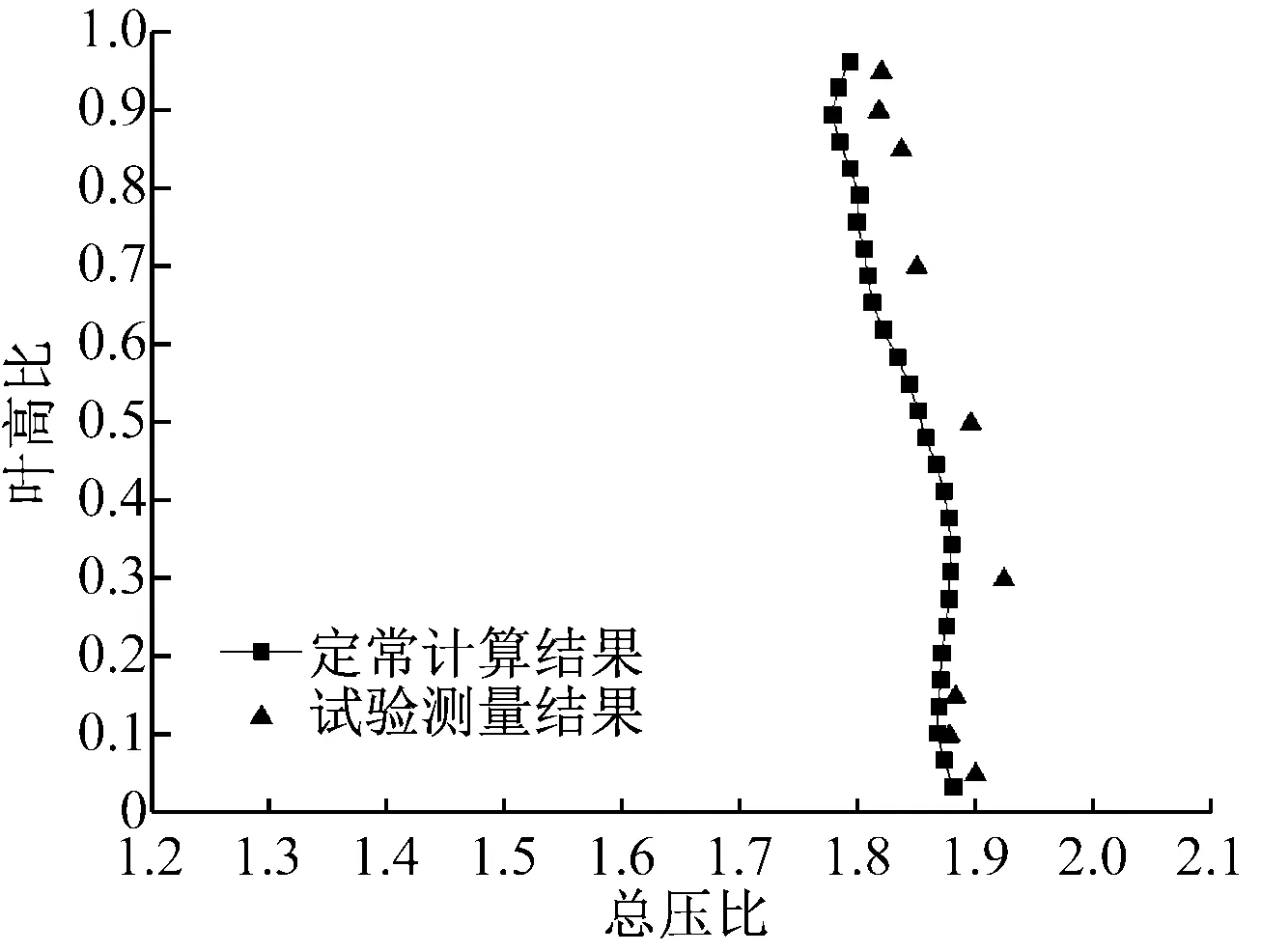
(a) 总压比

(b) 总温比
Fig.4 Span-wise distribution of total pressure ratio and total temperature ratio under NPE condition
通过数值计算结果与试验测量结果的对比分析,数值模拟方法能很好地预测压气机转子总性能特性以及流场细节。因此,可以采用该计算方法研究跨声速压气机转子叶顶区域的流动特性。
3 叶顶区域流场的非定常分析
3.1 叶顶间隙泄漏流的频谱特征
图5为近失速点工况下99%叶高处叶顶间隙泄漏流某时刻的熵分布云图。从图5可以看出,在叶栅通道内熵值变化剧烈,熵增明显,并且向叶片前缘逐渐增大,在叶顶间隙泄漏涡处达到最大值,表明随着质量流量的减少叶顶间隙泄漏涡与激波的干涉强度增大,并且干涉区域向上游移动。从图5还可以看出,在近失速点工况下,主流与转子叶顶间隙泄漏流之间形成了熵增交界面,并向转子前缘移动且与转子叶顶前缘平面平行,对主流的流动产生了阻碍作用。

图5 近失速点工况下99%叶高处某时刻的熵分布云图
转子叶片流动波动区域主要集中在叶高80%以上的区域,为分析叶顶区域波动的非定常特性,在转子叶顶区域布置一系列监测点,在压力面99%叶高位置沿弦向布置12个监测点,沿叶顶间隙泄漏涡轨迹附近布置8个监测点,具体位置如图6所示,压力面附近的监测点为Ps1~Ps12,叶顶间隙泄漏涡附近的监测点为Tp1~Tp8,记录下各监测点静压时域信号并进行频谱分析,获得叶顶区域流场的非定常频率。
图7为近峰值效率点工况下,叶顶区域部分监测点的静压时域信号。由图7可知,在整个非定常计算过程中,静压时域信号不随时间呈现出波动特性,在计算收敛后一直保持恒定,叶顶区域流场处于稳定状态。

图6 叶栅通道压力监测点位置示意图
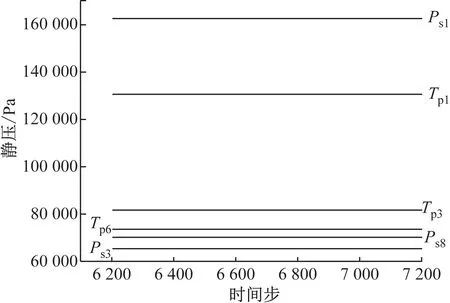
图7 近峰值效率点工况下叶顶区域监测点的静压时域信号
图8给出了近失速点工况下叶顶区域压力面Ps1点处的静压时域信号以及Ps1~Ps12点处静压时域信号的快速傅里叶变换(FFT)分析。从图8可以看出,监测点的静压随时间表现出很强的周期性波动特性。叶顶区域压力面监测点的非定常频率约为0.56倍转子通过频率,该波动频率并非转子叶片固有的转子通过频率,而是叶顶间隙泄漏流的非定常频率,振幅在叶片前缘位置最大,在叶片弦向其他位置处相对较小。

(a) 叶顶区域压力面Ps1点的静压时域信号

(b) 叶片压力面Ps1~Ps12点的频谱分析
Fig.8 Static pressure signal of pointPs1and FFT results of pointsPs1toPs12in tip region on pressure surface under NS conditon
图9给出了近失速点工况下叶顶间隙泄漏涡轨迹附近Tp3点的静压时域信号以及Tp1~Tp8点处静压时域信号的FFT分析。从图9可以看出,监测点的静压随时间同样呈现出很强的周期性波动特性,叶顶间隙泄漏涡轨迹附近各监测点静压时域信号的非定常频率同样为 0.56倍转子通过频率。

(a) 叶顶间隙泄漏涡附近Tp3点的静压时域信号

(b) 叶顶间隙泄漏涡附近Tp1~Tp8点的频谱分析
图9 近失速点工况下叶顶间隙泄漏涡轨迹附近Tp3点静压时域信号和Tp1~Tp8点的频谱分析
Fig.9 Static pressure signal ofTp3and FFT results of pointsTp1toTp8in tip leakage vortex under NS condition
3.2 叶顶区域流场的非定常特性
为深入了解叶顶区域的非定常特性,图10和图11分别给出了一个波动周期t内叶顶区域的瞬态流场及负轴向速度云图。由图10可以看出,叶顶间隙泄漏流主要由2部分组成,一部分为叶顶间隙泄漏涡,在定常计算中,叶顶间隙泄漏涡在激波后出现破碎,在非定常计算中,可以观察到叶顶间隙破碎的泄漏涡随时间在不断变化;此外在叶顶区域还存在另外一个明显的漩涡运动过程,如叶顶间隙泄漏流流线图中的黑色圆圈所示区域,称为叶顶二次涡。在 1/6t时刻叶顶间隙泄漏涡经过激波后发生破碎,并与叶顶二次涡紧靠在一起没有发生分离,两者在一起发生翻转。在2/6t时刻叶顶二次涡与叶顶间隙泄漏涡即将完全分离,二次涡紧靠转子叶片压力面并有少量流体绕过叶片前缘。在3/6t时刻叶顶二次涡紧贴叶片压力面向后发展,在4/6t时刻叶顶二次涡继续沿压力面向叶片下游移动。在5/6t时刻叶顶二次涡强度明显减弱,但在叶片前缘流道中叶顶间隙泄漏涡旁又有一个新的叶顶二次涡开始形成。在7/6t时刻叶顶间隙泄漏涡与叶顶二次涡在压力面侧相互作用,回到1/6t开始时刻的流场,完成一个周期波动。在5/6t时刻可以看出,叶顶二次涡发生的位置紧靠叶顶间隙泄漏涡遇到激波后的破碎点,并随之往下游运动。从该涡的流线可以看出,叶顶二次涡并不仅仅是叶顶间隙泄漏涡的衍生涡,而是由激波与叶顶间隙泄漏涡形成的破碎、通道中部未形成泄漏涡的相邻叶片泄漏流流线以及来流一起形成的,是叶顶区域非定常周期性波动形成的必要条件。

(a) 1/6t(b) 2/6t(c) 3/6t(d) 4/6t(e) 5/6t(f) 7/6t
图10 叶顶区域的流线图
Fig.10 Flow field in tip region
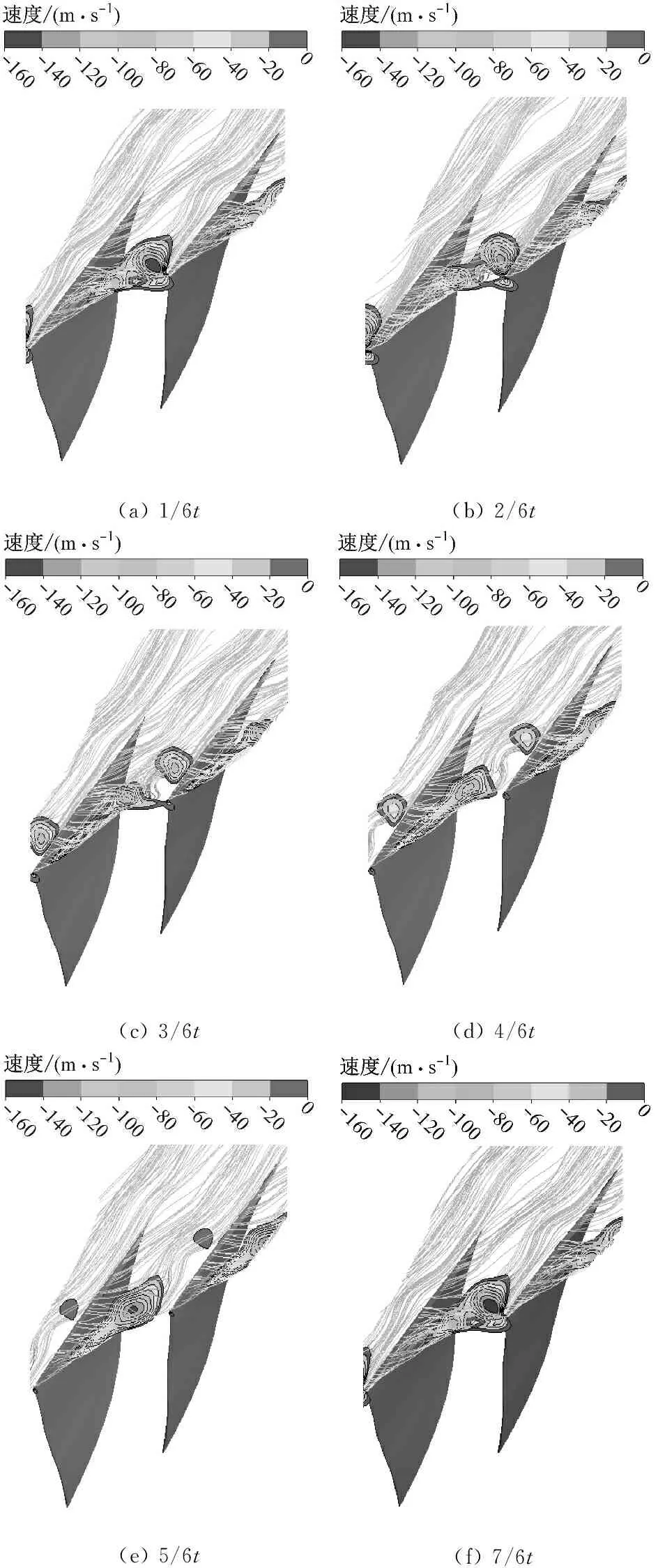
(a) 1/6t(b) 2/6t(c) 3/6t(d) 4/6t(e) 5/6t(f) 7/6t
图11 叶顶区域负轴向速度云图
Fig.11 Negative axial velocity in tip region
图11显示叶栅通道中部激波后始终存在一个低速反流区。在1/6t时刻可以看到在叶顶间隙泄漏涡中形成分离涡,在叶顶前缘出现一个低速反流区。在2/6t时刻分离涡脱离叶顶间隙泄漏涡并向叶片压力面移动,并且有少量流体绕过叶片前缘进入下一流道。在3/6t时刻叶顶间隙泄漏涡反流的区域延伸出一道狭长区域至前缘,此时叶顶间隙泄漏涡的强度最大,分离涡沿压力面向下游移动,反流区域彻底脱离。在4/6t时刻脱离的分离涡沿叶片压力面继续向下游移动,在5/6t时刻分离涡强度逐步减弱,并且观察到在叶顶间隙泄漏涡心破碎处又有新的二次涡线开始产生。回到7/6t时刻,重新开始一个新的波动周期。从叶顶负轴向速度云图中可以看到叶顶二次涡为相对封闭的分离涡,因此在速度反流云图中可以看出其比叶顶间隙泄漏涡弱,且受叶顶间隙泄漏涡的影响很大。
4 叶顶区域流场的POD分析
4.1 POD方法
采用快照POD方法进一步分析叶顶区域的非定常流动。首先假定有一组随时间变化的参数,并将每个时刻的参数信息称为一个快照。快照POD方法的第一步是将上述N个时刻即快照的参数波动部分均写入一个矩阵:
(1)
式中:u由空间位置上所需关注的参数(速度、静压等)组成;M为该组参数的元素个数。
要计算POD模态,首先应计算相关矩阵C:
C=UTU
(2)
由于矩阵C为自协方差矩阵,因此具有非负特征值,求解特征值问题可以表示为:
CA=λA
(3)
求解上述特征值后将特征值从大到小进行排列,即λ1≥λ2≥λ3≥λ4>…>0,相应的特征向量也随之排序。
利用排列好顺序的特征向量可以得到POD的各阶模态:
(4)
式(4)中分母所用的范数可以定义为:
(5)
至此每个快照的参数均可由POD各阶模态的线性组合来表示,而各阶模态的系数被称为POD系数,各个快照的POD系数可以通过下式得到:
an=ΨTun
(6)
其中,Ψ=φ1φ2…φN。而每个快照参数又可以采用POD模态重构得到:
(7)
采用POD方法分解流场信息数据,一般用前几阶的模态就可以表示出流场的主要结构,并可以近似重构流场信息。这样在分析流场信息时就可以从原来分析各个时刻的流场数据转为研究POD前几阶模态所显示的流场数据,可大量减少分析数据的工作量,提高效率。
4.2 叶顶区域流场的POD分析
为提取压气机转子叶顶区域流场参数分布的POD模态,基于以上单流道转子流场的非定常计算结果,共选取了100个近失速点工况下99%叶高处的瞬时流场结果作为POD的快照,相应的取样时间长度为压气机转子非定常波动周期的3倍左右,由于给出了100个瞬时流场的计算结果,故有100个模态和对应的特征值。为便于观察、提高效率,取由大到小排列的特征值中前30阶特征值的衰减曲线(见图12),POD特征值大小即相应POD模态能量占系统总能量的多少。从图12可以看出,第一阶模态的能量远高于其他模态的能量,随着模态阶数的上升,模态的能量衰减十分迅速,前几阶模态能量之和占据了流场总能量的大部分,表明前几阶模态对流场结构起到主要作用,即前几阶POD模态包含了非定常流场的主要流动信息。因此分析前几阶模态所包含的流动信息,有助于进一步认识压气机转子叶顶区域非定常流场的主要流动特征。

图12 POD模态的特征值
图13给出了能量最大的前四阶POD模态所描述的静压云图。由于各阶模态的范数不同,为了更好地对比不同阶模态的流场信息,对各阶模态的数据针对各自极值进行了归一化处理。
POD模态分析可以获取流场中能量最高的流动相干结构。图14(a)为能量最大的第一阶模态表征的压力云图,其拥有与时间序列压力云图基本一致的分布结构。激波在叶片前缘分离形成脱体激波,激波后形成逆压梯度,同时从叶片吸力面前缘开始形成低压槽区域,根据涡动力原理,其对应着叶顶间隙泄漏涡轨迹,在叶片压力面从前缘至尾缘的压力分布相对均匀。这些流场信息表明POD的第一阶模态捕捉到了叶栅通道内的主要流场结构。在第二阶模态的压力云图中,叶片压力面前缘存在明显的低压区域和高压区域,以脱体激波为分界面,叶片表面上的压力变化较大。同样,在第三阶和第四阶模态的压力云图中,叶片表面上的压力分布不均匀,在激波附近存在压力间断,特别在第四阶模态压力云图中,在叶片压力面前50%弦长范围内出现多个成对的低压区域和高压区域,压力波动更加剧烈、频率更高,叶片吸力面前缘开始出现表征叶顶间隙泄漏涡的低压槽,第四阶模态进一步细化了激波间断区域和压力波动,使流场信息更接近实际流场。

(a) 1/6t

(b) 2/6t

(c) 3/6t

(d) 4/6t

(e) 5/6t

(f) 7/6t
图13 各时间序列叶顶区域流场静压云图
Fig.13 Pressure contour of blade tip region at different time series
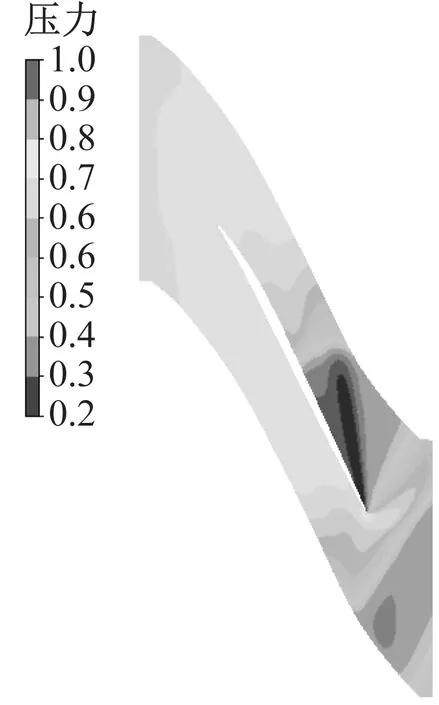
(a) 第一阶模态

(b) 第二阶模态

(c) 第三阶模态

(d) 第四阶模态
POD前四阶模态的模态系数随时间的变化如图15所示。从图15可以看出,第一阶模态的模态系数最大,波动幅度也最大,与其他模态的模态系数相比占有绝对的主导地位。随着模态阶数的提高,模态系数的振幅减小,且第四阶模态的模态波动频率升高。对模态系数波动进行FFT频谱分析,发现前三阶模态的模态系数频谱分析结果均为6 382 Hz,约为0.61倍转子通过频率,与非定常计算中叶顶区域流场监测点的波动频率大致相同。第一阶、第二阶与第三阶模态波动波峰之间各相差约90°的相位,这主要由POD模态分解的正交性决定。
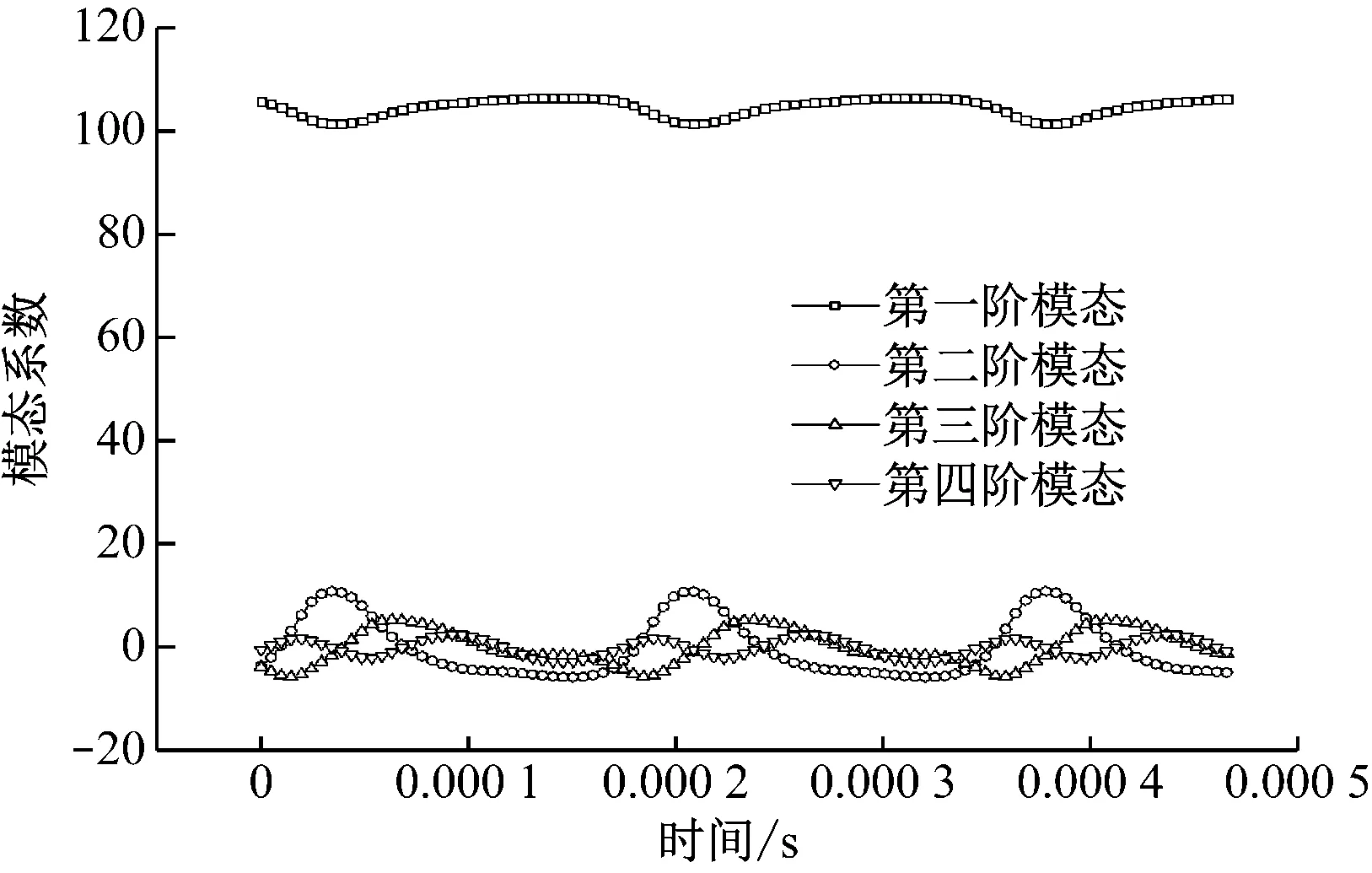
图15 模态系数随时间的变化
5 结 论
(1) 在大质量流量工况下,转子叶顶区域流场稳定,监测点参数不随时间波动;在近失速点的小质量流量工况下,叶顶区域流场呈现周期性的波动特性,监测点的非定常频率约为0.56倍转子通过频率。由激波与叶顶间隙泄漏涡形成的破碎、通道中部未形成泄漏涡的相邻叶片泄漏流流线以及来流一起形成的叶顶二次涡是叶顶非定常周期性波动形成的必要条件。
(2) 根据POD模态分析,最大能量的第一阶模态捕捉到了叶栅通道内的主要流场结构,更高阶的模态进一步细化了流场中的激波间断区域和压力波动。模态系数的频谱分析表明,前三阶模态的波动频率与叶顶区域流场的非定常频率基本相同,是主导非定常周期性波动现象的主要模态,且前三阶模态的波动波峰之间各相差约90°的相位。
参考文献:
[1] RAINS D A. Tip clearance flows in axial compressors and pumps[D]. Pasadena, USA: California Institute of Technology, 1954.
[2] ADAMCZYK J J, CELESTINA M L, GREITZER E M. The role of tip clearance in high-speed fan stall[J].JournalofTurbomachinery, 1993, 115(1): 28-38.
[3] SCHLECHTRIEM S, LÖTZERICH M. Breakdown of tip leakage vortices in compressors at flow conditions close to stall[R]. Orlando, Florida, USA: ASME, 1997.
[4] VO H D, TAN C S, GREITZER E M. Criteria for spike initiated rotating stall[J].JournalofTurbomachinery, 2008, 130(1): 011023.
[5] 韩少冰, 钟兢军, 陆华伟, 等. 叶尖泄漏与压气机叶栅三维角区分离相互作用实验研究[J].推进技术, 2013, 34(2): 187-193.
HAN Shaobing, ZHONG Jingjun, LU Huawei, et al. Experimental investigation on interaction between tip clearance flow and three-dimensional separation in compressor cascade[J].JournalofPropulsionTechnology, 2013, 34(2): 187-193.
[6] 刘宝杰, 张志博, 于贤君. 轴流压气机转子叶尖泄漏堵塞特性的试验研究[J].航空学报, 2013, 34(12): 2682-2691.
LIU Baojie, ZHANG Zhibo, YU Xianjun. Experimental investigation on characteristics of tip leakage blockage in an axial compressor[J].ActaAeronauticaetAstronauticaSinica, 2013, 34(12): 2682-2691.
[7] LIU Baojie, YU Xianjun, LIU Huoxing, et al. Application of SPIV in turbomachinery[J].ExperimentsinFluids, 2006, 40(4): 621-642.
[8] LUMLEY J L. The structure of inhomogeneous turbulence[M]//YAGLOM A M, TATARSKI V I.AtmosphericTurbulenceandWavePropagation. Moscow Russia: Nauka, 1967: 166-178.
[9] 王阿霞, 马逸尘, 付英. 基于双重网格法的非定常N-S方程POD数值模拟[J].纺织高校基础科学学报, 2009, 22(1): 76-81.
WANG Axia, MA Yichen, FU Ying. Proper orthogonal decomposition for the non-stationary Navier-Stokes equations based on two-grid method[J].BasicSciencesJournalofTextileUniversities, 2009, 22(1): 76-81.
[10] 张伟, 陈诚, 孙德军. 低Reynolds数横向排列双圆柱绕流的POD-Galerkin谱方法数值模拟[J].水动力学研究与进展, 2009, 24(1): 82-88.
ZHANG Wei, CHEN Cheng, SUN Dejun. Numerical simulation of flow around two side-by-side circular cylinders at low Reynolds numbers by a POD-Galerkin spectral method[J].JournalofHydrodynamics, 2009, 24(1): 82-88.
[11] COUPLET M, BASDEVANT C, SAGAUT P. Calibrated reduced-order POD-Galerkin system for fluid flow modelling[J].JournalofComputationalPhysics, 2005, 207(1): 192-220.
[12] BUI-THANH T, DAMODARAN M, WILLCOX K. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J].AIAAJournal, 2004, 42(8): 1501-1516.
[13] 李静, 张伟伟, 李新涛. 失稳初期的低雷诺数圆柱绕流POD-Galerkin建模方法研究[J].西北工业大学学报, 2015, 33(4): 596-602.
LI Jing, ZHANG Weiwei, LI Xintao. Researching method of building flow field of initial development stage of low Reynolds number flow past a circular cylinder[J].JournalofNorthwesternPolytechnicalUniversity, 2015, 33(4): 596-602.
[14] REID L, MOORE R D. Design and overall performance of four highly loaded, high speed inlet stages for an advanced high-pressure-ratio core compressor[R]. Cleveland, OH, USA: NASA, 1978.

