带型钢实腹梁转换结构静力弹塑性分析

杨维英

福州市建筑设计院

正文：

1 引言

随着我国经济的快速发展，建筑结构的形式日趋新颖，基于抗震性能设计必然是发展趋势[1-4]。基于性能的结构抗震设计能针对不同的抗震设防要求采取不同的抗震措施。钢——混凝土组合结构是一种新型结构，它扬长避短，能充分发挥钢结构和混凝土结构的材料特性，钢-混凝土组合结构用钢量少、刚度大、施工周期短、稳定性和整体性表现更强、抗火性和耐久性得到提高等。因此通过组合概念则可以钢材和混凝土的材料特性发挥到极致，形成一系列新颖、高效的结构体系。其在土木工程中得到广泛运用，例如我国的北京四川大厦、江西铜矿贮矿仓、四川旺苍东河大桥和美国的西雅图双联广场大厦等建筑，都全部或部分采用了组合结构。

本文主要对带型钢转换的框架-核心筒结构进行静力弹塑性分析，了解该结构的抗震性能，可以对该结构体系在多遇地震下弹性设计进行校核，又能确定该结构体系在罕遇地震作用下的破坏机制，找出其相应的薄弱环节，从而对薄弱环节进行加强，使整个结构达到预期的效果；同时也可为以后的设计和进一步研究作参考。

2 工程概况

本工程为某高层办公写字楼，结构设计使用年限为50年，抗震设防烈度为6度，丙类，设计地震分组为第一组，地震基本加速度为0.05g，建筑场地类别为Ⅱ类，基本风压为0.45kN/m2，地面粗糙度类别为C类。采用钢筋混凝土框架——核心筒结构体系，外框架平面尺寸为38.3m×23.3m，中央核心筒平面尺寸8.0m×8.0m，除去屋顶的两层机房地上共22层，建筑高度为86m。为了满足建筑使用功能，在第三层设置转换层，第一层、第二层和转换层层高为5m，如图2所示。本工程型钢混凝土中的型钢采用较常用的实腹式宽翼缘的H形轧制型钢，其构造图如图1所示。

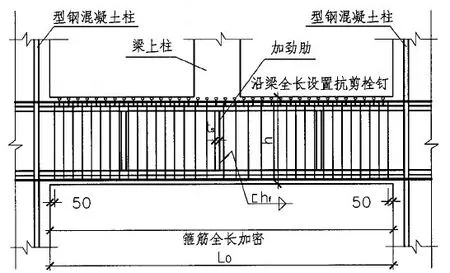
图1 H形型钢混凝土托柱梁的构造

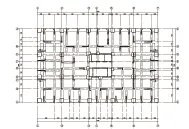
图2 转换层结构平面布置图

本工程转换梁的截面高度为2000×500mm，当采用普通梁式转换时，转换层上、下层刚度突变而形成薄弱层。根据文献[4]选择合适的带型钢的实腹梁截面尺寸，如表1和表2所示。

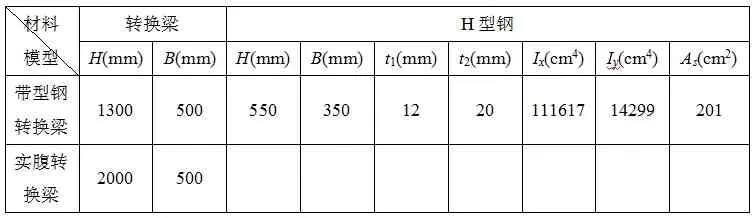
表1 转换梁截面尺寸

表2 转换梁的含钢率、配筋率、体积配箍率

3 整体结构的静力弹塑性分析

采用前文得到合理刚度比应用于此实际工程，整体结构模型如图3所示。Midas模型是根据PKPM结构模型转换过来的，其结构平面布置、各构件截面、荷载及相关参数的设定同PKPM结构模型。为确保计算模型的正确性，对两个模型的静力计算做了简单的误差对比分析见表3。

从表3可知，质量误差不超过2%，在工程误差允许的5%范围之内，说明PKPM模型转Midas模型荷载较为准确。Midas-Building中提供了两种POA分析方法，一种是基于荷载增量的荷载控制法，另一种是基于目标位移的位移控制法。本文进行静力弹塑性Push-over分析采用的是位移控制法，即基于性能的抗震设计，一般先通过静力分析确定发生最大位移的节点及该位移发生的方向，给定该节点设计控制位移的方法。该结构在X、Y向发生最大位移的节点都是在顶层角点位置，如图3所示位置，这两点分别控制结构X、Y方向的最大位移，控制位移设定为0.86m（即结构高度的1/100），然后逐渐增加荷载直到达到控制位移，以此来分析评估结构的综合性能。

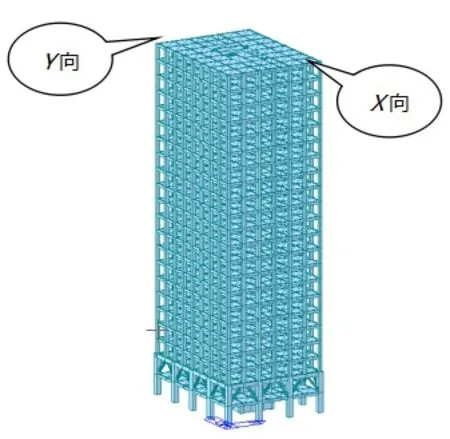
图3 Madis模型

3.1 确定结构的性能点

通过Midas软件对结构进行静力弹塑性分析，其中X向的刚度大于Y向的刚度，图4为结构在X、Y方向的能力谱——需求谱曲线关系。图中曲线依次表示结构在罕遇地震作用下阻尼比为5%、10%、15%、20%时的需求谱曲线，当结构构件达到屈服时，结构的阻尼不断增大，同时结构的刚度也会变化并影响下一步计算环节，依次循环而达到预定目标位移，从而验证结构是否满足抗震要求[5]。图4中蓝线与绿线的交点表示结构在罕遇地震作用下的性能控制点。

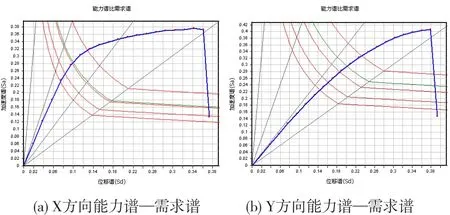
图4 能力谱-需求谱曲线

从图4中可以看出，结构在两个方向都有交点，验证了结构能够实现“大震不倒”的性能目标。该曲线比较光滑、变化比较均匀，随着位移的慢慢增大，结构的刚度连续退化、屈服、破坏，最后曲线出现了下降段。表4给出了结构在两个方向的性能控制点参数。

表4 性能控制点主要参数

3.2 位移角

从图5和6中可以看出，结构两个方向最大层间位移角分别为1/239（出现在第14层）和1/420（出现在第4层），满足规范要求；最大层间位移分别为0.01592m和0.00904m，分别出现在第14和4层，分别为建筑结构高度的1/5402和1/9513，位移与结构总高度的比值远小于2%，满足抗震性能要求。

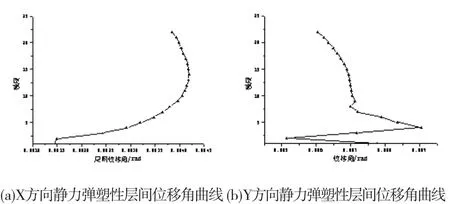
图5 静力弹塑性层间位移角曲线

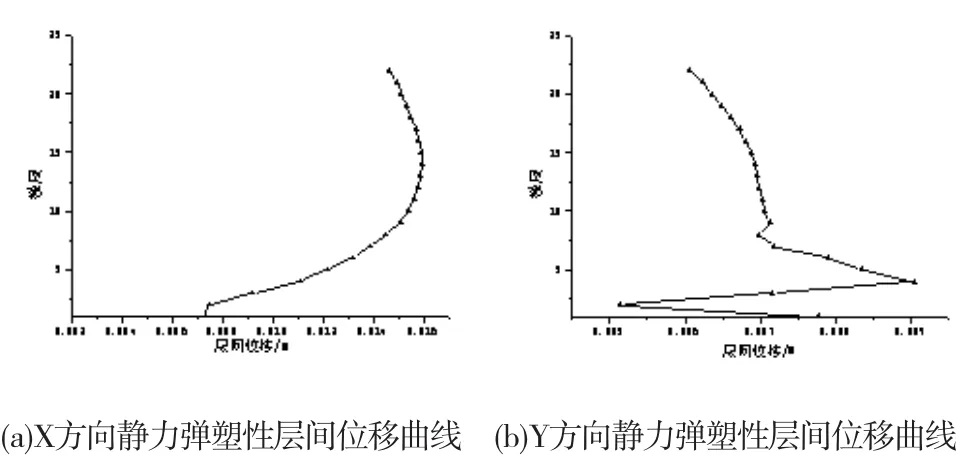
图6 静力弹塑性层间位移曲线

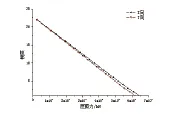
图7静力弹塑性层剪力移曲线

3.3 基底剪力-顶层控制点位移关系曲线

图8 给出了结构基底剪力与控制点位移的关系曲线，可以得到， X向，控制点位移=200.7mm时，结构开始屈服，基底剪力N=45447kN，位移Δ=573.3mm时，曲线出现下降段，结构开始破坏，基底剪力N=87888kN； Y向，控制点位移=114.7mm时，结构开始屈服，基底剪力N=51110kN，位移Δ=573.3mm时，曲线出现下降段，结构开始破坏，基底剪力N=81212kN。X、Y向的强屈比分别是1.934、1.589，说明带型钢转换结构拥有较高的强度储备。

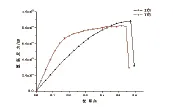
图8 带型钢转换结构基底剪力-顶层控制点位移关系曲线

3.4 结构出铰机制

图9 -10分别给出了整体结构的最终出铰图。其弹塑性发展过程为：核心筒部位的连梁两端和转换梁两端首先出现塑性铰，随着水平推力的逐步增大，框支柱也出现了塑性铰，框架梁和转换梁两端也不断有塑性铰出现，参与结构耗能。

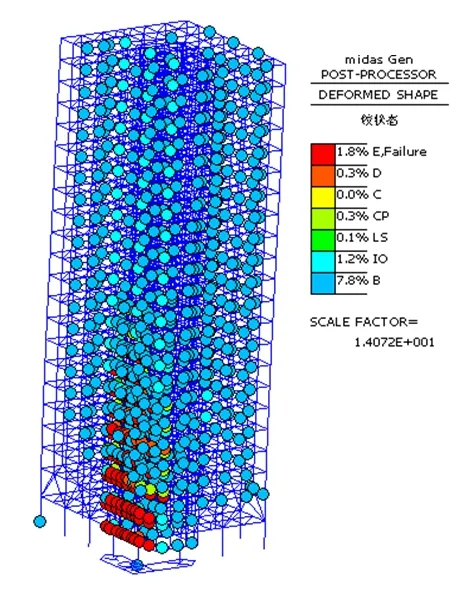
图9 X向工况整体结构最终出铰图

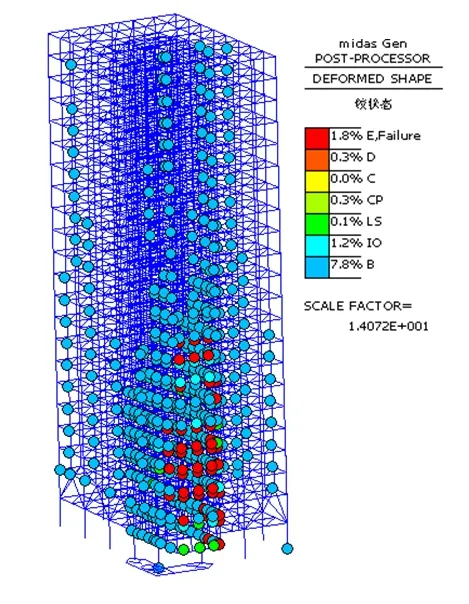
图10 Y向工况整体结构最终出铰图

4 结论

本章主要是通过对实际工程进行了采用带型钢转换高层进行静力弹塑性分析，了解其在罕遇地震作用下的抗震性能。用Madis Gen对带转换层的框架-核心筒结构进行静力弹塑性分析，简单介绍了计算模型的建立过程；通过数据分析，从结构大震作用下性能控制点的确定、层间位移角、层剪力、各构件塑性铰的发展情况等方面评估了其抗震性能。分析结果显示，整体结构首先在剪力墙连梁两端出现塑性铰，随着水平推力的继续增大，框架梁也开始屈服，参与结构耗能，带型钢转换结构的框架-核心筒结构能够很好的抵抗大震，框架能够很好的作为第二道抗震防线。