Seakeeping Prediction of SWATH with Three Dimensional Translating-pulsating Source Green Function

SUN Xiao-shuai,YAO Chao-bang,YE Qing

(Department of Naval Architecture Engineering,Naval University of Engineering,Wuhan 430033,China)

0 Introduction

Small-Water-Plane-Area Twin Hull(SWATH)ships are innovative concept of vehicles and special configuration.They consist of submerged twin hulls,an above water superstructure,and connecting struts.While the major part of the displaced volume is concentrated well below the free surface,the more slender struts are actually piercing the free surface.In such a way there will be less wave influence,so the vessel becomes very stable,even at higher speeds and in rough sea conditions.SWATH configuration results in long natural periods in heave,pitch and roll.Unlike the conventional passenger catamarans,SWATH no long suffer from slamming and slam induced whipping and unpleasant coupled motions which can lead to fatigue damage and kinetosis[1-3].Nowadays,SWATH has been widely used to construct passenger ferries,cruise ships,oceanographic research and diving support vessels and patrol vessels with different variations and increasing sizes.

Plenty of studies have been carried out on the seakeeping performance of the SWATHs.Lee[4-7]established a numerical method based on strip theory to evaluate the wave loads and motions of SWATH.The effect of the stabilizing fins was taken into consideration.The numerical results were in agreement with the experiment.Schellin[8]analyzed the influence of forward speed on the hydrodynamic interaction between the twin hulls.Murtedjo[9]calculated the motion of one SWATH by using two dimensional source distribution method.Due to the absence of viscous damping,the amplitude of roll was large when compared with experiment.

Li[10],Dong[11-12],Liu[13],Chen[14]and Lin[15]respectively developed the numerical method based on strip theory to investigate the influence of some factors on the seakeeping performance of SWATH,such as the configuration of the submerged twin hulls,the shape of the struts and the stabilizing fins.Mao[16]pointed out that it is of great significance to take the effect of viscosity and non-linearity into account when study the hydrodynamic performance of SWATH.

To the best of our knowledge,the majority of SWATH seakeeping simulations have been performed based on two dimensional strip theory.Though numerical methods based on three dimensional potential theory obtained remarkable achievements,only a few were applied to the seakeeping prediction of SWATH.Wu[17]utilized the commercial software Wasim to analyze the effect of speed,wave direction and slamming on the motion response of one SWATH.Qian[18]investigated a SWATH vehicle with inclined struts by 3D numerical simulations adopting a RANS method.

In the present study,a numerical method based on the Three Dimensional Translatingpulsating Source Green Function(3DTP)was established to obtain the wave loads and motions of SWATH.Some factors that may have great influence on the results are included in the equations of motions such as the wave interaction between the twin hulls,the viscous damping and the effect of stabilizing fins.Numerical simulations were conducted with one SWATH model named as SWATH 6A to validate the present method by comparisons with the strip theory and experiment.It can be concluded that the present method based on 3DTP gives better results of the wave loads and motions of SWATH.

1 Mathematical formulation

1.1 Coordinate system

Let o-xyz be the right-hand Cartesian coordinate system with xoy plane on the mean free surface and the x-axis is positive in the direction of the constant forward speed U of the SWATH.The z-axis is positive upward and crosses the center of gravity as shown in Fig.1.Dy is defined as the transverse distances between the centers of the twin hulls.

1.2 Velocity potentials

The regular incident wave is coming from a direction with an angle β,which is the angle between the positive x-axis and the incident wave direction.Thus 180°mean heading sea and the other wave directions can be found in Fig.1.The incident potential Φ0is given as below:

Fig.1 Coordinate system

whereis the wave number of the incident wave,ω0and ζ are the frequency and amplitude.ωeis the encounter frequency.The fluid is assumed ideal and incompressible of constant density.The irrotational flow is assumed throughout,and the surface tension effects are neglected.The velocity potential ΦT（x,y,z, t ）is introduced and can be written as:

where φsand Φ are the steady disturbance potential and unsteady potential,respectively.In the first order problem,all unsteady motions are assumed to be sinusoidal in time with the encounter frequency ωe,and by the linear decomposition,the unsteady potential Φ can be expressed in the form as below:

here ΦRand Φ7are the radiation and diffraction potentials in the field,and φ7is the time-independent part of Φ7.φjis the radiated wave potential due to the per unit amplitude motion in the jth mode of the ship,and ηjis the complex amplitude in the jth mode motion of the ship,where the cases j=1,2,…,6 correspond to surge,sway,heave,roll,pitch and yaw,respectively.

1.3 Boundary conditions

The potentials φj(j=1～7)must satisfy the Laplace equation together with boundary conditions,

where the generalized normal njis defined by （n1,n2,n3）=n and （n4,n5,n6）=r×n,with n is the outward unit normal vector on the hull surface and r is the position vector with respect to the center of the gravity of the ship.Neglecting the perturbation of the steady flow due to the presence of the SWATH,the mjcomponents of Eq.(5)can be simplified to mj=0 for j=1～4,m5=Un3and m6=-Un2.

2 Numerical methods

2.1 Boundary element integral equations and numerical solution

The solution of the above potentials φj(j=1～7)can be constructed by means of the 3D translating-pulsating source Green function for the boundary integral equation,which is formed by the surface integral over the mean wetted body surface and the free-surface contour integral along the intersection curves C between the body surfaces and the undisturbed free surface.

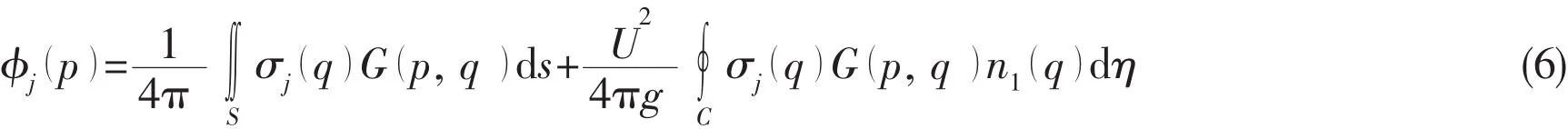
where G（ p, q ）is the translating-pulsating source Green function at the field point p （ x,y, z）due to a source of unknown strength σj（q ）at the source point p （ ξ,η, ζ）.

At this point,the Bessho form translating-pulsating source Green function is employed due to the fact that integration of this Green function and its derivatives over an elementary panel or the waterline segment can be expressed analytically.Single expression of Bessho form translating-pulsating source Green function can be expressed as

where,

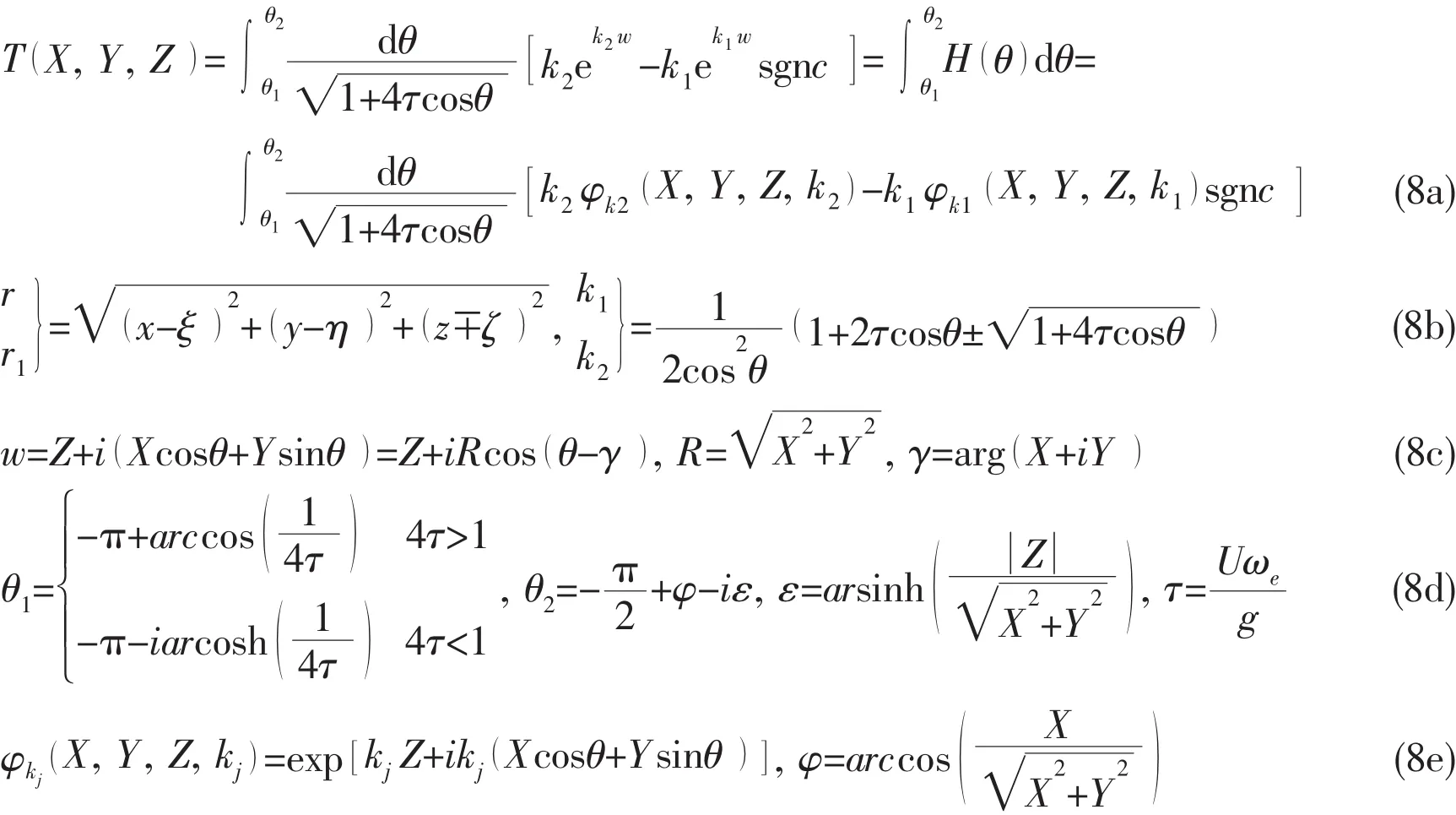
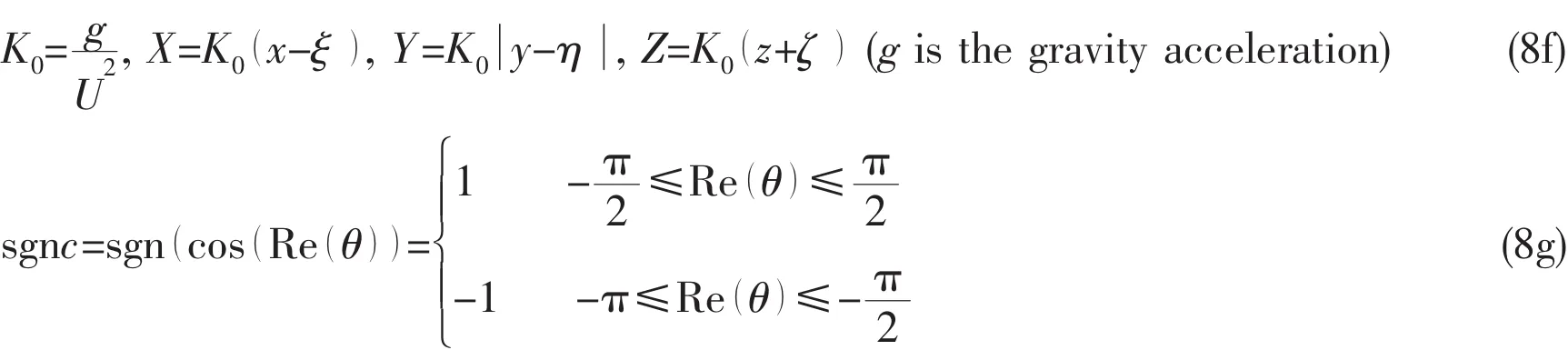
The analytical quadrature of this Green function over a panel and a waterline segment can be expressed as,

With Qlvertices of panel(l=1…N)and Slarea of triangle

Based on the variable substitution and the steepest descent integration method,a fast numerical calculation method for G,ISand ILcan be obtained[19].What should be pointed out is that the line integral in the second and third terms of Eq.(6)is of the form firstly introduced by Brard.It is derived from the linearized free surface condition,which includes the effect of the forward speed U on the x-directional component of the induced velocity by the source.

2.2 Wave exciting forces and hydrodynamic coefficients

Considering the unsteady state and omitting the high order terms and the static water pressure,the linear hydrodynamic pressure equation becomes

where ρ is water density.

After determining the velocity potential φjat any point on the mean wetted body surface of the ship,the radiation forces and moments in the j-th mode can be obtained by

From the radiation forces and moments expressed in Eq.(11),added mass coefficients Aijand damping coefficients Bijare obtained as

Wave exciting force and moments fwican be obtained by

2.3 Motion equations

Based on the rigid body dynamics,the motions in frequency domain for the SWATH can be obtained

where Mijis the element of the generalized mass matrices for the SWATH.Cijand Cbijis the element of 6×6 restoring force coefficient matrices of the SWATH.

2.4 Viscous damping coefficients

The viscous damping is usually ignored in the prediction of motions of conventional monohull since the wave-making damping predominated.However,as for SWATH,the submerged twin hulls does not generate large surface waves since they are well below the free surface.Thus the wave-making damping of SWATH in the vertical-plane modes is relatively small when compared with that of conventional monohull and it becomes necessary to take the viscous damping into consideration to get more reasonable results.

An empirical approach was employed to determine the viscous damping required to predict the motion.According to Lee[4],the vertical force of a harmonically oscillating body in regular waves with a constant forward speed will be assumed to be expressed as

where w is the relative fluid velocity with respect to the body,and α is the angle of incidence of flow at a cross section of the body at x position.

Under this assumption,the vertical force induced on the twin hulls can be obtained and the viscous damping coefficients can be derived.Details of expressions about the coefficients can be found in the work of Lee[4].

2.5 Stabilizing fins coefficients

The stabilizing fins installed on the inboard sides of the SWATH at certain longitudinal positions have been proved to improve the stability and considerably reduce the peak motion amplitude.However,it seems impossible to conduct an accurate evaluate of the lift generated by the fins since there are many hydrodynamic effects has to be taken into account,for instance,body-fin interaction,the blockage effect of the other hull,unsteady effect,the interaction of other fins,and so on.

To simplify the problem,only the body-fin effect will be included in the hydrodynamic coefficient.An empirical approach was followed and the coefficients derived by Lee[4]will be utilized in the present method.

3 Ship model

To validate the present numerical method,a SWATH vehicle known as SWATH 6A was selected to conduct simulations.The main parameters of SWATH 6A are given in Tab.1.

Tab.1 Main parameters of SWATH 6A

The panel distribution and profile view for SWATH 6A are shown in Fig.2.The mean wetted surface of SWATH ships is discretized in 1 752 panels and the shape of transverse sections of SWATH-6A is circle.The struts of SWATH 6A is normal,vertical and continuous along the submerged hull.

Fig.2 SWATH-6A

The dimensions of the stabilizing fins on SWATH 6A are illustrated in Tab.2 with installation positions.

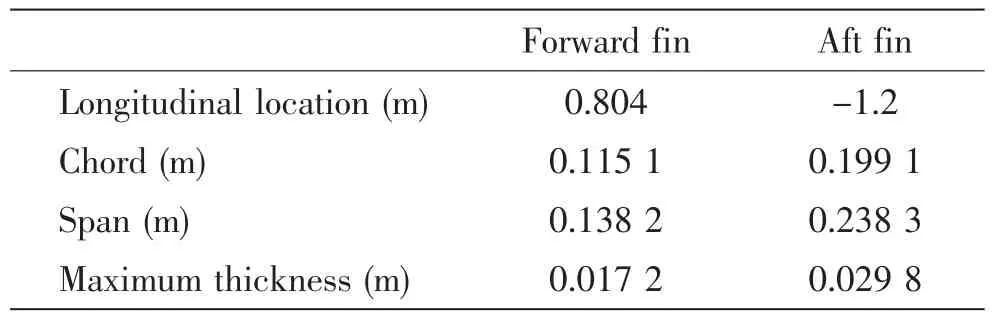
Tab.2 Parameters of stabilizing fins

4 Results and discussions

Numerical simulations based on 3DTP were carried out at two different forward speed,namely Fn=0 and Fn=0.538.Comparisons of normalized wave loads and motions between the present method,strip theory formulation(STF)and experiment conducted by Lee[20]were made to validate the present method.

4.1 Wave loads

The results of wave loads and motions in regular head waves obtained from different methods are given in Fig.3 and Fig.4.It can be seen that the heave forces of both numerical methods are in good agreement with that of experiment at both Fn=0 and Fn=0.538.While the pitch moments of numerical methods indicate the same trend when compared with that of experiment,they seem to underestimate the pitch moments.

Compared with the results of STF,the present method based on 3DTP gives almost the same values of heave force as the experiment at both zero speed and forward speed.As for pitch moment,the results of STF are well below that of the present method in moderate wavelength.

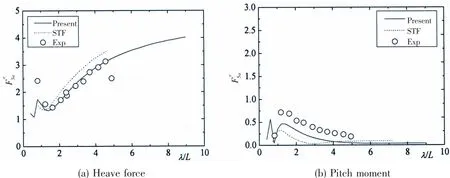
Fig.3 Wave loads of SWATH-6A at Fn=0

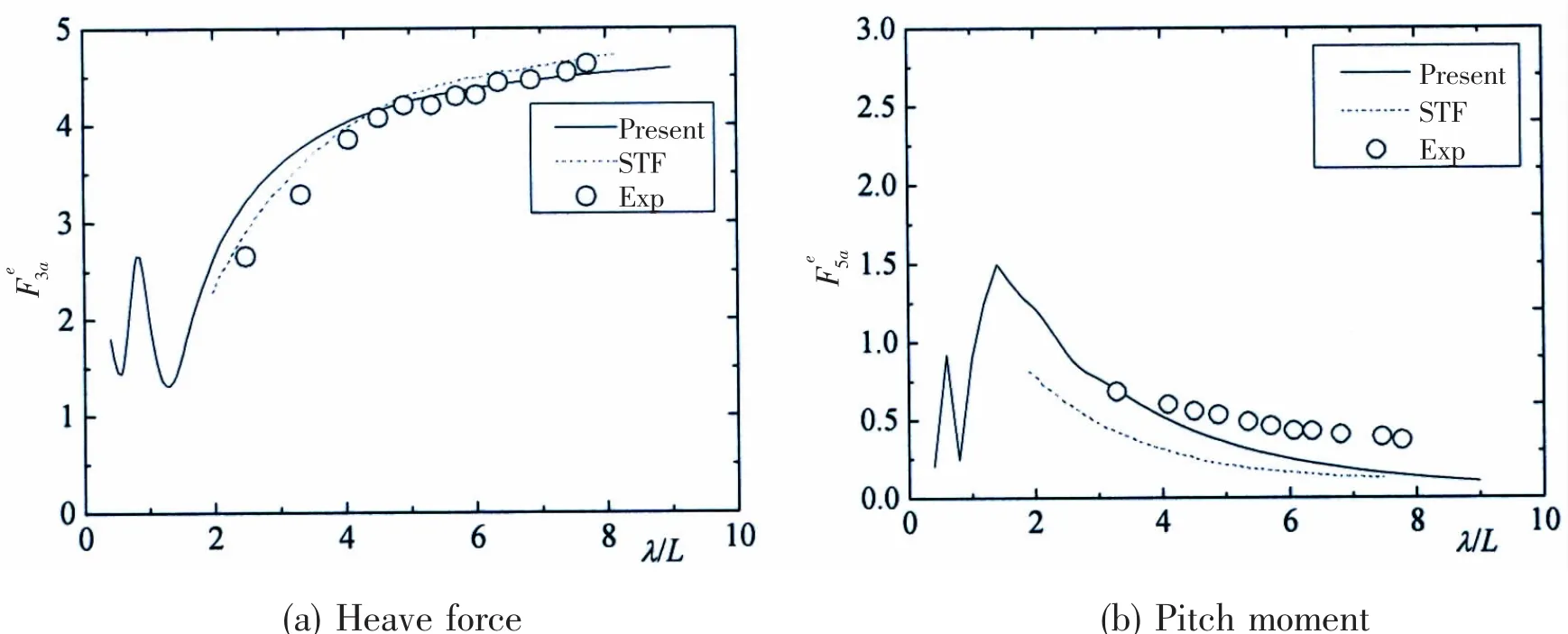
Fig.4 Wave loads of SWATH-6A at Fn=0.538

4.2 Motions in the vertical plane

The comparisons of heave and pitch responses from different methods are depicted in Fig.5 and Fig.6.Similar to the results of wave loads,the predictions of heave responses from numerical methods agree well with that of experiment.

The discrepancies between numerical methods and experiment are much more pronounced at pitch motions.The results of STF show a growing trend with the increase of wave length,while STF seems to give poor evaluation at Fn=0 and overpredict the pitch motions compared to the experiment at Fn=0.538.3DTP gives an exact prediction of pitch responses at Fn=0,even the drop near λ/L=2 is captured.With the increase of wave length,the amplitude of pitch motion predicted by 3DTP reaches a peak near λ/L=8.5,which is hard to validate due to the lack of experimental results.As for Fn=0.538,the results of 3DTP depict the same trend compared with experiment,but 3DTP seems to overpredict the pitch responses slightly except one point at λ/L=7.8.

Generally,it can be concluded that the motions are generally better predicted by the present method based on 3DTP than by the two dimensional strip theory,particularly for pitch motion.

Fig.5 Heave and pitch motion of SWATH-6A at Fn=0

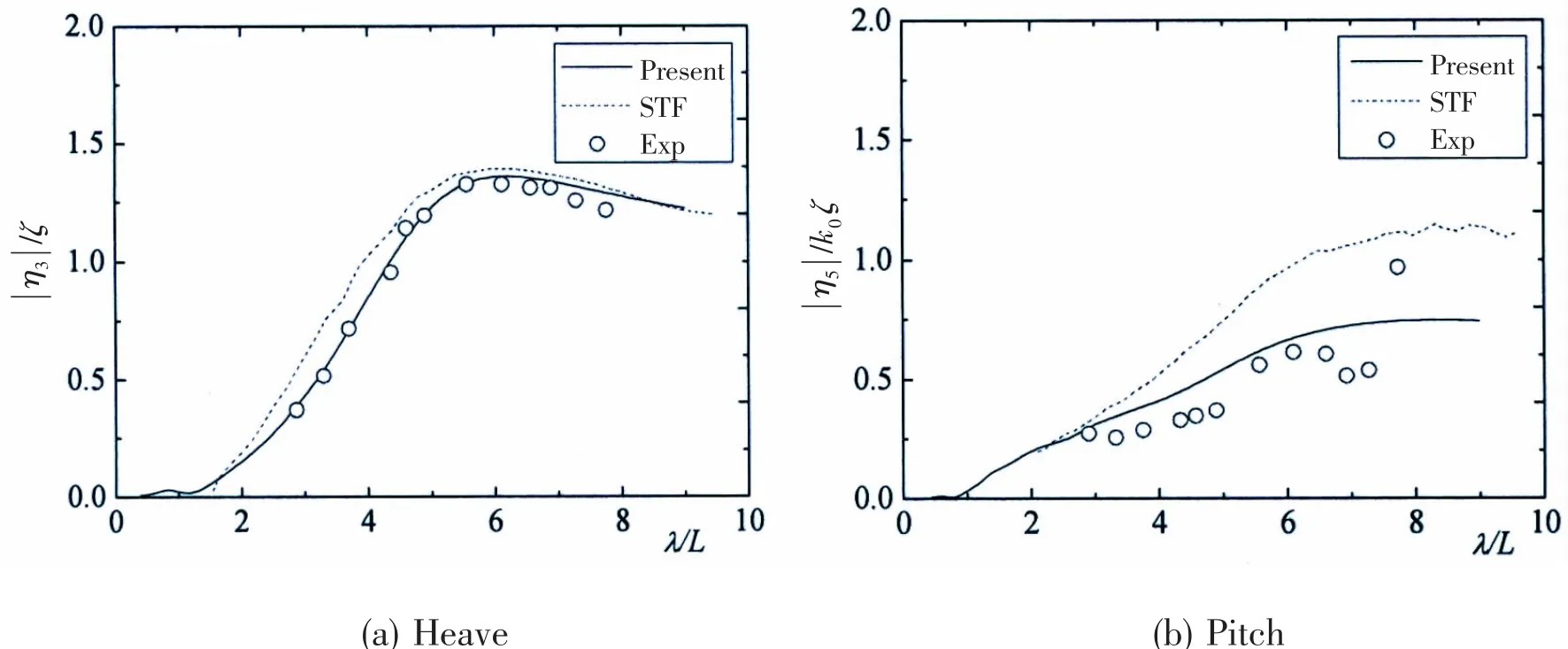
Fig.6 Heave and pitch motion of SWATH-6A at Fn=0.538

5 Conclusions

A numerical method based on the Three Dimensional Translating-pulsating Source Green Function(3DTP)was established to predict the seakeeping performance of SWATH.Some factors which differ from conventional monohulls were included in the equation of motions,such as the wave interaction between the twin hulls,the viscous damping and the effect of stabilizing fins.Numerical simulations were carried out to analyze the wave loads and motions of one SWATH vehicle known as SWATH 6A.Comparisons had been made to validate the present method with strip theory and experiment.It can be concluded that the motions are generally better predicted by the present method based on 3DTP than by the two dimensional strip theory,particularly for pitch motion.

[1]Kos S,Brcic D,Francic V.Comparative analysis of conventional and swath passenger catamaran[C]//Proceedings of 12th International Conference on Transport Science(ICTS).Portorož,Slovenija,2009:1-11.

[2]Lang T G,Sloggett J E.SWATH developments and performence comparisons with other craft[C]//International Conference on SWATH Ships and Advanced Multi-hulled Vessels.London,1985.

[3]Yaakob O B,Mekanikal F K.Development of a semi-swath craft for malaysian waters[R].University of Technology,Malaysia,VOT74204,2006.

[4]Lee C M.Theoretical prediction of motion of Small Waterplane Area,Twin-Hull(SWATH)ships in waves[R].DTNSRDC Report,SPD-76-0046,1976.

[5]Lee C M,Curphey R M.Prediction of motion,stability,and wave load of Small Waterplane Area Twin-Hull ships[J].Trans.Soc.Naval Architects and Marine Engineers,1977,85:94-130.

[6]Lee C M.Approximate evaluation of added mass and damping coefficients of two-dimensional SWATH sections[R].DTNSRDC Report,SPD-78/084,1978.

[7]Lee C M,McCreight K K.Investigation of effects of activated fins on vertical motion of a SWATH ship in waves[R].DTNSRDC Report SPD-763-01,1977.

[8]Schellin T E,Papanikolaou A.Prediction of seakeeping performance of a SWATH ship and comparison with measurements[C]//Proceedings of 1st international conference on fast sea transportation.Trondheim,Norway,1991:1-17.

[9]Murtedjo M,Djatmiko E B.Prediction of motion characteristics on SWATH type floating structure using two-dimensional frank close-fit technique[J].Journal Mekanikal Bil,2004,18:46-65.

[10]Li Xiangqun.A study on the seakeeping ability of SWATH[J].Journal of Shanghai Ship and Shipping Research Institute,1988,2:41-46.(in Chinese)

[11]Dong Zushun,Dong Wencai.A simplified criterion and an analysis of some influence factors on longitudinal motion stability of Small Waterplane Area Twin-Hull ships[J].Shipbuilding of China,1994(4):36-48.(in Chinese)

[12]Dong Zushun,Dong Wencai.Analysis of some influence factors on seakeeping of Small Waterplane Area Twin Hull Ships(SWATH)[J].Journal of Naval Academy of Engineering,1995,1:7-15.(in Chinese)

[13]Liu Zhihua,Dong Wencai,Xiong Ying.Study on lines of lower hull of small-sized high-speed SWATH ship[J].Ship Engineering,2004,6:4-8.(in Chinese)

[14]Chen Rui,Xie Wei.Prediction of SWATH ship seakeeping performance[J].Chinese Journal of Ship Research,2008,3(1):9-12.(in Chinese)

[15]Lin Zheng.Research on the motions in wave and stability of the motions for Swath ship[D].Wuhan:Wuhan University of Technology,2009.(in Chinese)

[16]Mao Xiaofei.Numerical study of the motion response prediction of SWATH ship in waves[J].Ship&Ocean Engineering,2006(4):13-15.(in Chinese)

[17]Wu Jie,Gu Jiayang,Guan Yifeng,et al.Prediction of SWATH research ship seakeeping performance based on the Rankine source method[J].Journal of Jiangsu University of Science and Technology(Natural Science Edition),2015,29(2):103-107.(in Chinese)

[18]Qian P,Yi H,Li Y.Numerical and experimental studies on hydrodynamic performance of a small-waterplane-area-twinhull(SWATH)vehicle with inclined struts[J].Ocean Engineering,2015,96:181-191.

[19]Yao C B,Dong W C.A fast integration method for translating-pulsating source Green function in Bessho form[J].Journal of Zhejiang University-A,2014,15(2):108-119.

[20]Lee C M,Murray L O.Experimental investigation of hydrodynamic coefficients of a small-waterplane area,twin-hull model[R].NSRDC Report SPD 747-01,1977.