基于Floyd算法对蔬菜运送方案的最优分析

王 妍 朱家明 王欣宇 张一鸣

（1.安徽财经大学统计与应用数学学院，安徽 蚌埠233030；2.安徽财经大学金融学院，安徽 蚌埠233030）

针对我国居民副食品短缺问题，农业部于1988年提出建设“菜篮子工程”。其中，蔬菜作为“菜篮子工程”中的主要产品，如何合理分配备受关注。对于一些中小城市，蔬菜种植采取以郊区和农区种植为主，结合政府补贴的方式来保障城区蔬菜的供应[1]。随着信息与物流技术的日益完善，不断优化城市的蔬菜运输方案，既能提高城区蔬菜供应的数量和质量，也能带动郊区和农区菜农种植蔬菜的积极性。本文试图利用Floyd算法对各蔬菜种植基地、销售点最短距离进行求解，为提高城市蔬菜物流的综合经济效益提供理论基础。

1.数据来源与模型假设

数据来源于2017年安徽财经大学暑期数学建模模拟题1中附件一：蔬菜种植基地日供应量；附件二：蔬菜销售点日需求量及短缺补偿；附件三：道路交通情况及距离；附件四：蔬菜销售点对每种蔬菜的需求量。

JG市的人口近90万，该市在郊区和农区建立了8个蔬菜种植基地，承担全市居民的蔬菜供应任务，每天将蔬菜运送到市区的35个蔬菜销售点。市区有15个主要交通路口，在蔬菜运送的过程中从蔬菜种植基地可以途径这些交通路口再到达蔬菜销售点。如果蔬菜销售点的需求量不能满足，则市政府要给予一定的短缺补偿。同时，市政府还按照蔬菜种植基地供应蔬菜的数量以及路程，发放相应的运费补贴，以此提高蔬菜种植的积极性，运费补贴标准为0.04元/吨.公里。

针对研究问题，提出以下几点假设：（1）假设运输途中不存在蔬菜的损耗，且蔬菜只来源于8个基地，不考虑其他来源；（2）假设每一辆车只运往一个销售点，到达该销售点后即折返，不再前往下一个销售点，且不算折返距离；（3）假设只考虑运输补贴费用和短缺补偿费用，不考虑装卸费用等其他费用。

2.研究思路

为了便于直观地反应各蔬菜种植基地、销售站点和路口之间的距离关系，利用Graphviz绘图软件得到蔬菜运输路线的平面图。构造邻接矩阵表示各基地、路口及销售点的相对位置信息，利用图论中的Floyd算法，使用MATLAB软件求出各地点的最短距离，最后利用线性约束思想，通过LINGO软件编程，求得结果。

3.Graphviz软件中创建基地销售点平面图

根据附件三 （道路交通情况及距离）中的数据，为便于在平面图上更好地显示，首先将数据整合成统一形式，将8个蔬菜种植基地命名为Base1~Base8，15个交通路口命名为 Intersec1~Intersec15，35个销售站点命名为Stand1~Stand35。

利用 Graphviz画出平面图，见图 1（蓝色点表示蔬菜种植基地，黄色点表示路口，红色点表示蔬菜销售点）。部分程序如下。

graph test{

//基地着色蓝

base1[color=blue, style=filled];

base2[color=blue, style=filled];

base3[color=blue, style=filled];

//站点着色红

stand1[color=red, style=filled];

stand2[color=red, style=filled];

stand3[color=red, style=filled];

//路口着色黄

intersec1[color=yellow, style=filled];

intersec2[color=yellow, style=filled];

intersec3[color=yellow, style=filled];

base1——stand4[lebel="14"];

base1——stand14[lebel="16"];

base1——intersec3[lebel="16"];

图1 蔬菜运输平面图

4.模型的建立与求解

4.1 模型Ⅰ：最短距离模型

4.1.1 Floyd算法简介

A0为邻接矩阵，递推产生一个矩阵序列A0，A1，…，AK，…An，其中 AK(i,j)表示顶点 Vi到 Vj的路径上所经过的顶点序号不大于K的最短路径的长度。迭代公式为：

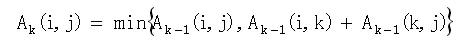
当k=n时，An即是各顶点之间的最短路长度。

4.1 .2模型的求解

由于种植基地、路口和销售站一共为58个基点，根据Floyd算法，建立58×58的网络权矩阵，其中D[i][j]表示蔬菜种植基地到销售点之间的最短距离。

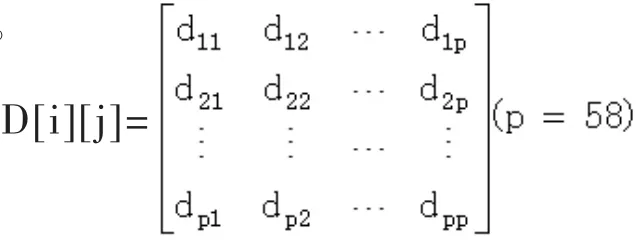
利用MATLAB[2]对相关数据进行迭代，得到种植基地与销售站的最小距离矩阵，具体数据详见表1，bi表示蔬菜种植基地，ij表示蔬菜销售点。

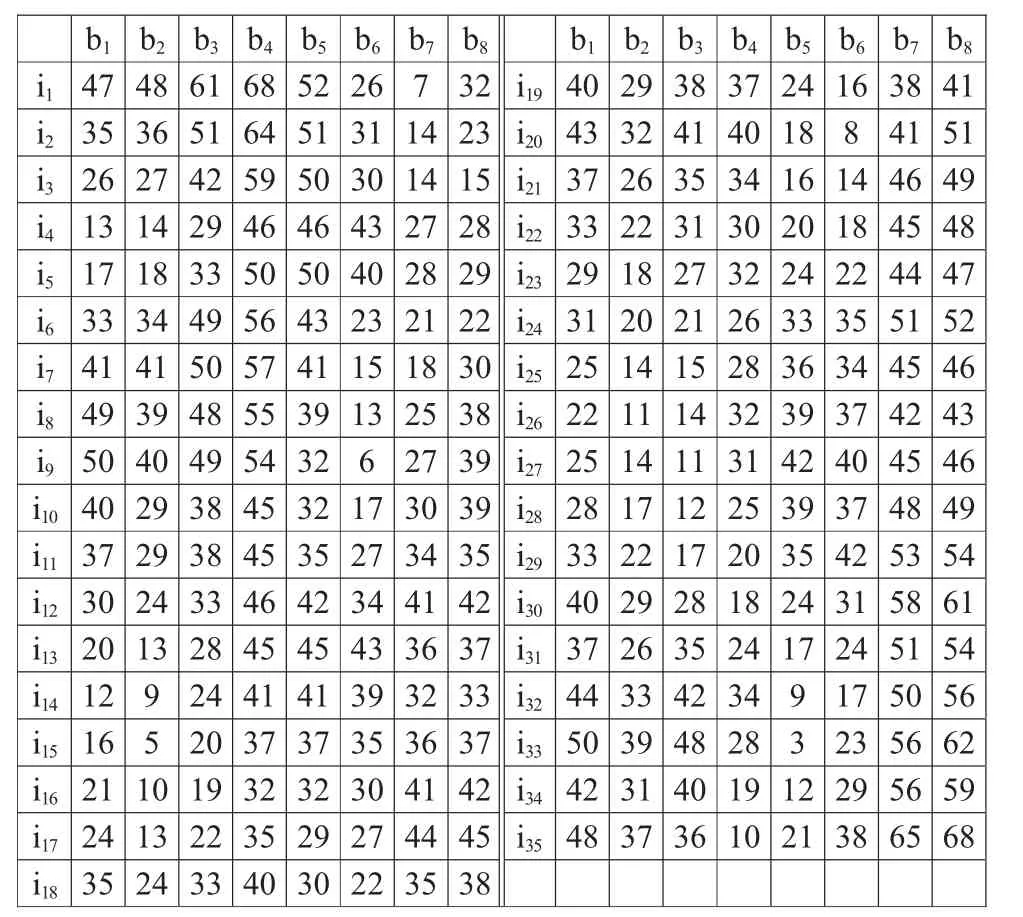
表1 种植基地与销售点之间的最小距离（单位：km）

4.2 模型Ⅱ：线性规划模型

4.2.1 建模准备

下表2表示各种植基地每日的蔬菜供应量，表3表示各蔬菜销售点的日需求量和短缺补偿。

表2 蔬菜种植基地的日供应量（吨/天）

表3 蔬菜销售点日需求量（吨/天）和短缺补偿（元/吨.天）

根据表2和表3中的数据，我们可以直观地看出，日供应总量ΣT=270（吨/天）小于日需求总量ΣM=360.1（吨/天），所以可以利用线性规划问题来求解。在问题一中分为两个约束条件，下面对两个约束条件分别进行求解。

（1）短缺补偿和运费补贴最小。

设在蔬菜运输中总的费用为F，政府运输费用补贴为 F1，短缺补偿为 F2，F＝F1＋F2，其中，F1满足：

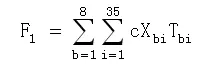
b,i分别表示生产基地与销售站，Xbi表示生产基地到销售点的距离，Xbi表示各生产基地对销售点的蔬菜供给量，C表示每吨每公里运费补贴标准。

上式中的1i表示每个销售点每吨每天的短缺补偿，Mi表示销售点i的蔬菜日需求量。

约束条件有：基地b对销售点的日供应量不大于基地b的日产量；基地对销售点i的日供应量不大于销售点i的日需求量；基地b对销售点i的日供应量不小于0。

建立线性规划模型[3]如下：

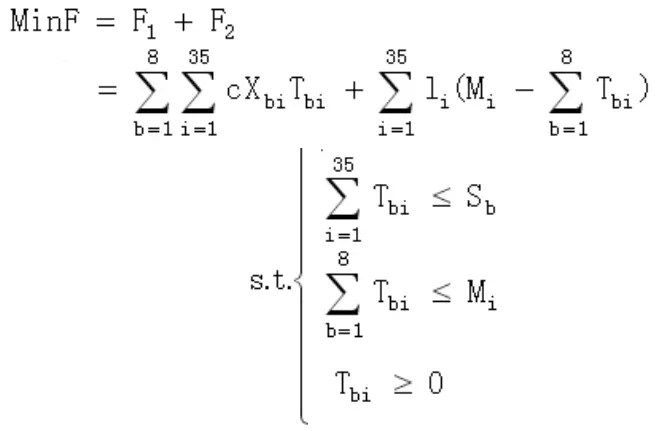
上式中Sb表示基地b的日产量。

代入已知数值，用LINGO求解[4]得到结果，鉴于文章篇幅，仅给出部分结果，见表4所示。

表4 蔬菜配送方案I（单位：吨）

代入短缺补偿和运费补贴的数值，我们可以计算得出，目标函数最小费用为42836.28元。

（2）短缺量不超过需求量的30%。

在此约束条件下，目标函数没有发生变化，建立线性规划模型[5]如下：

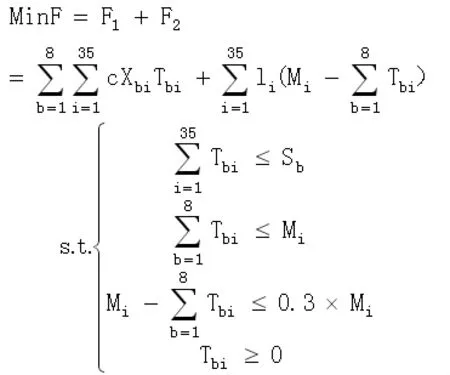
利用LINGO进行计算，得到计算结果如表5所示。由于文章篇幅限制，下表仅为部分结果。

LINGO编程程序如下：

model:

sets:

jd/1..8/:supply;

xsd/1..35/:need,compensation;

links(jd,xsd):d,x;

endsets

data:

c=0.04;

supply=40,45,30,38,29,35,25,28;

need=6.5,10.2,12,14.3,13,11,14,9.5,10,8.4

,10.5,7,8.5,12,11.6,12.5,13.6,9,7.3,10,12.7

,7.4,6.7,12.5,9.6,15,7.2,8.9,10.3,9,7.7,8,

11.4 ,12.1,10.7;

compensation=710,700,580,600,570,480,500,

610,440,705,610,630,590,490,570,460,530,

640,665,650,580,680,685,560,660,430,540,

620,630,680,695,690,560,520,500;

@ole('C:UsersSTUDesktopjieguo1_2.xlsx',x)=x;

enddata

min=c*@sum(links:d*x)+@sum(xsd(j):(need(j)-

@sum(jd(i):x(i,j)))*compensation(j));

@for(jd(i):@sum(xsd(j):x(i,j))=supply(i));

@for(xsd(j):@sum(jd(i):x(i,j))<=need(j));

@for(xsd(j):need(j)-@sum(jd(i):x(i,j))<=0.3*need(j));

End

表5 蔬菜配送方案 II（单位：吨）

代入短缺补偿和运费补贴的数值，我们可以计算得出，目标函数最小费用为50478.69元。

5.结论

本文针对具有现实意义的 “菜篮子工程”中蔬菜配送方案设计问题，运用MATLAB软件和LINGO软件编程，操作简单，效果较好。综合改进的Floyd算法，按照每一步求解需要灵活选取数据，循序渐进，逐步完善，加快了迭代速度，大大减少运行时间，较好地解决了任意两点间最短距离问题。线性规划模型操作简便，使用灵活，运用范围较大，便于推广。

[1]王一鸣,韩曙.“菜篮子工程”政策的理论与实践[J].上海财税,1994(6):7-10.

[2]周炳生.Floyd算法的一个通用程序及在图论中的应用[J].杭州应用工程技术学院学报,1999(3):1-9.

[3]闵欣.线性规划在利润最大化和成本最小化问题中的应用[J].黑龙江科技信息,2013(21):125-126.

[4]张银灵.Lingo软件在运输问题中的应用研究[J].中国商界(下半月),2010(10):205.

[5]姜启源,谢金星,叶俊.数学模型:第 3版[M].北京:高等教育出版社,2007.