索赔额服从混合指数分布的一类期望折现罚金函数

邵晶晶，王秀莲，邹 华

（天津师范大学数学科学学院，天津 300387）

经典风险模型中保险公司的盈余过程可表示为

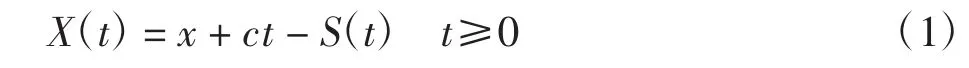
期望折现罚金函数定义为

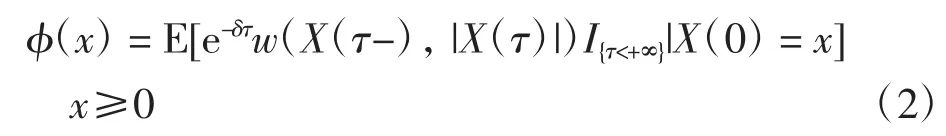
其中：δ≥0为折现因子；τ为破产发生的时刻；X（τ-）为破产时刻之前的盈余；|X（τ）|为破产时的赤字；I{·}为示性函数；w（X（τ-），|X（τ）|）是一个罚金函数，依赖于破产前的盈余和破产时的赤字，一般设w（·，·）为在[0，+∞）×[0，+∞）上的非负可测函数.

针对不同的情况，罚金函数可以选择不同的形式，如文献[1]研究了罚金函数为指数形式的期望折现罚金函数；文献[2]研究了罚金函数为w（U（T））的期望折现罚金函数.通常情况下，当保险公司盈余首次为负值时，即认为公司破产[3].对于这种破产情形，相关文献得到了很多有价值的结果.文献[4]研究了索赔时间间隔为相位分布的期望折现罚金函数.文献[5]研究了带干扰的有2个泊松过程的破产概率.文献[6]研究了索赔时间间隔为相位分布的破产概率.在保险公司的实际运营过程中，当公司资产为负值时，不一定会发生破产，公司可以通过采取某些措施解决临时的资金问题，直到公司发生实质破产.实质破产由Albrecher等[7]于2011年首次提出.关于实质破产模型，文献[8]研究了索赔额服从指数分布的破产概率，文献[9]研究了索赔时间间隔为混合指数分布的期望折现罚金函数.

本文在罚金函数仅与赤字有关的条件下，考虑索赔额服从混合指数分布时常数实质破产率情况下的期望折现罚金函数.

1 期望折现罚金函数的积分微分方程

在实质破产情况下，由于公司的盈余可以为负值，因此考虑罚金函数仅与赤字有关，定义期望折现罚金函数为

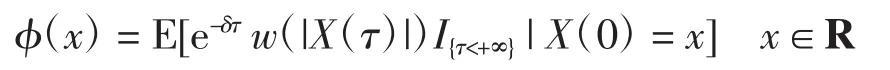
其中τ为实质破产发生的时刻.

考虑在很小的时间区间（0，h）内，以是否有索赔发生或发生实质性破产为条件，时间为h时，第一次索赔或实质破产同时发生的概率是高阶无穷小.因此由全概率公式有

在式（3）中令 x=0，并令 h→0，可得 φ（x）在 x=0处右连续，在式（4）中令 x=-ch，并令 h→0，有 φ（x）在x=0处左连续，即

因此∀x∈R，φ（x）连续.式（3）和式（4）关于 h 求导，并令h→0，有

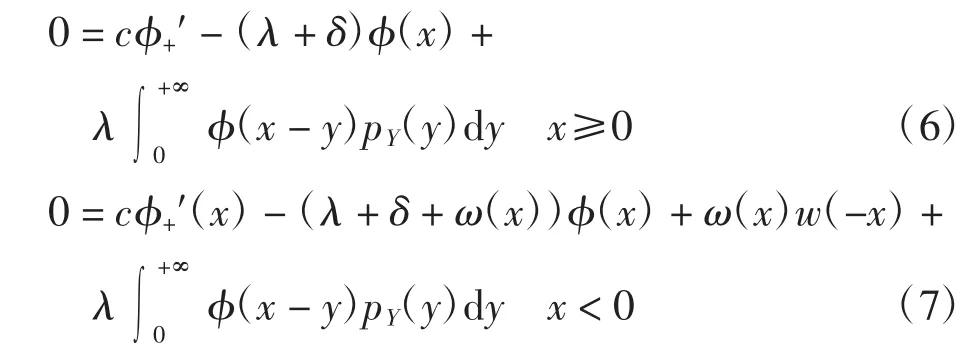
其中为 φ（x）的右导数.用 x-ch 替换式（3）和式（4）中的x，并关于h求导，再令h→0，有

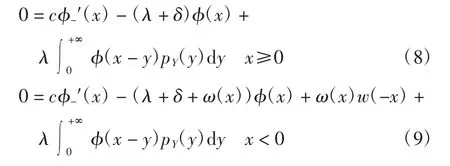
其中为 φ（x）的左导数.

由φ（x）的连续性，比较式（6）和式（8）可得，x＞0存在，比较式（7）和式（9）可得，x＜0存在.

由式（5）、式（6）和式（9）可得

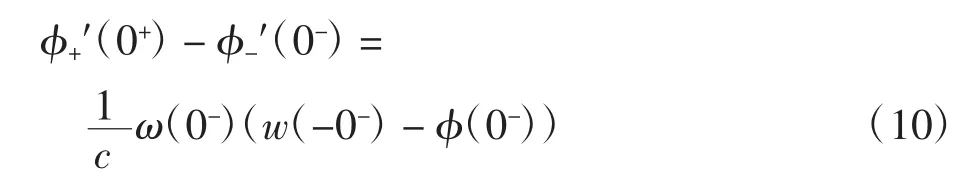
若令ω（0-）=0，可得在x=0连续.定义

则式（8）和式（9）可变成

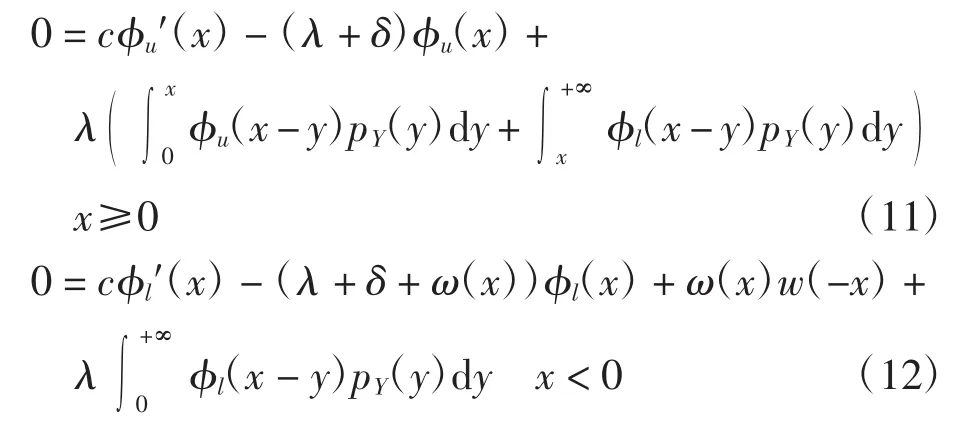
并有和·（w（-0-）- φ（0-））.

2 期望罚金函数的显示表达式

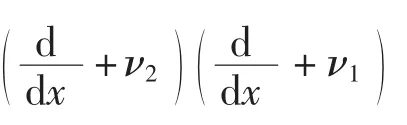
可得

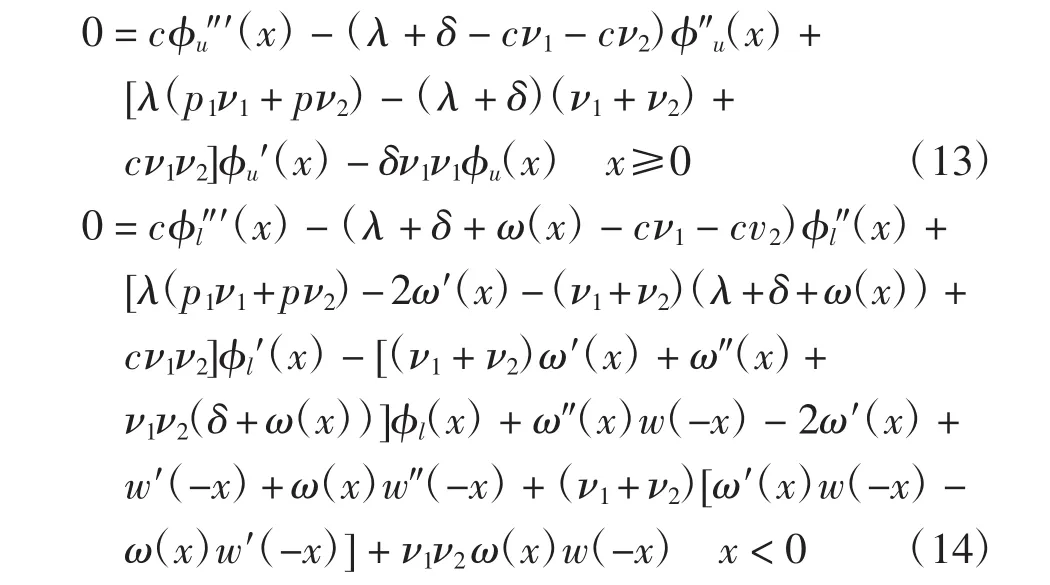
方程（13）的解为

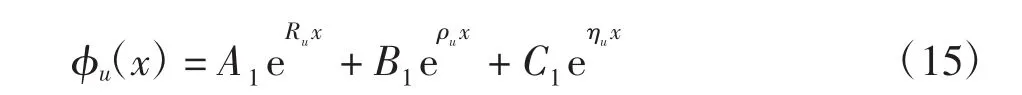
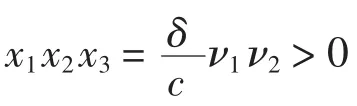
对于一般函数ω（x），方程（14）是一个变系数微分方程.下面设破产率函数ω（x）=ωc·I{x＜0}（ωc＞0），w（-x）=1，则有

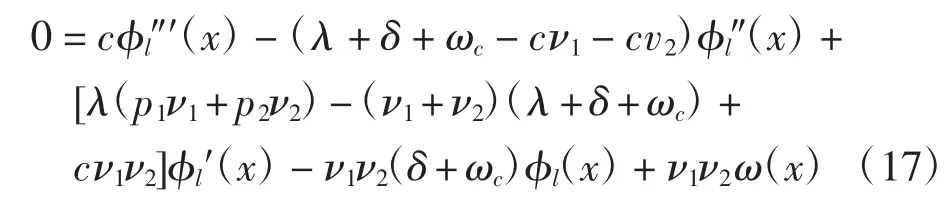
方程（17）对应的齐次方程的特征方程为

设方程（17）的解为

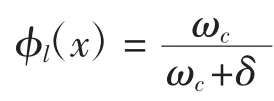
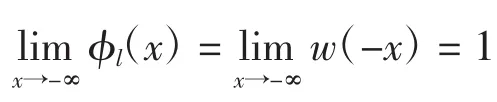
将φu（x）和φl（x）代入式（13）和式（14），比较项和项的系数，得

由连续条件可得

由式（19）～式（21）可得

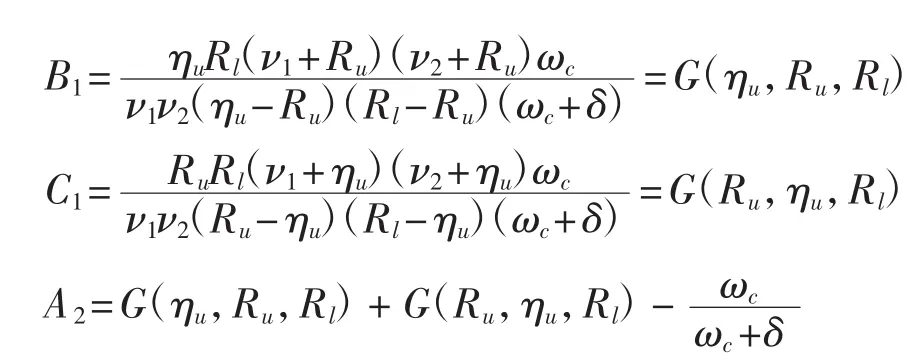
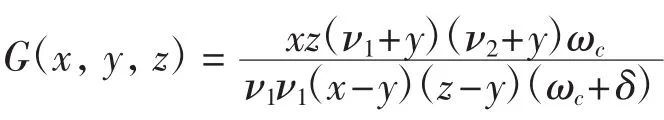
[1]ALBRECHER H，CHEUNG C K，THONHAUSER S.Randomized observation periods for the compound Possion risk model：The discounted penalty function[J].Scandinavian Actuarial Journal，2013，13（6）：424-452.

[2]GERBER H U，SHIU E S W，YANG H L.The Omega model：From bankruptcy to occupation time in the red[J].European Actuarial Journal，2012，2（2）：259-272.

[3]GERBERHU，SHIU E S W.On the time value of ruin[J].North American Actuarial Journal，1998，2（1）：48-72.

[4]SONG M，MENG Q B，WU R，et al.The Gerber-Shiu discounted penalty function in the risk process with phase-type interclaim times[J].Applied Mathematics and Computation，2010，216（2）：523-531.

[5]DONGYH，ZHANGHJ.Ruinprobabilityinriskmodelwithtwo Poisson processes by diffusion[J].Mathematical Theory and Application，2003，23（1）：98-101.

[6]GERBERHU，SHIUESW.Thetimevalueofruin in a Sparre Andersen Model[J].North American Actuarial Journal，2005，9（2）：49-69.

[7]ALBRECHER H，GERBER H U，SHIU E S W.The optimal dividend barrier in the Gamma-Omega model[J].European Actuarial Journal，2011，1（1）：43-56.

[8]ALBRECHER H，LAUTSCHAM V.From ruin to bankruptcy for compound Poisson surplus processes[J].Astin Bulletin，2013，43（2）：213-243.

[9]李野默，王秀莲.复合泊松风险模型中观察间隔为混合指数分布的贴现罚金函数[J].天津师范大学学报（自然科学版），2015，35（2）：17-20.LI Y M，WANG X L.Discounted penalty function of compound Poisson risk modelwhen observation intervalbeing mixed exponential distribution[J].Journal of Tianjin Normal University（Natural Science Edition），2015，35（2）：17-20（in Chinese）.