一种降低OFDM/OQAM系统峰均比的C-OSLM联合算法
靳寒阳 ,王 波 ,李燕龙
1.桂林电子科技大学 认知无线电与信息处理教育重点实验室,广西 桂林 541004
2.中国电子科技集团公司第五十四研究所 通信网信息传输与分发技术重点实验室,石家庄 050081
1 引言
正交频分复用/交错正交幅度调制(Orthogonal Frequency Division Multiplexing/OffsetQuadrature Amplitude Modulation,OFDM/OQAM)技术在近年来受到学术界广泛的重视[1-3],成为了5GNOW[4]、PHYDYAS以及METIS[5]等欧盟项目的重点研究内容,并被我国IMT-2020(5G)推进组纳入5G物理层调制波形的主要候选方案之一。通过引入具有良好时频聚焦特性的滤波器,OFDM/OQAM系统能够有效抵抗载波间干扰(Inter-Carrier Interference,ICI)和码间串扰(Inter-Symbol Interference,ISI)[6],进而避免了循环前缀(Cyclic Prefix,CP)[7-8]的使用,提高了频谱利用率。
但作为一种多载波调制方式,OFDM/OQAM系统也会由于多个子信道叠加产生较大的峰值,导致峰均比(Peak-to-Average Power Ratio,PAPR)较高。在系统的硬件实现过程中,这一问题将增加对功率放大器线性范围的要求,使得系统实现成本剧增,也降低了放大器的工作效率。因此,降低OFDM/OQAM系统的峰均比是其工程应用的一个重要问题。
在传统OFDM系统中,从是否会对原信号带来失真的角度可将峰均比抑制方法分为有失真方法和无失真方法。信号有失真方法的典型代表为限幅(Clipping),压缩扩展变换(Companding)。信号无失真方法有编码(Coding)、选择映射(Selective Mapping,SLM)、部分传输序列(Partial Transmit Sequence,PTS)以及预留子载波(Tone Reservation,TR)等。
上述方法中,Clipping可直接应用于OFDM/OQAM系统中,但会为系统带来信号失真,影响误码性能[9]。而无失真方法大多要求其应用场景下的数据符号之间具有独立性,由于OFDM/OQAM系统中存在“符号重叠”这一现象,这些方法不能被直接应用于OFDM/OQAM。针对符号重叠的问题,文献[10]对SLM进行改进,在为当前符号筛选码字时,增加对所有与之重叠符号的考虑,提出了重叠选择映射法(Overlapped Selective Mapping,OSLM);文献[11]引入一种滑动窗口结构,对OFDM下的预留子载波法进行了改进;文献[12]通过对OFDM/OQAM系统中的符号进行分块处理,提出一种分段-部分传输序列法(Segmental Partial Transmit Sequence,S-PTS)法;文献[13]将符号分块后进行动态联合优化,提出一种基于PTS方法的多块联合优化(Multi-Block Joint Optimization,MBJO)算法;文献[14]针对OSLM计算复杂度高的问题,提出一种改进型OSLM算法(Improved Overlapped Selective Mapping,IOSLM)。
上述针对符号重叠问题提出的算法均对传统算法进行了改进,使之适用于OFDM/OQAM的峰均比抑制。
然而,其中预留子载波类方法需要预留额外的子载波用于峰值抵消,占用了一定的频带资源。对于PTS与SLM类改进算法,SLM类算法不需要PTS中特定的优化模块来计算选出最优码字,实现较为简单。文献[14]中所提出的IOSLM算法针对OSLM算法的复杂度问题进行了优化,但由于增加了对重叠符号的考虑,IOSLM算法计算量仍高于OFDM中SLM算法一倍以上。而在算法实际应用过程中,虽然算法性能会随码字组数的翻倍有逐步提升,但此过程中算法性能增益会逐渐减小,系统的计算量也会倍增。
文献[15-17]指出,在OFDM系统下,Clipping与SLM的联合算法可以显著提升PAPR抑制效果。然而,目前为止还没有基于OFDM/OQAM系统对二者联合算法的相关研究。
本文基于OFDM/OQAM系统提出限幅-重叠选择映射(Clipping-OSLM,C-OSLM)联合算法。并通过选择算法参数的最优值,使C-OSLM在引入Clipping的同时保证系统的误码性能,以极小的计算复杂度为代价,大幅降低OFDM/OQAM系统峰均比。
2 OFDM/OQAM的系统模型及PAPR
2.1 OFDM/OQAM系统模型
设子载波数为N,符号数为M,则OFDM/OQAM系统的基带等效发送信号可表示为:

am,n是第m个符号中第n个子载波上发送的实值数据符号,T为符号周期,h(t)为原型滤波器的冲击响应。本文采用长度为4T的各项同性正交变换函数[10,14,18](Isotropic Orthogonal Transform Algorithm,IOTA)滤波器,相位偏移为时-频格点坐标为(m,n)处的基函数,由于OFDM/OQAM系统在实数域严格正交,系统满足如下内积运算式:

其中为内积运算与取实操作,当m=m0时,δm,m0=1,否则δm,m0=0。
OFDM/OQAM的系统框图如图1所示。在发送端,数据经串并变换后,将每个符号分别取实部与虚部放置上下两路,再进行相位偏置、快速逆傅里叶变换,之后分别经过两个彼此在时域上相差半个符号周期的滤波器,最终将上下两路信号数据叠加,经并串转换传输至信道。
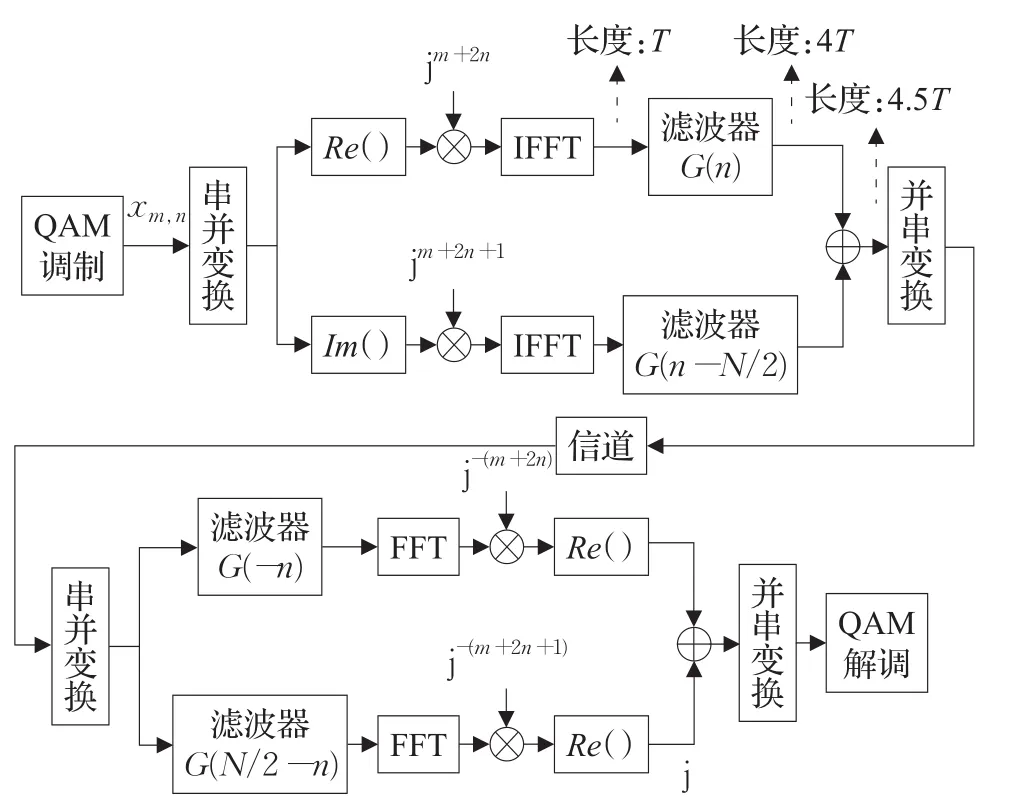
图1 OFDM/OQAM系统实现框图
符号重叠情况如图2所示,以图中第5个符号为例,每个当前符号会受到前4个符号的重叠影响。这是由于OFDM/OQAM系统中采用的滤波器长度为4T,符号在经过滤波器后,其长度从T变为4T。而上下两路滤波器的不同导致了两路数据间存在半个符号周期的时域间隔,故每个符号在经过OFDM/OQAM系统发射端的整个调制过程后,其长度由T变为了4.5T。又由于符号周期固定(符号周期为T),经过OFDM/OQAM调制后的每个当前符号将受到前4个符号之间的重叠影响。
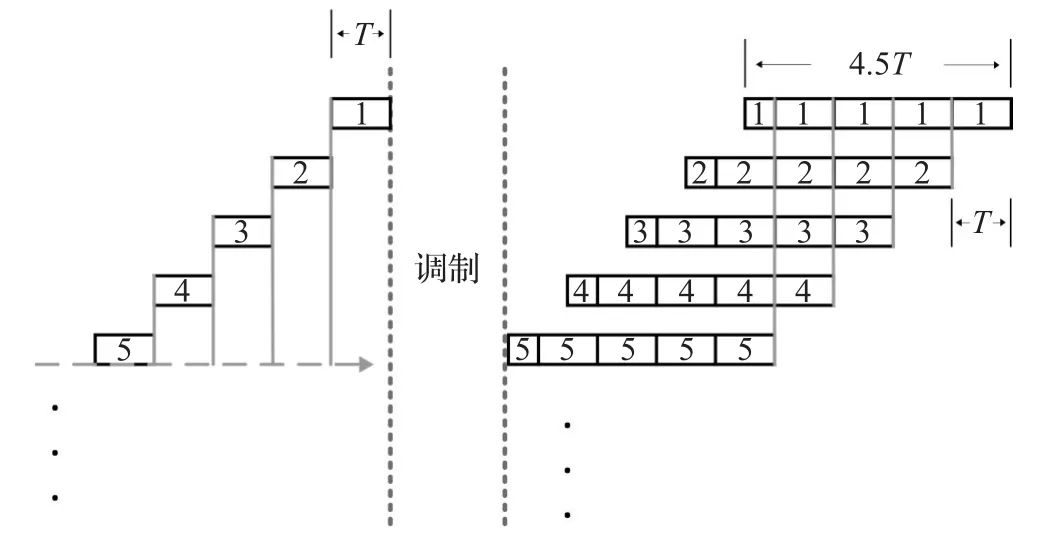
图2 OFDM/OQAM系统符号重叠示意图
这导致要求符号间具有独立性的SLM无法直接应用于OFDM/OQAM系统,针对此问题,在使用SLM在为每个当前符号筛选码字时必须附加对与之重叠符号的考虑。
2.2 OFDM/OQAM的PAPR
在OFDM系统中,PAPR的定义为时域信号功率的峰值与均值之比,基带信号的PAPR表示为:

虽然OFDM/OQAM系统中符号间存在重叠影响,但相关文献[19-20]指出,OFDM/OQAM系统与OFDM系统在一个符号周期内均传输一个完整实值符号。对于OFDM/OQAM系统,可使用与OFDM系统下表达式相同的互补累积分布函数(Complementary Cumulative Distribution Function,CCDF)来作为衡量PAPR的方法。CCDF通常以PAPR大于某门限值γ(或PAPR0)的概率来表示:
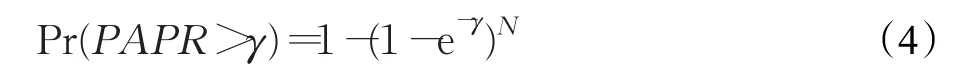
3 C-OSLM峰均比抑制算法
3.1 SLM与Clipping
SLM[21](选择映射)的原理是:在调制出频域数据并进行串并转换之后,产生U组矢量元素幅值均为1的相位矢量(也称作U组码字)。分别与每个符号进行点乘、产生U组备选信号,从U组备选信号中选择一组PAPR最小的作为最终的传输方案,并在接收端变换至频域之后将与每个符号对应点乘的码字去除。码字元素形式为=α∈[0,2π);n=1,2,…,N;u=1,2,…,U 。
Clipping(限幅)的原理为:设定阈值,将时域信号幅值与之进行对比,如超过阈值则保持信号辐角不变,将幅值强制置为阈值,如不超过阈值则不做处理。经过限幅操作之后的时域信号可表示为:

其中A=CR⋅Aav为限幅阈值,CR为限幅率(Clipping Rate),Aav为符号内每个频点数据幅值的均值,ϕ(t)代表原信号辐角。
3.2 C-OSLM
SLM无法直接应用于OFDM/OQAM系统,虽然在增加了对与当前符号重叠的前4个符号的考虑后,以OSLM的形式应用于OFDM/OQAM系统中。但对于“符号重叠”影响的考虑增加了码字选择的约束,降低了码字筛选的自由度,从而使OSLM算法的PAPR抑制性能不甚理想。文献[14]指出,由于OFDM/OQAM系统中的滤波器通常具有良好的时频聚焦特性,滤波器的能量主要集中在中间部分。这导致与当前符号发生重叠的符号数虽为4个,但对当前符号数据有着实质性影响的仅为距离当前符号最近的一个符号。并基于此理论提出IOSLM算法,将筛选码字时考虑的重叠符号个数从4改为1,在减小计算复杂度的同时,一定程度上增加了码字筛选的自由度,提升了算法性能。
在OFDM系统下,Clipping与SLM有3种结合方式[15-17]。本文将IOSLM算法与Clipping结合,对应的OFDM/OQAM系统下IOSLM算法与Clipping 3种结合方式如图3所示(方案A、B、C)。

图3 C-OSLM算法结构框图
3种方案不同之处在于插入限幅操作的位置不同:
方案A:将限幅操作插入至OFDM/OQAM系统的“频-时”变换过程之后、码字选择之前,“频-时”变换过程指数据由频域转换至时域的整个过程,其中包括实虚分路、相位偏移、IFFT、经过滤波器以及实虚路相叠加一系列操作;
方案B:将限幅操作插入至码字选择之后、进入信道之前;
方案C:将限幅操作插入至串并变换之后、点乘码字之前。
由于限幅的操作对象为时域数据。OFDM系统中数据由频域转换至时域仅需IFFT即可完成,而OFDM/OQAM系统中频域数据则需经过实虚分路、相位偏移、IFFT、经过滤波器以及实虚路相叠加等一系列过程。因此方案C极高的复杂度决定了其并不适用于OFDM/OQAM系统,本文的C-OSLM联合算法采用方案A与方案B两种方案来对OFDM/OQAM系统的峰均比抑制进行研究。其实施过程可用图4流程图表示。

图4 C-OSLM算法流程图
算法具体操作包括如下步骤:
步骤1初始化。产生U组相位矢量(码字)用于与每个符号进行点乘。每组码字长度为N,码字元素表示为,i=1,2,…,U,与码字点乘后的实值数据表示为m=1,2,…,M;n=1,2,…,N,每个符号对应的最优码字为ik,k=1,2,…,U。
步骤2构建第一个符号。任取U组码字中的一组作为第一个符号的最优码字[10](例如取第一组,记i1=1),将第一个符号与其最优码字的点乘结果A1存储下来:

步骤3构建第k个符号。对于时隙Ik=[kT,(k+1)T],k≥2,考虑如下矩阵:
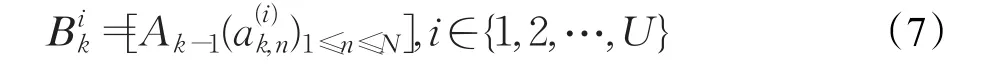
步骤4“频-时”变换。将步骤3中U个N行2列的矩阵分别经过“频-时”变换过程,得到U组时域形式数据。
对于方案A与方案B,二者从步骤5开始有所不同。
对于方案A:
步骤5限幅并计算数据的PAPR。对时域数据进行如式(5)的限幅操作,并进行PAPR计算。此处由于每个符号的长度为4T,故PAPR计算方式为:

步骤6码字筛选。按如下规则选出第k个符号的最优码字组数:

并将umin记为ik。
步骤7传输至信道。对于第k+1个符号,重复步骤3~6,选出每个符号对应的最优码字,并将所有频域符号与其对应的码字点乘后,经“频-时”变换至时域,与ik一同传输至信道。
对于方案B:
步骤5计算数据的PAPR并选择最优码字。按照式(8)进行PAPR的计算,再按式(9)进行最优码字的选择并记录、存储ik。对于第k+1个符号,重复步骤3~5,选出每一个符号的最优码字,并将所有频域符号与其对应的最优码字点乘后,经“频-时”变换至时域。
步骤6限幅。按照式(5)规则对所有时域信号进行限幅操作。
步骤7传输至信道。将经过限幅的时域数据与ik一同传输至信道。
4 仿真结果分析
本研究中OFDM/OQAM系统采用4进制正交幅度调制(Quadrature Amplitude Modulation,QAM)调制方式,符号数为1 000,子载波数为128,采用滤波器长度为4T的IOTA滤波器,使用高斯信道,具体参数设置参见表1。
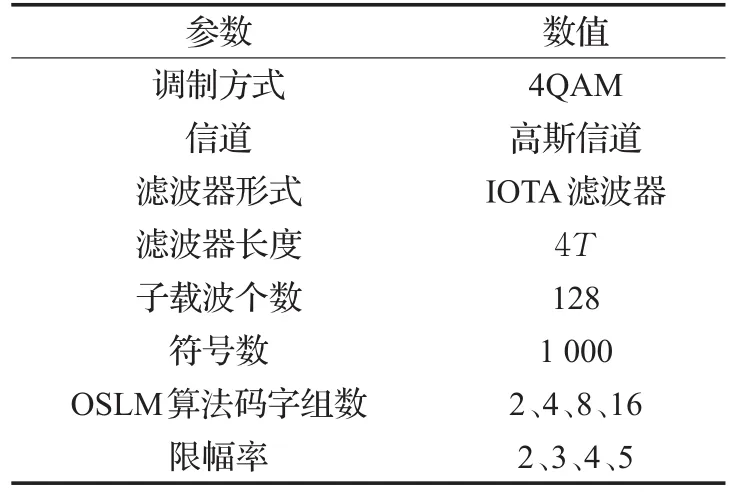
表1 OFDM/OQAM系统参数
IOSLM作为概率类算法,不影响系统误码率,而Clipping会为系统带来非线性畸变。二者结合后误码性能损失只与Clipping中CR的大小有关,与Clipping插入的位置无关。故方案A与B的误码率曲线重合,可用其一误码率曲线代替二者。
本文首先研究C-OSLM算法的误码性能随Clipping中CR的变化情况,以保证通信系统可靠性为目的选出CR的最优值。进一步,用CCDF曲线作为衡量C-OSLM算法峰均比抑制性能的方式,与单独使用Clipping、IOSLM法的CCDF进行对比研究。
图5为无PAPR抑制、OSLM、IOSLM算法与几种不同限幅率的C-OSLM算法的误码性能对比。可以看出,OSLM与IOSLM误码曲线与无PAPR抑制的曲线重合(这是由于二者没有引入限幅,均属于无失真类算法)。而对于C-OSLM算法,CR取值越小,C-OSLM误码率曲线与IOSLM相比偏差越大。这是因为在Clipping中,虽然PAPR抑制效果会随CR的减小逐渐提升,但与此同时Clipping为系统带来的非线性失真会愈发严重。此外,由图5可以看到,当CR为5时,误码率曲线与无失真曲线几乎重合。因此,为保证系统误码性能,CR的取值应不小于5。

图5 各算法误码率比较
图6为IOSLM算法与OSLM算法CCDF曲线对比图。可以看出:(1)IOSLM算法在每一种码字数情况下比OSLM算法均有一定性能提升;(2)对于IOSLM算法,设U=1(码字数为1)对应筛选码字所需的计算量为Χ,显然U=2与U=4、U=8、U=16对应的计算量为2Χ 、4Χ 、8Χ 、16Χ ,而从图6可知,U=2与U=4两种码字情况下,PAPR峰值(即曲线与横轴交点处横坐标)抑制性能随码字数翻倍的增益分别为0.8 dB、0.6 dB,对应增加的计算量为 4Χ-2Χ=2Χ 、8Χ-4Χ=4Χ 。而U=8情况下,随码字数增倍(变为U=16)所带来的PAPR峰值抑制性能增益仅为0.4 dB,却为系统增加了16Χ-8Χ=8Χ的计算量。

图6 IOSLM与OSLM算法的CCDF比较
所以,考虑到通信系统可靠性(误码性能)以及实现成本、计算复杂度,本文以CR=5,U=8为例,对C-OSLM算法的PAPR抑制性能进行研究。
图7为CR=5,U=8的C-OSLM算法与单独应用Clipping、IOSLM算法的CCDF曲线对比图。为更准确地描述C-OSLM的性能,本文将纵轴概率为10-1.65~100范围内定义为“高概率区域”,10-3~10-1.65范围内定义为“低概率区域”。从图7可以看出:

图7 C-OSLM与Clipping、IOSLM算法的CCDF比较
(1)Clipping与IOSLM的对比:IOSLM在高概率区域的PAPR抑制性能优于Clipping,而Clipping在低概率区域表现更为出色。这是由于Clipping的思想是设定门限值,对超过门限值的信号进行“削砍”,此类算法对改善系统PAPR的峰值(即CCDF曲线与横轴的交点)极为有效,曲线通常会在某个PAPR0值处出现陡降;而IOSLM算法属于概率类算法,其思想是通过增加备选信号数量来以概率降低高PAPR符号出现的几率,此类算法长于改善系统整体峰均比,CCDF曲线通常会相对于无峰均比抑制曲线整体左移并且缓慢下降(如图6所示),而不会如Clipping出现陡降,对于系统PAPR峰值的改善不如Clipping高效。
(2)C-OSLM算法与Clipping对比:C-OSLM的方案A与方案B在各个概率区域内的PAPR抑制性能均优于Clipping。其中,在高概率区域,C-OSLM算法继承了SLM“改善系统整体PAPR”的特点,相对于Clipping有大幅性能提升(CCDF=10-0.5处的PAPR值降低了1 dB)。而在低概率区域,方案A与方案B也均优于Clipping,其中方案A在系统PAPR峰值(曲线与横轴交点)方面有0.2 dB的性能提升。
(3)C-OSLM与IOSLM算法对比:由于系统PAPR峰值决定了系统实现中对功率放大器线性范围上界的需求,所以CCDF曲线与横轴交点处横坐标的改变对于本研究“立足系统实现,为OFDM/OQAM系统的应用创造便利条件”这一目标意义更为重大。在此方面,C-OSLM算法继承了Clipping在低概率区域的优良性能。相比IOSLM算法,本文的C-OSLM算法的方案A与方案B均在PAPR峰值抑制方面有明显性能提升。其中,经过方案A抑制后的PAPR峰值相比IOSLM具有0.6 dB的减小,实现了对单独应用IOSLM“U=16”情况下PAPR抑制性能的超越(如图6所示,U=16的IOSLM算法PAPR峰值为7.3 dB,而对应图7中方案A为7.02 dB)。参照本文方案B步骤可知,相对U=16的IOSLM算法,U=8的C-OSLM减小了8倍两个符号共同经过“频时”变换过程的计算量,却仅增加了对最终时域数据进行Clipping这一过程。显然,C-OSLM以极小的计算量增加为代价,为IOSLM的PAPR峰值抑制性能带来了显著提升。
5 结束语
本文基于OFDM/OQAM系统对SLM与Clipping的联合算法进行了研究,提出了C-OSLM联合算法。研究结果表明该联合算法继承了两种算法各自优点,在各概率区域均有出色的PAPR抑制性能。在保证系统误码性能的前提下大幅降低了OFDM/OQAM系统峰均比。同时,由本文误码率曲线图5还可看出:在不同信噪比场景下分段设定C-OSLM的CR,可最大化发挥算法性能优势。
[1]Nam H,Choi M,Han S,et al.A new filter-bank multicarrier system with two prototype filters for QAM symbols transmission and reception[J].IEEE Transactions on Wireless Communications,2016,15(9):5998-6009.
[2]Perez-Neira A I,Caus M,Zakaria R,et al.MIMO signal processing in Offset-QAM based filter bank multicarrier systems[J].IEEE Transactions on Signal Processing,2016,64(21):5733-5762.
[3]Nissel R,Lerch M,Simko M,et al.Bit error probability for pilot-symbol-aided OFDM channel estimation in doublyselective channels[C]//2016 IEEE InternationalConference on Communications(ICC 2016),2016:1-6.
[4]Wunder G,Jung P,Kasparick M,et al.5GNOW:Nonorthogonal,asynchronous waveforms for future mobile applications[J].IEEE Communications Magazine,2014,52(2):97-105.
[5]Elayoubi S E,Fallgren M,Spapis P,et al.5G service requirements and operational use cases:Analysis and METIS II vision[C]//European Conference on Networks and Communications,2016:158-162.
[6]Dandach Y,Siohan P.Design method of OFDM/OQAM systems using a weighted time-frequency localization criterion[C]//European Signal Processing Conference,2010:70-74.
[7]Siohan P,Siclet C,Lacaille N.Analysis and design of OFDM/OQAM systems based on filterbank theory[J].IEEE Transactions on Signal Processing,2002,50(5):1170-1183.
[8]Chen D,Xia X G,Jiang T,et al.Properties and power spectral densities of cp based OQAM-OFDM systems[J].IEEE Transactions on Signal Processing,2015,63(14):3561-3575.
[9]Rahim M U,Stitz T H,Renfors M.Analysis of clippingbased PAPR-reduction in multicarrier systems[C]//IEEE Vehicular Technology Conference,2009:1-5.
[10]Skrzypczak A,Javaudin J P,Siohan P.Reduction of the peak-to-average power ratio for the OFDM/OQAM modulation[C]//IEEE Vehicular Technology Conference,Melbourne,Australia,2006:2018-2022.
[11]Lu S,Qu D,He Y.Sliding window tone reservation technique for the peak-to-average power ratio reduction of FBMC-OQAM signals[J].IEEE Wireless Communication Letters,2012,1(4):268-271.
[12]Ye C,Li Z,Jiang T,et al.PAPR reduction of OQAMOFDM signals using segmental PTS scheme with low complexity[J].IEEE Transactions on Broadcasting,2014,60(1):141-147.
[13]Qu D,Lu S,Jiang T.Multi-block joint optimization for the peak-to-average power ratio reduction of FBMCOQAM signals[J].IEEE Transactions on Signal Processing,2013,61(7):1605-1613.
[14]Cheng G,Li H,Dong B,et al.An improved selective mapping method for PAPR reduction in OFDM/OQAM system[J].Communications&Network,2013,5(3):53-56.
[15]More A P,Somani S B.The reduction of PAPR in OFDM systems using clipping and SLM method[C]//InternationalConferenceon Information Communication and Embedded Systems,2013:593-597.
[16]Gay M,Lampe A,Breiling M.A hybrid PAPR reduction scheme for OFDM using SLM with clipping at the transmitter,and sparse reconstruction at the receiver[C]//2014 IEEE 11th International Multi-Conference on Systems,Signals&Devices(SSD’14),2014:1-6.
[17]Sultan K,Ali H,Zhang Z.Joint SLM and modified clipping scheme for PAPR reduction[C]//International Bhurban Conference on Applied Sciences and Technology,2016:710-713.
[18]Chen D,Qu D,Jiang T,et al.Prototype filter optimization to minimize stopband energy with NPR constraint for filter bank multicarrier modulation systems[J].IEEE Transactions on Signal Processing,2013,61(1):159-169.
[19]Zhu X,Pan W,Li H,et al.Simplified approach to optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J].IEEE Transactions on Communications,2013,61(5):1891-1901.
[20]Skrzypczak B A,Siohan P,Javaudin J P.Analysis of the peak-to-average power ratio for OFDM/OQAM[C]//IEEE Workshop on Signal Processing Advance in Wireless Communications,2008:1-5.
[21]Bauml R W,Fischer R F H,Huber J B.Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping[J].Electronics Letters,1996,32(22):2056-2057.

