附有高程约束的卫星导航系统精度因子分析方法

徐健，武建锋



附有高程约束的卫星导航系统精度因子分析方法

徐健1,2,3,4，武建锋1,2,3,5

（1.中国科学院 国家授时中心，西安 710600；2. 中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3. 中国科学院 时间频率基准重点实验室，西安 710600；4. 中国科学院大学，北京 100049；5. 中国科学院大学 电子电气与通信工程学院，北京 101408）

高程约束定位方法是一种可以改善定位精度的方法，相对于最小二乘定位方法引入了地球椭圆约束方程。约束方程的引入改变了定位解算过程，使得来源于最小二乘定位方法的精度因子计算公式不再适用于新的方法。针对这一问题，从精度因子定义出发，结合高程约束定位方法原理，提出一种新的计算高程约束定位精度因子的方法。利用某一监测站的地球同步轨道卫星和倾斜地球同步轨道卫星数据，进行了两组精度因子值分析试验和一组定位试验，试验结果表明提出的高程约束定位方法精度因子的计算方法是正确的，高程约束定位方法的定位精度也远高于最小二乘方法。

高程约束；精度因子；最小二乘

0 引言

卫星星座布局是一个卫星导航系统的重要参数，在很大程度上决定了导航系统的定位精度[1]。因此，为了进一步提高区域定位精度，越来越多的卫星导航系统或增强系统采用地球同步轨道 （geosynchronous orbit，GEO）卫星。例如，我国的北斗一号卫星导航系统的星座全部由GEO卫星构成, 而且目前的星基增强系统（satellite-based augmentation system，SBAS）更是全部采用了GEO卫星；我国的北斗二号、日本准天顶卫星系统和印度区域卫星导航系统这三大区域性卫星导航系统，它们的星座就是由至少一组GEO卫星和另外一组倾斜地球同步轨道（inclined geosynchronous satellite orbit，IGSO）卫星构成，这种星座也被认为是区域性卫星导航系统星座的最佳构成[2-3]，另外，转发式卫星导航系统的星座通常也是由GEO卫星和IGSO卫星构成。

精度因子（dilution of precision，DOP）作为影响系统导航定位性能的因素之一，可以准确地描述可视卫星相对用户的几何分布对定位精度的影响[4]。为了提高系统定位精度，通常从降低卫星的测量误差和改善卫星的几何分布这两个方面入手。由于星座布局限制，GEO卫星和IGSO卫星构成的区域导航系统或转发式导航系统的位置精度因子（position dilution of precision，PDOP）和高程精度因子（vertical dilution of precision，VDOP）会比较大，水平位置精度因子（horizontal dilution of precision，HDOP）会相对较小。为了改善这个PDOP较大的问题，可采用高程约束定位方法，这种方法可以减少求解的未知数，增加信息冗余度，进而提高接收机在水平方向的定位精度。

前述的DOP的定义是基于最小二乘定位解算方法的，而高程约束定位方法引入了高程约束方程，相当于增加了一颗伪卫星，现有的DOP计算公式不适用于高程约束定位方法。因此，在DOP最初定义的框架下，推导高程约束定位方法的DOP计算公式成了一个问题。

本文基于高程约束定位方法原理，通过严谨的理论分析和公式推导，推导了高程约束定位方法的DOP计算公式。该方法首次提出了分析高程约束定位方法DOP值的方法，从理论的角度验证了高程约束定位方法相对最小二乘方法的改进。

1 高程约束定位方法

1.1 高程约束定位原理

高程约束定位方法一般通过气压测高获得接收机的高程，同时在定位解算部分引入一个椭球约束方程，相当于在地球中心位置附近增加了一颗虚拟卫星，极大地改善了卫星星座布局，几何精度因子明显变好[5-7]。这种情况下的观测方程如下：

图1 椭球约束面示意图

1.2 高程约束观测方程的解算

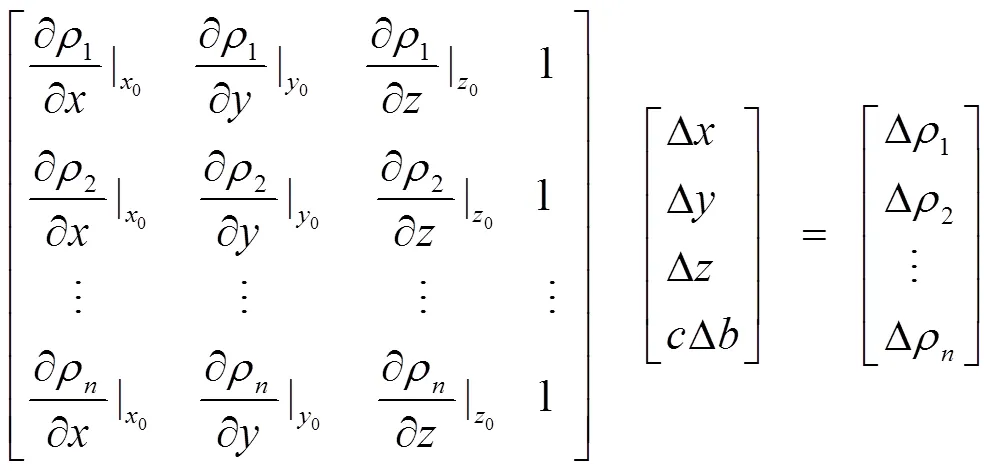
式（2）简化为

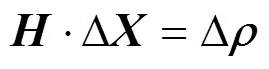
2 高程约束定位方法的DOP分析原理

高程约束定位方法是在最小二乘定位解算方法的基础上引入地球椭球约束方程，与添加辅助方程式的方法不同，地球椭球约束方程只是在观测方程组外作为一个约束条件存在，不直接参与定位解算，即两种方法的观测矩阵构成是一致的，高程约束定位方法带来的DOP改善并没有在观测矩阵中得到体现，原有的基于观测矩阵的DOP计算方式并不适用于高程约束定位方法，因此，需要在原有DOP计算方法基础上，不改变DOP的物理意义，推导适用于高程约束定位方法的DOP计算方法。

2.1 基于最小二乘的DOP计算方法

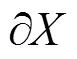
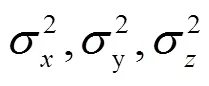
基于以上分析，定义了一下精度因子，式（6）中，GDOP为几何精度因子，PDOP为位置精度因子，TDOP为钟差精度因子：

为了定义水平方向和高程方向上的精度因子，我们需要将式（4）从ECEF坐标系转换为站心（ENU）坐标系中[10-11]，转换矩阵为

式（4）在ENU坐标系中表示为

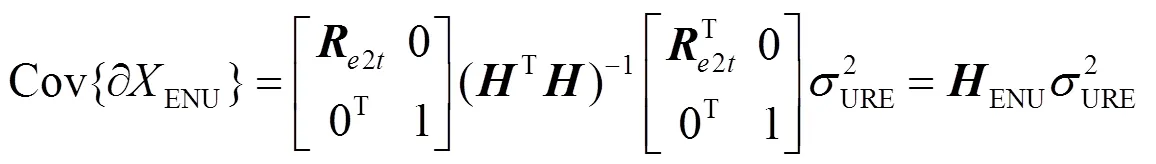
4种精度因子的计算公式再次证明了DOP只与可视卫星相对用户的几何分布有关，与卫星信号强度或接收机性能无关，高程约束定位方法对卫星星座布局的改善也必然会引起定位精度的提高。而推导高程约束定位方法的DOP计算公式，需要把地球椭圆方程对定位解算的影响等效到DOP计算公式中去。

2.2 高程约束定位方法DOP计算公式推导

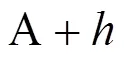
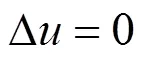
根据坐标变换矩阵式（7），式（10）等价于

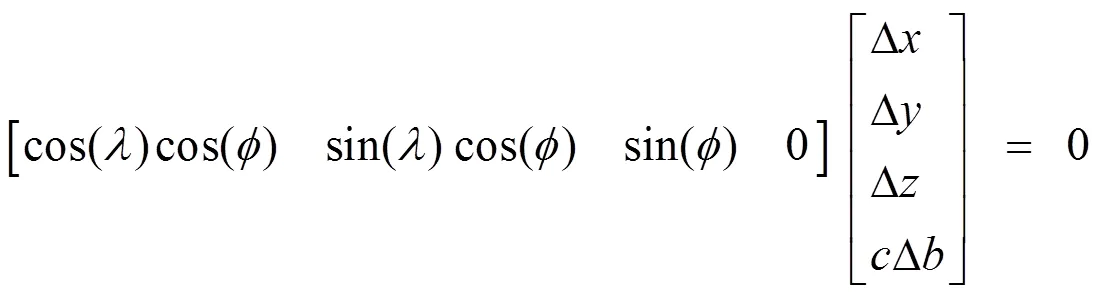
相应的式（2）变化为

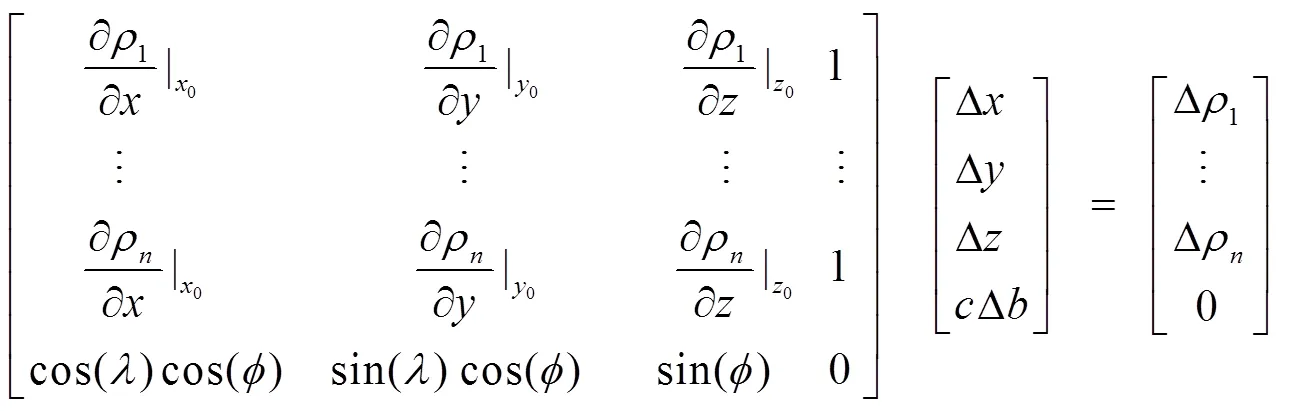
式（12）将地球椭球约束方程对定位解算过程的影响等效代入到观测方程中，4种常见DOP的计算公式不变。

3 实际数据的DOP分析

本文数据来自某一监测站的定轨数据，其中包含4颗GEO卫星和1颗IGSO卫星的24h实时星历数据，对应时间段为2015-09-21T 00: 00: 00/2015-09-21T23: 59: 59，用高精度接收机测定该监测站在ECEF坐标系中的坐标为：0＝-1 720 235，0＝4 997 184；0＝3 559 648，以该坐标作为ENU坐标系的原点。

为了验证上节推导出来的公式的合理性和高程约束定位方法的定位性能，根据采集的5颗卫星星历数据，以监测站坐标作为用户坐标，仿真了5颗卫星的伪距数据；对于定位试验，考虑到电离层延迟和对流层延迟等误差因素的影响，在伪距数据中加入了固定数值的误差项。本节将利用上述伪距数据验证高程约束定位DOP计算公式的合理性，分析该定位方法相对最小二乘方法的改善程度和高程估计精度对该方法的影响。本节的试验分为两种：DOP计算公式验证试验和定位试验。

3.1 DOP计算公式验证试验

本小节使用的数据是采集的5颗卫星星历数据和监测站坐标，计划进行两组试验：纯GEO星座的DOP分析试验和混合星座DOP分析试验。第1组试验只利用4颗GEO卫星的星历数据，第2组试验将加上IGSO卫星的星历数据。通过不同场景下的两组试验，比较两种定位方法的差异及DOP计算公式的合理性。

① 纯GEO星座的DOP分析

仅由GEO卫星组成的星座的DOP会很大，特别是其中的VDOP。图2显示了仅存在4颗GEO卫星时，最小二乘定位方法的PDOP值。

图2 4颗GEO卫星时最小二乘定位方法的DOP值

图2中PDOP和VDOP最大时能达到百万量级，此时根本无法定位。将图2放大后，可以发现大约80﹪时间的PDOP和VDOP是在600以下，PDOP最小时能达到67，此时定位结果可以收敛，但定位误差会比较大。

图3是高程约束定位方法的PDOP，VDOP变化情形，VDOP值在1附近变化，且变化范围特别小，在0.0002之内，与高程约束定位方法的原理相符合，即此时高程已经锁定。图中PODP值在6.9~13.5之间呈正弦变化，相对于图2有了极大地改善，说明高程约束定位方法可以改善DOP，而且相对于最小二乘方法效果非常突出。两幅图的变化情况完全符合第2节的理论分析，充分验证了高程约束定位方法DOP计算公式的正确性。

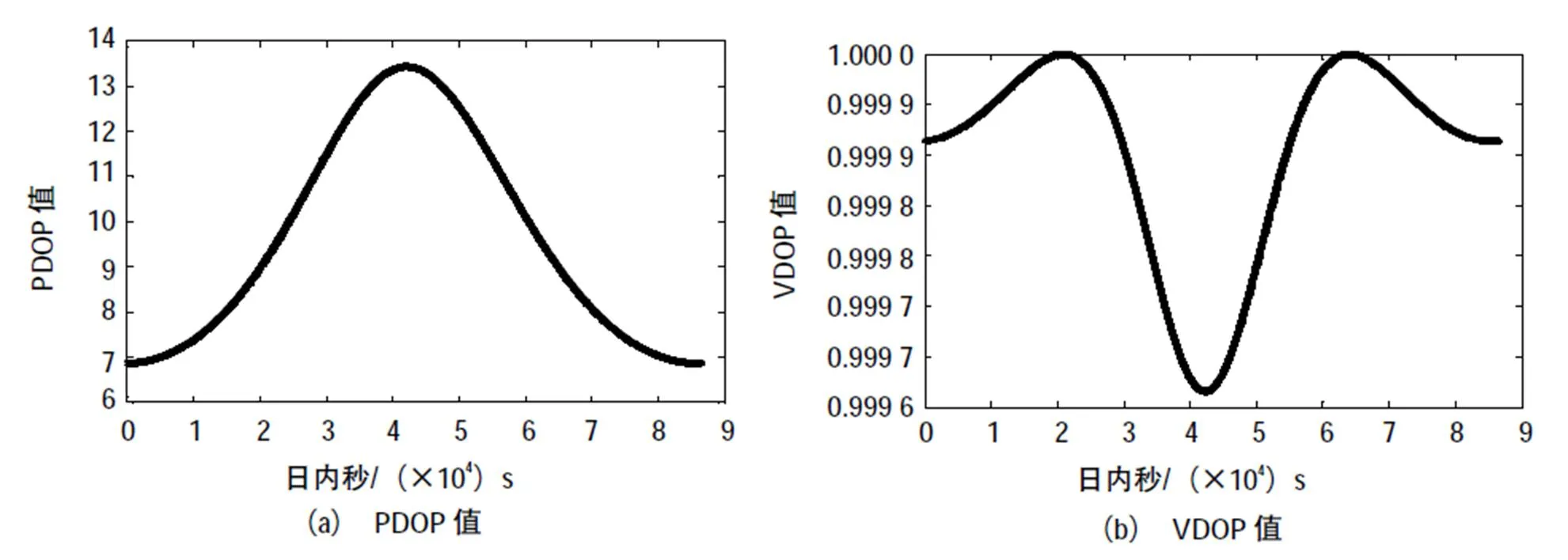
图3 高程约束定位方法的DOP值

② 混合星座DOP分析

IGSO卫星的引入可以极大地改善DOP，图4也验证了这一点，最小二乘定位方法的PDOP值在6~275之间变化，VDOP在5~175之间变化，都存在两个峰值，1d中大约80﹪以上的时间PDOP值在7以下，可以实现较高精度的定位。

IGSO卫星的存在使得图4中DOP值相对于图2改善很多，但部分时间DOP值仍然高达100以上，IGSO卫星的轨道特性使得它每天都会存在几段不可视时间，IGSO卫星不可视期间DOP值将会迅速恶化。高程约束定位方法可以解决这个问题，如图5所示，PDOP值最大只有10，最小可低至1.8，VDOP与图3一样，在1附近变化，变化范围极小。

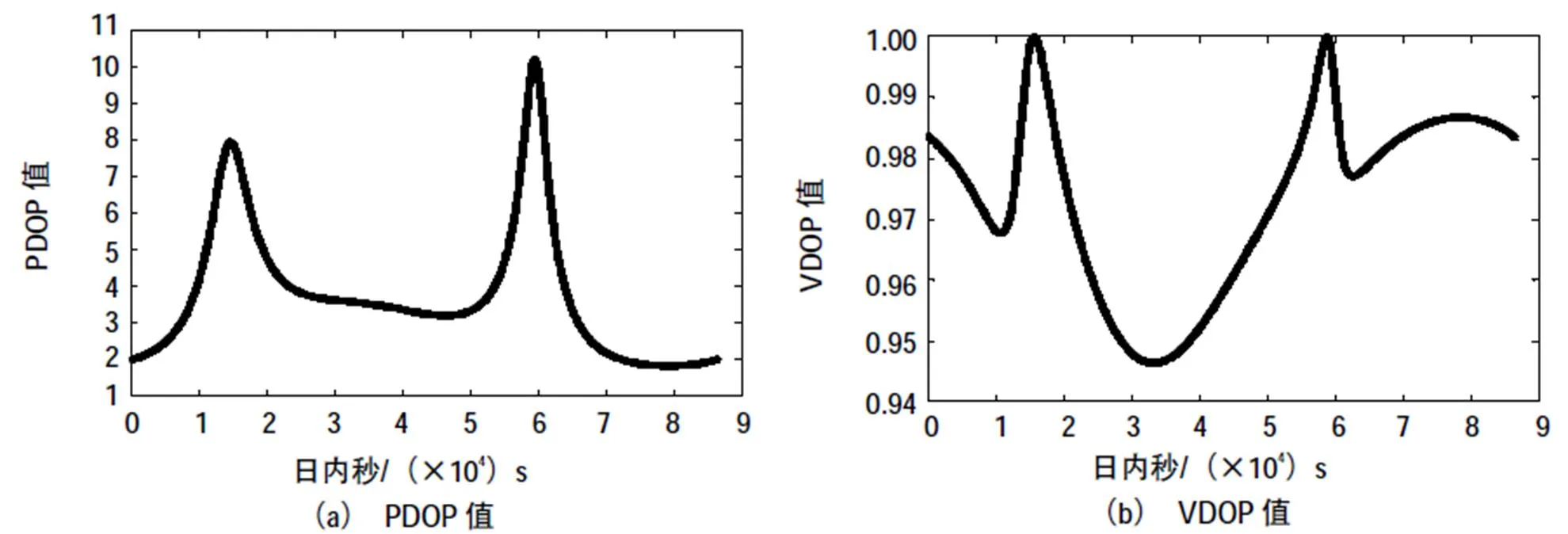
图5 GEO＋IGSO时高程约束定位方法的DOP值

本节的5颗星DOP分析试验和第2节的4颗星DOP分析试验的结果共同验证了高程约束定位方法DOP计算公式的合理性，多组试验的结果也与理论一致。

3.2 定位试验

3.1节是基于已知坐标的监测站，对两种定位方法的DOP值进行对比分析，本小节将从定位的角度去比较最小二乘方法和高程约束定位方法的性能差异。定位试验使用的伪距数据是利用卫星星历数据和监测站坐标仿真得到的，而且在4颗GEO卫星和一颗IGSO卫星对应的伪距上分别加了3，2，1，1和5 m的偏差。

定位试验分为两组，第1组是在地球椭圆约束方程中的高程是真值的条件下，比较两种定位方法的定位精度，以验证高程约束定位方法定位精度相对最小二乘方法的改进；第2组研究不同的高程估计精度下高程约束定位方法的定位精度，以验证高程估计精度对定位结果的影响，试验结果以表格的形式展现，为了排除伪距测量误差对试验的影响，第2组试验的伪距数据不加偏差。

① 两种定位方法定位精度比较试验

图6是最小二乘定位方法的解算结果。

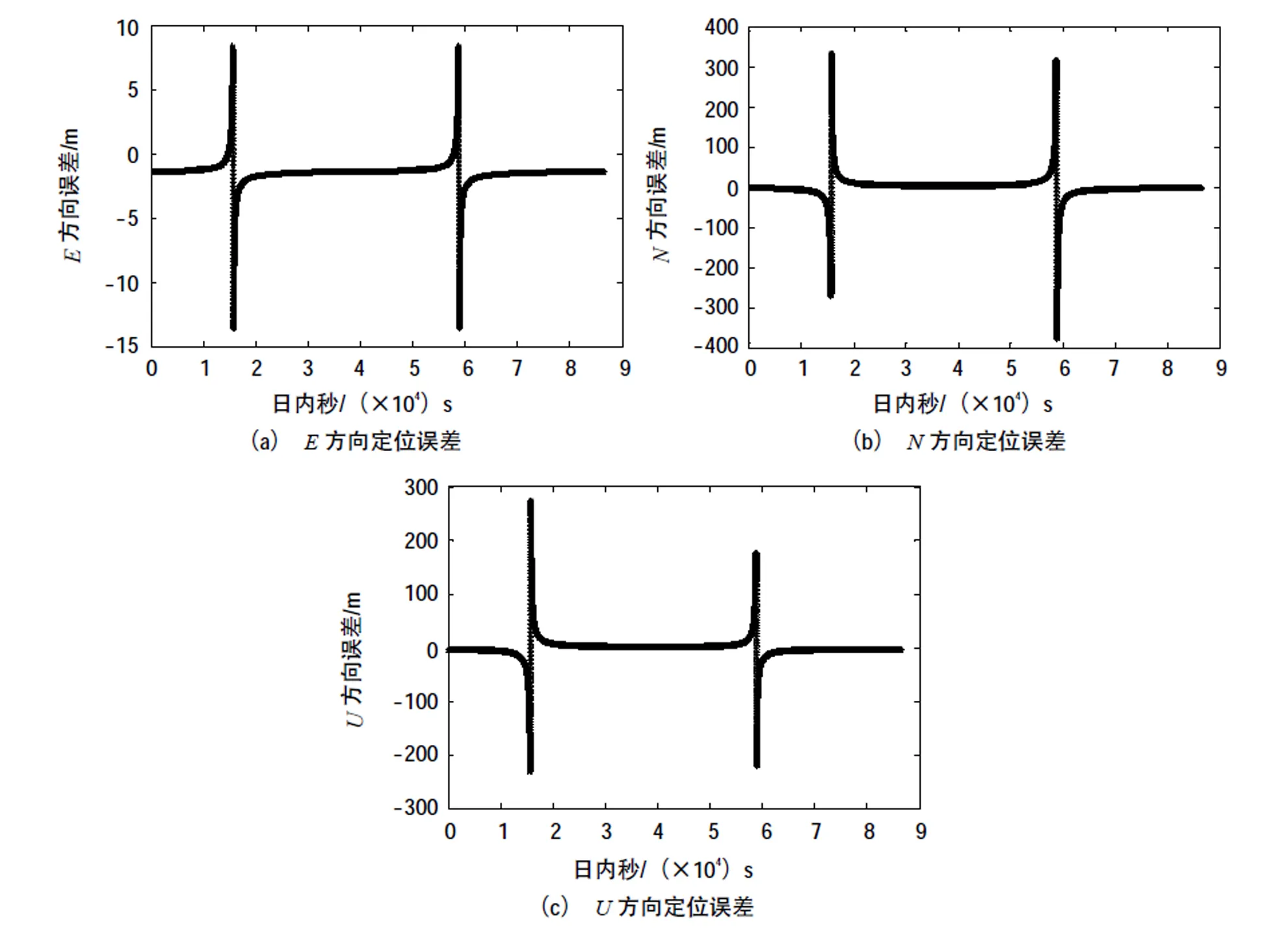
图6 GEO＋IGSO时最小二乘方法的定位结果

图6的3张图分别是，，3个方向上定位结果与真实值之差，其变化趋势与图4的PDOP值变化趋势一致，方向定位误差最小，都在10 m以下，甚至大部分时间都能小于2 m，，两个方向上定位误差能高达数百米。

图7中的定位结果相对于图5明显减小了许多，方向最大定位误差为2.2m，方向最大定位误差为15.9 m，高程一直被约束在真值附近，估计误差非常小，可以忽略不计，与高程约束定位方法算法原理一致。

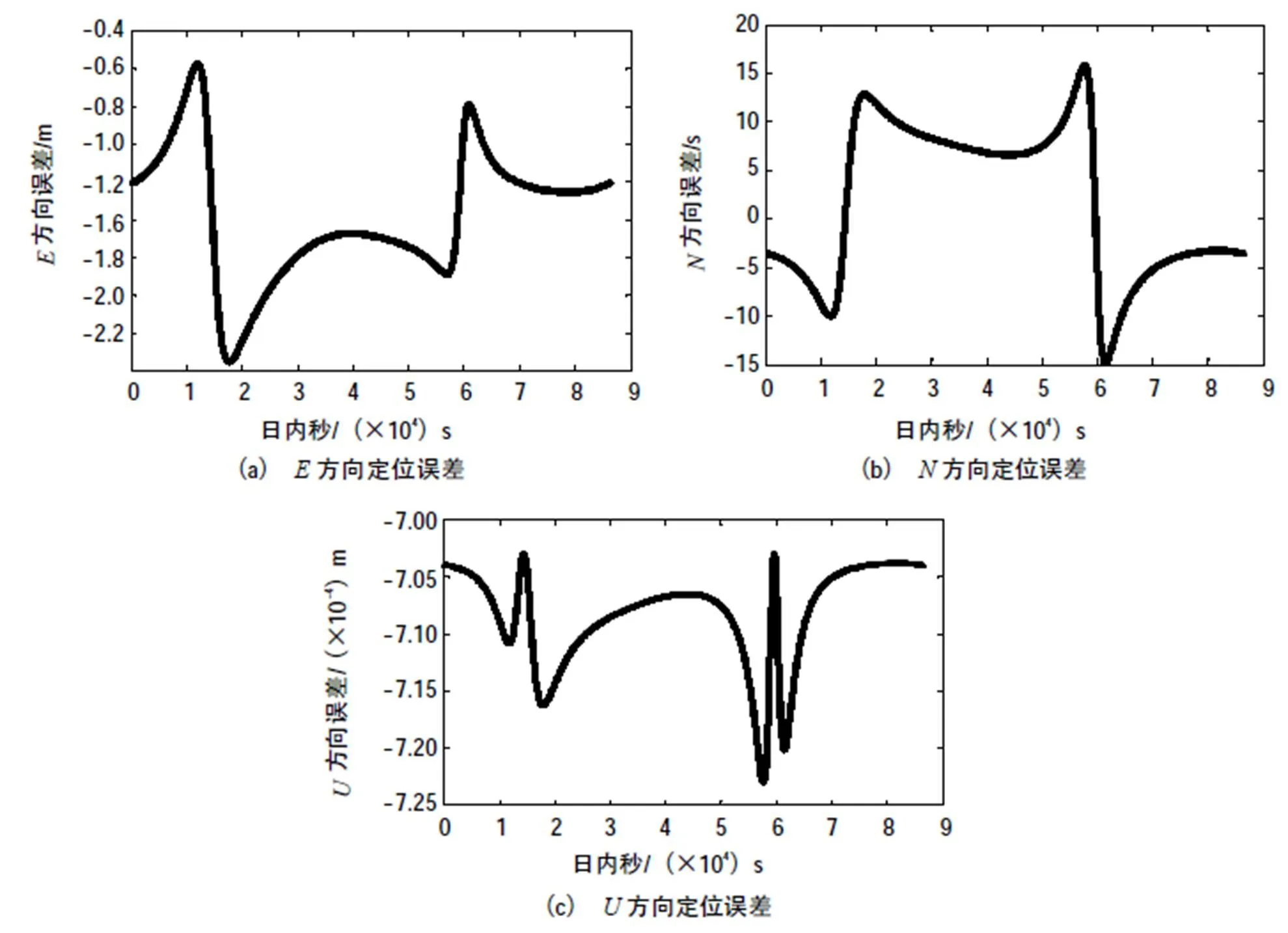
图7 GEO＋IGSO时高程约束定位方法的定位结果

定位结果的变化趋势与图5中DOP变化趋势一致，更是再次验证了高程约束定位方法DOP计算公式的正确性。

② 高程估计精度对定位结果影响试验

第1组试验没有考虑高程估计精度对高程约束定位方法定位精度的影响，但实际上，高程的精度对定位结果的影响不可忽视。

表1中高程估计精度是指地球椭圆约束方程中的高程值相对真值的偏差，第2~4列是不同高程估计精度时，3个方向上的定位精度，表格中的定位精度以1d定位结果的均方根误差表示。

表1 高程不同时定位误差统计 m

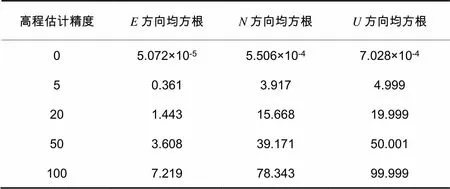
高程估计精度E方向均方根N方向均方根U方向均方根 05.072×10-55.506×10-47.028×10-4 50.3613.9174.999 201.44315.66819.999 503.60839.17150.001 1007.21978.34399.999

从试验结果可知看出，高程估计精度对定位结果的影响较大，特别是方向的定位结果受限于高程约束方程的解算方法，其定位误差与高程估计精度是一致的，，方向上的定位误差随着高程估计精度的降低而增加。但是如果对定位结果的要求不是很精确，有一定误差的高程也能满足实际的需要，如表1中第3行所示，当高程估计精度为20 m时，3个方向上的定位精度都在20 m以内，特别是方向上的定位精度可达1.443 m，能满足部分场合的实际需求。

4 结语

本文从DOP的计算公式出发，结合高程约束定位方法原理及解算方法，在不改变DOP物理意义的前提下，推导了高程约束定位方法的DOP计算公式，并利用来自某一监测站的GEO卫星和IGSO卫星的定轨数据，对高程约束定位方法DOP计算公式进行验证，比较了两种定位方法的定位精度，试验结果表明，该DOP计算公式是正确的，而且高程约束定位方法的定位精度远高于最小二乘方法，只是其定位精度受高程估计精度的影响较大。本文的结论不仅提供分析高程约束定位方法DOP值的方法，还对推导其他定位解算方法的DOP值计算公式有借鉴意义。

[1] 刘成, 杜晓辉, 王萌. 附有高程约束的中国区域定位系统定位精度分析[J]. 全球定位系统, 2011, 1(3): 18-22.

[2] 蔡成林, 李孝辉, 吴海涛. 混合星座的精度因子与定位性能分析[J]. 测绘科学, 2009, 34(2): 67-69.

[3] 谢钢. 全球导航卫星系统原理——GPS、格洛纳斯和伽利略系统[M]. 北京: 电子工业出版社, 2013.

[4] KAPLAN E D. Understanding GPS Principle Sand Applications[M]. London: Artech House, 1996.

[5] 施浒立, 孙希延, 李志刚. 转发式卫星导航原理[M]. 北京: 科学出版社, 2009.

[6] 艾国祥, 施浒立, 吴海涛, 等. 基于通信卫星的定位系统原理[J]. 中国科学G辑: 物理学 力学 天文学, 2008, 38(12): 1615-1633.

[7] 艾国祥, 盛裴轩, 杜金林, 等. 应用于CAPS的气压测高虚拟星座[J]. 中国科学G辑: 物理学 力学 天文学, 2008(12): 1702-1710.

[8] 施浒立, 裴军. 转发式卫星导航定位系统量测方程解[J]. 中国科学G辑: 物理学 力学 天文学, 2008, 38(12): 1687-1701 .

[9] 常青. 基于最小二乘递推估计的GPS定位算法[J]. 北京航空航天大学学报, 1998, 24(3): 263-266.

[10] 胡稳才, 张杏谷, 黄丽卿. 全球定位系统的几何精度因子[J]. 大连海事大学学报, 2001, 28(4): 42-45.

[11] 陈小平, 滕云龙, 康荣雷, 等. 几何精度因子改进算法研究[J]. 电子科技大学学报, 2008, 37(S1): 27-30.

Dilution of precision analytical method for satellite navigation system subject to height constraint

XU Jian1,2,3,4, WU Jian-feng1,2,3,5

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 2. Key Laboratory of Precise Positioning and Timing Technology, National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 3. Key Laboratory of Time and Frequency Primary Standards, National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; 4. University of Chinese Academy of Sciences, Beijing 100049, China; 5. Institute of Electronic and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101408, China)

The height-constrained positioning method is a way to improve positioning accuracy, which introduces earth ellipse constraint equation relative toleastsquaremethod. The introduced constraint equation changed the process of location solution, which leads to making computational formula of dilution of precision originated from leastsquaremethod not applicable to new method. Aiming at the issue, combining the definition of dilution of precision and the theory of the height-constrained positioning method, a new method to compute dilution of precision in the height-constrained positioning method is proposed. Two analytical tests of dilution of precision and an analytical test of positioning were done with the monitoring station data collected from the geostationary orbit and inclined geosynchronous orbit satellites. The test results show that the method is correct and the positioning accuracy of the height-constrained positioning method ishigher than that of the least square method.

height constraint; dilution of precision; least square

P228

A

1674-0637（2018）02-0120-10

10.13875/j.issn.1674-0637.2018-02-0120–10

2017-11-18；

2018-01-16

中国科学院“西部之光”人才培养计划资助项目（2013YB06）；高精度定位实验资助项目（Y519ZR1601）

徐健，男，硕士，主要从事卫星导航定位方法与技术研究。