多站联合星地时间同步及预报性能分析

杨伟锋，唐桂芬，苏冉冉，李晓杰



多站联合星地时间同步及预报性能分析

杨伟锋1,3，唐桂芬2，苏冉冉2，李晓杰2

（1. 北京市海淀信息中心，北京 100063；2. 北京卫星导航中心，北京 100094；3. 北京信息技术研究所，北京 100094）

无线电双向法通过上行与下行观测量比对实现星载钟与地面站时间同步，比对过程中消除或削弱了绝大多数的公共误差项，因此时间比对精度高。卫星不可视时该方法不能实施，此时卫星钟预报精度只能依赖卫星钟自身的物理性能，不可视弧长越长卫星钟预报精度衰减越快。为了削弱因卫星不可视带来的精度损失，多站联合星地时间同步是一种有效的解决方案。给出了多站联合星地时间同步的基本原理、推导了时间比对模型，并利用COMPASS实测数据分析了多站联合时间同步及预报性能，实验结果表明，多站联合观测有效延长了卫星的可视弧长，为提升卫星钟预报精度提供了数据基础。由于观测设备之间的系统性偏差，各站得到的星地钟差结果可能存在跳变，影响卫星钟预报精度。因此系统性偏差成为制约多站联合星地时间同步性能的关键性因素，系统性偏差的精确标定能确保多站联合星地时间同步及预报精度的大幅提升。

星地时间同步；卫星钟预报；系统性偏差

0 引言

卫星导航系统通过时间比对技术完成卫星钟与地面时间基准的钟差测定，并对钟差结果进行分析处理得到卫星钟的钟差预报参数，该参数与卫星轨道根数一起形成了导航用户使用的导航电文。卫星钟测定及预报精度直接影响了导航系统的服务性能，因此，高精度星地时间比对与预报技术是卫星导航领域的关键技术之一[1-5]。

无线电双向法能通过上、下行双向同步观测比对实现星地钟差测定，比对过程中能消除或削弱上、下行观测数据中的绝大多数公共误差项，因此，被认为是目前精度最高的星地时间同步方法。该方法受卫星可视性约束，在卫星不可视弧段内，星地时间比对不能实施，在此期间，卫星钟预报精度依赖星载钟自身的物理特性，一般来讲，不可视弧长越长，预报精度越低，并随时间推移衰减速度加快。

基于当前国产原子钟技术水平，利用无线电双向法能实现2 h 2 ns，10 h 10 ns的预报精度。也就是说，卫星超过10 h不可视时，由卫星钟预报带来的URE（user range error）误差超3 m以上。事实上，单站观测时卫星不可视弧长可能还要更长，预报精度还会进一步衰减[6-7]。为了弥补单站观测的弧长限制，多站联合星地时间比对技术成为一种有效的解决方案。通过多站联合观测，能有效延长星地时间比对弧长，缩短卫星不可视带来的卫星钟预报精度损失。以北斗卫星导航为例，仅在中国境内布站，能将IGSO（inclined geosynchronous orbit）卫星不可视弧长由单站的10 h缩短至6 h，MEO（medium earth orbit）卫星不可视弧长由单站20 h缩短至10 h。

本文研究了联合多个地面站观测数据进行星地时间同步的理论方法，并利用北斗实测数据进行了多站联合星地时间同步与预报的实验，结果表明：通过多站联合能够将卫星的可见弧长延长约35%，为高精度卫星钟预报提供数据基础，大幅提高了预报精度。

1 多站联合星地时间同步基本原理

多站联合星地时间同步的基本原理如图1所示：设有个地面站，以某一地面站作为基准站，其他地面站作为辅助站。根据卫星可视情况，以充分利用地面站资源、尽可能多地获取星地观测为基本原则，确定卫星的跟踪计划。卫星在基准站可视范围内，由基准站对卫星进行跟踪观测，基准站不可视时，由可视的辅助站进行跟踪观测，辅助站将观测数据通过站间数传链路发送到基准站统一进行时间比对处理，得到卫星相对各地面站的星地钟差。为了实现联合星地时间同步，还需要在卫星与辅助站的星地钟差中扣除辅助站与基准站之间站间钟差，这样就能把辅助站的观测结果归算到基准站。辅助站与基准站之间的站间钟差通过卫星双向时间传递精确测定。

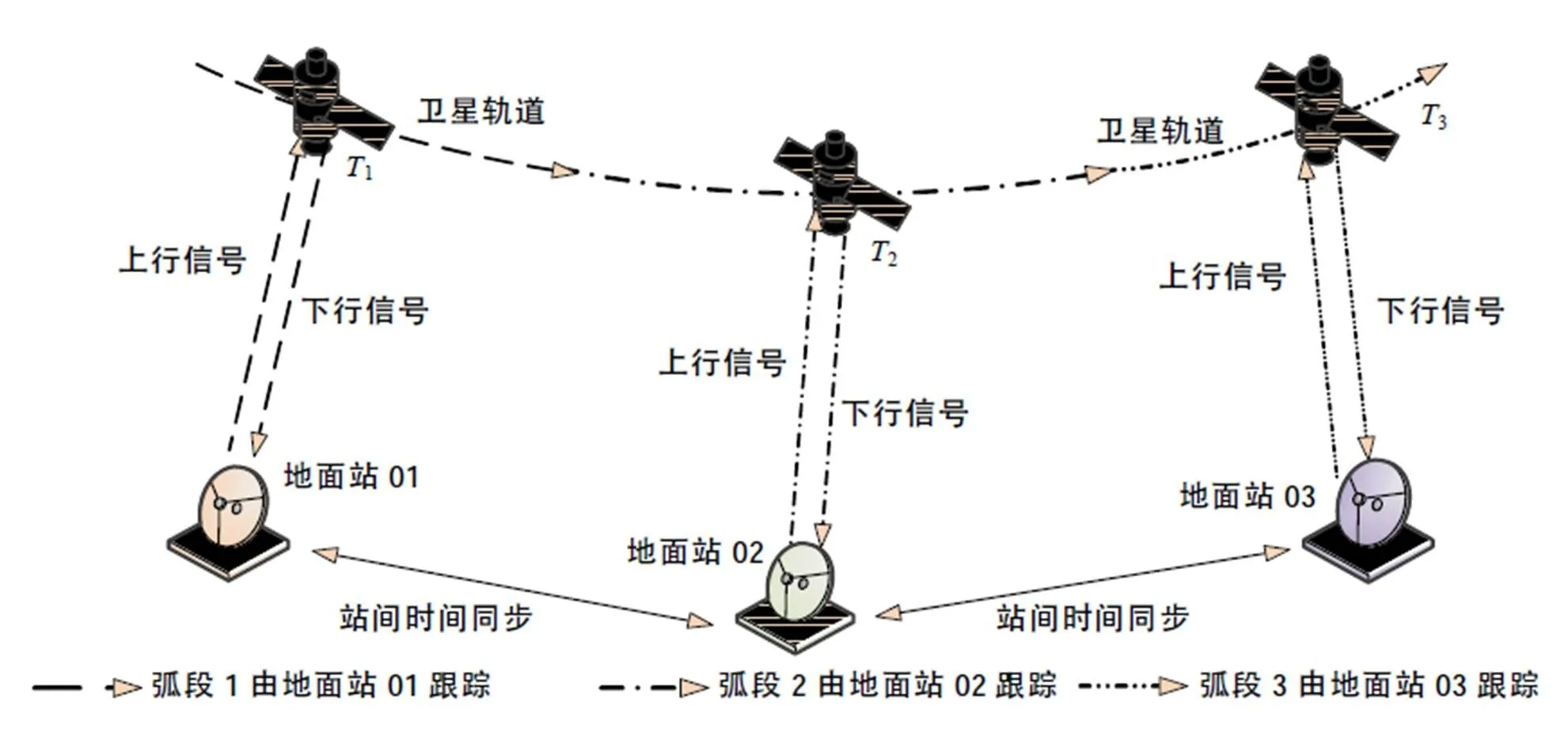
图1 多站联合星地时间同步原理图

1.1 无线电双向星地时间比对

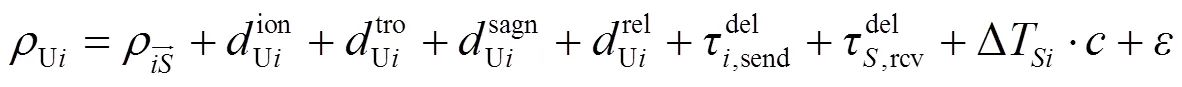
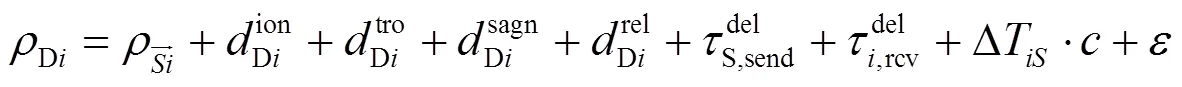
由式（1）和（2），可得到星地钟差比对结果为：

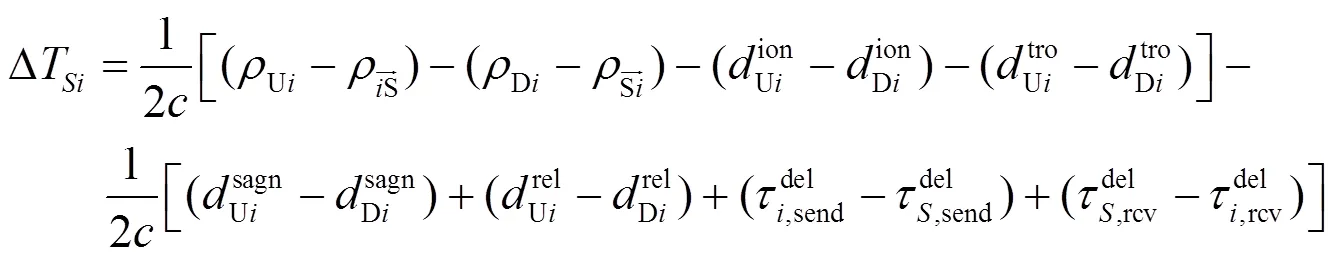
式（3）中各项含义与式（1）和（2）中相同。各地面站均采用相同的时间比对技术完成卫星与地面站的钟差比对。

1.2 辅助站星地钟差归算

为了联合使用多个地面站的星地钟差比对结果，必须把辅助站的星地钟差归算到基准站，这样得到的星地比对的结果才具有统一的时间基准。设地面站1为基准站，则有：

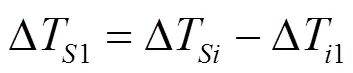
1.3 基于卫星双向传递的站间时间比对

卫星双向时间传递的基本原理是：两个需要时间同步的地面站经同一个GEO卫星转发器转发对方站测距信号，双方同时进行伪距测量，获得两个双向观测量，比对这两观测量得到站间钟差[8-9]。其具体过程是：地面站A，B分别在本地钟面时控制下发送测距信号，这两个信号经卫星接收并进行透明转发后分别被地面站B，A接收，以本地钟作为参考，两个地面站测得两个伪距时延。这两个伪距中包含大小相等方向相反的站间钟差，因此有：

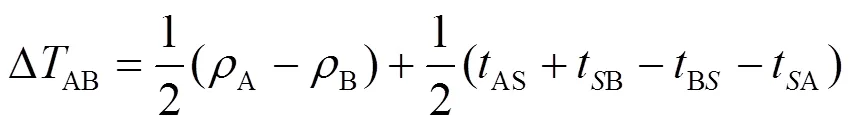
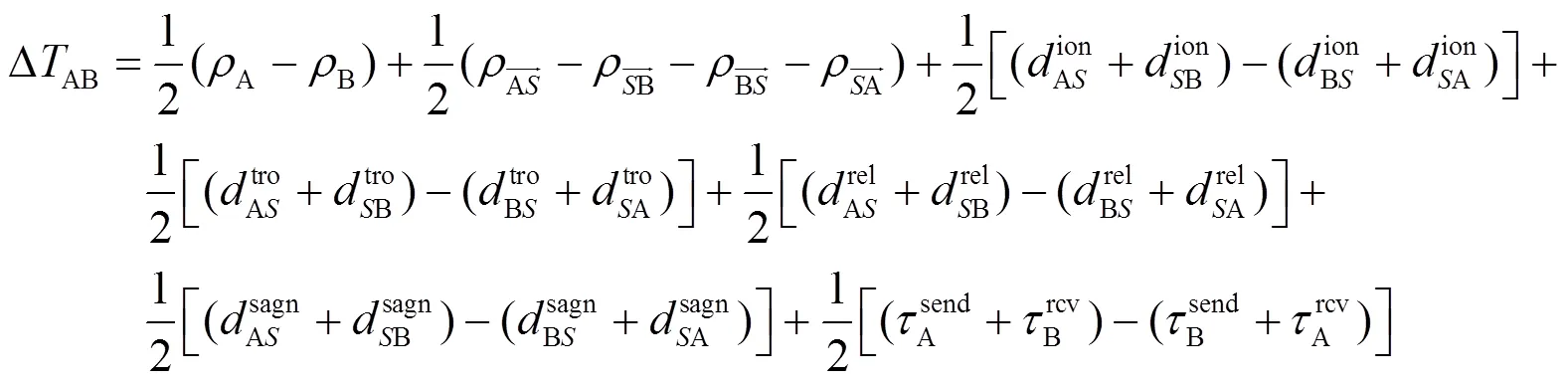
2 实验与结果分析

我们利用COMPASS系统2颗卫星的实测数据进行试验分析，其中卫星08为IGSO卫星，卫星14为MEO卫星。参与跟踪卫星的地面站为分布在中国境内的1、3和5号站。图2给出了两颗卫星2013年7月1日至7月2日的多站星地时间同步结果。

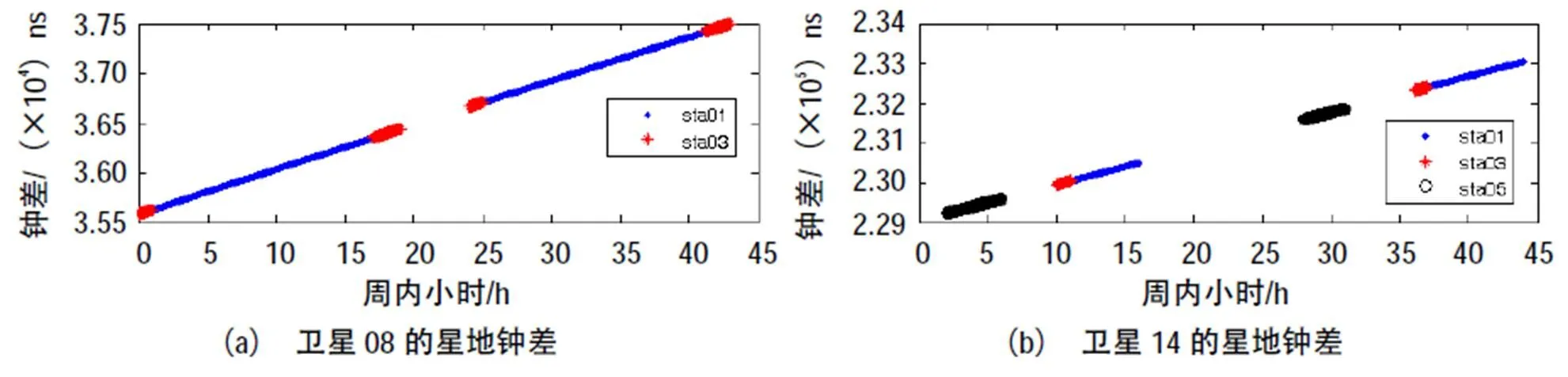
图2 多站联合跟踪卫星08和14的星地钟差结果

由此可见，多站联合跟踪有效延长了卫星可视弧长，仅中国境内布站就可将移动卫星的可视弧长延长30%。对导航用户来讲，卫星钟比对精度体现在卫星钟预报精度上，卫星钟预报精度是钟差预报值与实际比对值之间的差。钟差预报值的计算方法是：对比对钟差序列进行二次多项式拟合得到预报参数，再利用预报参数外推得到。图3和图4分别给出了单站和多站跟踪时的卫星钟预报误差结果，表1给出了相应统计信息。

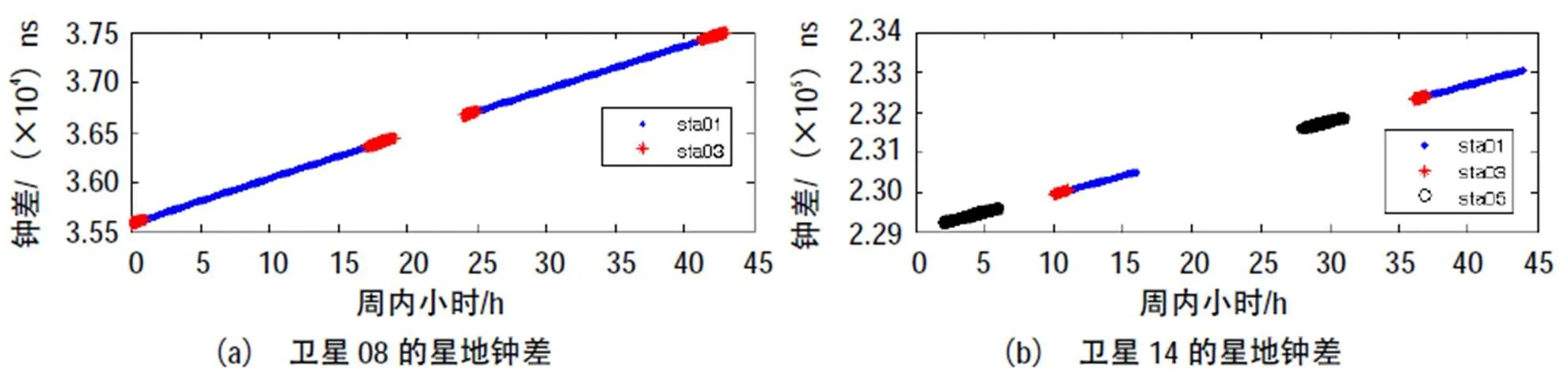
图3 单站跟踪卫星钟预报误差

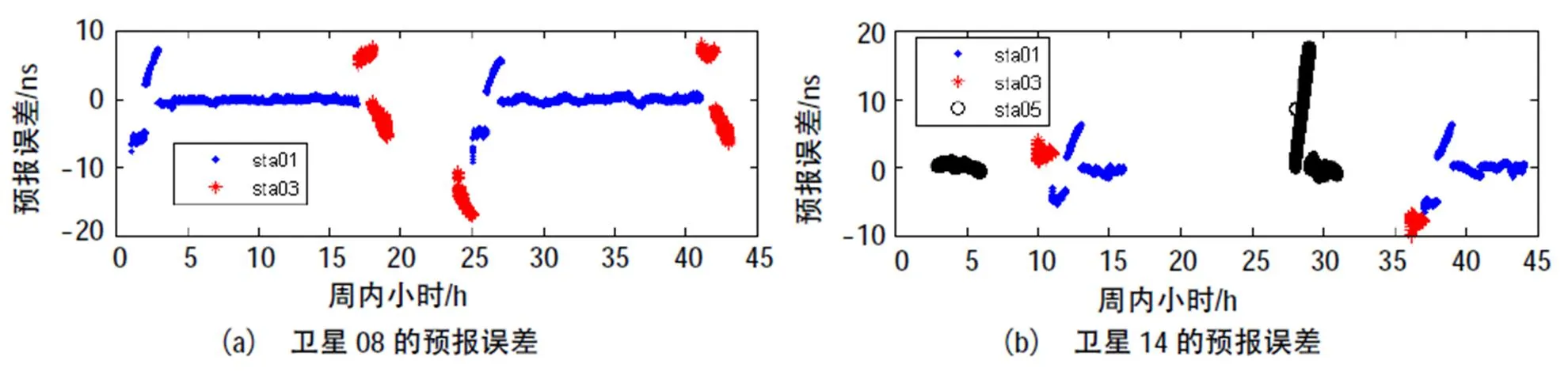
图4 多站跟踪卫星钟预报误差结果

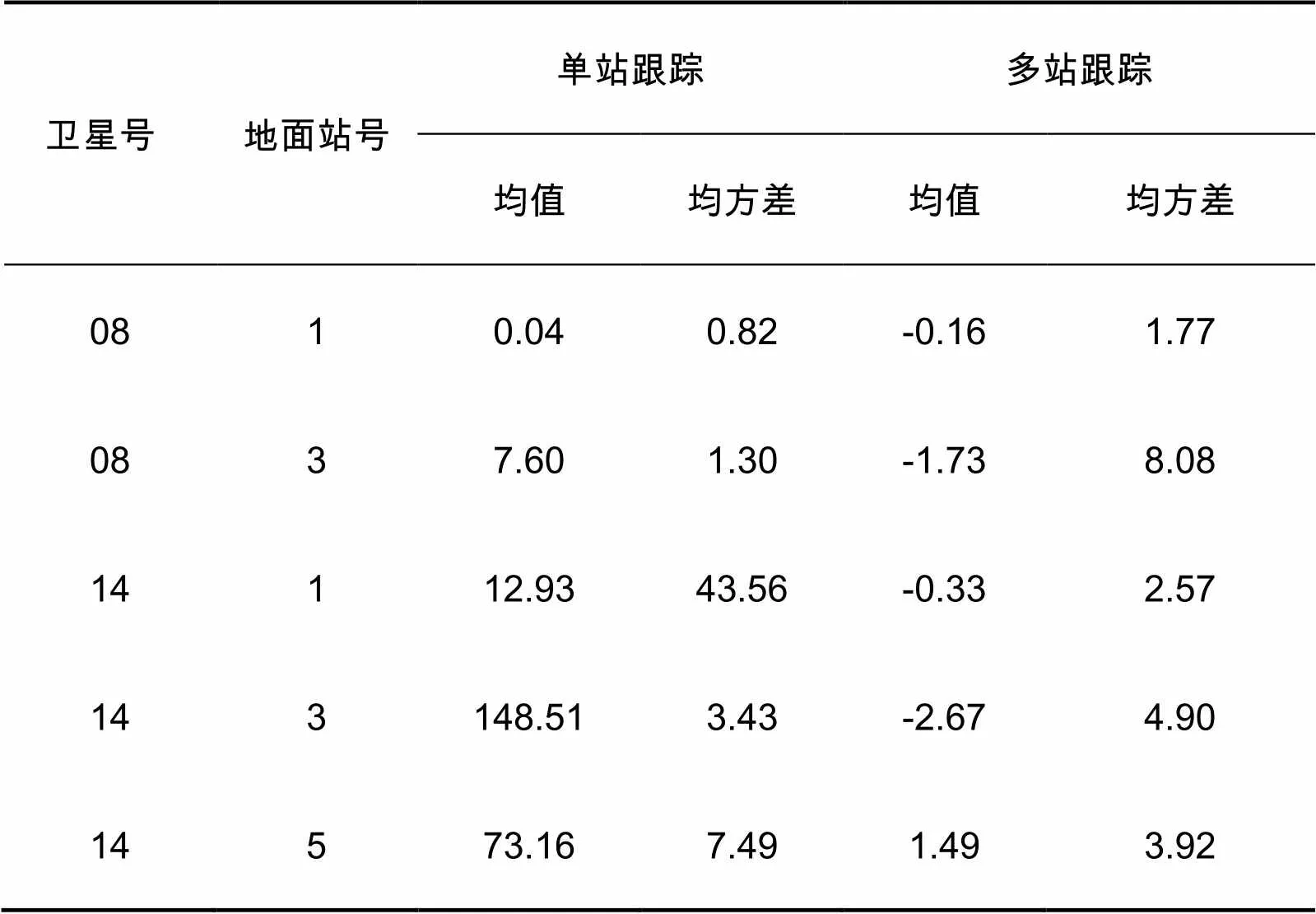
表1 单站与多站跟踪卫星钟预报误差统计结果 ns

单站跟踪时，用于预报的历史观测数据仅采用单个站的观测结果，其他站的观测结果用于检验预报精度；多站跟踪时，用于预报历史观测数据利用了所有跟踪站观测结果。从图3中可以看出仅单站跟踪的时候，卫星不可见时长较长，特别是MEO卫星，星载钟预报精度衰减较快。从图4可以看出，多站联合观测后，卫星钟预报精度大幅提升。

从图3和4中我们还发现跟踪站切换时候，预报误差明显发生跳变，表1的统计结果也显示3号站和5号站的预报误差结果明显要比1号站差。考虑到星载原子钟的二次线性物理特性，我们扣除星载原子钟的线性项，得到星地钟差二阶线性残差结果，进一步分析钟差比对结果性能，如图5所示，表2给出了拟合误差统计结果。

图5 卫星08和14的星地钟差二阶线性残差结果

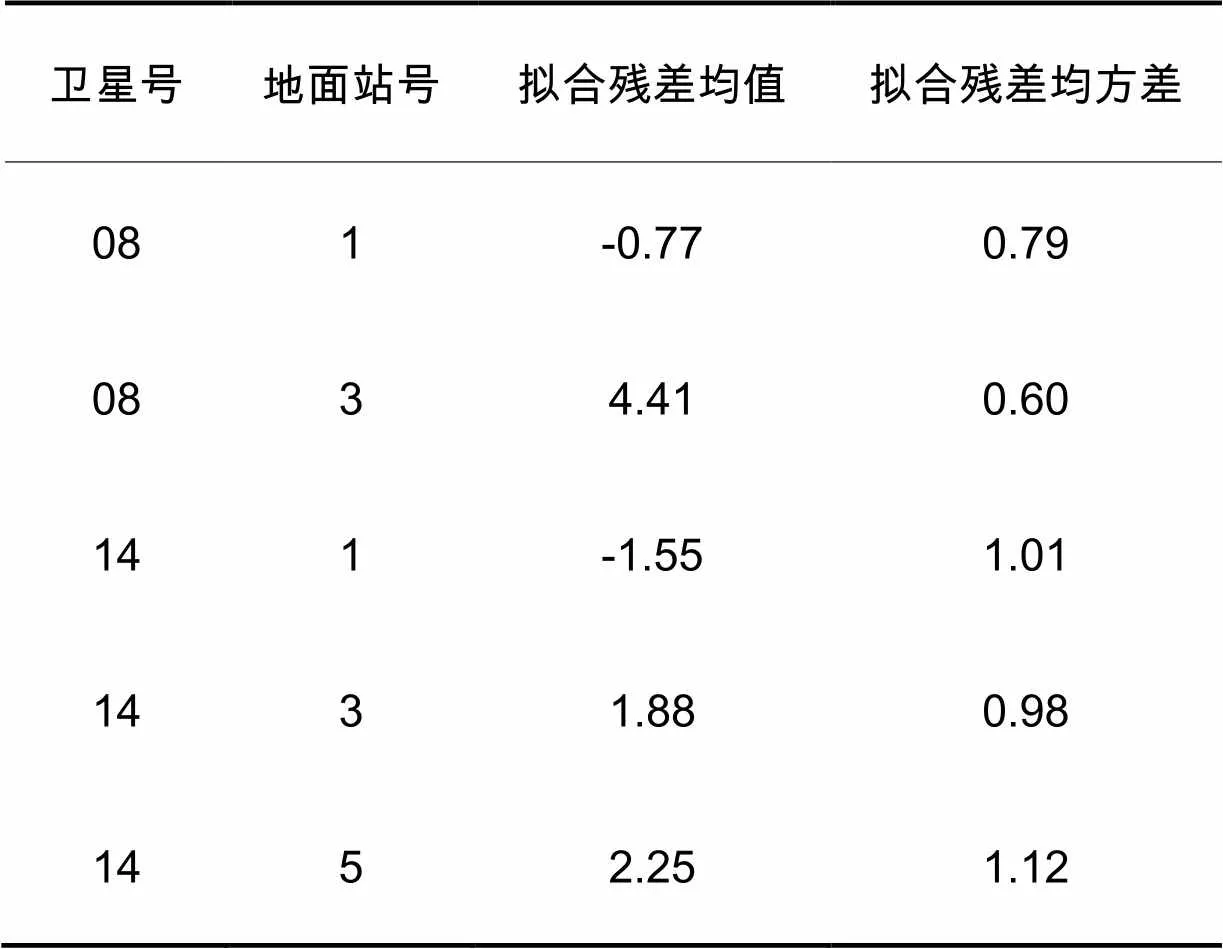
表2 卫星钟拟合残差 ns

由于各观测站采用了相同的时间比对模型，设备观测精度也一致，那么各跟踪站星地钟差结果的差异主要表现在：① 设备时延之间的系统性偏差；② 辅助站到主控站星地钟差之间的归算需要扣除的站间钟差，站间钟差误差会代入归算后的星地钟差。事实上，由于地面钟的稳定度远远高于星载原子钟，站间时间比对精度优于1 ns；而另一方面时间传递设备测量方法和精度很难统一。因此，观测设备之间的系统性偏差成为多站联合星地时间的关键因子。因此可以确定图5中钟差的跳变是由于观测设备的系统性偏差引起的。

下面进一步分析系统性偏差对多站联合星地时间同步的影响情况。下图是在实测数据中加上系统性偏差扰动进行的实验结果，分别加入了1 ns和2 ns的系统性偏差扰动2 h预报误差结果如图6所示，表3给出了更多系统性偏差扰动对预报误差的影响结果统计信息。

图6 系统差对卫星钟预报精度影响

表3 系统差对卫星钟预报的影响 ns

试验结果表明：系统性偏差在卫星钟预报，特别是短期预报中会被放大，也就是1 ns的系统性偏差会产生2.07 ns的预报误差跳变，2 ns的系统偏差差会产生3.32 ns的预报误差跳变，系统性偏差越大预报误差的跳变越大。这样带来的直接后果就是：由于系统性偏差的引入，多站联合星地时间同步预报精度不能得到保障。因此，尽管多个观测站联合是提升卫星钟预报精度的有效途径，但观测设备之间的系统性偏差是制约多站联合预报的关键所在。

我们按照文献[10]所提出的方法对各观测站系统性偏差进行解算，解算结果为3号站5.12 ns，5号站4.09 ns。利用该系统偏差解算结果对原始的观测钟差序列进行修订，修订后钟差序列二次残差如图7所示。

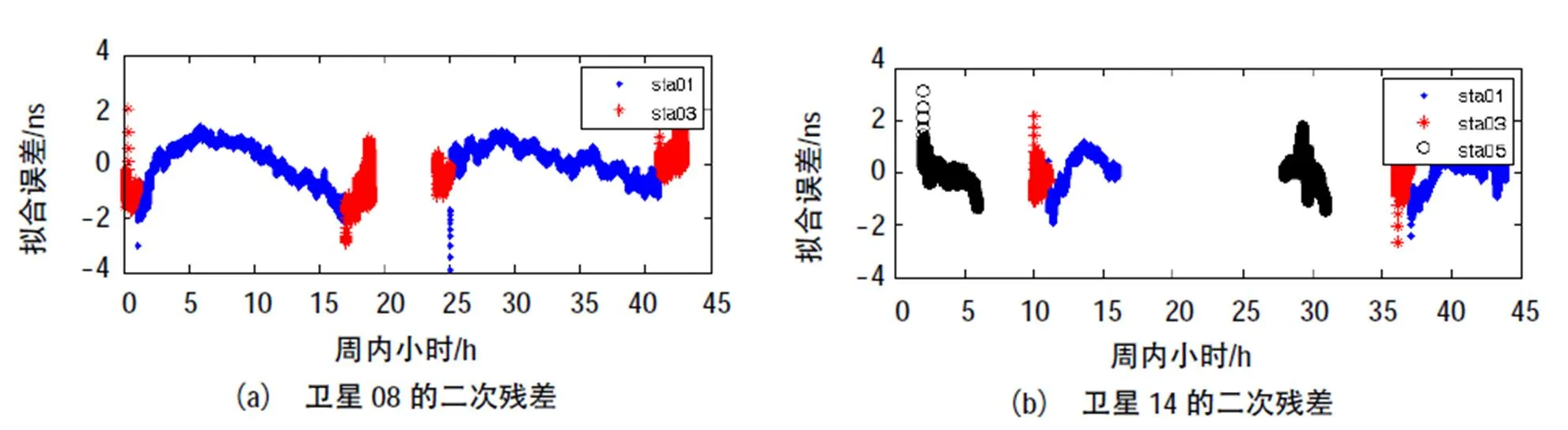
图7 系统差修订后卫星钟差序列二次残差结果

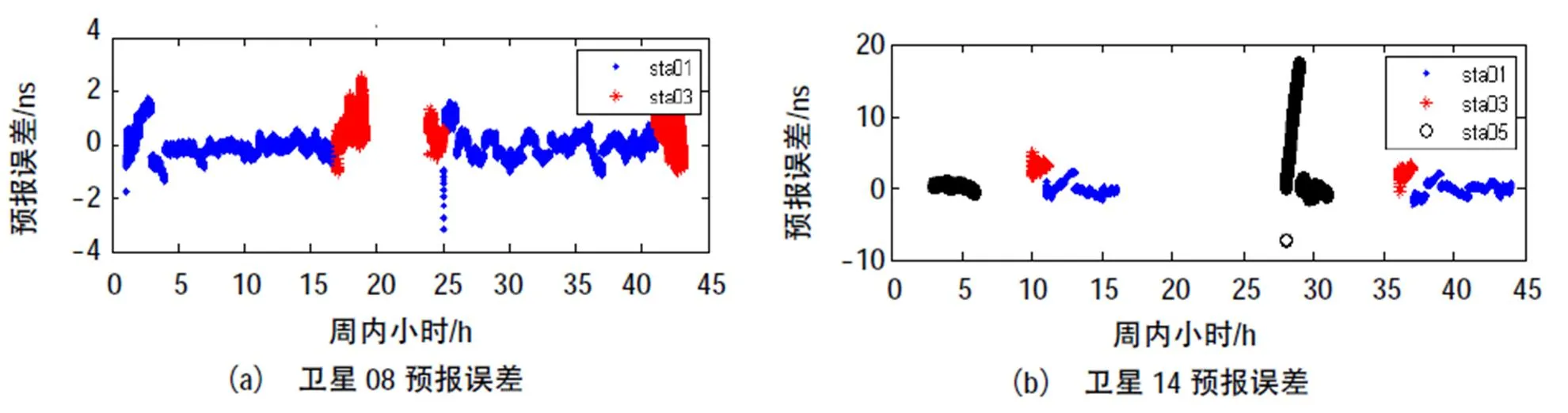
图8 系统差修订后的卫星钟差预报结果

表4 系统差修订后卫星钟拟合残差及多站跟踪的预报误差 ns

利用修订后的卫星钟差序列进行卫星钟预报，预报结果如图8所示，表5给出了系统偏差修订后钟差序列的拟合残差和多站跟踪的预报误差结果统计信息。

由上述结果可以看出系统差修订后，多站联合观测得到的钟差序列非常稳定，无钟差跳变现象，系统性偏差的精确标定能确保多站联合星地时间同步大幅提升卫星钟预报精度。

3 结论

论文给出了多站联合星地时间比对的基本原理，利用实测数据分析了多站联合的预报精度。理论分析与实验结果得出以下结论：

① 多站联合观测能有效延长卫星导航系统卫星可视弧长，仅中国境内布站就能提升约30%，是提升卫星全弧段预报精度的有效途径；

② 综合利用多站联合观测数据卫星钟预报精度能大幅提升；

③ 地面观测设备系统性偏差是多站联合星地时间同步关键。系统性偏差在卫星钟预报中影响放大，系统性偏差的精确标定能确保多站联合星地时间同步大幅提升卫星钟预报精度。

[1] 刘利, 韩春好. 卫星双向时间比对及其误差分析[J]. 天文学进展, 2002, 20(2): 219-226.

[2] 刘利, 韩春好, 唐波. 地球同步卫星双向共视时间比对及试验分析[J]. 计量学报, 2008, 29(2): 178-181.

[3] KIRCHNER D. Two-way time transfer via communication satellites[J]. Proceedings of the IEEE, 1991, 79(7): 983-990.

[4] 李瑞锋, 王元明. 星地双向时间同步技术在COMPASS中的应用[J]. 武汉大学学报: 信息科学版, 2013, 38(7): 842-846.

[5] 尹大伟, 陈忠贵, 朱俊, 等. 基于地面测量的卫星导航系统时间同步技术[J]. 飞行器测控学报, 2010, 29(1): 73-79.

[6] 唐桂芬, 许雪晴, 王群仰. 基于一种通用钟差模型的卫星钟预报方法[J]. 中国科学: 物理学 力学 天文学，2015, 45(7): 079502.

[7] 马卓希, 杨力, 贾小林. 基于多项式模型的改进卫星钟差预报方法[J]. 全球定位系统, 2016, 41(2): 27-33.

[8] TANG Gui-fen, LIU Li, SHI Xin. Performance analysis for time synchronization with compass satellite common-view[J]. The 3rd China Satellite Navigation Conference, 2012, 4(3): 483-487.

[9] 李瑞锋, 贺鹏, 乌萌. 基于双向C波段数据站间时间同步[J]. 测绘科学, 2012, 37(2): 20-23.

[10] 唐桂芬, 时鑫, 郭睿, 等. 时间同步系统差综合解算方法研究[C]//第二届中国卫星导航学术年会论文集, 上海: 第二届中国卫星导航学术年会组委会, 2011: 572-576.

Performance analysis of multi-station combined satellites and ground time synchronization and prediction

YANG Wei-feng1, TANG Gui-fen2, SU Ran-ran2, LI Xiao-jie2

(1. Haidian Information Center Beijing 100063, China;2. Beijing Satellite Navigation Center, Beijing 100094, China;3. Beijing Institute of information technology, Beijing 100094, China)

Two-way radio time synchronization can achieve high precise time comparison. The method doesn’t work when the satellite is invisible. In order to weaken loss of precision due to satellites are not visible, time synchronization combined multiple stations is a good choice. This paper presents satellite time synchronization method combined multiple stations, its basic principle and the time comparison model are deduced, and the performance is analyzed with real observation data from COMPASS system. The experimental results show: the method can prolong the visible arc length effectively, which provides a data foundation for improving the prediction precision of the satellite onboard clock. As there are systematic deviations between observing devices, clock offset sequence may occur jump, which will affect the satellite clock prediction precision. Therefore, the systematic deviation becomes the key factor to effect synchronous performance for multi-station combined time synchronization, and the accurate calibration of systematic deviation can ensure a substantial increase for time synchronization and onboard clock prediction precision for multi-station combined time synchronization.

time synchronization between satellite and ground; onboard clock prediction; systematic deviation

TN96

A

1674-0637(2018)02-0095-08

10.13875/j.issn.1674-0637.2018-02-0095–08

2017-11-21；

2017-12-28

国家自然科学基金资助项目（41174027）

杨伟锋，男，博士，主要从事星载原子钟数据处理技术研究。