基于Gamma随机过程的水工钢闸门时变可靠度方法

徐卫敏,卢鹏程,范兴朗

XU Weimin，LU Pengcheng，FAN Xinglang

(1.浙江建设职业技术学院,浙江 杭州 311231；2.浙江科技学院,浙江 杭州 310023；3.浙江工业大学建筑工程学院,浙江 杭州 310014)

结构在服役过程中,由于受荷载作用、材料内部作用和环境作用等因素影响,往往会引起其结构抗力和刚度的退化,从而带来正常服役可靠度的降低[1]。对于水工钢闸门结构而言,影响其抗力和刚度的最重要因素是钢板的锈蚀[2-3]。因此,为了预测现役钢闸门结构在未来使用期内的寿命,必须了解钢板的锈蚀规律,从而掌握其抗力和刚度随时间的变化规律。

引起钢板锈蚀的因素众多,主要有周围环境含有的腐蚀性物质(空气中的SO2含量等)、水中的酸碱性物质和腐蚀微生物等。另外,当钢闸门所处不同地理位置时,受当地风速、温度、泥沙以及水流流速等因素影响,其腐蚀程度也是不同的。文献[4]对收集国内水工钢闸门锈蚀检测的数据,确定了现役钢闸门锈蚀速率的概率分布模型。研究结果表明我国水工钢闸门锈蚀速率的均值和变异系数分别为0.034mm/a和0.43。文献[5]对部分工程实测数据的统计数据表明,锈蚀速率均值的变化范围为0.015～0.07mm/a,变异系数的变化范围为0.37～0.88。

在对已有钢闸门结构进行评估和维修规划时,考虑服役过程中承载力的退化规律是非常重要的。目前国内外学者已经对此进行了研究，Mlakar和Bryant[6]分析了平面钢闸门均匀腐蚀引起构件厚度减小时的可靠度。Patev等[7]在考虑腐蚀损伤对钢材屈服强度影响的基础上,分别采用了时变可靠性分析方法和危险函数方法分析了钢闸门的时变可靠度。周建方等[5]在总结闸门构件锈蚀规律的基础上对衰减函数为确定性函数和随机变量的情况钢闸门结构的时变可靠度进行了分析。研究结果表明,当衰减函数为确定性函数时,其计算结果偏于不安全。李典庆和常晓林的综述文章[7]对这方面的研究做了较为全面的总结。

从以上研究结果可以看出,尽管已有研究通过衰减函数考虑了钢板锈蚀对钢闸门承载力退化的影响,但是该函数并未考虑结构在演化过程中的时变随机性。实际上,钢板锈蚀的过程是一个随机累积的过程,相应的抗力衰减函数应该通过随机过程进行模拟。基于此,本文根据钢板锈蚀过程的基本特点,通过Gamma随机过程对锈蚀过程进行模拟,提出了一个基于退化的时变可靠度分析方法。

1　钢板锈蚀过程模拟及参数估计

实际工程中,影响水工钢闸门钢板锈蚀的因素众多,主要有锈蚀时间、锈蚀速度等,且这些因素大多具有不确定性。在数据较易获得的情况下,可以将各个因素处理为随机变量,并通过所得到的数据获得这些随机变量的分布类型和统计参数,然后采用Monte-Carlo的方法确定钢板锈蚀量的统计参数。对于大多数工程,获取这些数据难度较大,本文采用Gamma随机过程模拟钢板锈蚀深度。

Gamma随机过程是一种考虑独立、非负退化增量的随机过程,适合模拟具有微小增量的累积渐变过程,如疲劳、徐变和锈蚀等[9]。该过程可通过形状参数和尺度参数进行描述。

假定{d(t),t≥0}为一个随机Gamma过程,其概率密度函数可以表达为：

(1)

式(1)中:Gamma随机过程具有如下性质[10]：

1)d(0)=0；

2)对于任意的τ>t≥0,增量d(τ)-d(t)服从Gamma分布,即:

d(τ)-d(t)～Ga[α(τ)-α(t),λ].

(2)

3)d(t)是一个独立增量过程,即对于任意t12),各增量d(t2)-d(t1),…,d(tn)-d(tn-1)相互独立。

根据Gamma过程的性质,锈蚀量d(t)的平均值和方差可以表示为：

(3)

(4)

(5)

钢板锈蚀量可以通过改变Gamma过程形状参数α(t)来表征其随时间的变化规律。一般来说,α(t)可以表达成关于时间t的幂函数形式[1]：

α(t)=ctb.

(6)

对于特定的退化过程,通常可以根据相应的工程知识来确定相应的退化过程曲线形状参数。文献[11]列出了几种常见的退化过程参数b的值。本文取b为1.0。

对钢闸门结构进行可靠度评估时,当钢板锈蚀量数据足够时,形状函数α(t)中的参数c和Gamma过程的尺度参数λ可以采用最大似然估计法或者矩估计法进行确定[12]。但是对于大多数水工钢闸门而言,由于对结构某个区域连续监测或者历时较短的检测较难进行,本文主要通过已有锈蚀率的统计参数对进行参数c和λ进行反向标定得到。事先假定参数λ为某个固定值,根据式(3)并结合参数λ即可确定参数c。

确定参数后,锈蚀累积量可用下列顺序采样方法进行模拟[13]：

1)t=0,d0=0；将总时间T等分为n个子区间；

2)当t=ti时,产生服从Gamma分布函数Ga(α(ti)-α(ti-1),λ)的随机数Δdi,该随机数即为时段ti-ti-1内产生的锈蚀增量。ti时刻锈蚀累计量

di=di-1+Δdi;

3)重复过程2)直到达到总时间T为止。

2　时变可靠度计算方法

服役过程中由于各种环境因素会导致抗力退化,因此结构抗力R(t)是一个随时间递减的随机过程。目前国内外研究者通常将抗力R(t)表示为如下形式[14-15]：

R(t)=R0φ(t).

(7)

式(7)中：R0为初始时刻的抗力随机变量；φ(t)为抗力退化因子,当不考虑维修过程时,它是从1开始单调递减的。根据处理方式不同,φ(t)可以表示为确定函数和随机过程两种形式。

对于水工钢闸门结构,在初始厚度相同的情况下,φ(t)可以写成[5]：

(8)

式(8)中:D0表示钢板初始厚度。当构件各部分钢板厚度不同时,表达式相对较复杂。

结构的功能函数可以表示为:

Z=R(t)-S(t).

(9)

其中,R(t)和S(t)分别表示为结构的抗力与荷载效应,它们都是随机过程。根据可靠度的定义,在服役期间[0,T]内,结构失效的概率可以表示为

pf=1-Pr{R(t)>S(t)|∀t∈[0,T]}.

(10)

一般情况下,式(10)很难通过解析方式求解得到。因此,本文采用Monte-Carlo方法进行模拟求解。具体模拟过程如下：

1)给定钢板初始厚度d0、钢板锈蚀速率统计特征和服役时间T,确定Gamma过程统计参数；

2)根据抗力变量分布类型生成承载力初始值R0的一个样本值r0；

3)将服役时间T划为n个等子区间[t0,t1],[t1,t2],…，[tn-1,tn],根据Gamma过程分别计算t1，t2，…，tn时刻对应的锈蚀量d(ti),其中ti=iT/n,i=1,2,3,…,n；

4)根据荷载分布类型生成服役期T内n个荷载样本值si,i=1,2,3,…,n；

5)分别计算服役期内ti时刻对应的承载力r(ti)=r0φ(ti),其中ti=iT/n。如果对于i=1,2,3,…,n均有r(ti)≥si成立,则此次模拟结构安全；否则,结构失效；

重复步骤2)～5)直到满足模拟精度。若最终模拟次数为N,失效次数为M,则结构可靠度可近似采用nf=M/N表示。

3　数值算例及讨论

计算某水工钢闸门结构某构件在服役期T= 50 a内的结构可靠度。其承载力极限状态方程为：

Z=R-SW-SQ=0.

(11)

其中,R=φ(t)R0,R0为承载力初始值；SW和SQ分别为静水压力和其他活荷载对应的荷载效应。、SW和SQ的设计值存在如下关系：

R0K=1.5(SWK+SQK).

(12)

为后续计算方便,假定SWK=1.0,SQK/SWK=0.1,R0、SW和SQ的分布类型和统计参数分别见表1。

表1　随机变量统计参数和分布类型

计算中,事先假定参数λ为0.5,参数c通过锈蚀率计算得到。计算中考虑了三种不同锈蚀率(0.03mm/a、0.05mm/a和0.07mm/a),及三种不同的钢板初始厚度(20mm、25mm和30mm)和不同的衰减函数形式确定函数形式和Gamma随机过程。

图1表示三种不同锈蚀速率时钢闸门时变可靠度变化情况。从图1可以看出,当锈蚀速率为0.07mm/a时,经过50年服役期,可靠度从3.92降低为1.73。锈蚀速率越大,可靠度降低越多,且随着服役年限增大可靠度降低越多。

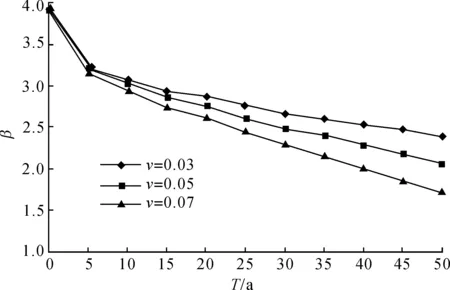
图1　不同锈蚀率条件时变可靠度变化情况

图2表示为三种不同初始板厚时钢闸门时变可靠度变化情况。从图2可以看出,当钢板初始厚度为25mm时,经过50年服役期,可靠度从3.92降低为2.06。当钢板初始厚度从20mm变化到30mm时,在T为50年时,可靠度变化0.45,变化幅度较锈蚀速率缓慢。

图2　不同初始厚度条件时变可靠度变化情况

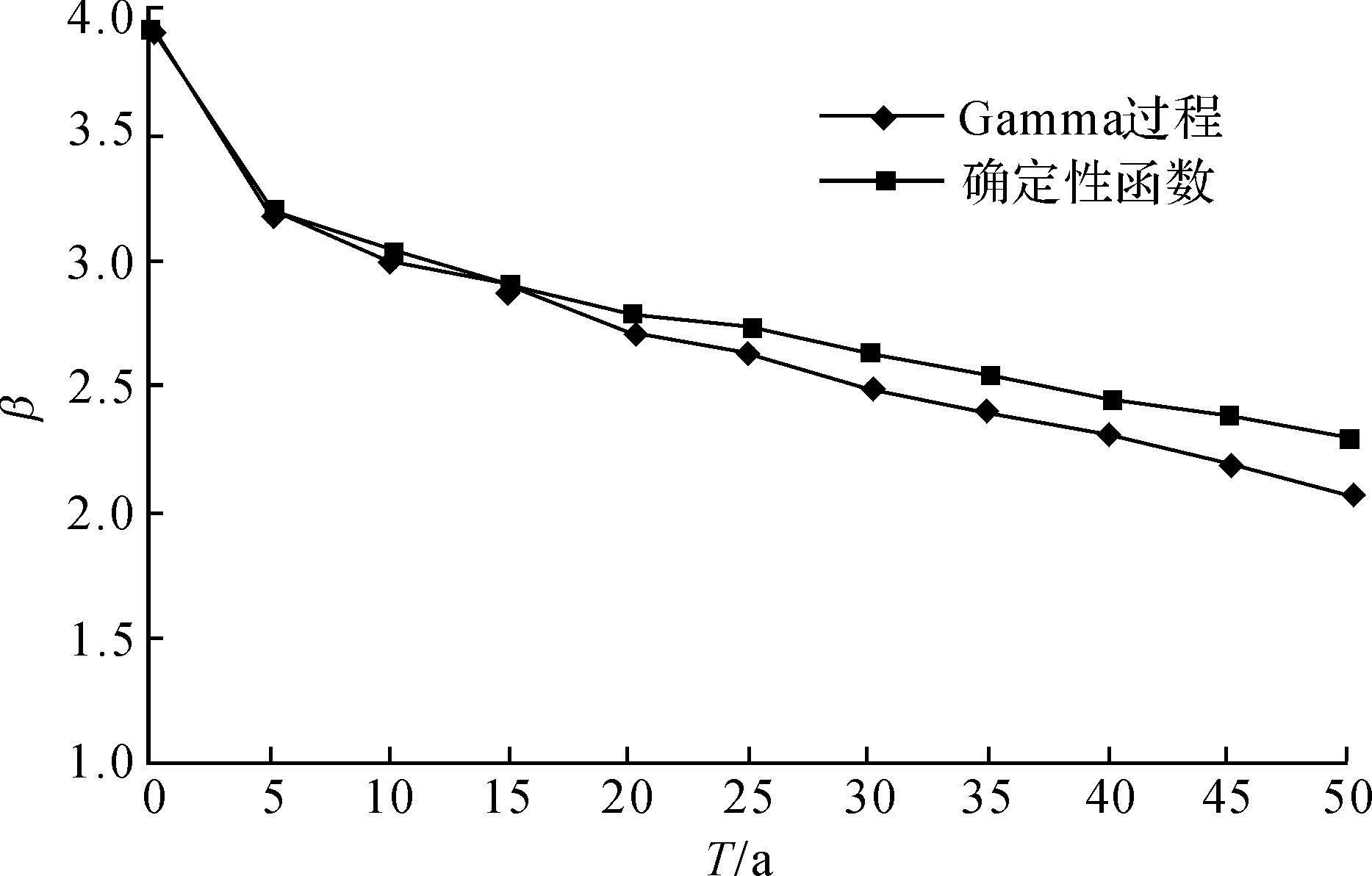
图3　不同衰减函数条件时变可靠度变化情况

图3比较了采用确定性衰减函数和Gamma退化过程时钢闸门时变可靠度的变化情况。从图3可以看出,在服役寿命早期,采用两种形式对可靠度计算结果影响不大；当服役寿命超过30年后,两者差别逐渐加大,且采用确定性衰减函数计算时计算结果偏于不安全,这是与文献[5]的结论相一致的。

4　结　语

鉴于目前正在运行的钢闸门有许多已经达到或超过了规范规定的折旧使用年限,故对在役钢闸门进行剩余寿命预测并进行加固维修势在必行。如何考虑由于钢板锈蚀引起钢闸门结构抗力退化进而导致结构可靠度降低是剩余寿命预测中的关键问题。本文根据钢闸门钢板锈蚀微小累积性和随机性的特点,采用Gamma随机过程对钢板锈蚀量进行了模拟,进而得到衰减函数的随机过程表达式,采用Monte-Carlo法对钢闸门结构时变可靠度进行了计算。研究结果表明：

1)相比于目前使用的衰减函数确定性函数和随机变量模型,本文将之扩展至随机过程模型。计算结果表明,采用确定性函数形式进行时变可靠度计算结果偏于不安全。

2)减小初始板厚度和增大锈蚀速率均可引起可靠度降低,且随着服役年限增大可靠度降低越多。相比于初始板厚度,锈蚀速率对时变可靠度的影响更大。