利用十字交叉法测试织物弯曲悬垂性
刘成霞, 周 澳
(1. 浙江理工大学 服装学院, 浙江 杭州 310018; 2. 服装数字化技术浙江省工程实验室, 浙江 杭州 310018)
织物弯曲性和悬垂性是影响织物风格和外观的重要属性,也是织物变形能力的直接体现[1-2]。前者最常用的测试方法为斜面法,除此之外,科技工作者们还研究了其他的方法,如提出了利用水滴法测试织物弯曲性[3],何琦辉等[4]提出了一种间接测试织物弯曲性的方法。关于织物悬垂性,目前的研究大都针对如何利用不同的图像处理技术进行悬垂指标的提取,如:李强[5]提出了一种利用仰视投影测量织物悬垂性的方法;黄新林[6]设计了一套新型图像法织物悬垂性测试系统;S. Farajikhah[7]提出了一种利用莫尔阴影地形图研究织物三维悬垂性的方法。
对现有方法和研究加以总结可发现,到目前为止,织物弯曲性[8-9]和悬垂性[10]的测试和研究都是分开进行的,即一种方法只适用于一种性能。但二者本质上有很大的共性:它们都对外观有重要影响,也都直接体现了织物柔软变形的能力,易弯曲的织物往往具有较好的悬垂性,悬垂性差的织物往往也不易弯曲。并且现有的弯曲性和悬垂性测试方法各自存在一定的问题,比如斜面法测弯曲性时,每次只能测试一块试样;圆台法不能测得织物某一具体方向的悬垂性,且最大问题在于这2种性能必须分开独立测试。
针对这些问题,本文尝试探索一种能同时测试这2种性能的方法,并且一次可以得到多块试样的弯曲性,也能表征织物某一具体方向的悬垂性,这样不仅可以简化操作,还能节约测试时间。
1 实验部分
1.1 试样的选取
选取变形能力差异较大的机织物共20种,规格参数如表1所示。

表1 织物规格参数Tab.1 Fabric specification parameters
注:C—棉;L—亚麻;S—蚕丝;W—羊毛; P—涤纶;V—粘胶。
1.2 斜面法测试织物弯曲性
根据GB/T 18318—2001《纺织品 织物弯曲长度的测定》,用YG(B)022D型全自动织物硬挺仪,在标准大气环境中测试表1中20块试样的经、纬向弯曲长度。
1.3 圆台法测试织物悬垂性
根据GB/T 23329—2009 《纺织品 织物悬垂性的测定》,用YG811型光电式织物悬垂性测试仪,在标准大气环境中测试表1中20块织物的悬垂系数。
1.4 十字交叉法测试织物弯曲和悬垂性
1.4.1测试装置及原理介绍
十字交叉法的测试原理是将2条长方形织物试条成十字形交叉放置于测试装置顶端,因此将该方法命名为“十字交叉法”,其测试装置如图1所示,由木条和三角尺构成,其中木条分为4组,每组形成一个端面,在每组木条的中间有一条凹槽,凹槽的中间嵌入三角尺,嵌入凹槽后的三角尺0刻度线刚好与木条表面平齐,三角尺可沿凹槽上下移动。在木条表面上标有厘米和毫米刻度。4组木条和4把三角尺用松紧带束扎固定。

图1 放置试样后的测试装置Fig.1 Instrument after putting fabric on it
测试时,将2条长条形试样垂直交叉放置于测试装置顶端,在织物顶端放一小重物,以防织物滑动。织物在重力作用下会自然下垂(见图1)。越柔软,悬垂性越好的织物,下垂幅度越大。纵向下垂距离N通过标在木条上的刻度读出;横向下垂距离M则可通过三角尺直接读出,如图2所示,这样就可快速读出4条试样的下垂距离。

图2 指标的提取Fig.2 Extraction of parameter
1.4.2试样准备
参照斜面法中试样的裁剪规格,将试样裁剪成为200 mm×25 mm的长方形,每种织物各准备 12个方向的试样,其中经向为0°,纬向为90°。即分别沿0°、15°、30°、……、165°裁剪织物,每个方向准备 2块试样。
1.4.3实验流程
1)在以上裁剪好的试样正中心打剪口做记号,将试样放置于测试装置的顶端,且使其剪口对准测试装置顶端面的中心,宽度方向与测试装置的木条表面平行。
2)按照上述方法,在第1条试样的表面垂直交叉地放置同一块织物的第2条试样,且2条试样中心处的剪口位置吻合,中心处再放一重物以防滑动(见图1)。
3)放置好试样1 min后,移动三角尺,使试样下垂一端的边缘与三角尺边缘相接触,读出接触点在三角尺上的读数,即为横向下垂距离M,然后读出三角尺在木条刻度尺上的读数,即为试样的纵向下垂距离N(见图2);由于同一块试样测试不同次数时,结果也会略有差异,所以在图2中,试条的两端下垂的横向距离M和纵向距离N并不一样,即图形并非对称。
4)定义弯曲悬垂系数ε=M/N,数值越小,则织物越容易弯曲,悬垂性也越好;
5)用同样的方法,读出其他3个方向的读数,共求出4个弯曲悬垂系数的平均值作为该织物的最后测试结果。
2 结果与讨论
2.1 不同方法所测弯曲性指标间的关系
如1.2所述,用斜面法测得20块试样的经、纬向弯曲长度,由于经纬向弯曲长度与十字交叉法所测结果非常类似,在此以斜面法所测的经向弯曲长度为例,将其与十字交叉法所测指标进行分析。斜面法所测得的弯曲长度与十字交叉法所测得的横向下垂距离M之间的关系如图3所示。
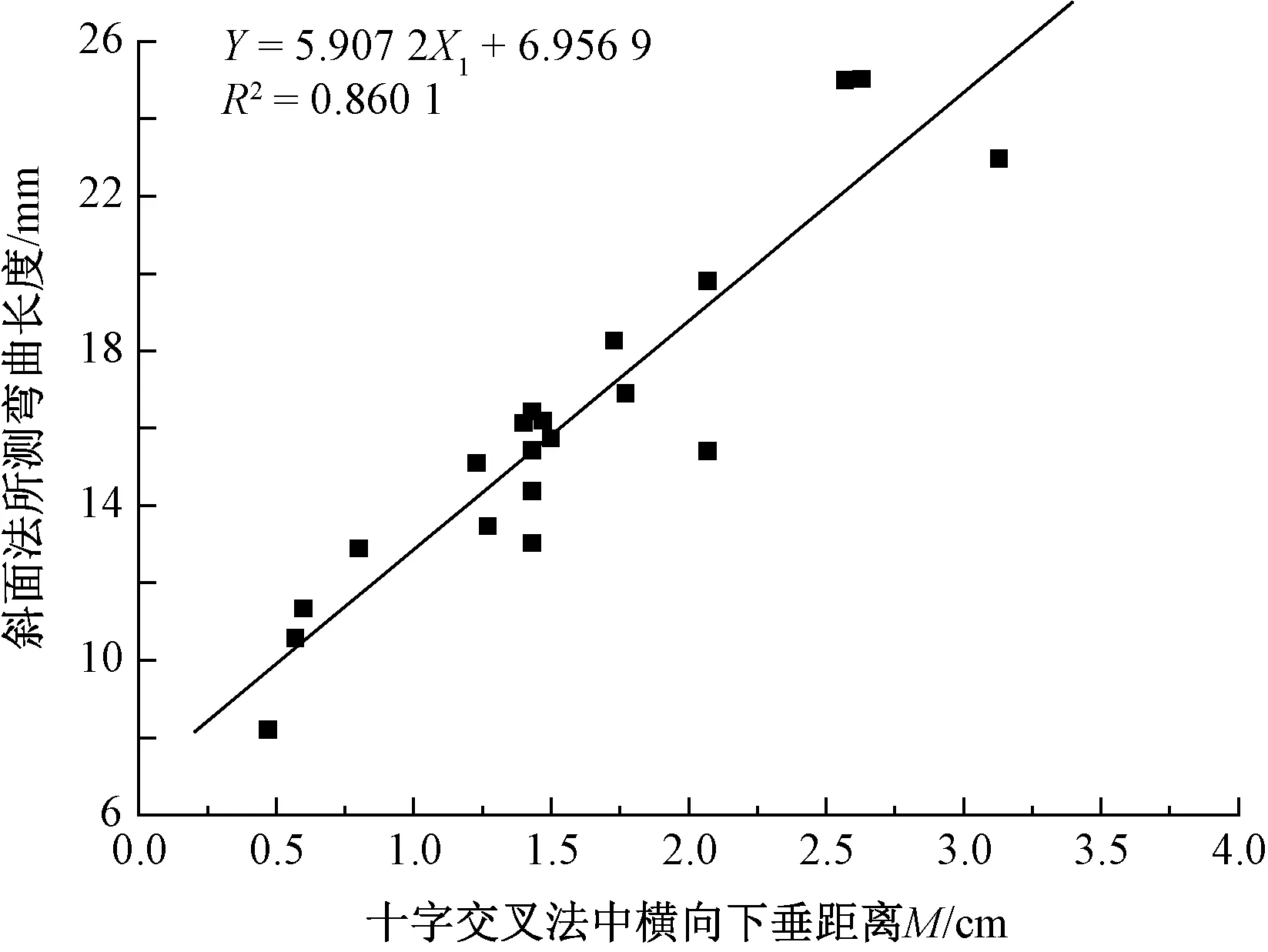
图3 横向下垂距离与弯曲长度之间的关系Fig.3 Relationship between horizontal drop width and bending length
从图3可看出,弯曲长度与横向下垂距离M呈正相关关系,即弯曲长度越大的织物,用十字交叉法进行测试时,织物试样下垂的横向距离越大。可以解释为弯曲长度越大,即越硬挺的织物,越不容易弯曲,用十字交叉法检测时,则图2中的M越接近于织物原来长度。即M为试样在水平方向的投影长度,N则是试样在垂直方向的投影长度。
图4示出用斜面法测的弯曲长度与用十字法测的纵向下垂距离N之间的相关关系。
由图可知,弯曲长度越小的织物,用十字交叉法进行测试时,织物试样下垂的纵向距离越大,呈负相关关系。可以解释为弯曲长度越小,即越柔软的织物,越容易弯曲,用十字交叉法检测时,纵向下垂距离N越大。即N越接近于试样本身的长度。
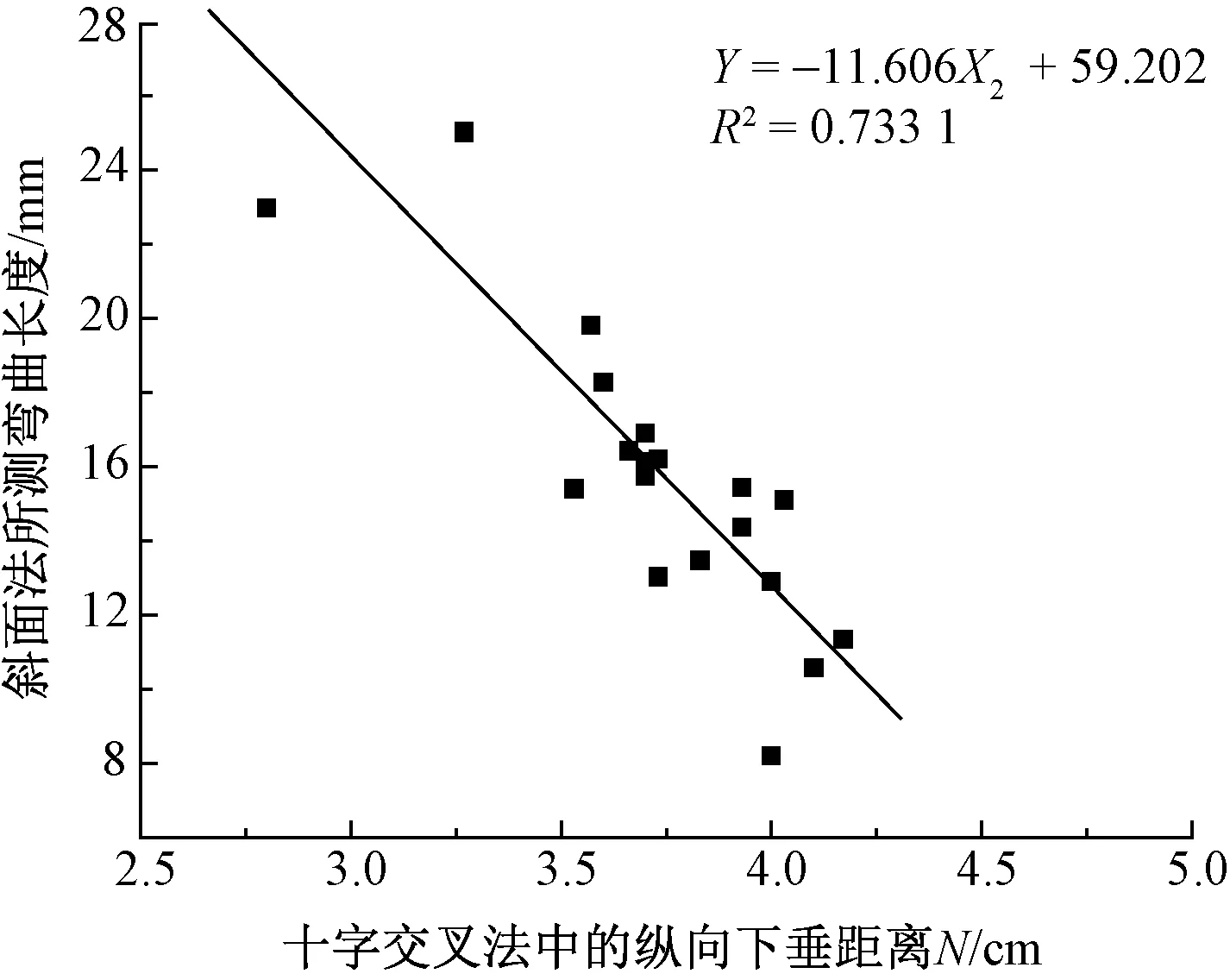
图4 纵向下垂距离与弯曲长度之间的关系Fig.4 Relationship between vertical drop width and bending length
对比图3和图4的相关系数R2可知,弯曲长度与横向下垂距离M的相关性大于纵向下垂距离N。
图5示出斜面法所测的弯曲长度与十字交叉法所测的弯曲悬垂系数ε之间的关系。二者具有良好的正线性相关关系,即弯曲长度越大的织物,十字交叉法所测的ε也越大,换句话说,越硬挺的织物,水平方向的投影M越大,纵向投影N越小。举个极端的例子,假定有一种无限硬挺、完全不会弯曲的面料,放到测试装置上之后,其纵向下垂距离为0,横向下垂距离则为织物本身的长度。从相关系数R2可知,弯曲长度与ε的相关系数大于横向下垂距离M和纵向下垂距离N。
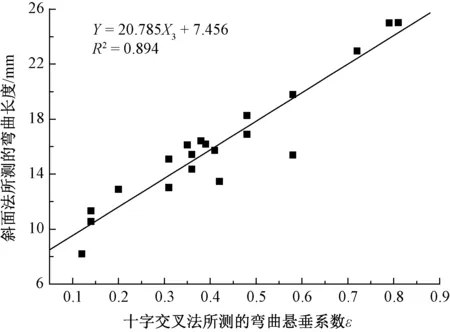
图5 弯曲悬垂系数ε与弯曲长度之间的关系Fig.5 Relationship between bending and draping coefficient ε and bending length
与斜面法相比,十字交叉法还具有以下优势:1)能同时测试2块试样,每块试样可以得到2个测试结果,而斜面法每次只能测试1块试样,只能得到1个测试结果,所以十字交叉法效率更高;2)由于用于读数的三角尺位于试样条的中间,所以相当于对织物的弯曲性指标求平均。在斜面法的测试中,一般只要试样条的一个点接触到斜面即开始读数,由于试样具有易变形性,这时试样另一端可能离斜面还有较大距离,也就是说传统的斜面法无法检测试样两个端点的中心点接触斜面时的弯曲长度,而十字交叉法则轻而易举地做到了这一点。
2.2 不同方法所测悬垂性指标间的关系
圆台法所测的悬垂系数与十字交叉法所测的弯曲悬垂系数ε之间的关系如图6所示。由于十字交叉法测试的试样为长方形,每次只能测一个方向的悬垂性,而圆台法所用试样为圆形,可以表征织物所有方向综合的悬垂效果,为使研究更具有科学性,图6中的弯曲悬垂系数ε为1.4.2中所测的织物 12个方向ε的平均值。
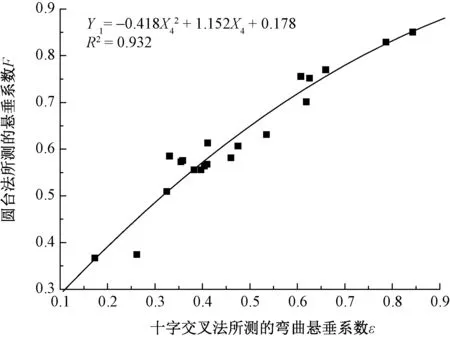
图6 弯曲悬垂系数ε与悬垂系数F之间的关系Fig.6 Relationship between bending and draping coefficient ε and draping factor F
由图6可知:弯曲悬垂系数ε与悬垂系数F呈正相关关系,其中X4为12个方向所测弯曲悬垂系数ε的平均值,Y为悬垂系数F。即F越大的织物,用十字交叉法进行测试时,ε也越大。也就是说,2种方法都可以测试织物的悬垂性,且测试原理具有相似之处,都是利用不同的织物在自身重力的作用下,下垂形成的形态不同导致投影不同。所不同的是,圆台法只能表征织物所有方向综合的悬垂性,而十字交叉法则能体现织物任何一个方向的悬垂性。前者比较适合裙子和桌布的等的悬垂性描述,而对于上衣、裤子、窗帘等具有方向性的织物来说,更适合十字交叉法。
3 结 论
本文以20块试样为研究对象,分别用斜面法测试其弯曲性能,用圆台法测试其悬垂性能,最后用自行设计的十字交叉法提取弯曲悬垂性指标,经过研究得出以下结论:
1)十字交叉法中的3个指标与斜面法的弯曲长度都具有较好的相关性,其相关系数由大到小依次为弯曲悬垂系数、横向下垂距离、纵向下垂距离。斜面法所测的弯曲长度与十字交叉法所测的弯曲悬垂系数之间的关系式是:Y=20.785X3+ 7.456,R2=0.894(X3为弯曲悬垂系数;Y为弯曲长度)。
2)十字交叉法所测的弯曲悬垂系数与圆台法所测的悬垂系数具有良好的正相关性,二者的具体关系式为:Y1=-0.418X42+1.152X4+0.3067,R2=0.932(X4为12个方向所测弯曲悬垂系数的平均值;Y1为圆台法所测的悬垂系数F)。
3)本文提出的十字交叉法既可用来检测织物的弯曲性,也可检测织物的悬垂性,将传统的织物弯曲性和悬垂性必须分开进行的测试合二为一,既简化了操作步骤,又节约了时间。
4)十字交叉法具有传统方法没有的优势,可同时得到多个测试数据、能检测织物试样条中心点的弯曲性,能表征织物任一具体方向的悬垂性。
致谢本文得到了“浙江省服装个性化定制2011协同创新中心”的资助,特此感谢。
参考文献:
[1] 杨萍.纱线与织物的弯曲刚度研究[D].上海:东华大学, 2002:12-20.
YANF Ping. Research on bending behavior of yarn and fabric [D]. Shanghai: Donghua University,2002:12-20.
[2] LIN H, STYLIOS G K. Prediction of post-buckling deformation in fabric drape[J].Journal of the Textile Institute, 2009, 100(1):35-43.
[3] 刘成霞,韩永华,张才前.基于图像处理的织物弯曲性能测试方法[J].纺织学报, 2013,34(7):52-56.
LIU Chengxia,HAN Yonghua,ZHANG Caiqian. Test for fabric bending behavior based on image processing bending behavior of fabric[J]. Journal of Textile Research, 2013,34(7):52-56.
[4] 何琦辉,王正伟,利用织物实际弯曲形态测试其弯曲性质的算法[J].纺织学报,2006,27(12):52-58.
HE Qihui, WANG Zhengwei. Arithmetic of bending property of the fabric based on its actual bending shape[J]. Journal of Textile Research, 2006,27(12):52-58.
[5] 李强,过玉清,纪峰.基于仰视投影的织物悬垂性测试方法[J].纺织学报,2008,29(3):34-37,46.
LI Qiang, GUO Yuqing, JI Feng. Testing method of fabric drape based on upward projection[J]. Journal of Textile Research,2008,29(3):34-37, 46.
[6] 黄新林.织物悬垂性测试方法及其装置的研究[D]. 上海:东华大学,2011:15-30.
HUANG Xinlin. Study of the test method and instrument of fabric drape [D]. Shanghai:Donghua University, 2011:15-30.
[7] FARAJIKHAHA S, MADANIPOUR K, SAHARKHIZ S, et al. Shadow Moiré aided 3-D reconstruction of fabric drape[J]. Fibers and Polymers, 2012, 13(7): 928-935.
[8] 倪红,潘永惠. 基于BP神经网络的织物斜向弯曲性能的预测[J].纺织学报,2009,30(2):48-51.
NI Hong, PAN Yonghui. Prediction of fabric diagonal bending rigidity by BP neural network[J]. Journal of Textile Research, 2009,30(2):48-51.
[9] 刘成霞,罗秋霞,施美琴.织物多方向硬挺度测试方法研究[J].现代纺织技术, 2015, 23(2):56-59.
LIU Chengxia, LUO Qiuxia, SHI Meiqin. Study on the measurement of multi-directional fabric stiffness[J]. Advanced Textile Technology, 2015, 23(2):56-59.
[10] 徐军,姚穆.织物悬垂性客观评价的研究[J].纺织学报,1999,20(4):11-14.
XU Jun, YAO Mu. A study on objective evaluation for fabric drape[J]. Journal of Textile Research,1999,20(4):11-14.

