偏振多光谱机器视觉的高反光无纹理目标三维重构方法

郝婧蕾，赵永强，赵海盟，Peter BREZANY，孙嘉玉

1. 西北工业大学自动化学院，陕西 西安710071； 2. 西北工业大学深圳研究院，广东 深圳 518057； 3. 北京大学空间地球与空间科学学院，北京 100871； 4. 维也纳大学，奥地利 维也纳 1090

三维重建技术能够获得目标表面的三维形貌[1-3]，在航天工程的空间任务中有着重要应用[4-5]。而空间碎片等空间目标具有表面光滑、纹理单一、易产生耀光的特点，给传统基于光学原理的目标三维重建技术带来了极大的挑战[6]。对于传统的基于视觉成像的目标三维重建方法，纹理稀疏甚至缺失会造成难以提取到足够的特征点，使得恢复结果只能得到边缘轮廓等部分信息；大面积的耀光会造成图像传感器饱和，丢失耀光处的数据信息，造成恢复结果会出现大面积的数据空洞。与传统方法相比，基于偏振视觉的三维重建技术无须利用目标表面纹理特征，同时偏振成像能够有效地抑制耀光。而在许多实际应用中，如非合作目标的相对导航﹑陌生环境中物体探测等，目标表面材料特性通常是没有先验信息的，因此本文提出了基于多光谱偏振的高反光无纹理目标三维重构方法，同时获得目标的折射率和三维形貌。

自然光(无偏光)经物体表面反射之后的反射光为无偏光与偏振光的叠加，通过对反射光偏振度的分析可以获取反射面法向量的天顶角，通过求取反射光的偏振相角可以求得法向量的方位角[7]。由此可见，反射光的偏振态与法向量有着密切关系，其偏振态包含了目标表面的形状信息[8]。文献[9]最先将偏振信息引入到目标三维重建中，通过分析绝缘体表面反射的圆偏振光偏振态的变化来求取目标表面的方向。该方法的缺陷在于入射光必须为圆偏振光。文献[10]利用圆偏振光作为光源分离了镜面反射与漫反射，同时完成了对目标材料折射系数的估计。文献[11]通过旋转待测目标获取不同角度的偏振图像解决了偏振度与法向量天顶角的二义性问题，实现了透明物体的三维重建。文献[12]提出了从不同视角获取偏振图像来解决单视角存在的凹凸二义性的问题，进而完成目标的三维重建，该方法无须进行不同视角下的图像匹配，提高了应用的灵活性。文献[13]通过结合近红外波段与可见光波段的偏振信息解决了偏振度与法向量天顶角的对应问

题，实现了目标三维信息的恢复。金属的折射系数不同于绝缘体材料，文献[14]推导出了金属目标的三维重建模型，进行了金属目标三维信息的恢复。文献[15]加入了一个多光谱采集系统，利用目标在不同波段下有不同偏振度的特性，解决天顶角模糊问题。文献[16]通过联合光谱和偏振信息，实现了基于卷积神经网络的多波段偏振相机的大视场重构。文献[17]从多视角偏振信息入手，重构黑色镜面目标的三维信息。文献[18]利用透明物体反射耀光的偏振信息来重构其内外表面的三维结构。

单纯依靠偏振成像进行目标的三维重建存在法线方向的二义性，得到的深度信息是像素坐标系下的相对深度。利用偏振成像获得的目标表面的几何信息再结合其他手段来解决方向二义性或者转化为绝对深度成为近几年计算机视觉的热点方向。文献[19]最先将偏振三维重建方法同光度立体法进行结合来恢复目标三维形状，该方法中光源方向与目标材料的折射系数为已知量。文献[20]改进了Atkinson的算法，将物体表面看作朗伯表面，通过光度立体法估计目标表面的法线方向，进一步估计出目标材料的折射系数。文献[21]将偏振三维重构扩展到高光谱图像，成功恢复了目标表面的三维形状同时获得了目标材料的折射系数。 文献[22]利用偏振得到的法向量信息为辅助，通过结合Kinect的粗略深度图得到了高精度的目标三维重建结果。文献[23]通过调整光源的方向获取偏振信息，将偏振信息与阴影信息作为目标表面法向量方向的约束条件恢复了目标表面的三维形状。文献[24]提出了基于偏振双目视觉的三维重构方法，解决了传统方法不能处理高反光、纹理单一的目标的问题。

本文提出一种新的方法来解决这个问题，通过分析从单一视角拍摄图像的光谱和偏振信息来实现目标的精确三维重构。相比已有的基于偏振信息进行三维重构的文献，本文的工作重点是使用反射光与偏振片旋转角度的正弦关系和菲涅尔理论，实现目标天顶角和折射率的同时估计。

1 基于偏振成像的目标三维重建

1.1 偏振成像原理

自然光属于非偏振光，但当自然光经物体表面反射后，反射光会变为部分偏振光。反射偏振成像过程如图1所示。基于偏振视觉进行三维重建的关键在于通过偏振成像获取反射光的偏振状态，并将其与物体表面的几何信息联系起来。

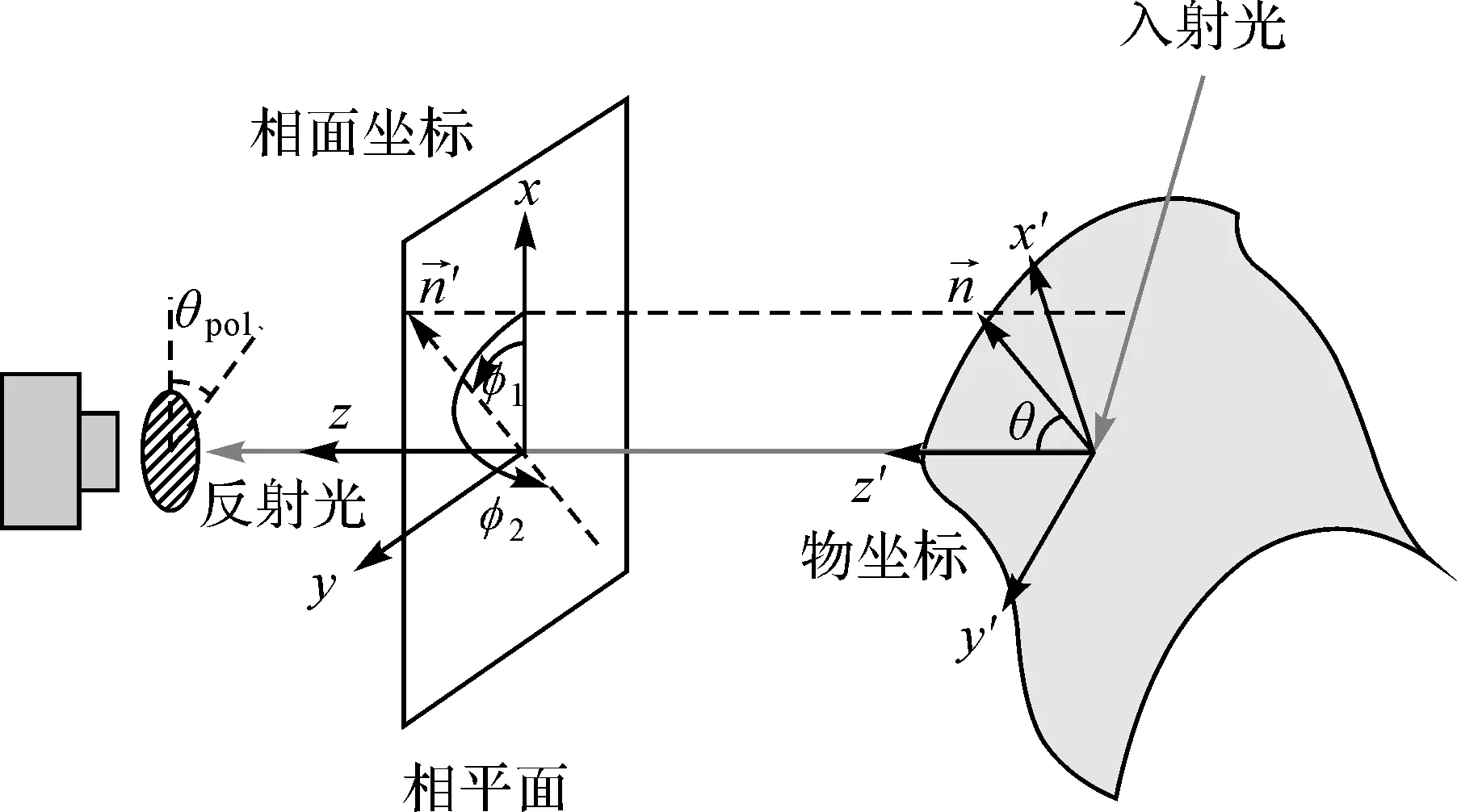
图1 反射偏振成像过程[25]Fig.1 Reflection polarization imaging process [25]

由菲涅尔原理可知，反射率会随着光矢量的振动方向变化而变化，因此将反射光通过偏振片，旋转偏振片，反射光的亮度会发生变化。将线偏振片置于相机镜头前，ν为偏振片透光轴与起始位置(参考位置)之间的夹角。光照强度I可表示为与偏振片旋转角度ν有关的正弦函数，如下式

(1)

式中，μ表示多波段偏振图像中的每一个像素点；λ表示对应的波段；Imax、Imin分别表示连续旋转偏振片时，CCD相机所观测到的最大光强与最小光强；φ表示反射光的偏振相角(angle of polarization，AoP)。

在波段λ下，采集N个偏振角度下的多波段偏振图像，分别记为I(ν1),I(ν2),…,I(νN),I(νi)表示第i次转动偏振片。因此第i次转动偏振片采集到的多波段偏振图像的每一个像素点处的强度值可以记为I(μ,λ,νi)=Ii(μ,λ)。则式(1)可以改写为

(2)

当偏振片旋转的次数N≥3时，式(2)变成一个正定系统，记为I=Ax，其中

(3)

(4)

1.2 基于偏振成像的三维重构原理

自然光属于非偏振光，但当自然光经物体表面反射后，反射光会变为部分偏振光。基于偏振视觉进行三维重建的关键在于通过偏振成像获取反射光的偏振状态，并将其与物体表面的几何信息联系起来，进而对法向量积分获得目标的表面三维形状。

通过分析反射光的偏振态可以获得目标表面法向量的方向参数，法向量主要受两个参数约束，即天顶角θd(zenith angle)和方位角αd(azimuth angle)。天顶角是指法线向量方向与z轴的夹角,方位角是指法向量在XoY平面的投影与x轴方向的夹角，如图2所示。

根据菲涅尔原理、折射定律及偏振度的定义可得到偏振度ρ与法线天顶角θd的关系为

(5)

方位角αd与偏振相角φ间有着如下的关系

(6)

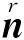
(7)

通过反射光偏振分析可以由偏振度和偏振相角分别求得法向量的天顶角θd和方位角αd(存在二义性)，进而确定物体表面每一点的法向量方向。物体表面的法向量反映的是目标表面的梯度信息，通过积分算法可以将物体表面的梯度信息转化为深度信息。

图2 法向量示意Fig.2 The normal vector schematic

假设物体的表面为Cartesian曲面(连续且闭合的曲面)，则物体表面的关系式可以用z=f(x,y)表示，表面某一点的法向量可以表示为

(8)

若目标的表面可以表示为函数z=f(x,y)，在XoY平面上的投影为区域Ω，则Ω上任一离散点(x，y)的梯度值为

(9)

由梯度值p(x，y)、q(x，y)到深度z的积分技术大致可以分两大类：局部积分算法和全局积分算法。其中，全局积分对噪声具有更好的鲁棒性，通过积分得到的表面更为平滑。全局积分算法将表面积分近似看作是一个最优化问题来处理，基本的代价函数为

(10)

2 基于多光谱偏振的天顶角和折射率的联合估计

利用偏振成像技术进行三维重建，关键在于求取目标表面所有点的法向量，即方位角和天顶角两个参数的求取。而在利用菲涅尔方程求解天顶角时，由式(5)可知，表面材料的折射系数n是求天顶角过程中一个极其重要的先验参数，而在许多实际应用中，如非合作目标的相对导航﹑陌生环境中物体探测等，目标表面材料特性通常是没有先验信息的。而仅利用菲涅尔方程，天顶角、偏振度和目标表面折射率间的关系是一个欠定方程，只知道偏振度无法获得天顶角。为解决这一问题，本文提出了基于多波段偏振成像的三维重建方法，利用柯西色散方程[26]将折射率展开为关于波长λ的有理函数f(λ)，待求解的是波长λ的系数。随着波长数量的增多，色散方程的数量将超过待求解变量的数量，使天顶角θd和折射率n的求解问题变成一个正定问题。将色散方程n=f(λ)代入表示天顶角θd和偏振度ρ之间关系的方程中，便转化为非线性最小二乘问题，利用线性搜寻或置信区间的方法便可以同时估计出天顶角θd和色散方程系数的最优解。得到θd，便可根据几何原理直接推导出法向量，可以同时获得物体的折射系数n和形状。

2.1 柯西色散方程

为了约束折射率在波长域的变化，注意到各种不同材质的折射率受材料色散方程的约束，本文采用柯西色散方程[26]用于优化框架。其描述折射率和波段之间的关系由式(11)表示。

(11)

式中，μ表示图像中的每一像素；λ表示波段；M表示系数总数。由式(11)可以看出折射率n仅与波段λ和色散方程系数ck(μ)有关，将折射率表示成波段的多项式函数，则折射率的求解问题变成了柯西色散方程系数的求解问题。

2.2 天顶角与折射率的联合优化

由式(2)、(3)和(4)可知，对于波段为λ的偏振图像的每一个像素点处的光强最大值和最小值可以求出，联合菲涅尔公式可得下式

(12)

式中，θd(μ)表示三维目标表面在像素μ处法线的天顶角；n(μ,λ)表示对应像素点处的折射率；F⊥(μ,λ)表示菲涅尔方程中垂直反射系数；F‖(μ,λ)表示菲涅尔方程中平行反射系数。

(13)

式中，N表示波段数，在此方程中加入柯西色散方程作为折射率的约束，利用这个约束，则上述损失函数将变成一个有M+1个变量的方程，待求解系数为θd(μ)和Ck(μ)，k=1,…,M，当色散方程系数的个数M使得M+1≤N时(N为波段数)，上述非线性最小二乘问题,可以利用线性搜寻或置信区间的方法求解。当天顶角求得后，利用1.2节中的积分函数(10)求得目标的三维形貌。并利用求得的柯西色散方程的系数ck(μ)求得折射率n。

3 试 验

为验证算法的有效性，搭建了偏振图像采集系统。以水平方向为参考方向，将相机镜头前的线偏振片分别旋转至0°、45°、90°及135°，获得 4个角度下的偏振图像并命名为I0、I45、I90及I135，并从每一幅偏振图像中分离出R、G、B 3个波段，这样每一个波段下都有4幅偏振图像，形成多波段偏振图像。本文分别以石膏圆柱、苹果、瓷碗和卫星模型为目标进行试验仿真。

文中的重构目标多为表面光滑、纹理信息单一甚至缺失的高反光非金属目标，这类目标容易受到杂散光的干扰，在目标表面形成耀光，进而影响后续三维重构的准确性。因此，对重构目标图像进行了基于多波段偏振的去耀光预处理。

理论分析与大量试验统计结果表明，目标表面的耀光、光斑等杂散光分量具有强偏振效应，可近似为部分线偏振光[27-28]；而漫反射分量起偏效应弱，近似为无偏光；同时，镜面耀光、光斑等杂散光在不同波段下有着不同的偏振态。因此，结合多波段偏振成像，提取有效的偏振光谱特征信息，可准确地判别漫反射分量与杂散光分量，从而高

效地抑制目标表面耀光、光斑等杂散光的不利干扰，进一步提高目标三维重构的视觉性能。

基于偏振多光谱的耀光去除预处理方法主要包含以下几个步骤。

第1步：构建联合偏振光谱特征向量进行杂散光检测，结合线偏振度及强度信息对杂散光区域进行有效准确的检测。

第2步：获取最大-最小偏振光谱差分图像(单通道无耀光图像)。经过分析，最大-最小偏振光谱差分图像仅与目标的漫反射分量有关，而与镜面杂散光无关。因此，利用0°、45°、90° 3个偏振方向的光谱差分图像，进行线性加权，生成单通道无耀光图像SSF，避免了耀光、光斑等杂散光的干扰，同时保留目标原有信息，能有效地引导后续杂散光的分离抑制。

第3步：基于最大-最小偏振光谱差分图像，实现杂散光分量分离。对于前两步中检测到的杂散光区域像素点，可在单通道无耀光图像SSF中寻求其强度值最接近的漫反射像素点，将此漫反射像素点原有的色彩强度作为杂散光像素点的漫反射色彩强度。基于以上策略，提出一种全局处理的最小二乘系数分解算法。该算法在SSF图像进行全局遍历搜寻，对检测到的杂散光区域实现有效引导反射系数分离，最终得到准确的杂散光分离结果。试验结果如图3—图6所示。

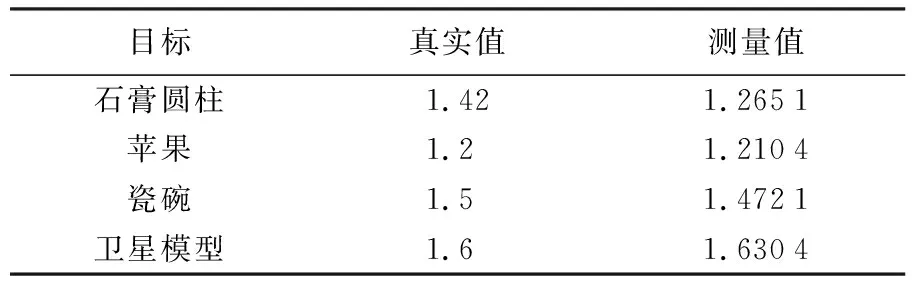
表1 折射率测量结果

图3 石膏圆柱Fig.3 Gypsum mold

需要说明的是：由于石膏圆柱表面没有耀光，因此没有去耀光试验结果。由试验结果可以看出，传统的双目三维重构方法由于需要丰富的纹理信息及对反光特性的依赖，对于高反光、纹理单一甚至缺失这一类特殊目标，如石膏圆柱、没有花纹的瓷碗、苹果等，无法提取丰富的特征点，从而导致重构结果出现大面积的数据空洞，不能得到目标完整的三维形貌，而基于多波段偏振的三维重构方法不需要依赖目标表面的纹理信息，仅需要利用偏振和光谱信息，得到了目标表面完整的三维信息，还同时得到了目标的折射率，实现了目标三维结构和折射率的联合估计。

图4 苹果Fig.4 Apple

图5 瓷碗Fig.5 Bowl

4 总 结

基于多波段偏振的三维重构方法同时利用图像的光谱信息和偏振信息，将摄影测量与机器视觉进行融合，实现了对高反光无纹理这一类特殊目标表面的完整三维重构，并成功解决了仅依靠菲涅尔理论无法实现天顶角和折射率的同时估计问题，扩大了三维重构的普适性，使得数字摄影测量具有更广泛的应用范围。并且本文利用光谱和偏振信息，对目标进行了去耀光预处理，进一步提高了三维重构的精度，并用仿真试验进行了验证。

图6 卫星模型Fig.6 Satellite model

参考文献：

[1] SONG Weitao, WENG Dongdong, LIU Yue, et al. Three-dimensional Reconstruction for Photon Counting Imaging Using a Planar Catadioptric Method[C]∥Proceedings of 2017 Conference on Lasers and Electro-optics Pacific Rim. Singapore: IEEE, 2017: 1-2.

[2] WANG Binquan, KONG Lingcheng, ZHAO Jianghai, et al. Design of Three-dimensional Reconstruction and Robot Path Planning Based on Kinect System[C]∥Proceedings of the 29th Chinese Control and Decision Conference. Chongqing, China: IEEE, 2017: 3829-3834.

[3] ZHANG Junning, PAN Wei, SHI Haobin, et al. Three-Dimensional Reconstruction Method Based on Target Recognition for Binocular Humanoid Robot[C]∥Proceedings of 2016 International Conference on Progress in Informatics and Computing. Shanghai, China: IEEE, 2017: 355-359.

[4] HONDA J, YOKOYAMA H, TAJIMA H, et al. Influences of 3D Aircraft Model to ILS Localizer[C]∥Proceedings of the 2016 10th International Conference on Complex, Intelligent, and Software Intensive Systems. Fukuoka, Japan: IEEE, 2016: 180-185.

[5] SUN Huabo, LUO Boren, YU Liling, et al. Mosaic Research with 3D LiDar Point Cloud of Civil Aircraft[C]∥Proceedings of the 2013 2nd International Symposium on Instrumentation and Measurement, Sensor Network and Automation. Toronto, ON, Canada: IEEE, 2013: 683-686.

[6] GODARD C, HEDMAN P, LI Wenbin, et al. Multi-View Reconstruction of Highly Specular Surfaces in Uncontrolled Environments[C]∥Proceedings of 2015 International Conference on 3D Vision. Lyon, France: IEEE, 2015: 19-27.

[7] ZHAO Yongqiang, YI Chen, KONG S G, et al. Multi-band Polarization Imaging and Applications[M]. Berlin, Heidelberg: Springer, 2016.

[8] RAGHEB H, HANCOCK E R. A Probabilistic Framework for Specular Shape-from-shading[J]. Pattern Recognition, 2003, 36(2): 407-427.

[9] KOSHIKAWA K. A Polarimetric Approach to Shape Understanding of Glossy Objects[C]∥Proceedings of the 6th International Joint Conference on Artificial Intelligence. Tokyo, Japan: Morgan Kaufmann Publishers Inc., 1979.

[10] GHOSH A, CHEN Tongbo, PEERS P, et al. Circularly Polarized Spherical Illumination Reflectometry[J]. ACM Transactions on Graphics, 2010, 29(6): 162.

[11] MIYAZAKI D, KAGESAWA M, IKEUCHI K. Transparent Surface Modeling from a Pair of Polarization Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 73-82.

[12] ATKINSON G A, HANCOCK E R. Multi-view Surface Reconstruction Using Polarization[C]∥Proceedings of the 10th IEEE International Conference on Computer Vision. Beijing, China: IEEE, 2005: 309-316.

[13] MIYAZAKI D, SAITO M, SATO Y, et al. Determining Surface Orientations of Transparent Objects Based on Polarization Degrees in Visible and Infrared Wavelengths[J]. Journal of the Optical Society of America A, 2002, 19(4): 687-694.

[14] MOREL O, GORRIA P. Polarization Imaging for 3D Inspection of Highly Reflective Metallic Objects[J]. Optics and Spectroscopy, 2006, 101(1): 11-17.

[15] STOLZ C, FERRATON M, MÉRIAUDEAU F. Shape from Polarization: A Method for Solving Zenithal Angle Ambiguity[J]. Optics Letters, 2012, 37(20): 4218-4220.

[16] ZHAO Yongqiang, WANG Miaomiao, YANG Guang, et al. FOV Expansion of Bioinspired Multiband Polarimetric Imagers with Convolutional Neural Networks[J]. IEEE Photonics Journal, 2018, 10(1): 1-14.

[17] MIYAZAKI D, SHIGETOMI T, BABA M, et al. Polarization-Based Surface Normal Estimation of Black Specular Objects from Multiple Viewpoints[C]∥Proceedings of the 2nd International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission. Zurich, Switzerland: IEEE, 2012: 104-111.

[18] DROUET F, STOLZ C, LALIGANT O, et al. 3D Reconstruction of External and Internal Surfaces of Transparent Objects from Polarization State of Highlights[J]. Optics Letters, 2014, 39(10): 2955-2958.

[19] ATKINSON G A, HANCOCK E R. Surface Reconstruction Using Polarization and Photometric Stereo[C]∥Proceedings of the 12th International Conference on Computer Analysis of Images and Patterns. Vienna, Austria: Springer, 2007: 466-473.

[20] SAMAN G, HANCOCK E. Refractive Index Estimation Using Photometric Stereo[C]∥Proceedings of the 18th IEEE International Conference on Image Processing. Brussels, Belgium: IEEE, 2011: 1925-1928.

[21] HUYNH C P, ROBLES-KELLY A, HANCOCK E R. Shape and Refractive Index from Single-View Spectro-Polarimetric Images[M]. Hingham: Kluwer Academic Publishers, 2013.

[22] KADAMBI A, TAAMAZYAN V, SHI Boxin, et al. Polarized 3D: High-quality Depth Sensing with Polarization Cues[C]∥Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 3370-3378.

[23] NGO T T, NAGAHARA H, TANIGUCHI R I. Shape and Light Directions from Shading and Polarization[C]∥Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 2310-2318.

[24] 平茜茜, 刘勇, 董欣明, 等. 基于偏振双目视觉的无纹理高反光目标三维重构[J]. 红外与毫米波学报, 2017, 36(4): 432-438.

Ping Xixi, LIU Yong, DONG Xinming, et al. 3-D Reconstruction of Textureless and high-Reflective target by Polarization and Binocular Stereo Vision[J]. Journal of Infrared and Millimeter Waves, 2017, 36(4): 432-438.

[25] AHMAD J E, TAKAKURA Y. Stereo-polarimetric Measurement of Pair of Mueller Images for Three Dimensional Partial Reconstruction[C]∥Proceedings of the 2006 14th European Signal Processing Conference. Florence, Italy: IEEE, 2006: 1-4.

[26] BORN M, WOLF E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light[M]. 7th ed. Oxford: Cambridge University Press, 1999.

[27] ZHAO Yongqiang, PENG Qunnie, YI Chen, et al. Multiband Polarization Imaging[J/OL]. Journal of Sensors,(2016)[2016-04-15].http:∥dx.doi.org/10.1155/2016/5985673.

[28] ZHAO Yongqiang, PENG Qunnie, XUE Jize, et al. Specular Reflection Removal Using Local Structural Similarity and Chromaticity Consistency[C]∥Proceedings of 2015 IEEE International Conference on Image Processing. Quebec City, QC, Canada: IEEE, 2015: 3397-3401.