基于激光扫描的立式金属罐容量计量方法
郝华东, 李存军, 刘 瑛, 施浩磊, 李曙光
(舟山市质量技术监督检测研究院, 浙江 舟山 316021)
1 引 言
立式金属罐(以下简称“立式罐”)是国内外大宗石油产品的主要储存器具,也是用于贸易结算的重要强制检定计量器具,其容量计量的准确性直接关系到国际间贸易的经济效益和国家计量信誉[1]。目前国际上立式罐的容量主要采用围尺法、光学参比线法、全站仪法等几何测量法[2~10]进行计量。围尺法作为国际仲裁检定的标准方法,需要搭建脚手架才能完成,属于高空作业;光学参比线法需要人工拉动移动式径向偏差测量仪,这两者均存在人工劳动强度大、安全系数差、测量效率低等缺点。全站仪法虽然测量效率有所提高,但是测量点数仍然有限、自动化程度不高。上述3种测量方法均是建立在 “立式罐是无变形的理想圆柱体”这一模型假设基础之上的,然而实际上由于建造水平或使用年限的影响,使得立式罐存在不规则变形,按照上述假设所建立的简化罐体模型与真实物理模型存在较大偏差,不能真正反映罐体实际三维几何特征,进而影响立式罐的容积测量准确度。此外,也有学者从事过容量比较法方面的研究[11],通过将已检定的立式罐作为标准罐,由于在高液位时罐底已不再发生弹性形变,无需考虑罐底变形的影响,故以高液位时圆筒部分作为标准容量,分批注入被测罐进行容量比较,从而确定罐底量、罐底变形量、浮顶质量等数据,最终产生新的罐容表。但该方法费时费水费力,不适用于大型立式罐容量计量。
三维激光扫描技术具有数据量大、测量速度快、精度高等突出特点[12,13],本文利用激光扫描方法测角测距的原理,建立一种基于激光扫描的立式罐容量计量方法,通过对获取的激光点云数据进行粗差剔除、滤波、精简、半径计算、截面积计算、体积计算等一系列数据处理过程,计算出不同液高下的半径值和容积值,通过与传统测量方法的结果比对,验证本文方法的有效性。
2 立式罐激光扫描容量计量
2.1 激光扫描系统工作原理
三维激光扫描系统主要由激光发射器、接收器、马达控制可旋转滤光镜、微处理器和软件控制电路、时间计数器等模块单元构成,通过控制传动装置的运动,完成对物体的全方位扫描。在完成距离D测量的同时,获取水平和竖直方向上的扫描角α、β;最后经过数据处理软件自动解算出目标物体表面的三维点云坐标数据。

图1 三维激光扫描坐标系统
在三维激光扫描坐标系统(如图1所示)中,任意一点P的坐标(xP,yP,zP)按式(1)计算。
(1)
对于标称容量50 000 m3以下的油罐,通常只需要一次扫描测量就能得到三维空间坐标信息;对于标称容量50 000 m3以上的大型油罐,为获取罐完整点云数据,至少需要3个扫描站点,同时在扫描测量时摆放标靶,标靶的坐标作为公共点,通过这些公共点可以将不同站点下的扫描数据经过坐标变换到同一个坐标系下,实现多站数据的拼接。
2.2 基于激光扫描的立式罐容积计算方法
2.2.1 立式罐容积计算数学模型
立式罐通常是由多个高度近似的圆柱形钢制圈板焊接而成,为保证罐体容积计算的准确性,将罐体点云数据沿高度方向分割为若干个小圆柱体,计算各小圆柱体的体积并叠加以获取总体积V。同时考虑温度、罐体倾斜度、液体静压力等修正,结合罐底量和附件体积,最终计算出总容积表。立式罐体积计算模型[2]为:
(2)
式中:Si为拟合小圆柱体底面面积;hi为所取小圆柱体高度;ΔVp为液体静压力修正值;ΔVA为罐内附件体积修正值;ΔVB为罐底量;ΔVL为罐体倾斜修正值。其中,小圆柱体的高度可根据需要进行设置,一般设为10~20 mm;小圆柱体底面半径采用最小二乘法进行拟合。
2.2.2 立式罐容积计算实施过程
立式罐容积计算的具体实施过程(如图2所示)如下:
1) 在小圆柱体的高度中心处,截取一定环高的点云数据,该环高的高度根据实际扫描点云数据的质量、疏密程度及所需测量精度进行设定;
2) 将其投影至同一水平面,进行粗差剔除、滤波、精简、半径计算等一系列处理,拟合计算出小圆柱体的底面面积,作为整个小圆柱体的截面面积。
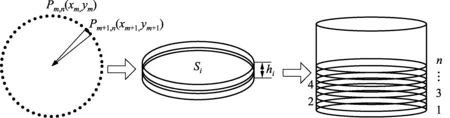
图2 立式罐体积计算图
2.2.3 立式罐点云数据处理算法
1) 点云数据粗差剔除与滤波
首先,采用3σ准则进行粗差的剔除[14]。对于某个给定的立式罐水平截面,假设ui为该水平截面上任一测量点半径(Ri)测量的残余误差,σ为该水平面上所有测量点半径测量的标准偏差,可以利用贝塞尔公式(式(3))进行计算,若满足式(4),则该测量点为粗大误差点,应删除。
(3)
(4)
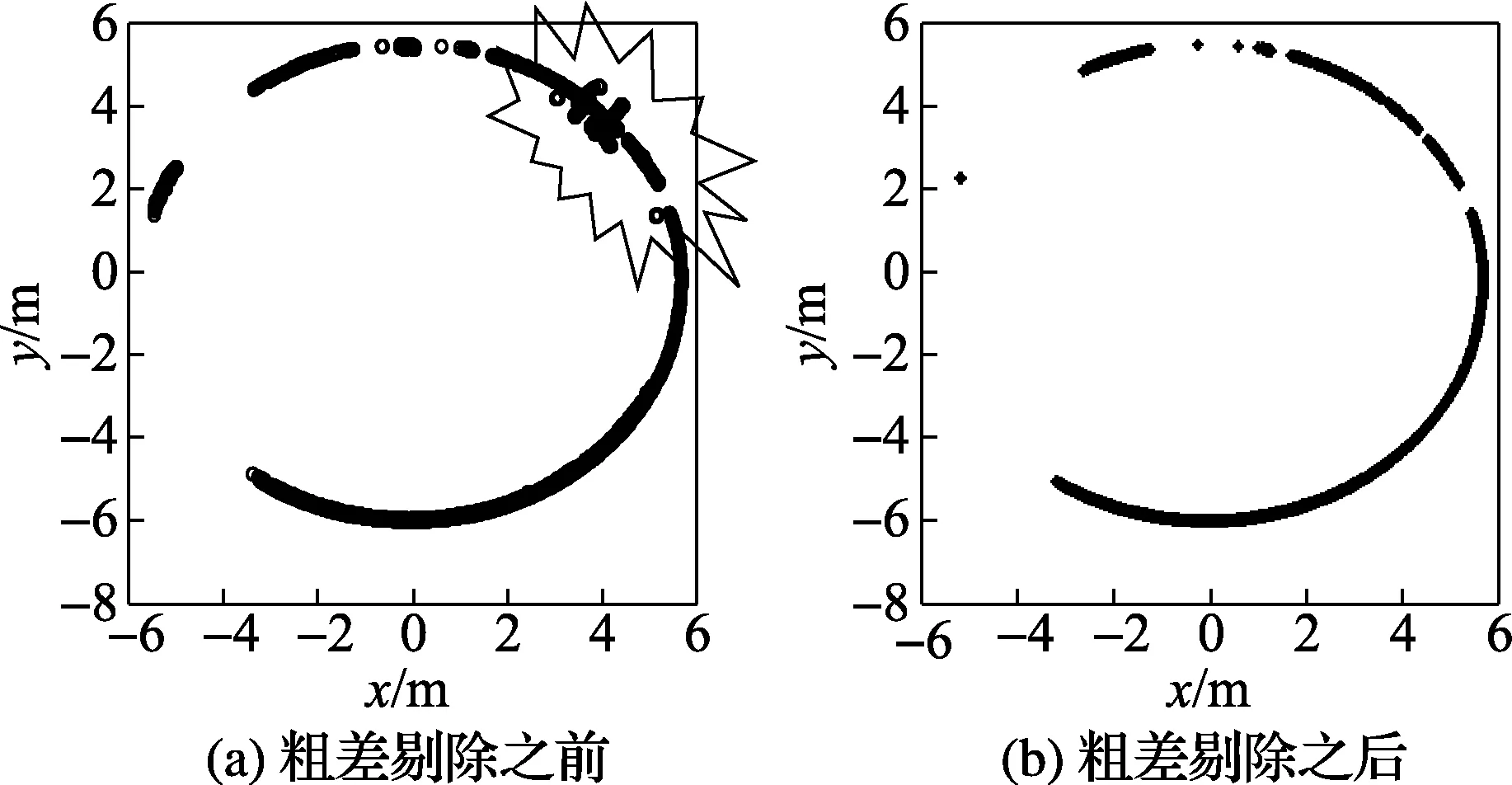
图3 粗差剔除前后对比图
然后,进行点云数据的滤波以实现噪声点剔除。中值滤波是以每个数据点为中心,设计一个包含奇数个数据点的滑动窗口,对这些奇数个数据点按照坐标值大小排序,用位于坐标值序列中间的坐标值代替窗口中心点的坐标值,可以较好地消除毛刺。作为一类根据高斯函数的形状选择权值的线性平滑滤波方法,高斯滤波能较好地保持原有形态。
2) 点云数据精简
由于获取的罐体点云数据量庞大,其中存在大量冗余数据,不利于后续建模,因此需要进行点云数据的精简。这里采用最小距离法进行点云精简,通过设定一个距离阈值,依次计算相邻两点之间的距离,若该距离小于设定的距离阈值,则将第二个删除。
3) 半径计算
从获取的点云数据中,提取每层圈板同一高度的点云数据,应用最小二乘法计算截面圆的半径[15]。最小二乘法是在随机误差为正态分布时,由最大似然法推出的最优估计算法,通过最小化误差平方和,寻找数据的最佳拟合函数。假设(xi,yi)为每层圈板测点坐标,(x0,y0)为所求圆圆心坐标,R为所求圆半径,d2为圈板测点与圆心距离平方和的均值,利用目标函数f分别对x、y、R求偏导,令其偏导为零,即可计算圆心坐标和半径(式(5)、式(6))。最小二乘法的优点在于其没有迭代过程,计算速度快。
(5)
f=(d2-R2)2
(6)
3 试验分析
为验证本文方法的有效性,分别设计立式罐容量计量的重复性与复现性试验、内测比对试验、不同标称容积的扫描试验等。试验中使用的三维激光扫描系统, 其扫描距离达187 m,扫描速度最高可达101.6×104点/s,距离25 m处扫描精度可达0.5 mm,点云最小间隔0.6 mm。
选取某石化公司一标称容量为1 000 m3的立式金属罐作为研究对象,该罐圈板总高度约为12.8 m,圈板直径约11.5 m,共有6层圈板。通过测量试验,对三维激光扫描系统的性能进行验证。
3.1 重复性测量试验
三维激光扫描系统的重复性测量试验是在不改变试验条件和仪器参数设置的前提下,对同一立式罐进行连续多次扫描,评判其扫描结果的一致程度。本文将该仪器架设于罐底中心位置(图4中S1处,其中左上角空心矩形代表的是计量板),按照分辨率为Middle、点云质量为High的模式,连续扫描6次。如图5所示,重复性测量试验半径计算标准偏差结果均小于0.04 mm,满足JJG 168—2005中“测量重复性均小于2 mm”的要求。
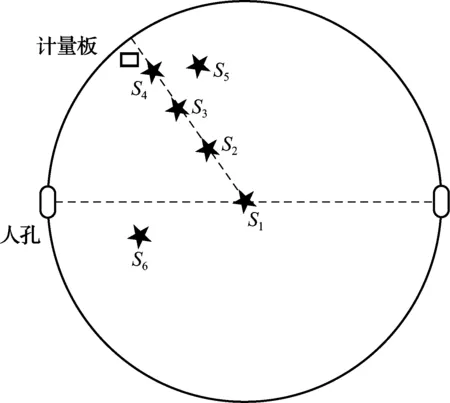
图4 测量试验设站分布图

图5 重复性测量试验半径计算标准偏差结果
3.2 复现性测量试验
三维激光扫描系统的复现性测量试验是在不同测量条件下(如不同扫描分辨率、不同点云质量、不同扫描位置等)对同一立式罐进行测量,评价其测量结果的一致程度。这里设计了两组复现性测量试验。
试验1是采用相同的仪器参数设置(分辨率为Middle、点云质量为High),将仪器变换6个不同的扫描位置(见图4中S1~S6处)进行测量试验,各圈板测量结果的标准偏差如图6所示。
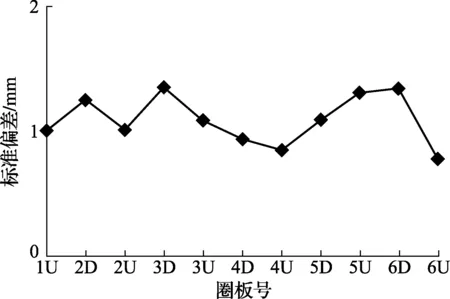
图6 复现性测量试验1半径计算标准偏差结果
试验2是将该仪器架设于罐底中心,设置扫描分辨率、点云质量的不同组合(见表1)分别进行测量,其测量结果的标准偏差如图7所示。

表1 三维激光扫描系统参数设置表
由图6和图7可知,复现性试验1和2各圈板半径测量的标准偏差分别小于1.5 mm和0.2 mm,满足JJG 168—2005中“测量复现性均小于2 mm”的要求;同时从图6中也可以看出,仪器的架设位置对半径的计算结果有一定影响。
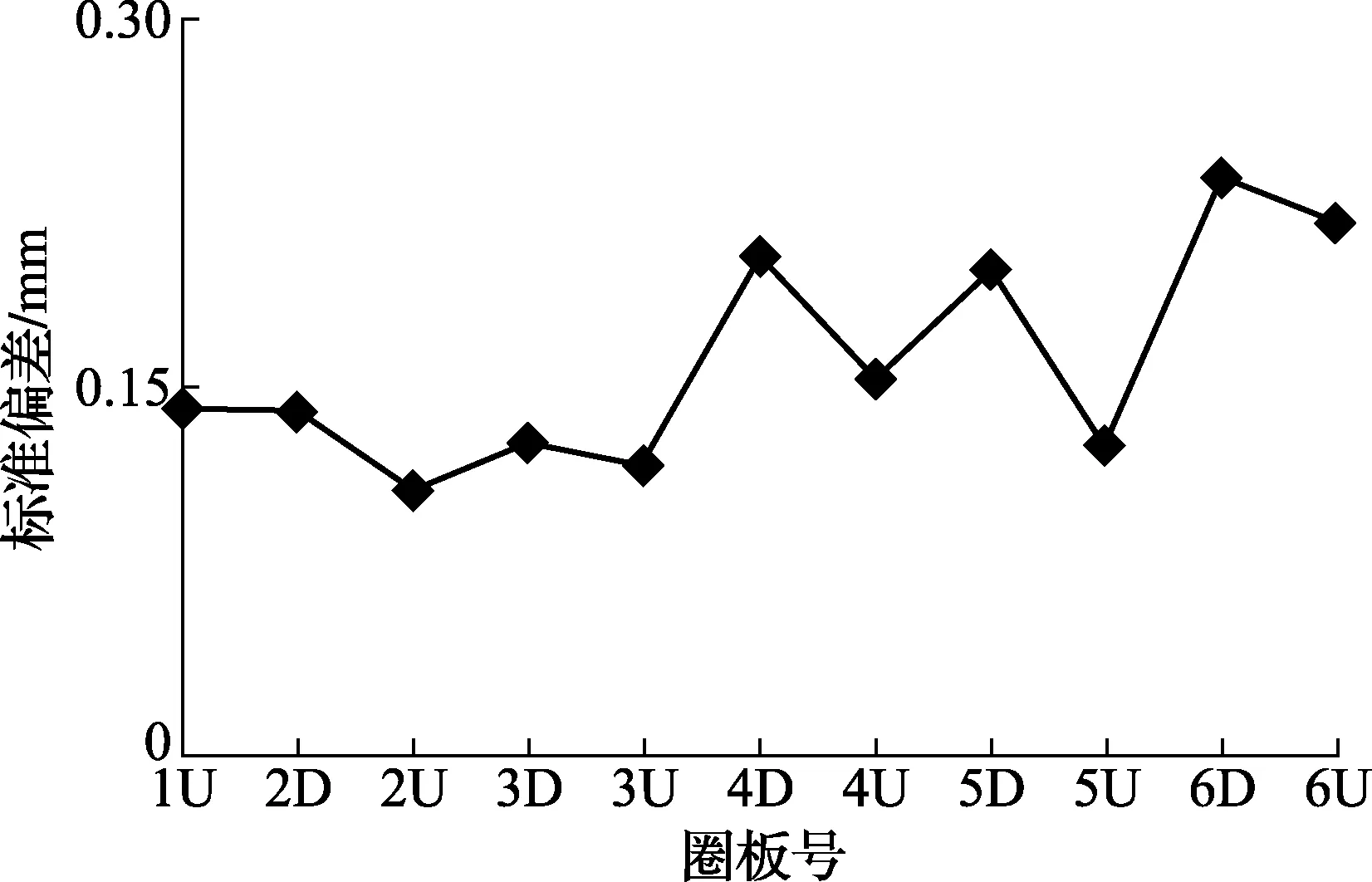
图7 复现性测量试验2半径计算标准偏差结果
3.3 与传统测量方法的比对试验
分别运用传统测量方法(围尺法+全站仪法)、本文方法,以该罐作为研究对象进行半径内测试验。 采用围尺法进行基圆(第一圈板3/4处)的测量,经钢卷尺修正、焊缝修正及板厚修正后得到基圆内周长,并换算成基圆内半径为5 739.6 mm,全站仪法所测的基圆半径为5 738.6 mm,用两者半径差值对全站仪法所测结果进行修正。本文方法半径由最小二乘法算得。对于罐底量、圈板高度、附件以及参考高度等数据不作比对范围,故在编制罐容表时,将底量和附件均视为相同。底量测量采用JJG 168—2005规程中的几何测量法,按照等面积法将罐底分成8个同心圆,与罐底8条等分半径相交确定64个测量点。然后将水准仪架设在罐底中心附近的稳定点上,用标高尺逐一立于各测量点、罐底中心点和下计量基准点上,由水准仪读出标尺读数,记录各测量点的标高。然后通过积分运算得出底量。本文方法与传统测量方法的半径测量标准偏差值均在±2.0 mm之内(如图8所示),同时,提取同一高度下两种测量方法获取的容积,两种方法的容积测量相对偏差均小于0.1%(如图9所示),满足JJG 168—2005中的测量要求。

图8 1 000 m3半径测量标准偏差
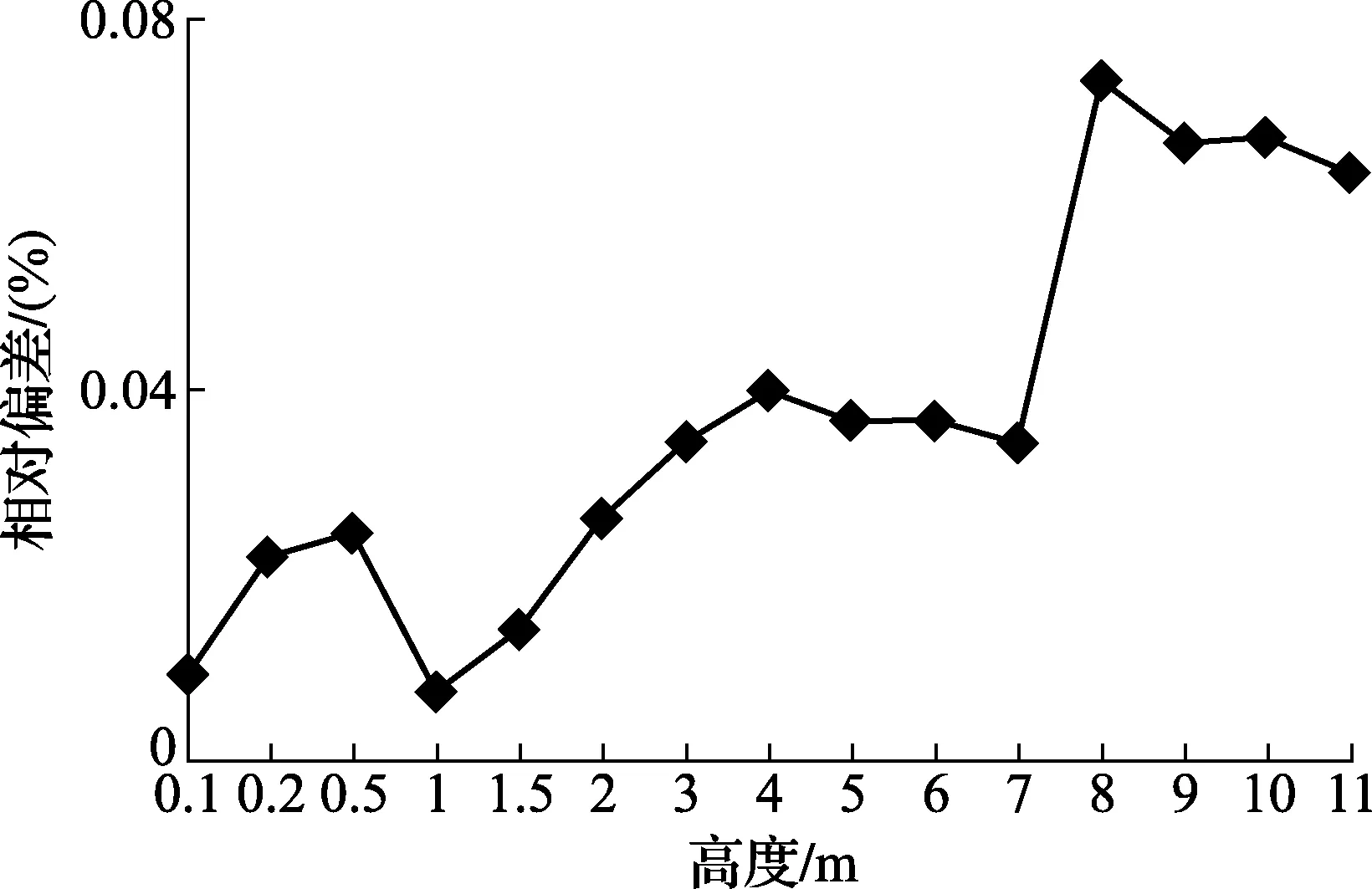
图9 1 000 m3容积测量相对偏差
再选取容量分别为2 500 m3、5 000 m3的立式罐分别进行相同的测量试验,结果如图10~图13所示,除了5 000 m3的立式金属罐第5、7、8圈板外,2种方法其他圈板的半径测量标准偏差均在±2.0 mm之内,容积测量的相对偏差均小于0.1%,能够满足JJG 168—2005中的测量要求。
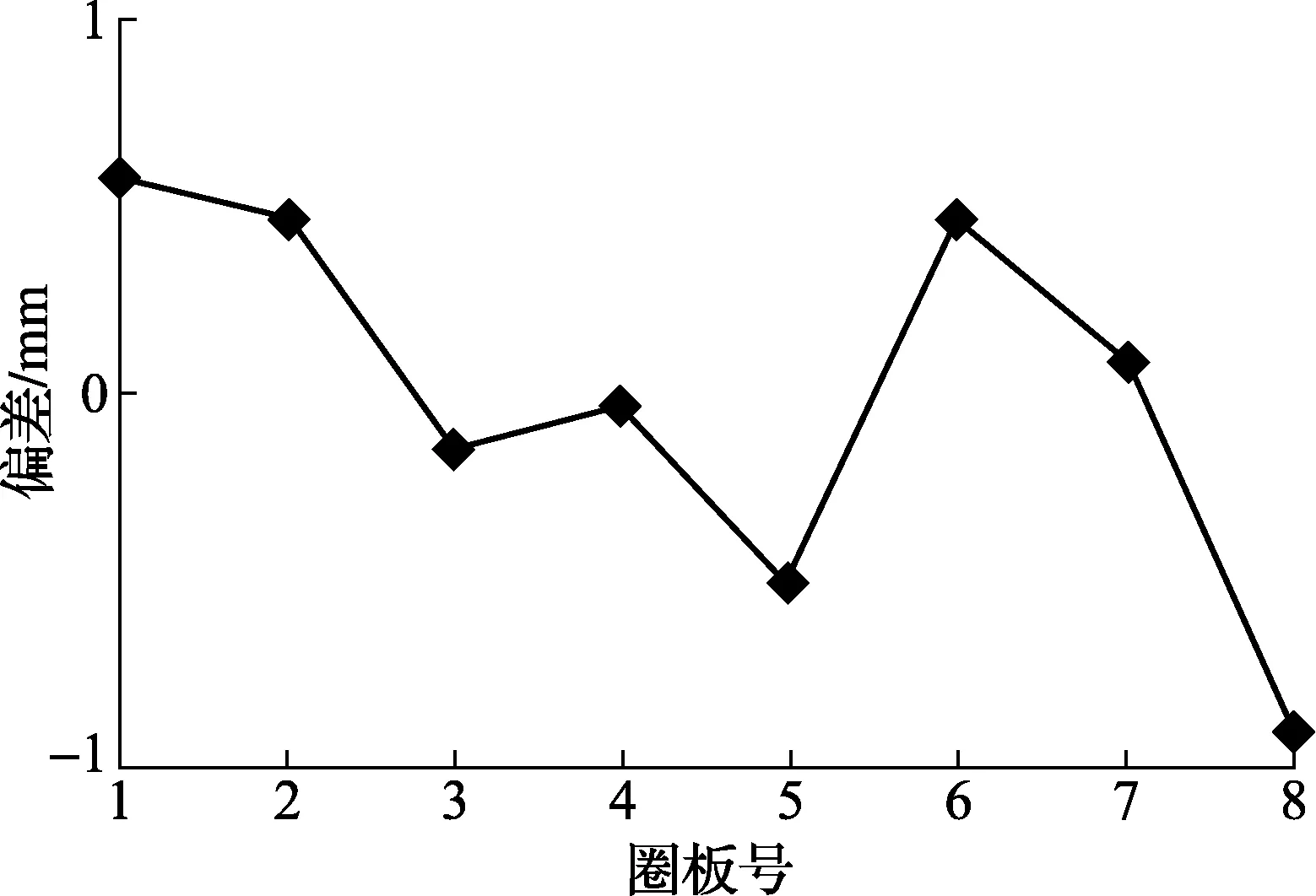
图10 2 500 m3半径测量偏差
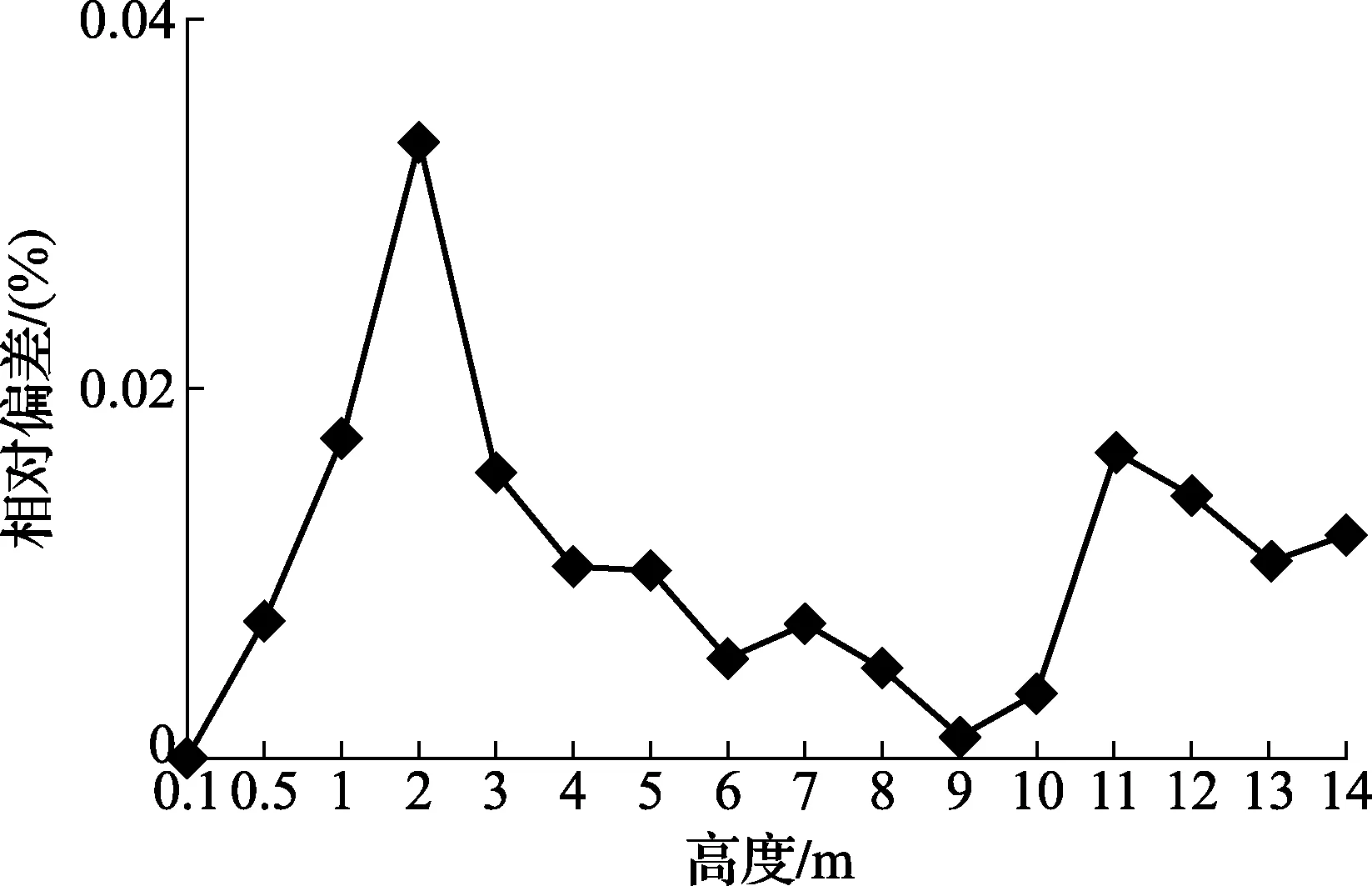
图11 2 500 m3容积测量相对偏差
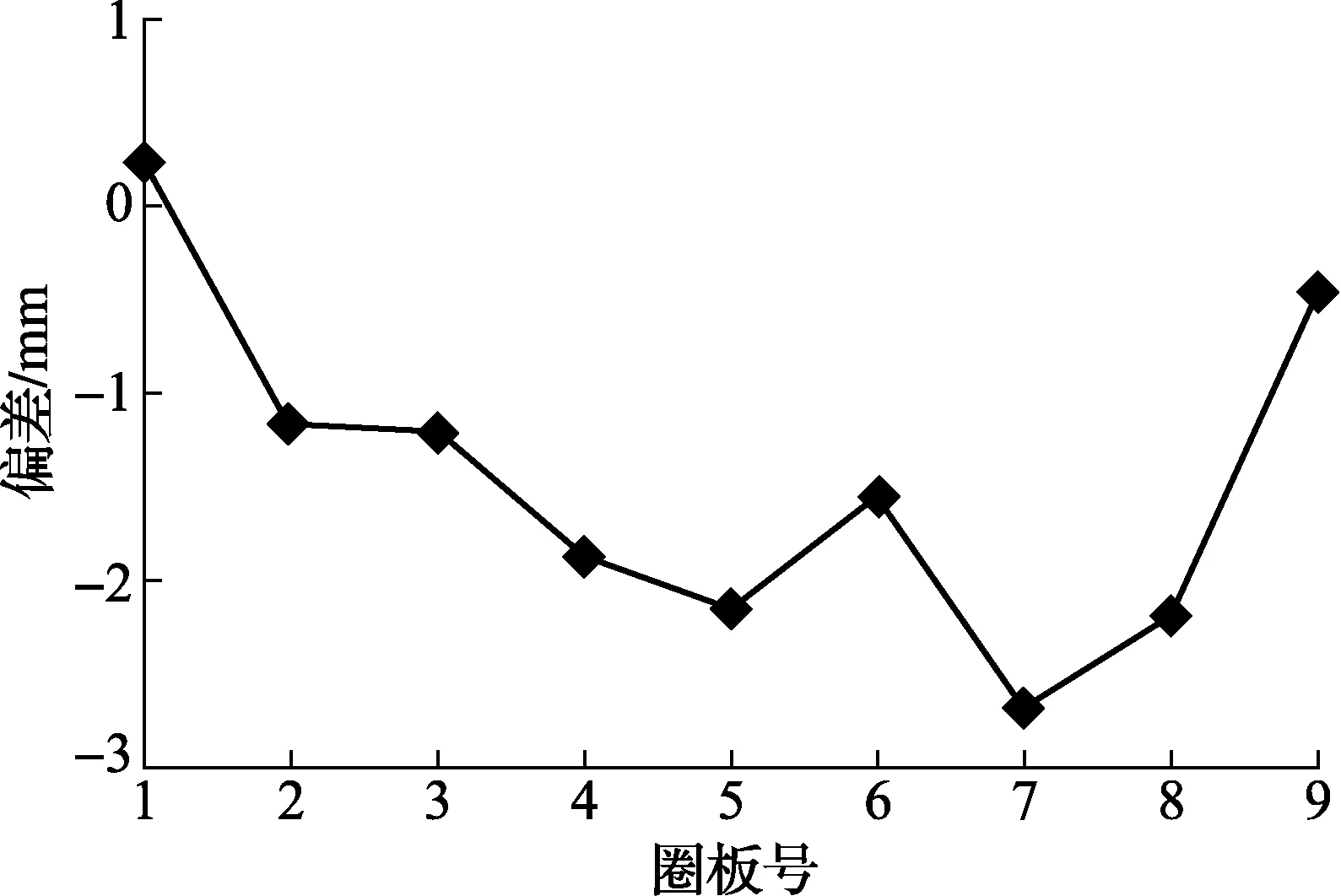
图12 5 000 m3半径测量偏差
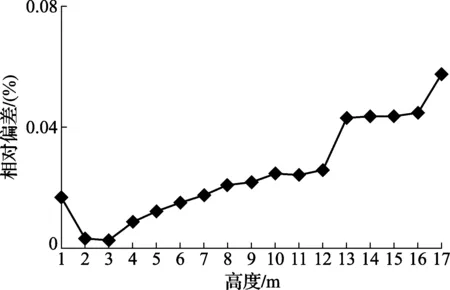
图13 5 000 m3容积测量相对偏差
4 结 论
综上所述,本文建立了一种基于激光扫描的立式罐容量计量方法,首先利用激光扫描测距测角原理建立罐体三维点云数据模型,通过对激光点云数据分析计算水平截面积,然后沿垂直高度方向积分,自动计算出不同液高下的容积值。该方法打破了传统测量方法无法对不规则罐体准确建模的限制,能够有效提高立式罐容量计量的准确度和工作效率。试验结果表明该方法具有良好的重复性和复现性。通过3种不同标称容量的立式罐比对测量试验,表明该方法测得的圈板半径标准偏差在可接受范围之内,计算的容积相对偏差均小于0.1%,满足JJG 168—2005中的测量要求。
[参考文献]
[1] 刘子勇.容量计量[M].北京:中国计量出版社,2009:11.
[2] JJG 168—2005 立式金属罐容量计量检定规程[S]. 2005.
[3] ISO 7507—1—2003 Petroleum and liquid petroleum products volumetic calibration of vertical cylindrical tanks[S].2003:6-11.
[4] ISO 7507—2—2005 Petroleum and liquid petroleum products volumetric calibration of vertical cylindrical tanks part2:optical reference line method[S]. 2005:6-16.
[5] ISO 7507—4—2010 Petroleum and liquid prtroleum products volumetric calibration of vertical cylindrical tanks part4:Internal electro-optical distance-ranging method [S]. 2010:1-7.
[6] OIML R71 2008 Fixed storage tanks General requirements[S]. 2008:11-18.
[7] 廉育英, 刘子勇, 何力, 等. 立式金属计量罐大容量的新测量方法[J].计量学报, 1988,9(4):241-247.
[8] 王金涛, 刘子勇, 张珑, 等. 基于点云分析的大型立式液态石化产品储罐容量计量方法研究[J].计量学报, 2011, 32(2):110-113.
[9] Nosach V V, Belyaev B M. The Calibration of Large Vertical Cylindrical Tanks by a Geometrical Method [J].MeasurementTechniques,2002,45(22):1153-1157.
[10] 吴斌,丁文,杨峰亭,等. 非正交轴系全站仪坐标测量系统误差分析技术研究[J]. 计量学报, 2017,38(6):661-666.
[11] 佟贵新, 郑鹤, 彭元博, 等. 容量比较法检定罐容案例分析及研究[J]. 中国计量, 2017, (7):104-105.
[12] 赵庆阳. 三维激光扫描仪数据采集系统研制[D]. 西安:西安科技大学, 2008.
[13] 魏凯, 宋述古, 刘子勇. 基于三维激光扫描原理的球形罐容量计量方法研究[J]. 计量学报, 2015, 36(6):607-609.
[14] 罗大兵, 高明, 王培俊. 逆向工程中数字化测量与点云数据处理[J].机械设计与制造, 2005, (9):56-58.
[15] 佟林, 王金涛, 刘子勇, 等. 基于光电内测法的立式罐容量计量中圈板半径拟合算法的研究[J]. 计量学报, 2011,32(6):522-525.

