支撑共振法测量液体密度的研究

韩立立, 曹 旭, 王 岍, 王 杰, 齐 凯, 李书光

(1. 中国石油大学(华东), 山东 青岛 266580; 2. 中国科学技术大学, 安徽 合肥 230029)

1 引 言

在工业生产和社会生活的众多领域,液体密度的测量有着重要的意义。根据测量原理的不同,密度测量主要可以分为2类[1,2]:一类是基于密度基本公式的直接测量,如密度瓶法、密度计法、液体静力天平法;一类是利用密度量与某些物理量关系进行间接测量,如振动法、射线法和声学法。振动法主要是通过测定液体流过振动管时的共振频率进而求出待测液体的密度,现有的测量装置往往需要和电磁线圈或者编程电路等相结合,测量结构比较复杂,成本较高,而且易受环境影响[3]。

本文借鉴实心棒状材料杨氏模量横振动方程的求解方法,对内部含流体管状材料横振动方程进行近似求解,得到密封管内液体密度的测量公式,实验操作简单,测量成本低,受气压、湿度等环境影响较小,而且有较高的精度。实验选取蒸馏水和质量浓度分别为0.1、0.3、0.4 g/mL的蔗糖溶液进行测量,测量得到的液体密度值与理论值之间的相对误差在3%以内,并分析了实验误差的来源以及减小误差的措施。

2 测量原理

2.1 液体密度测量原理

对于内部含有流体的管状材料,其做微小横振动时满足横振动Housner方程[4]:

(1)

式中:EI为管道横截面的抗弯刚度;ρ为液体密度;A为管道的横截面积;v为液体流速;m为空管子的单位长度质量;y为管材距端面距离为x处的横截面y方向的位移;t为时间。

如果控制液体的流速为0,即v=0,则:

(2)

对式(2)用分离变量法[5]求解,得到管状材料内部液体密度为:

(3)

式中:E为管状材料的杨氏模量;D为管道外直径;d为管道内直径;f为含液体试样的基频;L为管长。因此,液体密度测量的关键是对基频的测量。

2.2 基频测量装置及原理

在支撑共振法测量材料的共振频率的过程中,功率函数信号发生器发出500～2 000 Hz的正弦信号到发射换能器,将电信号转换为机械振动并激发试样棒受迫振动,另一端的接收换能器再将沿试样传过来的机械振动转换为电信号,经过处理放大后在示波器上显示出来[6],当发生共振时,振动波形的幅度最大。测量装置示意图如图1所示。

图1 含液体管基频测量装置示意图

对式(2)进行数值求解可以得到试样在做基频振动时存在2个节点,节点位置分别距端面0.224L和0.776L[6]。但由于节点处的试样很难被激振和拾振,振动振幅接近零,无法直接测量基频。而且考虑到支撑架对试样还有阻尼作用,为了消除这一系统误差,一般都是采用在节点两侧选取不同的点对称支撑,测量出节点附近点的共振频率后,拟合出相应的共振频率曲线方程,进而求出试样的固有频率。

3 测量材料及方法

3.1 材料与仪器

实验材料主要为:黄铜管、蒸馏水、蔗糖(AR 分析纯,国药集团化学试剂有限公司生产)。

实验仪器:DCY-3D型功率函数信号发生器、动态杨氏模量测定仪(主要包括底座、激发和接收换能器)、TDS1001型示波器、高精度光电天平(最小分度0.1 mg)。

3.2 方法与步骤

用光电天平称量一定质量的蔗糖,根据相应浓度计算比例加入蒸馏水,溶解配置成浓度分别为0.1、0.3、0.4 g/mL的蔗糖溶液。测量黄铜试样管的长度、内外直径及质量,3次测量后取平均值。

将试样管内部装满蒸馏水,使用很小的一段热缩管和塑料薄膜将端口密封,在将试样管两端对称的平放于激发换能器与接收换能器上,支撑点距试样管端口10 mm。

信号发生器发出正弦信号经过激发换能器,电信号转换为机械振动并迫使试样管发生振动,接收换能器接收振动并转换为电信号,再传输到示波器上显示出相应波形。调节信号发生器输出信号频率,当发生共振时,示波器上的波形幅度最大,记录此时正弦信号的频率即为对应支撑点的共振频率。移动换能器的位置,测量支撑点距试样管端口分别为15,20,25,30,35,40,45,50,55,60 mm处试样的共振频率,记录相应数据。将蒸馏水换为不同浓度的蔗糖溶液,重复上述测量步骤。

4 测量数据及处理

4.1 测量数据

实验使用的黄铜试样管参数如表1所示。

表1 黄铜管参数测量值

用支撑共振法测量内部充满不同溶液时黄铜试样管的共振频率如表2所示。

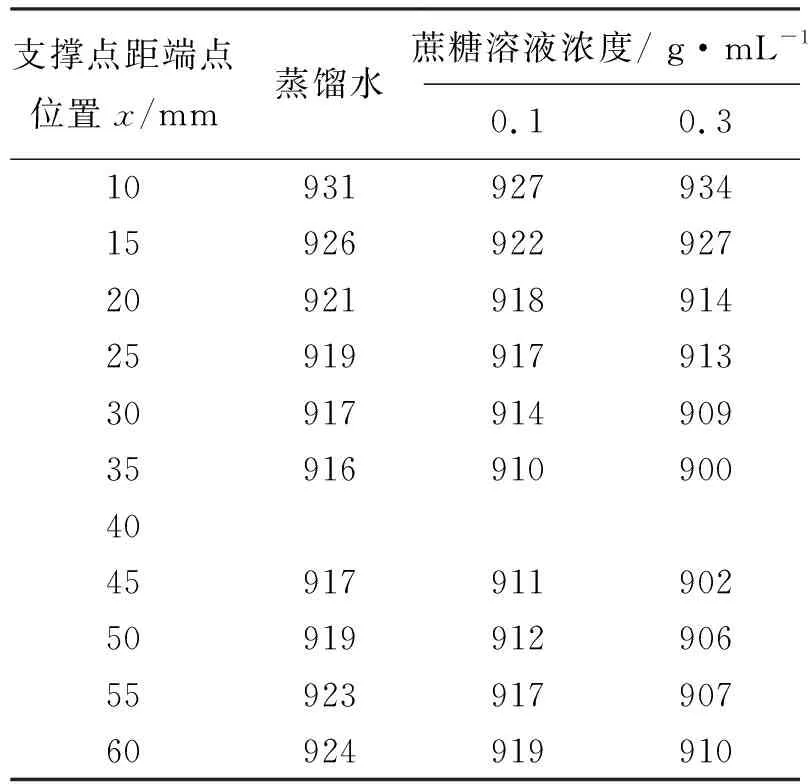
表2 黄铜试样管充满不同浓度溶液时的共振频率 Hz

4.2 测量数据处理

利用Origin8数据处理软件分别对4种振动频率数据进行最小二乘法多项式拟合[7,8]。经过多次拟合发现,当拟合次数为3次时,实验值与理论值最为接近,所以将拟合次数设为3次,得到的拟合图像分别如图2～图5所示。

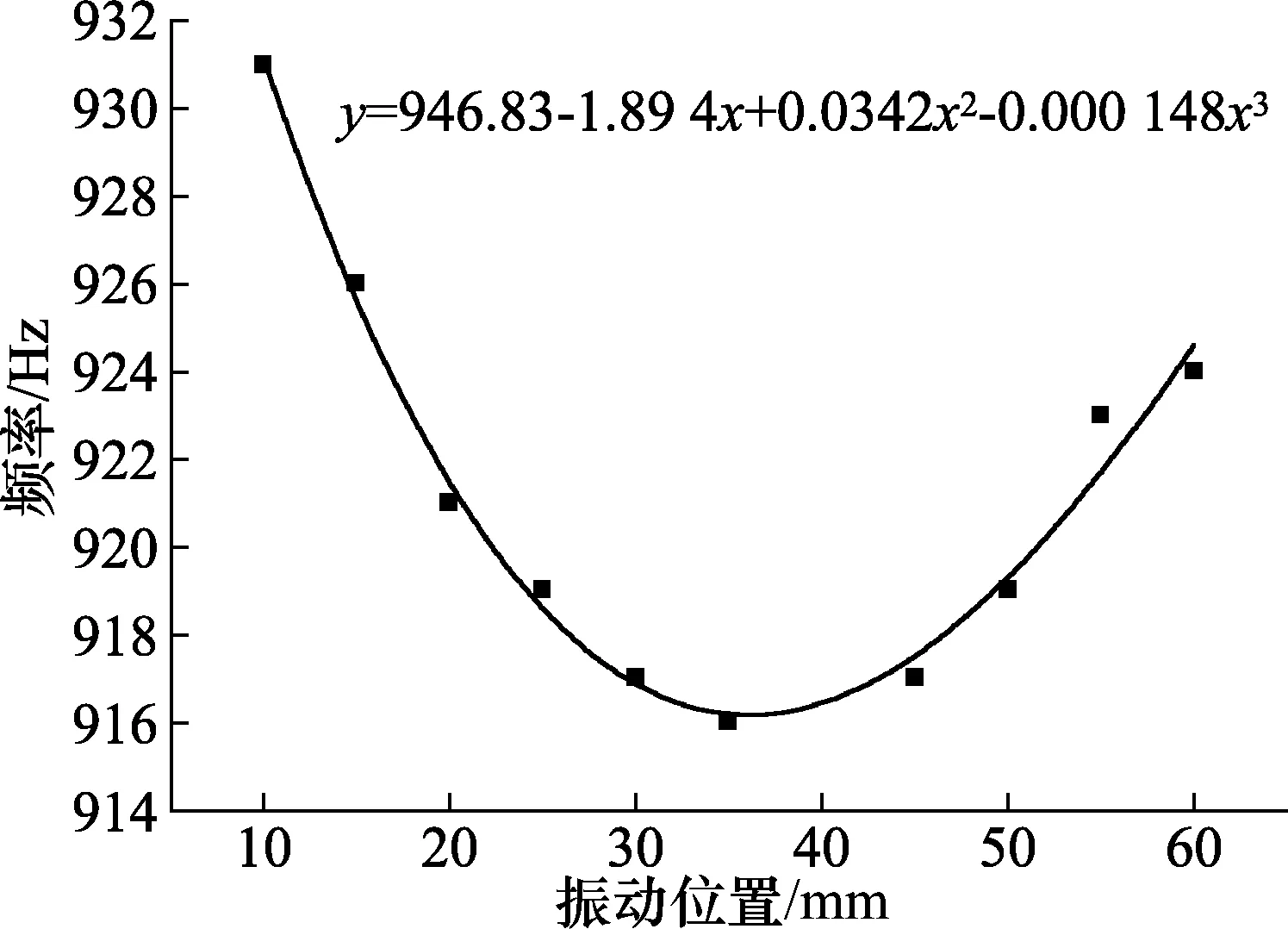
图2 充满蒸馏水黄铜管振动位置频率拟合曲线

图3 充满0.1 g/ml蔗糖黄铜管振动位置频率拟合曲线

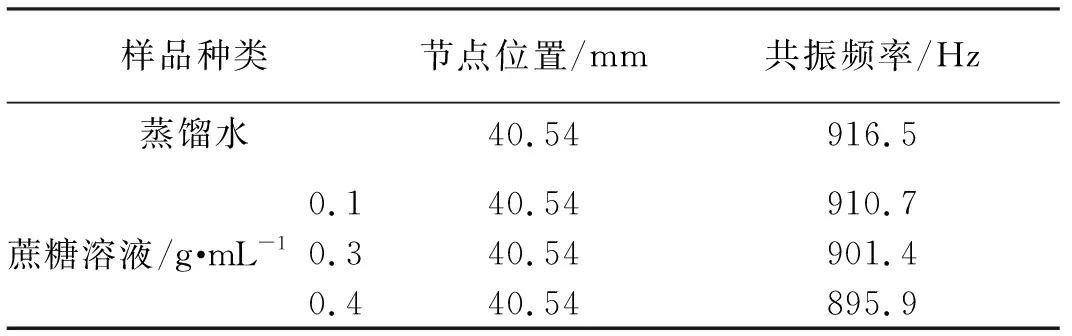
将节点位置代入拟合多项式,求出节点处的共振频率(基频),具体结果如表3所示。

已知实验用黄铜管的杨氏模量为E=104 Gpa(生产厂家提供),将黄铜管的L、m、D、d、A、E以及f代入式(3)可以计算得到相应液体密度如表4所示。

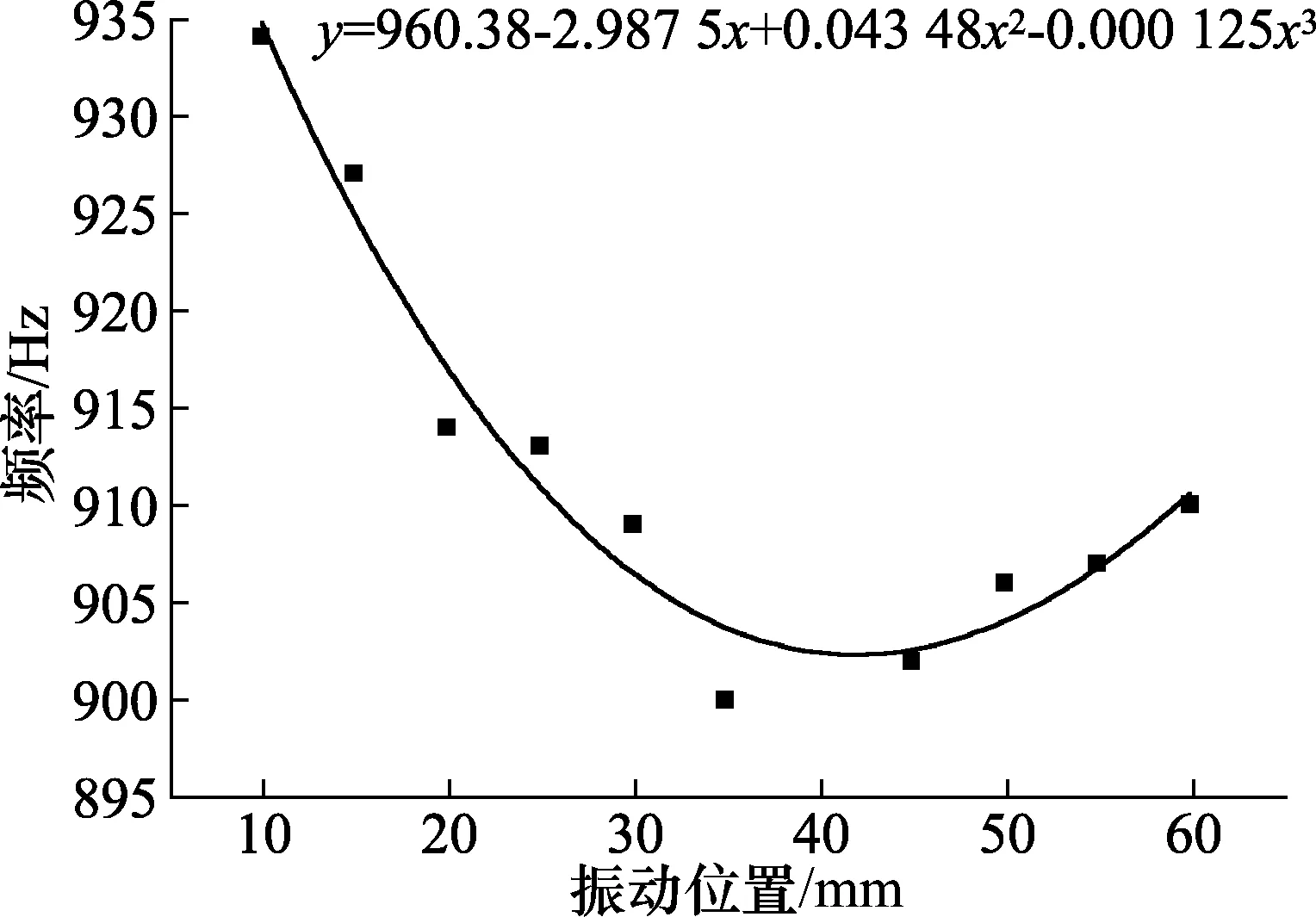
图4 充满0.3 g/ml蔗糖黄铜管振动位置频率拟合曲线

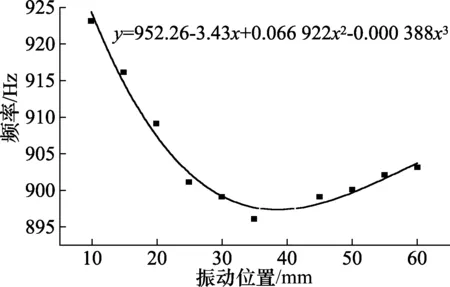
图5 充满0.4 g/ml蔗糖黄铜管振动位置频率拟合曲线

样品种类节点位置/mm共振频率/Hz蒸馏水40.54916.50.140.54910.7蔗糖溶液/g·mL-10.340.54901.40.440.54895.9

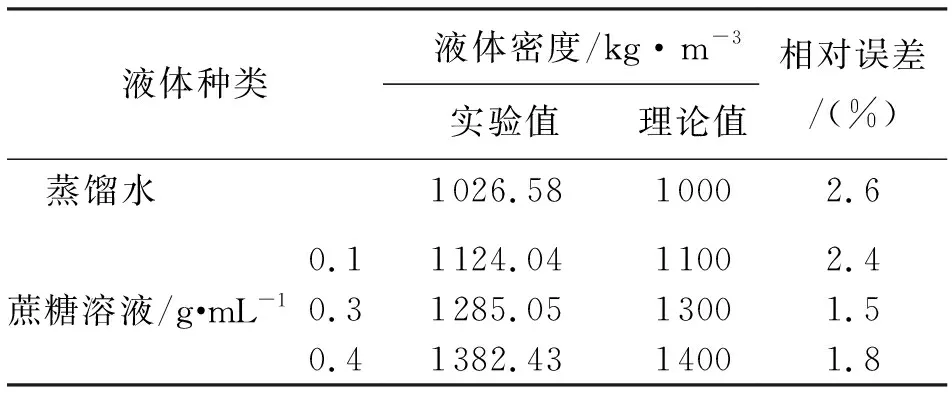
表4 液体密度测量结果及相对误差

5 测量误差分析

导致实验结果误差的原因主要从以下几点考虑:1)由于试样管不断受迫振动,内部流体流速很难保持零的状态,因此会产生一定的误差;2)对管内液体进行密封时,由于封口材料具有一定的质量,导致试样管单位质量的测量计算出现误差,因此,用支撑共振法测量液体密度应该还有一项修正项[7],但由于受实验次数限制,修正项需要大量的测量才能得出,这对实验结果产生较大的误差;3)最终结果也会受到测量过程中的各种因素的影响[8～11]。

在黄铜棒的相关参数测量的过程中,内外径d、D的及长度L的测量引起的误差较大,下面分别对这几个参数测量的不确定度进行分析和计算。首先计算直接测量的内外径及长度的不确定度,直接测量量k的标准不确定度A类分量用算术平均值的标准差估算公式计算(置信概率p为0.683),即:

(4)

其中:n为在相同条件下测量的次数,tp为与测量的次数有关的比例系数[9], 当n=6时,tp取1.11[10]。

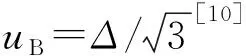
合成标准不确定度计算方法为:

(5)

而间接测量物理量密度的不确定度由内外径以及长度的不确定度决定。由统计理论可推出:

(6)

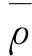
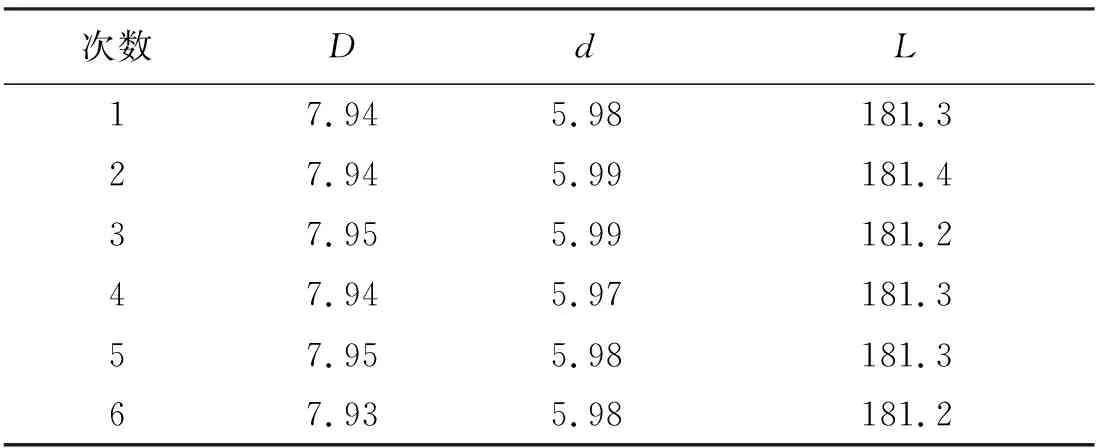
表5 相关参数多次测量数据 mm

将表5中的实验数据代入式(4)～式(6)中,联立求解得到相关物理量及最终结果密度的不确定度如表6所示(以0.3 g/ml的蔗糖溶液为例)。

表6 铜管参数及液体密度的不确定度

液体密度的最终测量结果为:

ρ=(1285.1±24.6) kg/m3,p=68.3%

相对合成不确定度为:

6 结 论

通过对流体管道Housner方程的近似求解,得出密封管内液体密度与管壁的基振频率之间的关系式,进而通过测量基振频率求得液体密度,这是一种合理可行的测量方法。与传统振动法测量液体密度相比,该实验方法成本低、操作简单、受环境影响小,有一定的推广应用价值。另外,本文对不同液体进行了多次测量,并且对测量数据进行了误差分析和不确定度处理,有利于进一步在实验上对共振法测量液体密度进行研究。

[参考文献]

[1] 李兴华. 密度计量[M]. 北京:中国计量出版社, 2002.

[2] 陈智军，韩超，陈涛, 等. 基于人工神经网络的乐甫波液体密度粘度并行检测研究[J]. 计量学报, 2017, 38(6): 721-724.

[3] 魏新华, 龚家伟, 喻谷源, 等. 振动管式液体密度传感器机理的研究[J]. 农业机械学报, 2011,32(5):89-93.

[4] 张悉德, 杜涛, 张文, 等. 输送流体管道Housner方程的修正[J]. 应用数学与力学, 1993, 14(2):147-149.

[5] 王龙, 李东霞. 动态法测量杨氏模量的理论分析与Matlab辅助研究[J]. 大学物理, 2015, 34(10):39-42.

[6] 韩立立, 王岍. 支撑共振法测量固体材料杨氏模量[J]. 计量技术, 2013, (11):20-22.

[7] 李伟明. 有限元模型修正方法及自由度匹配迭代技术研究[D]. 上海交通大学, 2011:2-13.

[8] 顾英姿, 陈朝晖, 许常红, 等. 液体静力称量法液体密度测量及其不确定度评定[J].计量技术, 2006, (6):8-11.

[9] 虞仲博, 屠全良. 牛顿环实验等精度测量及其不确定度的评定与表示[J]. 物理实验, 2000, 20(5):17-19.

[10] 刘才明. 大学物理实验中测量不确定度的评定与表示[J]. 大学物理, 1997, 16(8):21-23.

[11] 余学锋, 于杰, 王柯, 等. 基于证据理论的测量不确定度评定与分析[J]. 计量学报, 2017, 38(2): 252-256.