液体密度量传中大气压强影响的研究

张竟月, 王金涛, 时文才, 刘 翔,李占宏, 佟 林, 马鑫钰

(1. 中国计量科学研究院, 北京 100029;2. 中国计量大学, 浙江 杭州 310018)

1 引 言

密度作为液体物质的一种物理性质,在贸易交接、食品安全、环境保护、物质检定以及科学研究等各个领域发挥着重大作用。国际计量委员会(CIPM)在关键比对CCM.D-K2 “液体密度基准的比对”中,提出密度范围由600 kg·m-3到1 600 kg·m-3的几种液体作为密度标准液体,并给出在特定温度下各个密度标准液体的密度值[1,2]。中国计量科学研究院参考CIPM关键比对CCM.D-K2提出使用水、正十二烷、正十五烷和四氯乙烯几种液体作为密度标准液体。固体密度基准是由单晶硅球制成,固体密度基准采用绝对测量法建立,它的量值直接溯源到质量和长度。在密度量值传递体系中,液体基准由固体基准传递得到,即标准液的密度值通过载有单晶硅球的静力称重装置测量得到[3～8],其相对测量不确定度要求小于6×10-6。在如此高的精度要求下，大气压强对液体密度的影响不可忽略。为了研究并且修正大气压强对密度标准液密度值的影响,需要在低压下对这些液体的压缩系数进行测量。

压缩系数是表征液体可压缩性大小的参数。测量液体压缩系数一般是测量压强带来的体积变化或者密度变化。测量压强带来体积变化的难度在于微小体积变化的测量,同时还要考虑容器的压缩系数。这类测量方法为了方便测量体积变化,往往施加较大压强,难以测量液体低压下的压缩系数。例如测量油类体积模量的装置,测量压强通常在10 MPa以上[9,10]。Pena和Tardajos使用汞柱、毛细管和压强计等器具,测量了在0～2 MPa苯和各类烷烃液体的压缩系数。测量压强带来密度变化的难度在于密度值的精密测量,但基于振动频率原理的振动管密度计可以实现高精度测量液体密度,经过标准密度物质校准之后可以准确测量待测液体的密度值。为了测量密度标准液在低压下的压缩系数,提出一种基于液体密度和压强间的关系,使用高精度振动管密度计测量低压下液体压缩系数的方法。

2 理论分析

2.1 低压对液体密度的影响

通常使用谐振法测量液体密度。谐振法是基于振动管的振动频率与被测液体密度有一定函数关系的原理,通过测量振动频率来计算液体密度的一种方法。基于谐振法的振动管密度计原理如图1所示。在恒温容器中采用光学传感器测量振动管和参比管的振动周期,两者周期之比为振荡值τ。再通过液体密度ρ与振荡值τ之间的关系来确定待测液体密度。考虑到待测液体的粘度较小可以忽略,对于振动管密度计来说,待测液体密度值ρ与振荡值τ的简化关系如下:

ρ=Aτ2-B

(1)

图1 振动管密度计示意图

施加额外压强后,振动管密度计的参数A和B发生了变化。如果继续使用密度计在标准大气压下的参数A和B,最后密度计示值将会出现错误。为判断参数是否发生不可忽略的改变,使用在标准大气压强下校准的密度计测量纯水在施加较小压强后的密度值。测量纯水在施加压强到达0.3 MPa的密度值,测量结果如图2所示。

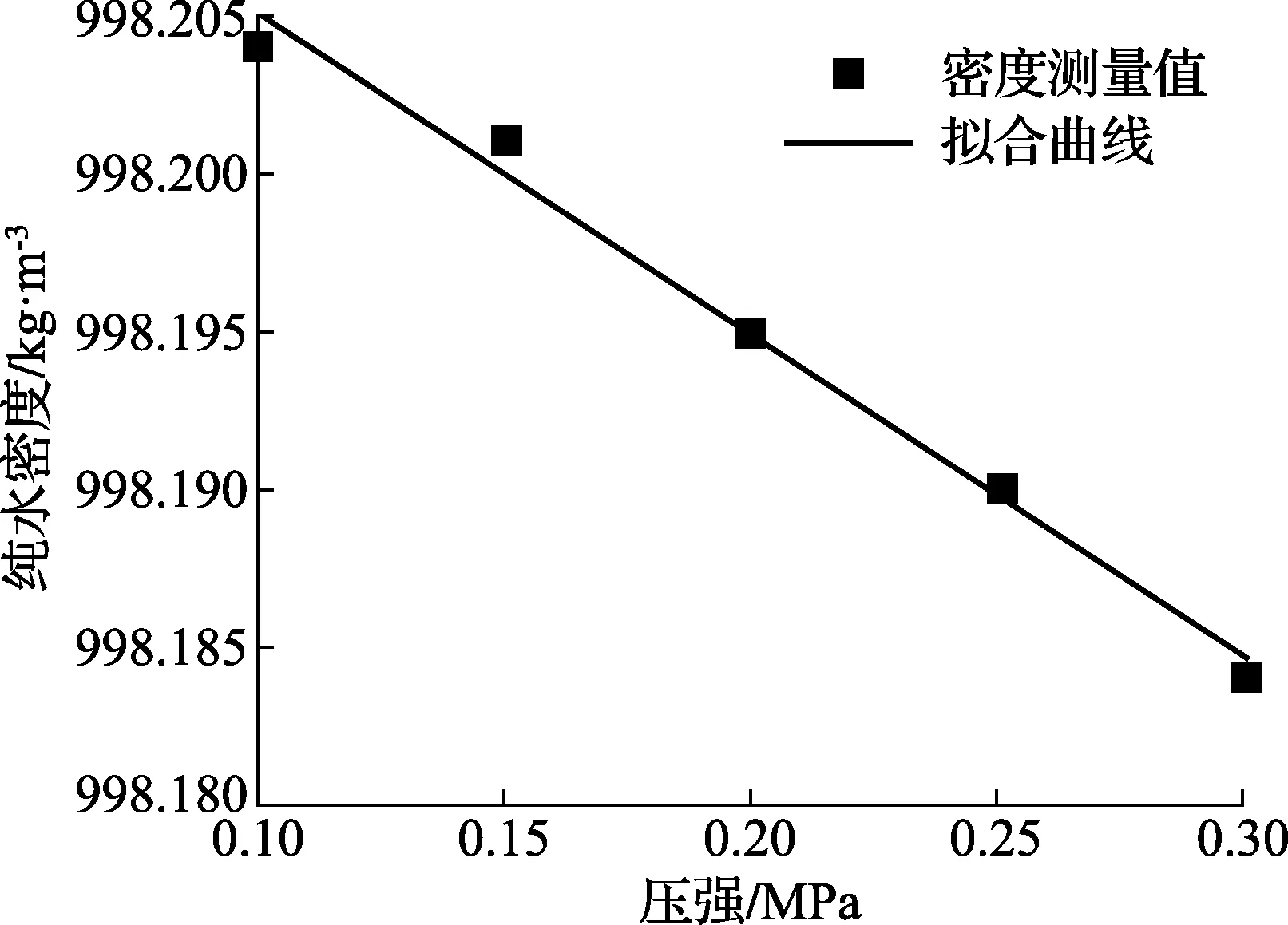
图2 测量水在20 ℃时加压的显示密度值

由图2可知,发现显示的密度值随着压强增大而减小,这显然与一般规律不符。原因正是振动管的参数发生了不可忽略的变化,这导致光学传感器测得的振荡值τ与液体密度的关系发生了改变。因此,在施加额外压强时,为了准确得到密度值,需要对振动管密度计参数A和B进行校准。

2.2 谐振法校准原理

A与振动管的振动常数K和体积V有关,B与振动管的质量m和体积V相关:

(2)

(3)

由式(2)和式(3)可知,压强变大后,振动管的体积V和振动常数K都变大,这导致A和B发生变化。为了校准压强对A和B的影响,将这2个参数均视为压强的相关函数。

考虑到纯水和空气的密度与压强之间的关系研究已经十分成熟,使用纯水和空气来校准压强对振动管密度计的影响。在某个温度点,给振动管密度计施加一定的压强,由该温度点各个压强下水的密度ρw和空气的密度ρa可以计算出各个压强值对应的A和B。由式(1)可以得到参数A和B的计算公式:

(4)

(5)

空气和水的振荡值τa和τw均由密度值内置光学传感器测得。空气的密度值ρa由CIMP-2007推荐的空气密度计算公式直接算得[11,12]。而水的密度ρw由CIPM推荐的常压下0 ～40 ℃范围的公式计算[13,14],再经过压强系数k校准得到:

(6)

k=1+(k0+k1t+k2t)Δp

(7)

式中:t为温度;Δp为压强变化量;系数a1～a5均为常数,a1=-3.983 04±0.000 67 ℃-1,a2=301.797 ℃-1,a3=522 528.9 ℃-1,a4=69.348 81 ℃-1,a5=999.974 95±0.000 84 kg/m3;压强系数k0～k2均为常数,k0=50.74×10-11Pa-1,k1=-0.326×10-11Pa-1,k2=0.004 16×10-11Pa-1。

通过式(4)与式(5)计算得到各个压强值下的A和B,在低压情况下A和B与压强Δp呈线性关系:

A(Δp)=A0(1+cAΔp)

(8)

B(Δp)=B0(1+cBΔp)

(9)

式中:A0和B0分别为未施加压强时的参数;cA和cB为压强系数。经过校准,得到不同温度点下参数A和B与压强Δp的关系,由振荡值τ便可以得到不同压强下液体的密度值。将式(8)和式(9)代入式(1)可得:

ρ(τ,Δp)=A0(1+cAΔp)τ2-B0(1+cBΔp)

(10)

再由不同压强下的液体密度值和对应的压强值计算出液体的压缩系数ε:

ρ(t,Δp)=ρ(t,p0)(1+εΔp)

(11)

式中p0为参考压强(101.325 kPa)。

通过上述推导,由压强系数cA和cB计算得到校准密度ρ(τ,Δp),从而由式(11)建立了压强和校准密度之间的关系。

3 实验与分析

在测量压缩系数之前,使用密度值可溯源到国际标准的纯水和空气来校准振动管密度计,拟合得到密度计参数与压强的关系函数。由测量的液体的密度值和对应的压强计算出密度标准液体的压缩系数,并与文献[15～17]结果进行对比。

3.1 实验准备

参考CIPM关键比对CCM.D-K2提供的密度标准液体,采用纯水、正十二烷、正十五烷和四氯乙烯作为密度标准液体。密度标准液体的密度通过静力称重装置由固体基准量值传递而得,其测量不确定度可以小于0.005 kg·m-3。使用的纯水经过反渗透和蒸馏得到[18,19]。纯水的密度值可溯源到国际基准,密度不需要修正,所以只需测量正十二烷、正十五烷和四氯乙烯的压缩系数。作为密度标准液体,正十二烷、正十五烷纯度均为99%,四氯乙烯纯度为98%。

采用的主要设备是振动管密度计DMA 5000M和精密压强控制器PPC 4。振动管密度计在常压下测量液体密度,显示的密度值的分辨力可达1×10-3kg/m3,准确度为5×10-3kg/m3,内部温度测量标准不确定度为0.001 ℃。压强控制器PPC4的压强相对测量不确定度为0.01%。分别在温度为20,25,30,35和40 ℃的条件下,向振动管施加的压强Δp为0.05,0.10,0.15,0.20,0.25和0.30 MPa,测量密度标准液体低压条件下的压缩系数。测量空气的压力计不确定度为5 Pa,温度计不确定度为0.1 ℃,湿度计不确定度为1%。参数A和B的测量结果如图3所示,压强系数cA和cB均由线性拟合求得,为cA=1.67×10-10Pa-1和cB=-2.30×10-10Pa-1。回归系数分别为0.997和0.998。

图3 参数A、B与压强Δp的关系

3.2 压缩系数测量

由测量结果知,在低压条件下密度和压强的关系是线性的,回归系数可达0.998,即压缩系数是定值。3种密度标准液体在5个温度点的压缩系数计算结果如表1所示。

测量过程中,不确定度主要来源于压强、振动频率、液体温度和空气温度湿度测量等因素。振动频率测量不确定度为2×10-7,施加压强相对不确定度为1×10-4,密度计单次测量液体温度不确定度为0.001℃。空气密度的不确定度为2×10-6g/cm3[11],纯水的密度的不确定度为 4×10-6g/cm3[14]。经过计算,3种液体在5个温度点下的压缩系数相对测量不确定度大约都为2%。

表1 低压下密度标准液体的压缩系数

3.3 结果分析

由表1可以看到,3种液体的压缩系数大约为 1×10-9Pa-1,所以每施加1 kPa压强,液体密度值大约会产生1×10-6的相对变化量。海拔每增加100 m,大气压强大约减小1.1 kPa,同时空气的温度和湿度也影响大气压强值,因此地域的差异对密度值的影响不可忽略。考虑到密度标准液的相对测量不确定度为6×10-6,地域压强的不同带来的密度变化就很有必要进行修正。而压缩系数可以消除这种影响,对密度基准的量值传递意义重大。

关于有机液体压缩系数的数据很少,有关压缩系数测量的文献大多是针对混合有机液体,而且大多是高压条件下的测量。与在低压下烷类压缩系数的测量文献进行数据对比,对比其中相同液体的相同温度点的值,如表2所示。

表2 压缩系数测量值和文献参考值的对比

文献[15～18]使用毛细玻璃管和气压计测量体积变化量,计算各类烷类和苯在低压条件下的压缩系数,使用的正十二烷和正十五烷试剂来源于Fluke公司,纯度为99%,压强范围为0～2 MPa,压缩系数相对不确定度低于5%。如表2所示,所测正十二烷和正十五烷的压缩系数与文献结果基本吻合,验证了基于振动管密度计测量压缩系数的有效性。

4 结 论

液体密度基准在密度量值传递中有重大意义,密度标准液体的相对测量不确定度要求到达6×10-6。为研究和修正压强对液体密度值的影响,基于U型振动管密度计工作原理,测量了在低压条件下密度标准液体压缩系数。测得在低压条件下,3种密度标准液体在20 ℃,25 ℃,30 ℃,35 ℃和40 ℃等5个温度点的压缩系数值,并通过对比相关文献数据,验证了该方法的有效性。测量结果的相对不确定度为2%。经过分析测量结果,每100 m的海拔差距引起的液体密度相对变化量大约为1×10-6,故海拔对液体密度基准的影响不可忽略,密度标准液的压缩系数对校准密度值有重要意义。

[参考文献]

[1] Fujii K. Present state of the solid and liquid density standards [J].Metrologia, 2004, 41:S1-S15.

[2] Fujii K. Precision density measurements of solid materials by hydrostatic weighing [J].MeasurementScience&Technology, 2006, 17(10):2 551-2 559.

[3] Bettin H, Toth H. Solid density determination by the pressure-of-flotation method [J].MeasurementScience&Technology, 2006, 17(10):2 567-2 573.

[4] Fehlauer H, Wolf H. Density reference liquids certified by the Physikalisch-Technische Bundesanstalt [J].MeasurementScience&Technology, 2006, 17(10):2 588-2 592.

[5] 罗志勇, 杨丽峰, 陈允昌. 基于多光束干涉原理的相移算法研究[J]. 物理学报, 2005, 54(7): 3 051-3 057.

[6] 罗志勇. 单晶硅球密度的绝对测量[J]. 计量学报, 2012, 33(5):428-431.

[7] 王金涛, 刘子勇. 基于静力悬浮原理的单晶硅球间微量密度差异精密测量方法研究[J]. 物理学报, 2013, 62(3): 374-381.

[8] WANG J T, LIU Z Y, XU C H,etal. Measurement method of compressibility and thermal expansion coefficients for density standard liquid at 2329 kg/m3based on hydrostatic suspension principle [J].ChineseJournalofMechanicalEngineering, 2014, 27(4):779-784.

[9] 崔英伟, 孙坤, 刘振兴. 油液体积弹性模量的测量[J]. 液压气动与密封, 2012, 32(3):17-19.

[10] Pena M D, Tardajos G. Isothermal compressibilities of n-alkanes and benzene [J].JournalofChemicalThermodynamics, 1978, 10(1): 19-24.

[11] Picard A, Davis R S, Gläser M,etal. Revised formula for the density of moist air (CIPM-2007)[J].Metrologia, 2008, 45(2):149-155.

[12] Sanmamed Y A, Dopazo-Paz A, González-Salgado D,etal. An accurate calibration method for high pressure vibrating tube densimeters in the density interval (700 to 1600) kg· m3[J].JournalofChemicalThermodynamics, 2009, 41(9):1 060-1 068.

[13] YIN J, WU J, MENG X,etal. Compressed liquid density measurements of dimethyl ether with a vibrating tube densimeter [J].JournalofChemicalThermodynamics. 2011, 43(9):1 371-1 374.

[14] Tanaka M, Girard G, Davis R,etal. Recommended table for the density of water between 0 °C and 40 °C based on recent experimental reports[J]. Metrologia, 2001, 38(4):301-309.

[15] 文晓林, 何家骏. 二组分系统的压缩系数和热压力系数[J]. 物理化学学报, 1992, 8(6): 804-808.

[16] 李之昊, 王金涛, 刘翔, 等. 基于Karl Fischer电位滴定原理的超微量液体容积精密测量方法[J]. 计量学报, 2017, 38(3): 296-299.

[17] Aicart E, Tardajos G, Pea M D. Isothermal compressibility of cyclohexane +n-tridecane and +n-pentadecane at 298.15, 308.15, 318.15, and 333.15 K[J].JournalofChemicalThermodynamics, 1981, 13(8):783-788.

[18] Fehlauer H, Wolf H. Density reference liquids certified by the Physikalisch-Technische Bundesanstalt[J].MeasurementScience&Technology, 2006, 17(10):2 588-2 592.