基于指数应变能密度的弦支穹顶结构失效准则研究

张 明, 田始轩, 刘占辉, 周广春, 陈志伟(. 西南交通大学 土木工程学院, 成都 6003; . 奥雅纳工程咨询(上海)有限公司北京分公司, 北京 0000;3. 结构工程灾变与控制教育部生点实验室(哈尔滨工业大学), 哈尔滨 50090;4. 哈尔滨工业大学 土木工程学院, 哈尔滨 50090)

日本学者川口卫于1993年在对索穹顶和单层网壳两种结构体系进行充分研究的基础上，立足于张拉整体的概念，将索穹顶结构构造模式应用于单层网壳，提出了弦支穹顶结构体系。因此，弦支穹顶结构是基于单层网壳穹顶和弦支体系构建而成的一种新型空间预应力自平衡体系。与单层网壳和索穹顶等结构相比，弦支穹顶结构具有自重轻、跨度大、受力合理且对支座水平推力接近于零等众多优点。与此同时，该类结构具有更强的抗震性能，历次地震及振动台实验均表明此类结构非常适合作为震区的避难场所。国内外科研人员在弦支穹顶结构体系的结构构造、静力和动力力性能等方面均进行了深入分析，在理论和工程应用方面取得了具有学术意义和实用价值的研究成果[1-8]。但对弦支穹顶结构体系在地震，特别是强震作用下的失效机理和失效模式等问题的研究，仍处于初步探索阶段。截至目前，还没有一套较为合理的判断弦支穹顶结构体系失效荷载和模式的失效准则，这严重制约该类结构体系朝着自重更轻、跨度更大、性态设计及绿色等方向发展。

基于能量的研究是公认的能够较好地反映结构在地震、特别是强震作用下的真实响应及弹塑性性能的方法。能量分析方法涉及力和变形、或者应力和应变的共同表现，且其理论基础既严密又普适。从20世纪50年代始，许多学者应用能量分析方法对不同结构进行了抗震分析、并给出了基于变形能的结构破坏准则和设计公式[9-19]。目前，国内学者从能量的角度已经对高次超静定的大跨度空间结构进行一定的分析研究。何艳丽等[20]考虑了不同模态对整个结构在脉动风作用下应变能的贡献多少来定义模态对结构风振响应的贡献，并对截断模态之后的模态的能量进行补偿，提出了一种简单、有效的方法来补偿由于高阶模态截断而产生的误差。杜文风等[21]针对地震作用下单层球面网壳结构的动力强度破坏问题，将结构塑性累积耗能与最大变形进行线性组合建立了动力强度破坏的双控准则，并应用动力破坏指数判定结构的动力破坏程度。刘英亮等[22]通过ANSYS软件二次开发，编制了相应的前后处理程序，实现了网壳结构的能量分析；并以K8型单层球面网壳为例，在对其进行全荷载域动力时程分析的基础上，归纳和总结了单层球面网壳结构在强震作用下能量响应规律。

上述学者基于能量的方法对大跨度空间结构的动力性能进行了深入地研究，杜文凤等还将结构失效时刻的塑性累积耗能与最大变形进行组合，建立了基于变形和能量的损伤模型，对单层球面网壳的动力强度破坏进行判断。从工程应用的角度来讲，这些研究成果对单层网壳的抗震设计与建造具有重大作用。在此基础上，需要进一步开展规律性研究，探索弦支穹顶结构的失效机理，建立动力失效判断准则对弦支穹顶结构失效模式和失效荷载进行预测。本文从结构细部应变能密度出发，针对强震作用下弦支穹顶结构失效机理和失效模式问题，建立精细化有限元模型，对不同类型的弦支穹顶结构在地震作用下进行了全荷载域动力时程分析。通过对结构不同动力响应特征(如节点动位移、单元动能、应变、应变能和屈服杆件比例等)的统计和再建模分析、探索了地震作用下弦支穹顶结构的响应规律。进而，初步建立了基于指数应变能密度的该类结构动力失效判断准则。

1 结构指数应变能密度及特性

应变能是指在外力作用下结构变形时内部所储存的能量，包括弹性应变能和塑性应变能。参照文献[23]，能够体现结构整体受力特征的Id计算式为

(1)

式中：Id是结构整体的指数应变能密度和值;N是结构的全部单元数目；Ii是动力时程响应分析中最后一荷载子步处结构的第i个单元的应变能密度，其计算公式为

(2)

式中：(σij)e和(εij)e为第i个单元第j个积分点的弹性应力和应变；(σij)p和(εij)p为第i个单元第j个积分点的塑性应力和应变；n为单元i的积分点数目。

当单元所承受的外荷载较小时，可忽略单元的变形和位移等几何非线性的影响，而仅考虑材料非线性问题，其应变和应力可近似按下式计算[24]

εij=BK-1F

(3)

σij=Cεij

(4)

式中：B，K和C分别是单元的应变-位移矩阵，刚度矩阵及材料的应力-应变关系矩阵，小变形时均近似为常量；F为单元外力。

当单元的内力较大，考虑结构几何非线性时，单元的应变和应力按Green-Lagrange应变和真实应力计算[25]

(6)

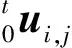
分析式(3)和(4)可知，当动荷载峰值A较小时(即F较小)，单元应变和应力均与外荷载成线性关系，进而单元的应变能密度Ii与加速度峰值的关系近似为二次曲线关系。随着A值的持续增加，单元的变形将逐渐增大，几何非线性对单元的应变和应力的影响将不可忽略。由式(5)和(6)可知，考虑几何非线性的影响后，单元的应变和应力不再仅与外荷载保持定量的线性关系，还与单元的刚体位移、转动和大变形等有定量的关系。出现较大几何变形后，单元的应变和应力将呈现较大增加。经反复试算发现，当单元外荷载达到某个量级后，大多数单元的几何变形会急骤增加。从而引起式(2)中单元的应变能密度Ii急剧增加。从结构受力状态概念上判断，产生了较大几何变形的单元将失去了继续承载的能力。对于弦支穹顶结构而言，因为其超静定次数较高，部分单元的失效难以致使结构失去稳定承载的能力，而应是一定数量结构单元的失效才能发展成结构整体的失效。因此当结构失效时，将有一定数量的单元产生较大几何非线性变形，即有一定数量单元的应变能密度Ii急骤增加，进而造成结构整体的应变能密度急骤增加。此时，对应于Ii-A曲线将出现突变(如图1所示)。

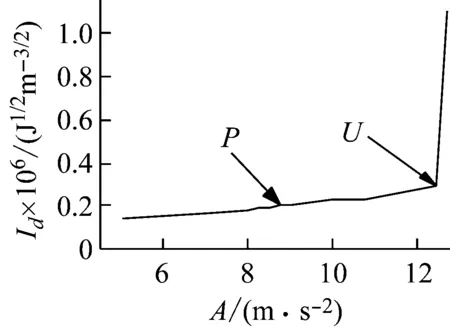
图1 Q4010121806b的Id-A的变化曲线Fig.1 The relationship between Id and A of suspend- dome Q4010121806b

图1给出了频率为5 Hz简谐波作用弦支穹结构Q4010121806b的Id-A的变化曲线。从图中可见P点之前为直线段，表示该弦支穹顶结构处于弹性工作状态。当网壳部分单元进入塑性时，该部分单元的弹性模量将发生变化，进而造成单元刚度发生变化，所以此时Id不再是A的严格一次函数，而是如图1中P点到U点之间所示的弱非线性关系，此时结构处于弹塑性工作状态。此阶段，虽然部分单元进入了塑性工作状态，但相对于结构整体的弹性应变能密度而言，塑性应变能密度体量并不是很大，还不至于影响结构的正常工作状态；可当结构整体塑性应变能密度比较大，即整体塑性发展比较深、几何非线性影响较大时，有可能失去稳定的工作性能(表现为图1中U点之后Id-A曲线的突变)，即已达到极限状态。

为了验证这一理论并进一步给出弦支穹顶结构的失效判断准则，下文将对典型弦支穹顶结构进行全荷载域动力时程分析，并在此基础上，分析其Id-A关系曲线的变化规律。

2 弦支穹顶结构有限元模拟简介

本文基于Ansys有限元软件对典型弦支穹顶结构(如图2所示)进行全荷载域动力时程分析。以跨度为40 m的K6型弦支穹顶结构为例，结构模型的杆件和拉索均采用双线性随动强化本构关系模型，Et=0.02E，采用 Rayleigh阻尼，阻尼比为0.02。计算过程中，关闭重力加速度，仅考虑地震动对结构的动力响应。矢跨比为1/7，撑杆高度由内到外的比例为1∶1.5，内三环为2.0 m，外两环为3.0 m。环向索的预拉力由内到外分别设置为5 kN、10 kN、20 kN、50 kN、100 kN；通过找形分析，预拉力以初应变的形式施加在索单元的实常数中。模型上部网壳的钢管截面为150 mm×6.0 mm，材料为Q345钢，采用PIPE20单元模拟。下部撑杆截面面积为686.88 mm2，材料同样为Q345钢，采用LINK8单元模拟。径向拉索和环向索由内向外分别编号，单元材料为半平行钢丝束，屈服强度为1 330 MPa，采用LINK10单元模拟。

(a)弦支穹顶结构俯视图(b)弦支穹顶结构侧面图

图2 弦支穹顶结构模型示意图

Fig.2 The suspen-dome model

本文选用的40 m、60 m跨度弦支穹顶结构索材的截面面积见表1。杆件的弹性模量为206 GPa，索材的弹性模量为180 GPa。屋面荷载为1 000 N/m2，等效为节点集中质量，采用MASS21单元模拟。另外，撑杆的类型及高度见表2。为了方便表述，本文对不同类型的弦支穹顶结构进行统一编号，如图3所示。

对所选类型的弦支穹顶结构基于ANSYS有限元软件进行全荷载域动力时程响应分析，并实时提取各级动荷载幅值作用下弦支穹顶结构全部节点的动位移、全部单元的应变能及相应的应变能密度，其中三向简谐波及TAFT地震波作用下全部单元的应变能密度和值计算结果见表3。限于篇幅，表3中仅列出了部分加速度峰值作用下全部单元的应变能密度和值。

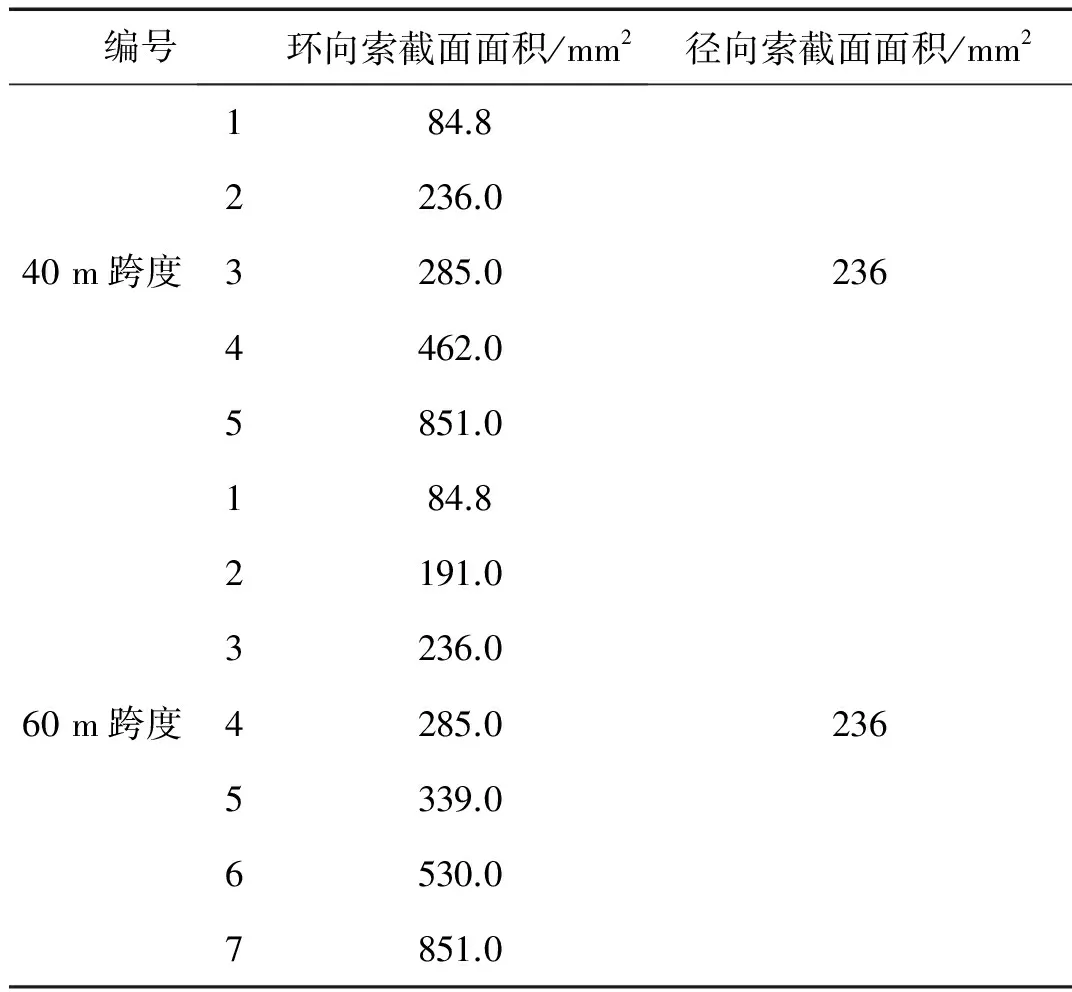
表1 索材的材料表Tab.1 Characteristic of cable

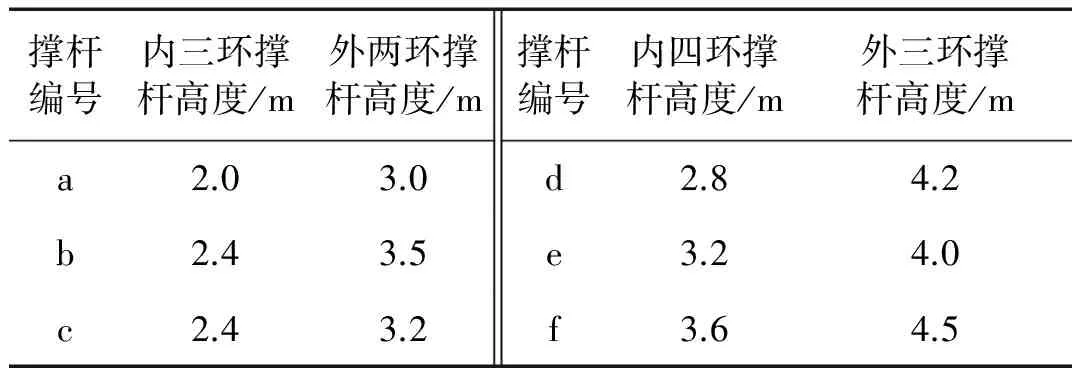
表2 撑杆类型及高度Tab.2 Strut types and height

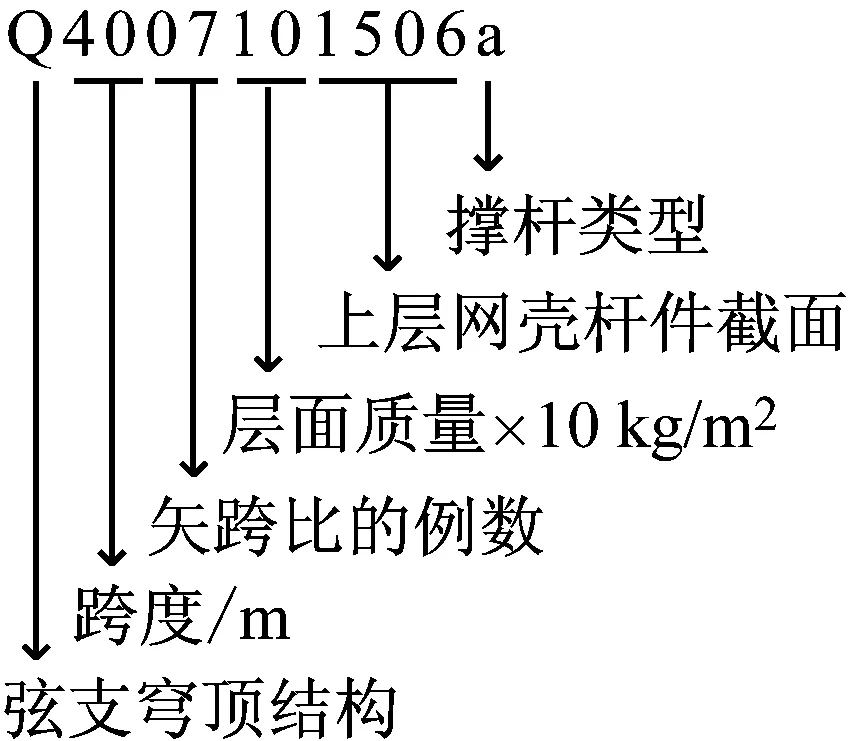
图3 弦支穹顶结构模型编号说明图Fig.3 The serial number and declaration of suspen-dome model

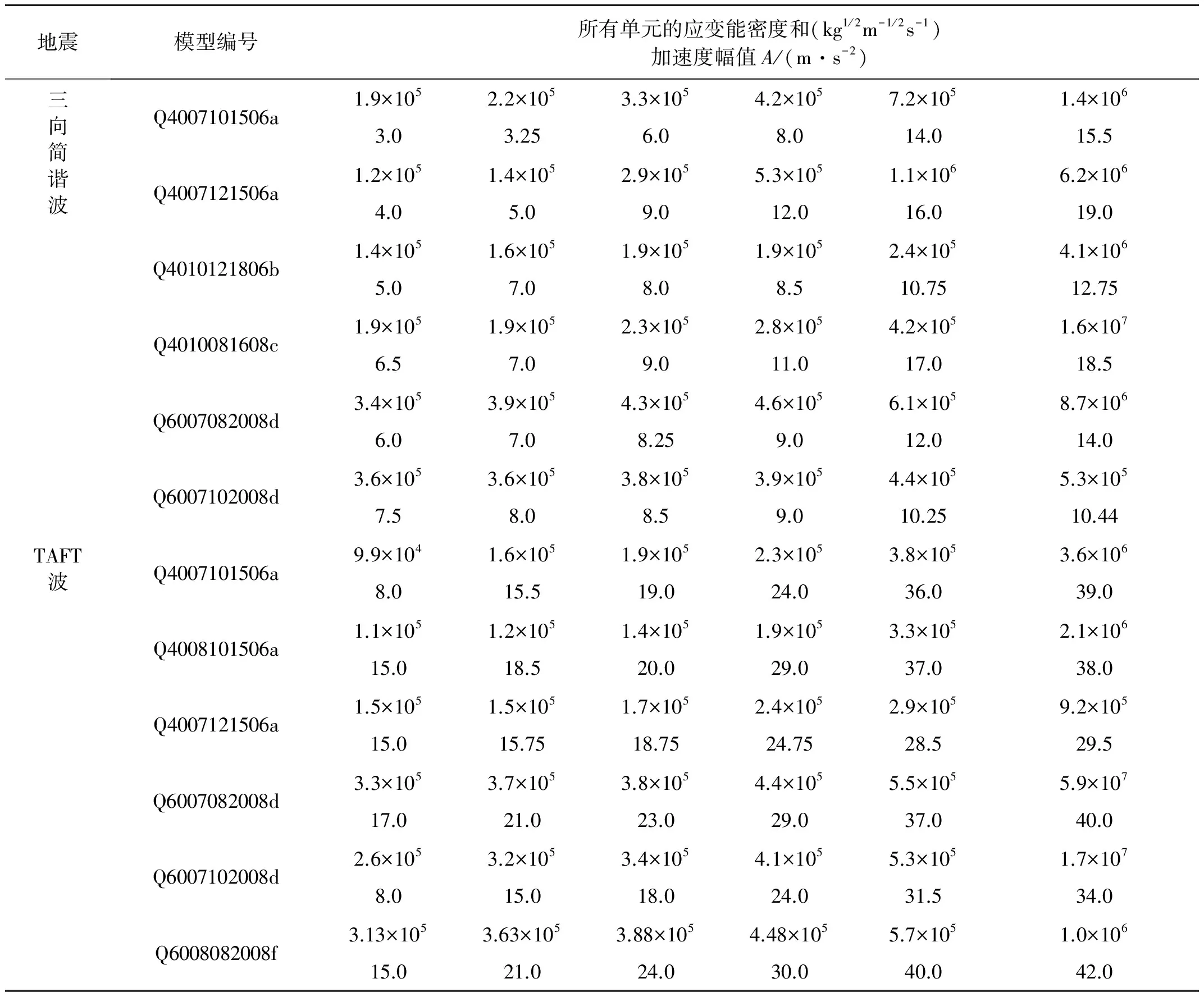
表3 弦支穹顶结构应变能密度及加速度幅值统计Tab.3 Statistics of the sum of strain energy density corresponding to their acceleration amplitudes for selected suspen-domes

3 Id-A关系曲线分析

基于全荷载域动力时程分析结果，分别绘制弦支穹顶结构在三向简谐波与TAFT波作用下，指数应变能密度和值Id与加速度幅值A的关系曲线如图4和图5所示。这些图中均存在着三个工作状态，即弹性工作状态、弹塑性工作状态和失效状态(没有在图中给出P点和U点)。在结构的弹性工作阶段，Id与A同样均呈线性关系；在结构进入弹塑性工作阶段后，虽部分杆件的弹性模量转变为割线模量，但结构塑性发展程度较浅，Id与A仍能保持近似线性增长的趋势，随着更多单元进入塑性，结构的刚度和强度不断退化，Id与A逐渐呈非线性变化。当A增加到某一值后，结构整体指数应变密度和值Id同样会突然增大。此后，结构虽然能继续承载，但已经失去了保持稳定工作状态的能力，此时可以认为结构已经达到了承载能力极限状态。从结构受力状态的角度来判断，Id-A关系曲线能够较合理地判断结构的失效模式及失效荷载。

Q4007101506aQ4007121506a

Q4010121806bQ4010081608c

Q6007082008dQ6007102008d

图4 三向简谐波作用下Id与加速度幅值(A)关系曲线

Fig.4 The relationship betweenIdandAunder harmonic earthquake waves with three-dimension

4 指数应变能密度失效状态判断准则

基于第1部分定性的理论推导和第3部分Id-A关系曲线分析，本文给出了判定弦支穹顶结构的失效状态的结构指数应变能密度破坏系数ki，表达式为

Q4007101506aQ4008101506a

Q4007121506aQ6007082008d

Q6007102008dQ6008082008f

图5 TAFT波作用下Id与加速度幅值(A)关系曲线

Fig.5 The relationship betweenIdandAunder TAFT earthquake waves

ki≥1

(7)

式中：ki=[(Ii-I1)×Amax]/[(Ai-A1) ×Imax]；Ai为第i步的加速度峰值；Ii是对应于加速度峰值为Ai时的结构整体指数应变能密度和值。

式(7)可以对Id-A曲线的斜率变化进行度量，经统计发现结构处于工作状态时，ki位于0～1之间；但当结构失效时，ki均大于1。另外，当Id-A曲线一直缓慢发展时，难以区分结构的工作状态和失效状态，此时可以依据式(7)对结构的工作状态和失效荷载进行判断。

基于式(7)，分别计算出所选弦支穹顶结构在三向简谐波和TAFT波作用下的结构指数应变能密度破坏系数与加速度幅值的关系曲线，如图6和7所示。

参考式(4)，由图6和7可以定量地判断出弦支穹顶结构的失效状态位置及其失效荷载。地震作用下，不同类型的弦支穹顶结构在达到失效状态之前，结构指数应变能密度破坏系数保持稳定增长；失效后，该值均大于等于1。因此，可以基于该参数来判断弦支穹顶结构的失效状态及失效荷载。

5 指数应变能密度失效准则的合理性讨论

为了验证指数应变能密度失效判断准则的合理性，表4和5分别列出了所选弦支穹顶结构在简谐波和TAFT地震波作用下结构的失效荷载及相应的动力响应特征。

Q4007101506aQ4007121506a

Q4010121806bQ4010081606e

Q6007082008dQ6007102008d

图6 简谐波作用下结构破坏系数k与加速度幅值A关系曲线

Fig.6 The relationship between structure damage coefficientkandAunder harmonic earthquake waves with three-dimension

Q4007101506aQ4008101506a

Q4007121506aQ6007102008d

Q6007082008dQ6008082008f

图7 TAFT波作用下结构破坏系数k与加速度幅值A关系曲线

Fig.7 The relationship between structure damage coefficientkandAunder TAFT earthquake waves

从表4和5中可以看出结构的失效荷载均大于弹塑性分界点所对应的加速度峰值，表明所选弦支穹顶结构均进入了弹塑性工作状态；失效荷载与弹塑性分界点所对应的加速度峰之差均较大，表明弦支穹顶结构有良好的弹塑性工作能力；最大节点位移与结构跨度的比值在2.9/400～1.1/600范围内，平均值为1/250，满足《空间网格结构技术规程》[26]中关于空间网格结构的容许挠度值的限值。屈服杆件比例范围为0.17%～14.03%，均值为5.42%，表明该类型结构体系失效时塑性变形有一定程度的发展，但塑性变形发展深度并不是很大，基本符合《钢结构设计规范》[27]中允许利用杆件截面一定塑性的规定。同时，较少的屈服杆件比例，表明这类结构体系的失效模式更接近动力失稳，这与单层球面网壳强震作用下失效时塑性发展较深不同，后者更接近动力强度破坏。

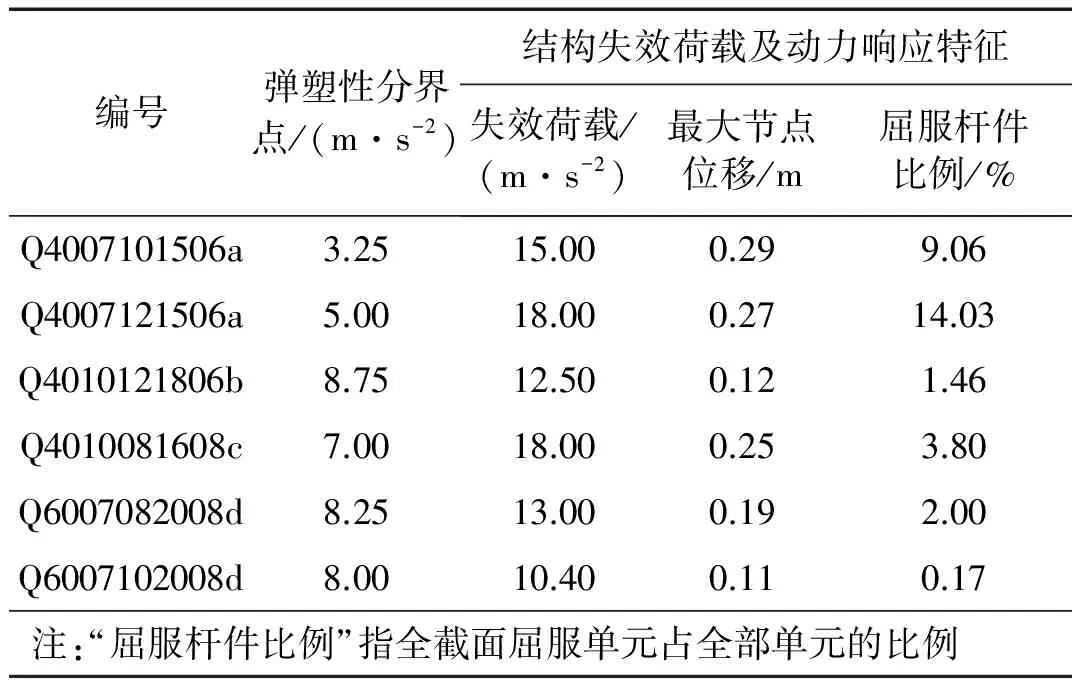
表4 简谐波作用下结构失效特征统计Tab.4 The failure characteristics of suspen-domes subjectedto harmonic earthquake waves with three-dimension

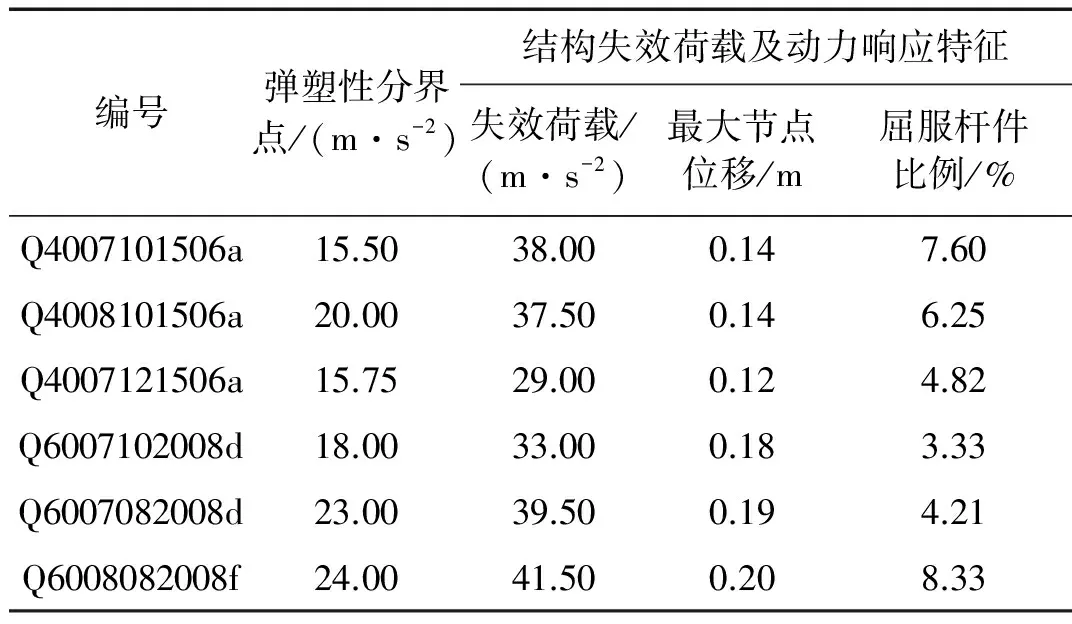
表5 TAFT波作用下结构失效特征统计Tab.5 The failure characteristics of suspen-domes

综上所述，本文所提出的“基于指数应变能密度失效判断准则”能够较为合理地界定弦支穹顶结构失效模式及失效荷载。同时，也能够分析出弦支穹顶结构体系在地震作用下具有良好的动力工作性能。

6 结 论

基于定性的理论推导和通过对强震作用下弦支穹顶结构应变能密度的分析，本文初步揭示了结构指数应变能密度随地震动强度的变化规律，并据此给出了预测弦支穹顶结构失效荷载的判定指标，结论如下：

(1) 弦支穹顶结构的受力状态包括弹性工作状态、弹塑性工作状态和失效状态三个工作状态。弹性工作状态，结构指数应变能密度和值Id与地震动强度A呈线性关系；弹塑性工作状态，结构指数应变能密度和值Id与地震动强度A呈弱非线性关系；当地震动强度A达到一定值时，Id-A曲线发生突变，此后Id-A曲线非常不稳定，表征结构失效。因此，从结构指数应变能密度和值和加速度峰值关系的角度来看，结构失效表现为动力失稳。与此同时，弦支穹顶结构失效时刻较少的屈服杆件比例，也进一步表明该类结构更易发生动力失稳破坏。

(2) 基于Id-A曲线上的拐点U，本文初步给出了弦支穹顶结构动力失效荷载的判断指标。

(3) 由于弦支穹顶结构的构造不同，结构的受力状态会有区别，因此本文拓展了文献[23]中Id-A曲线的适用范围，基于指数应变能密度对结构整体受力状态下分析方法做了进一步发展。

(4) 本文是基于有限元模拟分析得到的数据，对弦支穹顶结构在地震作用下的受力状态进行的分析，故本研究的不足之处在于缺少实验验证。接下来工作中，将着手于实验分析等相关研究。

(5) 结构整体失效与局部单元失效的数量及其分布有直接关系，但是定量地分析这一问题，还需要作者及其团队成员进一步展开研究。

致谢感谢西南交通大学和哈尔滨工业大学“空间结构研究中心”为本课题研究所提供的技术支持！

参 考 文 献

[1] KAWAGUCHI M, ABE M, HATATO T, et al. Structural tests on the suspen-dome system[C]∥The IASS-ASCE International Symposium 1994. Atlanta, GA, 1994: 383-392.

[2] KAWAGUCHI M, ABE M, TATEMICHI I. Design, tests and realization of suspen-dome system[J]. Journal of the International Association for Shell and Spatial Structures, 1999, 40(3): 179-192.

[3] 陈志华. 弦支穹顶结构体系及其结构特性分析[J]. 建筑结构, 2004, 34(5): 38-41.

CHEN Zhihua. Suspendome structure system and characteristic analysis[J]. Building Structure, 2004, 34(5): 38-41.

[4] 陈志华, 郭云, 李阳. 弦支穹顶结构预应力及动力性能理论与实验研究[J]. 建筑结构, 2004, 34(5): 42-45.

CHEN Zhihua, GUO Yun, LI Yang. Experimental research and analysis of the prestress and dynamic behavior for suspendome structure system[J]. Building Structure, 2004, 34(5): 42-45.

[5] 陈志华, 李阳, 康文江. 联方型弦支穹顶研究[J]. 土木工程学报, 2005, 38(5): 34-40.

CHEN Zhihua, LI Yang, KANG Wenjiang. Analysis of lamella suspendome systems[J]. China Civil Engineering Journal, 2005, 38(5): 34-40.

[6] 钱曙珊. 大跨弦支穹顶结构的动力反应分析[J]. 天津大学学报(自然科学与工程技术版), 2010, 43(1): 26-31.

QIAN Shushan. Analysis of dynamic response for long span suspend-dome structure[J]. Journal of Tianjin University (Science and Technology), 2010, 43(1): 26-31.

[7] 周臻, 孟少平, 吴京. 大跨弦支穹顶结构的振动模态与地震响应分析[J]. 振动、测试与诊断, 2013, 33(4): 609-613.

ZHOU Zhen, MENG Shaoping, WU Jing. Analysis of vibration modes and seismic response for long span suspend-dome structure[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(4): 609-613.

[8] 赵均, 徐金蓓, 甘明, 等. 椭球面弦支穹顶结构的稳定性[J]. 北京工业大学学报, 2013, 39(12): 1821-1826.

ZHAO Jun, XU Jinbei, GAN Ming, et al. Stability analysis of ellipsoid suspend-dome[J]. Journal of Beijing University of Technology, 2013, 39(12): 1821-1826.

[9] HOUSNER G W. Behavior of structures during earthquake[J]. Journal of the Engineering Mechanics Division, 1959, 85(4): 109-129.

[10] AKIYAMA H. Earthquake resistant limit state design for buildings[M]. Tokyo: University of Tokyo Press, 1985.

[11] 马千里. 钢筋混凝土框架结构基于能量抗震设计方法研究[D]. 北京: 清华大学, 2009.

[12] FAJFAR P. Equivalent ductility factors taking into account low-cycle fatigue[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(9): 837-848.

[13] 欧进萍, 何政, 吴斌, 等. 钢筋混凝土结构基于地震损伤性能的设计[J]. 地震工程与工程振动, 1999, 19(1): 21-30.

OU Jinping, HE Zheng, WU Bin, et al. Seismic damage performance-based design of reinforced concrete structures[J]. Earthquake Engineering and Engineering Vibration, 1999, 19(1): 21-30.

[14] RIDDELL R, GARCIA J E. Hysteretic energy spectrum and damage control[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(12): 1791-1816.

[15] 陈永祁, 龚思礼. 结构在地震动时延性和累积塑性耗能的双重破坏准则[J]. 建筑结构学报, 1986, 7(1): 35-48.

CHEN Yongqi, GONG Sili. Double control damage index of structural ductility and dissipated energy during earthquake[J]. Journal of Building Structures, 1986, 7(1): 35-48.

[16] 陈逵，刘哲锋，沈蒲生. 结构瞬时输入能量反应持时谱的研究[J]. 工程力学, 2011(1): 19-25.

CHEN Kui, LIU Zhefeng, SHEN Pusheng. Study of the duration spectra of structural momentary input energy response[J]. Engineering Mechanics, 2011(1): 19-25.

[17] YE L P, OTANI S. Maximum seismic displacement of inelastic systems based on energy concept[J]. Earthquake Engineering & Structural Dynamics, 1999, 28(12): 1483-1499.

[18] 周云, 乐登, 邓雪松. 设计用地震动总输入能量谱研究[J]. 工程抗震与加固改造, 2008, 30(5): 1-7.

ZHOU Yun, YUE Deng, DENG Xuesong. Research on input energy spectra for design of earthquake strong motion[J]. Earthquake Resistant Engineering and Retrofitting, 2008, 30(5): 1-7.

[19] 王德才, 叶献国, 常磊. 考虑场地条件与设计地震分组的输入能量谱研究[J]. 地震学报, 2011, 33(1): 91-102.

WANG Decai, YE Xianguo, CHANG Lei. A study on input energy spectrum in consideration of site effect and design earthquake classification[J]. Acta Seismologica Sinica, 2011, 33(1): 91-102.

[20] 何艳丽, 董石麟, 龚景海. 空间网格结构频域风振响应分析模态补偿法[J].工程力学, 2002, 19(4): 1-6.

HE Yanli, DONG Shilin, GONG Jinghai. Wind-induced response of spatial structures with mode compensation in frequency domain[J]. Engineering Mechanics, 2002, 19(4): 1-6.

[21] 杜文风, 高博青, 董石麟. 弦支穹顶结构动力强度破坏的双控准则[J].浙江大学学报(工学版), 2007, 41(11): 1916-1920.

DU Wenfeng, GAO Boqing, DONG Shilin. Double-control criterion of dynamical strength failure for single layer latticed shells[J]. Journal of Zhejiang University (Engineering Science), 2007, 41(11): 1916-1920.

[22] 刘英亮, 邢佶慧. 基于能量的单层球面网壳强震响应规律研究[J]. 建筑结构学报, 2010(增刊2): 30-33.

LU Yingliang, XING Jihui. Energy-based research on response of single-layer reticulated domes subjected to severe earthquakes[J]. Journal of Building Structures, 2010(Sup2): 30-33.

[23] 张明, 张瑀, 周广春, 等. 基于应变能密度的单层球面网壳结构失效判定准则[J]. 土木工程学报, 2014, 47(4): 56-63.

ZHANG Ming, ZHANG Yu, ZHOU Guangchun, et al. Criterion for judging failure of single-layer latticed dome based on strain energy density[J]. China Civil Engineering Journal, 2014,47(4): 56-63.

[24] BATHE K J. Finite element procedures[M]. New Jersey: Prentice-Hall, Englewood Cliffs, 1996.

[25] ANDRUET R H. Special 2-D and 3-D geometrically nonlinear finite elements for analysis of adhesively bonded joints[D]. Virginia: Virginia Polytechnic Institute and State University, 1998.

[26] 空间网格结构技术规程:JGJ 7—2010[S]. 北京: 中国建筑工业出版社, 2010.

[27] 钢结构设计规范:GB 50017—2003[S]. 北京: 中国计划出版社, 2003.