空气质量数值预报优化方法研究
赵俊日 ,肖 昕*,吴 涛,李彦鹏,贾红霞 (.中国矿业大学环境与测绘学院,江苏 徐州 6;.徐州环境监测中心站,江苏 徐州 8;.江西应用技术职业学院,江西 漳州 000;.中国环境新闻工作者协会 北京 00095)
作为当前大气环境科学研究的热点与难题,大气污染物预报预警可通过各类预报方法与手段相结合,对多种大气污染物在全球尺度下的不同类型污染过程进行模拟预测研究,成为城市.及区域大气复合污染控制研究的重要手段之一[1-3].大气污染物排放源清单是模型研究和相关控制策略制定的重要基础,但排放源估算取决于许多因素,包括社会经济、能源、土地利用、环境资料等[4].但由于统计数据的滞后性和排放因子及时空分配系数等数据的不确定性,定量估算排放源及对其进行实时更新有较大的困难,有必要通过各类“反演”模型采用自下而上的方法反演污染源提高空气质量模型的模拟精度[5].徐祥德等[6]首次提出了“nudging”源同化方法,通过迭代计算的方式逐步修正污染源,改进NO2和 SO2浓度预报效果;靳璐滨等[7]利用三维变分同化(3D-var)方法对青奥会期间南京地区的 PM10、PM2.5进行了同时同化实验,结果表明同化对初始场有显著改进.
CMAQ模型作为美国环保署推荐的第3代空气质量模拟系统Models-3的核心模块[8],对污染物区域分布及其变化趋势虽具有较强的预报能力,但由于污染源时空特征十分复杂,CMAQ污染浓度预报量与实况相比存在明显偏低的“系统性”误差[9],且CMAQ模型的物理、化学机制及参数等需不断完善,因此很多学者对空气质量模型采用后处理的方式对其进行订正来减少模型误差[10].许建明等[11]提出 CMAQ-MOS动力-统计相结合的空气质量预报技术,其试验方案表明可显著降低CMAQ模型的“系统性”预报误差;尤佳红等[12]采用WRF-RTIM的MOS方法进行冬季污染预报和霾的诊断,发现在历史污染监测资料小样本条件下,RTIM 的统计预报具有较高的精度.
然而目前国内对中小尺度空气质量数值预报优化方面的研究较少,本文综合考虑排放源清单的不确定性及模式在其背景下产生的非客观性预报偏差,采用源清单修正方法、统计修正方法对其进行优化,分析修正前后预报效果的改善程度,以期为区域空气质量改善和重污染天气预报预警提供科学依据.
1 模式设置与数据
1.1 模式设置
本文采用的空气质量模式为CMAQ(v4.7.1),CMAQ为开源的高度模块化结构模型,已被广泛应用于常规空气质量预报和决策制定当中[13],CMAQ模式所需要的气象场可由中尺度数值天气预报模式 WRF(v3.6.1)提供,该模式对多种物理过程均有不同的参数化方案,可以更为真实的模拟大气空间运动[14-16].源排放处理模式SMOKE (v3.0)可以将排放清单处理成空气质量模式需要的时空分辨率数据[17],本文中 SMOKE模式主要用于徐州本地排放源清单处理,对其进行时间、空间及化学物种分配,外两层和徐州版图区域之外的剩余部分采用清华大学 MEIC[18]清单排放数据.模式采用的主要参数化方案如表1、2所示.
如图 1所示,本文中所有模式采用三层嵌套方式模拟,WRF模式和CMAQ模式采用兰伯特投影坐标系,坐标原点为117°E和45°N,两条真纬线为北纬30°和北纬60°.三层水平网格分辨率和网格数分别为 3km,9km,27km 和 97×97,94×112,76×88.第一层区域覆盖中国华北,华东及中部地区,部分东亚地区;第二层区域覆盖苏北周边的河南,山东,安徽等省份,第三层区域为目标研究区域覆盖整个徐州市.
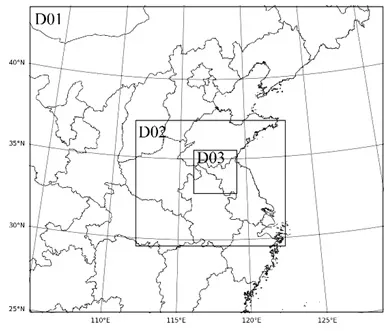
图1 研究区域Fig.1 Map of Research Regional

表1 WRF模式参数设置Table 1 Parameters setting of WRF model

表2 CMAQ模式参数设置Table 2 Parameters setting of CMAQ model
1.2 使用数据
本文使用的WRF模式输入数据源于美国国家环境预测中心发布的FNL全球再分析数据,水平分辨率为 1°×1°,地形和下垫面数据分别是USGS 30s全球地形和MODIS土地利用分类产品.徐州市本地排放源清单(基准年2015年)和大气污染物观测数据及温度、湿度、风速、风向、气压等气象观测数据由徐州环境监测中心提供.
2 研究方案设计
2.1 源清单“Nudging”修正方法
本文采用“Nudging”源同化反演方法,即在空气质量模式积分方程中构造排放源的“张弛逼近项”[19]以减少模式预报结果与实际观测浓度的误差.
假设某时刻的模拟结果误差完全是由排放源S产生,固定其他大气物理化学过程,已知实际观测污染物浓度为C*,经过n次迭代计算,模式预报的污染物浓度逐渐向实际观测值逼近,即 Cn→C*可以得到如下迭代式子:

但本研究中 CMAQ模式的第三层区域水平网格分辨率为 3km×3km,若不考虑周围面源影响,只考虑监测站点周围的点源源强,修正之后的源清单对 CMAQ模式预报结果影响甚微,所以引入反距离加权(IDW) 插值算法[20]来弥补上述缺点.
对迭代式子中设:

假设在CMAQ模式中第三层区域里有k个监测站点,各落在第(xi,yi)网格上,设其网格上的α值为αi,i=1,2,3…,k,IDW 的插值函数可描述为如下:

式中:是网格上的任意点到(xi,yi)的水平距离;p是大于0的加权幂指数
(本文中p取1.5),考虑1,2,3…,m种不同污染物,最后得到以下通式:

2.2 统计修正方法
XGBoost是在 2015年由美国华盛顿大学Chen[21]提出,XGBoost是 Gradient Boosting Machine(梯度提升机器学习算法)的C++的实现,能自动利用 CPU的多线程进行并行计算,且对算法加以改进运行速度和精度得到了很大的提升[22].
假设模型有 k个决策树,其集成模型可以如下表示:
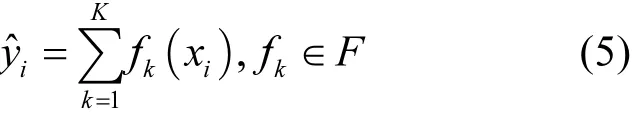
对其目标函数二阶泰勒展开得:

本文基于XGBoost算法对CMAQ模式预报的6种常规大气污染物进行统计修正.设t时间段为起报时间段,t1为5×24h,取t-t1时间段的大气污染物观测值和气象要素观测值及CMAQ模式模拟值作为训练数据,t2为 1×24h,取 t+t2时间段的WRF模式气象要素预报值及CMAQ模式预报值作为预测数据,建立统计修正回归模型,可以描述为如下方程:
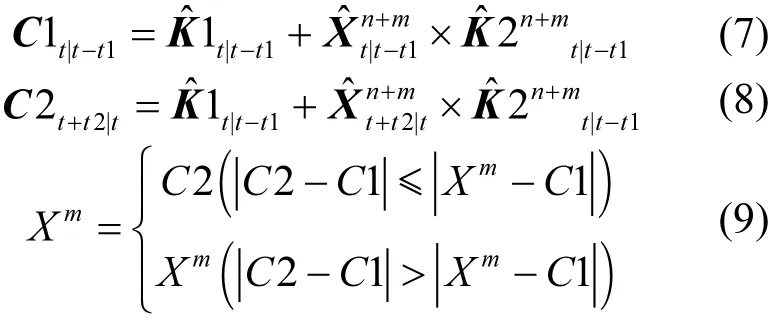
式中:为t- t1时间段的污染物浓度观测值矩阵;为t- t1时间段的n×t1维的气象要素观测值矩阵和m×t1维的CMAQ模型污染物浓度预报值矩阵;为 t+t2时间段的 n×t2维的WRF气象要素预报值矩阵和 m×t2维的 CMAQ模型污染物浓度预报值矩阵;本文中n和m分别取温度、湿度、气压、风速、风向等5列和PM2.5、PM10、O3、SO2、NO2、CO 等 6列,为t- t1时间段的(n+m)×t1维矩阵,为常数项矩阵.
3 结果与讨论
3.1 源清单“Nudging”修正结果与分析
源同化试验阶段:采用2016年12月2~6日徐州市 13个监测站点的 SO2、NO2、CO实测数据进行迭代计算.
控制试验阶段:采用初始排放源模拟 2016年12月3~31日期间徐州市区SO2、NO2、CO浓度.
预报效果检验试验:采用同化源模拟 2016年12月3~31日期间徐州市区SO2、NO2、CO浓度.
表 3给出了 2016年 12月 SO2、NO2、CO逐时浓度预报、修正值与观测值的相关系数(R)、平均绝对误差(MAE)、平均相对偏差(MFB)、平均相对误差(MFE)、均方根误差(RMSE). Boylan等[23]建议以平均相对偏差(MFB)和平均相对误差(MFE)为衡量指标评估模式预报的合理性,假如MFB值在-60%~60%之间且MEF小于75%,则可认为模式模拟结果在合理的可接受的范围内,若 MFB值在-30%~30%之间且 MEF小于50%,则可认为模式表现优秀,模拟结果在理想水平范围内.
从表3可以看出,冬季徐州市SO2、NO2逐时预报值与观测值的相关系数比较低,CO预报值与观测值的相关系数相对来说比较高,在 0.5左右,3类污染物的平均相对误差和平均相对偏差都在理想水平范围内,但平均绝对误差和均方根误差均较大.
采用初始源模拟的结果相比,修正之后 3类污染物的相关系数均有所提高,SO2、NO2的修正值与观测值的平均绝对误差和均方根误差明显减少,平均相对误差分别为 33.64%和 28.45%,平均相对偏差分别为 3.85%和-11.39%,可认为修正结果均在理想水平范围内.从修正前后的各项指标的变化幅度来看,3类污染物中 NO2修正效果最好,其次是 SO2,CO最差,其平均绝对误差和均方根误差及MFB和MFE取值范围反而变大,且相关系数提高的幅度也相对较小,优化效果不太理想,可能其模拟效果已经达到最优状态,预报效果很难进一步得到改善,下一步研究有必要对源排放、湍流扩散、化学反应、干湿沉降等过程进行分析,找出对局地 CO污染贡献最大的过程进行修正优化.

表3 2016年12月CO、SO2、NO2源清单修正误差统计表Table 3 Error statistics of simulated CO、SO2、NO2 concentration using initial and inversion emission during December 2016
图2所示为徐州市冬季2016年12月SO2、NO2、CO初始源和同化源源强空间分布,可以看出 3类污染物排放源的空间分布呈现大市区排放源强较大,其他各市区较小,冬季采暖期间燃煤及工业生产排放的污染物主要集中在市区,且冬季气象条件不利于污染物的扩散.同化源的源强大小空间分布与初始源基本相符,CO同化源的源强比初始源小,而SO2、NO2同化源的源强相对初始源高出一定比例,说明初始源清单对 CO的排放量存在一定的高估,而对SO2、NO2排放量存在一定的低估.
虽然修正之后预报效果提高了,至于清单修正之后的源强是否接近于真实排放源,与模式内部物理、化学反应参数本地化和排放源清单时间、空间、化学轮廓是否正确及使用的观测资料站点数等多种因素有关.总体而言,根据上述两种排放源的模拟结果与源强的空间分布差异一定程度上反映了冬季重污染天气过程中CO、NO2、SO2排放源强的动态分布特征.

图2 CO、NO2、SO2的初始源和同化源SMOKE处理结果空间分布(moles/s)Fig.2 CO、NO2、SO2 Spatial distributions of emission source intensity of SMOKE results第一、二行分别为初始源和同化源
3.2 统计修正结果与分析
对于初始排放源模拟的 PM2.5、PM10、O3及经“nudging”方法修正的同化源模拟的SO2、NO2、CO等6种污染物,采用基于XGBoost算法的结合 WRF预报气象要素的统计修正方法对CMAQ模型进行后处理.为了检验其修正效果,对2016年12月3~31日冬季徐州市13个监测站点逐时污染物浓度观测值、预报值及相应的修正值进行分析对比,本文取2m温度、2m相对湿度、10m风场、地面气压等5种WRF气象要素作为修正建模的训练样本,训练样本数选取参考程兴宏等[24]的方法,并考虑地区适用差异,本文采用前5d的数据作为训练样本进行滚动修正.
从表4可以看出,徐州区域SO2、NO2逐时预报值与观测值相关系数比较低,PM2.5、PM10的预报值平均绝对误差和均方根误差都比较大,而CO、O3的相关系数相对较高.经上述方法进行滚动修正之后 6种污染物预报修正值与观测值的相关系数得到了显著的提高,各项修正误差也减少了许多.对于 CO、O3修正之后其相关系数均提高了 0.15左右,经“nudging”修正之后出现的CO的MFB和MFE两项指标反而变大的现象也成功消去,平均绝对误差,均方根误差也减小了 50%左右.就相关系数而言,NO2改进幅度最大,均方根误差和平均绝对误差明显减少,平均相对误差和平均相对偏差分别为 17.24%和-2.91%,可认为修正效果非常好.PM2.5和 PM10修正值与观测值相关系数分别提高到 0.6~0.7左右,平均绝对误差和均方根误差分别减少了23.7和 23.2µg/m3,其减少幅度最大,平均相对误差和平均相对偏差均在理想水平范围内.对于SO2,修正值与观测值的相关系数提高了0.25左右,平均绝对误差和均方根误差分别减少了12.4和6.8µg/m3,平均相对误差和平均相对偏差分别为1.60%和24.37%,其修正前后各项统计指标变化幅度较明显,但相比其他 5个污染物,其预报优化效果不太理想,可能与 CMAQ模式本身对SO2模拟效果不太好有关[25],需要对模式内部物理、化学过程进行进一步的研究,找出对SO2模拟影响最大的因子进行优化.
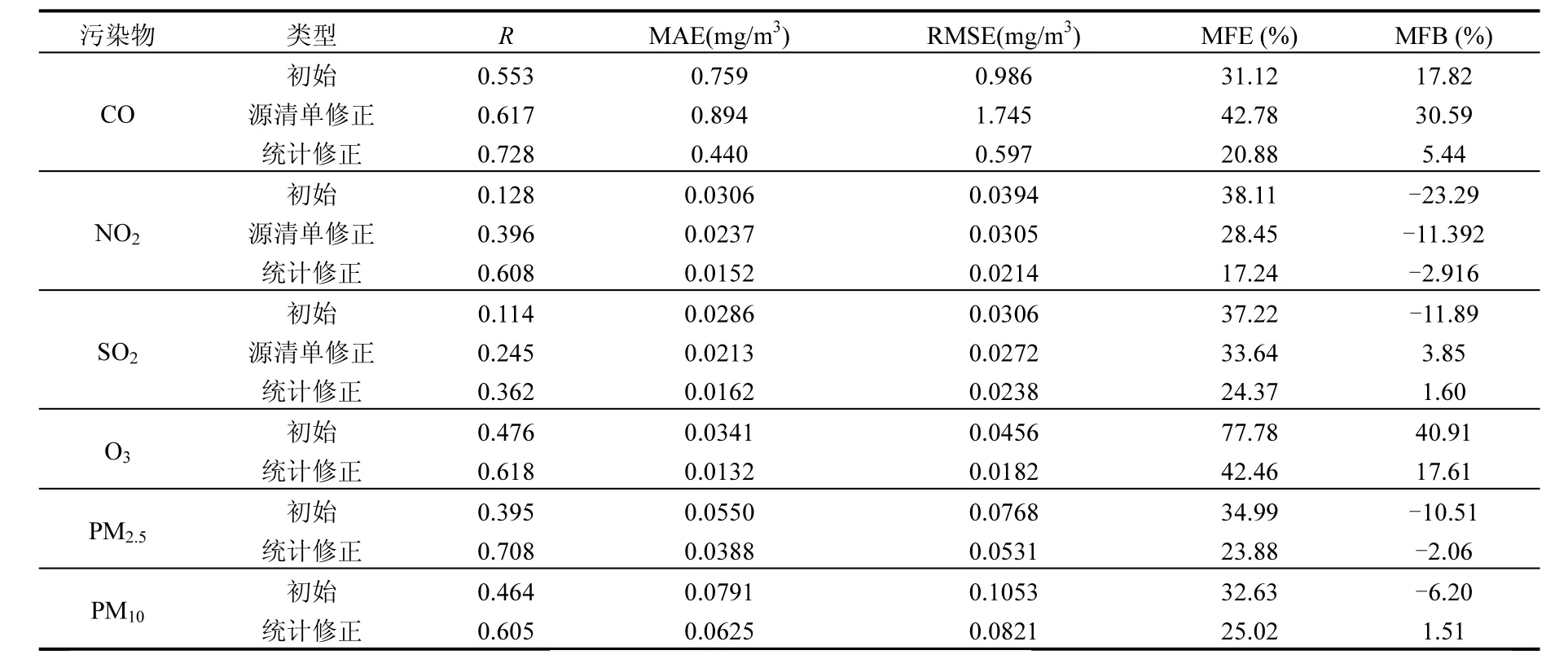
表4 2016年12月统计修正误差统计表Table 4 Error statistics of statistical revisions during December 2016
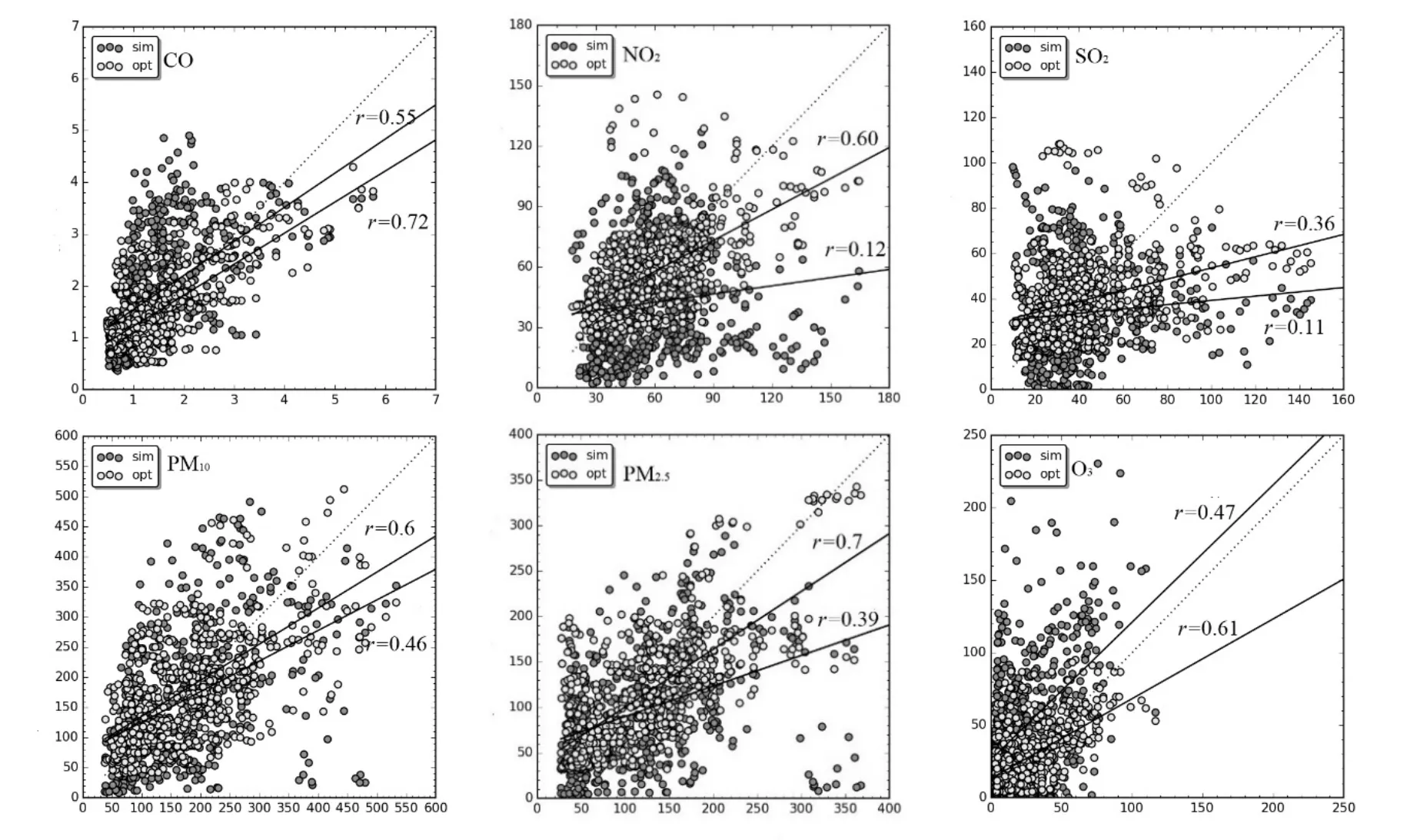
图3 2016年12月预报优化结果散点Fig.3 The result of the six pollutants optimization scatter plot in December 2016 sim为模拟值,opt为修正
散点图可以反映模拟值与观测值的线性关系,可一目了然的看出修正效果好坏程度.图 3给出了修正前后的预报值与观测值的散点分布特征,可以看出CO、O3预报值与观测值的散点多数在对角线上方,大部分预报值有一定的高估,散点分布较集中,相关系数也较高;而SO2、NO2预报值与观测值的散点多数在对角线下方,拟合线与对角线距离较远,即大多数预报值明显低于观测值,相关系数也偏低;PM2.5、PM10预报值与观测值的相关系数不低,但是其散点分布最为分散.经上述方法修正后,预报偏低或偏高现象得到很大的改善,除了SO2之外,相关系数均提高到0.6~0.7左右,且模拟值与观测值的分布较集中在对角线附近,说明修正之后预报值更接近于实际观测值.
4 结论
4.1 在源清单“Nudging”修正部分,本文结合IDW空间插值算法,以SO2、NO2、CO浓度预报值与观测值的误差迭代算子逐步修正污染源分布的方式,对模式预报值进行修正.3类污染物初始排放源的空间分布呈现大市区排放源强较大,其他各市区较小,初始源清单对CO的排放量存在一定的高估,而对SO2、NO2排放量存在一定的低估现象.从修正前后的各项指标的变化幅度来看,3类污染物中 NO2修正效果最好,其次是SO2,CO是最差.
4.2 为了改进模式在具有较大不确定性的排放源清单影响背景下,各种物理、化学过程产生的非客观性预报偏差,本文采用统计修正的方式对CMAQ模式进行后处理.用集成学习算法建立统计修正模型时,考虑到训练和预报阶段的气象条件,引入了与污染物浓度有显著相关的观测气象要素和WRF预报气象要素作为不同时间段的建模自变量.经滚动修正之后,成功消除了经“nudging”修正之后出现的反常现象,除了SO2之外,相关系数均提高到 0.6~0.7左右,优化效果颇为明显.
[1]唐孝炎,张远航,邵 敏.大气环境化学-第 2版 [M]. 北京:高等教育出版社, 2006:447-449.
[2]王占山,李晓倩,王宗爽,等.空气质量模型CMAQ的国内外研究现状 [J]. 环境科学与技术, 2013,(S1):386-391.
[3]薛文博,王金南,杨金田,等.国内外空气质量模型研究进展 [J].环境与可持续发展, 2013,38(3):14-20.
[4]Yumimoto K, Uno I. Adjoint inverse modeling of CO emissions over Eastern Asia using four-dimensional variational data assimilation [J]. Atmospheric Environment, 2006,40(35):6836-6845.
[5]孟 凯,程兴宏,徐祥德,等.基于CMAQ源同化反演方法的京津冀局地污染源动态变化特征模拟研究 [J]. 环境科学学报,2017,37(1):52-60.
[6]Xu X, Xie L, Cheng X, et al. Application of an adaptive nudging scheme in air quality forecasting in China [J]. Journal of Applied Meterology and Climatology, 2008,47(8):2105-2114.
[7]靳璐滨,臧增亮,潘晓滨,等.PM2.5和 PM2.5~10资料同化及在南京青奥会期间的应用试验 [J]. 中国环境科学, 2016,36(2):331-341.
[8]Dennis R L, Byun D W, Novak J H, et al. The next generation of integrated air quality modeling: EPA's models-3 [J]. Atmospheric Environment, 1996,30(12):1925-1938.
[9]谢 敏,钟流举,陈焕盛,等.CMAQ 模式及其修正预报在珠三角区域的应用检验 [J]. 环境科学与技术, 2012,35(2):96-101.
[10]Djalalova I, Monache L D, Wilczak J. PM2.5analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model [J]. Atmospheric Environment, 2015,119:431-442.
[11]许建明,徐祥德,刘 煜,等.CMAQ-MOS区域空气质量统计修正模型预报途径研究 [J]. 中国科学, 2005,35(z1):131-144.
[12]尤佳红,束 炯,陈亦君,等.基于MOS的杭州秋冬季空气污染预报和霾诊断 [J]. 中国环境科学, 2014,34(7):1660-1666.
[13]薛文博,许艳玲,唐晓龙,等.中国氨排放对PM2.5污染的影响 [J].中国环境科学, 2016,36(12):3531-3539.
[14]胡向军,陶健红,郑 飞,等.WRF模式物理过程参数化方案简介[J]. 甘肃科技, 2008,24(20):73-75.
[15]Hu X M, Nielsengammon J W, Zhang F. Evaluation of Three Planetary Boundary Layer Schemes in the WRF Model [J].Journal of Applied Meteorology & Climatology, 2010,49(9):1831-1844.
[16]Grell G A, Peckham S E, Schmitz R, et al. Fully coupled “online”chemistry in the WRF model [J]. Atmospheric Environment, 2005,39(37):6957-6975.
[17]王 刚.杭州市二次形成PM2.5的研究 [D]. 浙江大学, 2008.
[18]He K. Multi-resolution Emission Inventory for China (MEIC):model framework and 1990-2010 anthropogenic emissions [C]//AGU Fall Meeting, 2012.
[19]孟智勇,徐祥德,陈联寿.卫星亮温资料四维同化方案及其对“7·20”武汉特大暴雨的模拟试验 [J]. 大气科学, 2002,26(5):663-676.
[20]余小东,武 莹,何腊梅.反距离加权网格化插值算法的改进及比较 [J]. 工程地球物理学报, 2013,10(6):900-904.
[21]Chen T, Guestrin C. XGBoost: A Scalable Tree Boosting System[C]. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016:785-794.
[22]张 钰,陈 珺,王晓峰,等.Xgboost在滚动轴承故障诊断中的应用 [J]. 噪声与振动控制, 2017,37(4):166-170.
[23]Boylan J W, Russell A G. PM and light extinction model performance metrics, goals, and criteria for three-dimensional air quality models [J]. Atmospheric Environment, 2006,40(26):4946-4959.
[24]程兴宏,刁志刚,胡江凯,等.基于CMAQ模式和自适应偏最小二乘回归法的中国地区 PM2.5浓度动力-统计预报方法研究 [J].环境科学学报, 2016,36(8):2771-2782.
[25]陆维青,江峰琴,刘丽霞,等.江苏省空气质量预报与实测结果比对研究 [J]. 环境监控与预警, 2017,9(1):10-14.

