基于PMF模型的大气颗粒物多点位来源解析研究
皇甫延琦,田瑛泽*,董世豪,戴启立,史国良,周潇雨,魏 桢,千 勇,冯银厂 (南开大学环境科学与工程学院,国家环境保护城市空气颗粒物污染防治重点实验室,天津 0050;.安徽省环境监测中心站,安徽 合肥 007;.合肥市环境监测中心站,安徽 合肥 00)
随着我国经济的高速发展,环境问题日益凸显,尤其是近几年以雾霾为代表的大气颗粒物污染问题[1-5].为此 2013年国务院提出了《大气污染防治计划》十条措施.利用大气颗粒物来源解析技术,可以更精确的识别出颗粒物的主要污染源类,同时对其贡献做出定量的估算,以此更有针对性地展开与大气颗粒物有关的研究和治理工作[7].
正定矩阵因子分析模型(PMF)作为一种源未知类的受体模型在颗粒物来源解析工作中得到广泛应用.王苏蓉等[8],韩力慧等[9],陈刚等[10]利用PMF模型对我国多个大城市的大气颗粒物进行了来源解析研究.由于PMF模型主要依赖于受体数据自身变化规律进行解析,需要基于大量的受体观测数据.通常选择将单一点位的长时间序列数据纳入模型进行解析,数据量越大,模型结果越稳定[11].为了满足模型需求同时综合解析区域大气污染来源,Escrig等[12],Mooibroek等[13],Larsen等[14],Tian等[15]都尝试将多点位的受体数据合并纳入PMF模型进行计算,期望获得更加稳定且能在一定程度上反映区域颗粒物来源状况的结果.以上这些研究讨论了将多点位信息用于来源解析的意义,但是也指出将多点位合并解析会引入更多的不确定性.因此,本研究针对大气颗粒物多点位数据在不同情境下合并解析的结果进行了探讨.
本课题组之前的研究表明:将多个受体点位的数据首尾相接合并纳入 PMF模型时,点位间源成分谱差异性越小, PMF的解析结果越理想[15].基于之前的研究成果,本文在具有相同源成分谱的两个点位,研究了源贡献时间趋势(各源类的贡献在一定时间内的变化特征)和样品量对 PMF结果的影响.考虑到环境数据的复杂性和未知性,无法直接得到环境中各源类的准确贡献,因而无法对模型的拟合结果进行直接评估,所以本研究使用了模拟试验的方法,通过设定多个不同情景,对特定情景下的数据结果分别进行探讨,总结初步的规律.随后结合合肥市2014年实测PM2.5数据进行验证.最终为多点位源解析的研究提供指导和依据.
1 实验方法
1.1 正定矩阵因子分析模型
PMF(正定矩阵因子分解)模型最早于 1994年由Paatero和Tapper发表论文提出;到了1997年,Paatero进一步在论文中提出基于最小二乘法的运算方法的 PMF模型[11].随后,Paatero和Hopke又不断对PMF模型进行改进和完善,最终美国EPA官方网站对EPAPMF软件进行了推广.PMF的基本公式如下[16]:
X代表的是受体点位样品的各组分浓度矩阵;G代表源贡献矩阵;F代表源成分谱矩阵;E代表残差.对源成分谱F的各类因子进行识别,判别颗粒物污染源类,而源贡献矩阵G可以估算各颗粒物排放源对大气颗粒物的贡献情况,E可以表示在模型计算过程中的一些不确定性.
1.2 模拟数据的构建及情景设定
本文拟选择受扬尘、机动车尾气尘和硫酸盐共同影响的两个不同点位进行研究. “真实贡献值”由人为设定,污染源成分谱的构建参考了张彩艳等的研究[17],利用Matlab函数基于设定的贡献值和已构建的源谱生成一系列模拟数据.考虑了两点位的源贡献时间趋势和受体数据量大小两个因素共划分了三大类八小类情景.默认多点位数据为同步采集得到的数据,故两个点位的受体数据量同步变化.当受体数据量为50时认为数据量较少,数据量为 100及以上时认为数据量较多.具体情景分类设置如下:
(1)两点位间源贡献时间趋势完全相同
(1)- a:受体数据量较少(50条受体);(1)- b:受体数据量较多(100条受体).
(2)两点位间源贡献时间趋势完全不同
(2)- a:受体数据量较少(50条受体);(2)- b:受体数据量较多(100条受体).
(3)两点位间源贡献时间趋势部分相同
(3)- a:有两种源类的源贡献时间趋势相同,且受体数据量较少(50条受体);(3)- b:有两种源类的源贡献时间趋势相同,且受体数据量较多(100条受体);
(3)- c:两点位仅有一种源类的源贡献时间趋势相同,且受体数据量较少(50条受体);
(3)- d:两点位仅有一种源类的源贡献时间趋势相同,且受体数据量较多(100条受体).
本研究利用平均绝对误差(average absolute error, AAE)[18]来评估PMF的解析结果,AAE的计算公式如下:
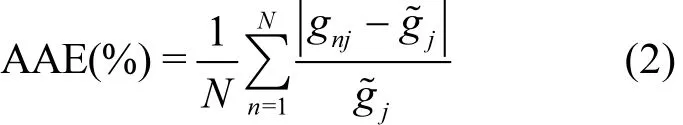
式中:1, 2, …, N表示受体的组数;gnj表示第j类源对第 n个受体的估算贡献值,µg/m3;j表示第 j类源的真实贡献值,µg/m3.
AAE值是估算贡献值与真实值的接近程度,即解析结果的准确性. AAE值越小则表示模型解析结果越准确;同时定义三种源类整体的AAE的均值为 TAAE,以此衡量模型对数据整体解析效果的稳定性,当TAAE值大于50%时可认为未能解析出稳定的结果.最终通过模型结果的稳定性和准确性来进行综合评估.
为了评价真实环境数据的点位间源贡献时间趋势,本文引入了“点位间标识组分的相关性”COR这个指标,用来判断两个点位的源贡献时间趋势关系. COR的计算公式如下:

式中:gaj和gbj表示第j类源对第a个和第b个点位的估算贡献值,µg/m3;CORREL代表Pearson相关系数,当点位间标识组分的相关性达到某一阈值(本文取 0.5),认为其标识的源类在两点位贡献的时间趋势较为一致.达到阈值的标识组分越多,说明点位间的源贡献时间趋势一致性越好.由于很难找到点位间源贡献时间趋势完全一致的数据,这里选择将单个点位的真实环境数据直接复制然后合并在一起进行解析.
1.3 合肥环境数据的采样分析
2014年夏、秋和冬季(7月23日~8月18为夏季采样,10月15日~11月2日为秋季采样,12月3日~12月16日为冬季采样)分别于合肥市庐阳区(市区北部,工业聚集区)、包河区(市区南部,行政住宅区)和瑶海区(市区东部,工业文教混合区)进行受体样品采集(如图 1所示).三个点位均使用武汉天虹公司研发的四通道采样器(型号:TH-16A,中国)对 PM2.5样品进行采集.依据滤膜特性和采样后用于化学分析的需要,本研究使用了直径47mm的聚丙烯(分析元素组分)和石英滤膜(分析碳组分和离子组分).共采集样品 252个,其中有效样品234个,有效样品约占总数93%.采样过程考虑了气象等自然因素和污染源排放等人为因素的影响.
重量分析使用电子天平(型号 CP225D,Germany).空白滤膜和采后滤膜称重前均需在恒温恒湿环境中(20 ℃ ± 1 ℃ , 5 0%±5%)平衡24h以上.碳组分分析使用光碳分析仪(DRI Model 2001,USA)对 OC(有机碳)和 EC(元素碳)进行分析.水溶性阴阳离子分析使用安徽省环境监测中心站实验室的 Dionex-ICS2000型离子色谱仪,具体分析方法可参考文献[19].无机元素分析使用美国安捷伦公司的Agilent 7700x型电感耦合等离子体质谱仪,分析测定了19种元素(Na, Mg,Al, S, K, Ca, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, As,Cd, Hg和Pb)的含量.

图1 合肥市采样点位Fig.1 Sampling sites in Hefei
2 结果和讨论
2.1 模拟实验
三种情境中三类源拟合结果的AAE值如图2所示,三种情景中PMF模型结果的TAAE值如表1所示.
2.1.1 各点位间源贡献时间趋势完全相同 情景(1)中,假设所有点位间源贡献时间趋势相同,那么合并后的多点位受体数据集可以看成是单一点位的受体数据复制了多次后合并在一起.如果将两个点位的数据看成完全一样的A数据集,那么A+A则表示两个源贡献时间趋势完全相同的受体点位的数据的集合.对于情景(1)- a,无论A或者A+A两种情形,PMF模型都无法解析出稳定合理的结果. PMF模型结果中所有源类的AAE均大于50%,且TAAE达到了约80%,甚至没有识别出合理源类结果.将两个受体点位的数据合并在一起纳入PMF模型时,解析结果有了一定改善,但仍为未得到稳定的结果.情景(1)- b中,数据集A和A+A均可以得到较好解析结果,且各源类 AAE值以及 TAAE值差异不大,机动车源AAE甚至变差.即当单个受体数据数量较多时,将多点位数据集合纳入PMF模型进行解析,解析结果不会变得更好.

图2 三种情境中各类源拟合结果的AAE值(%)Fig.2 AAE of every source contributions in three scenarios
2.1.2 各点位间源贡献时间趋势完全不同 在情景(2)中,假设两个受体点位的源贡献时间趋势情况完全不同,即模型对多点位受体数据集的解析输入数据可以看成是不同点位(A、B)的受体数据合并在了一起.在情景(2)-a中,数据集 A和 B单独解析TAAE达到了80%~90%,即PMF模型无法解析出结果,但合并后的数据集(A+B)却能够解析出较为稳定的结果,其TAAE降至约40%,同时各源类的AAE均有所降低,源解析结果稳定性和准确性均有所提高;情景(2)-b中,数据集 A和B以及合并后数据集(A+B)均能解析出稳定的结果,但不同数据集之间各源类的解析结果存在一定差异.总体来看合并后源解析结果稳定性有所提升但并非所有源类的解析结果准确性都有所提升.
2.1.3 各点位间源贡献时间趋势部分相同 在情景(3)中,假设所有点位源贡献时间趋势仅有部分是相同的.多点位受体数据集的解析的输入数据可以看成是相似点位(A、A’)的受体数据集合在了一起.情景(3)-a数据集A和A’单独解析未都能出稳定的解析结果,数据集A的所有源类解析结果均较差,各源类AAE和TAAE均大于50%;而 A’虽得到了源解析结果,但扬尘源的 AAE明显偏高达到了约 55%;合并后的数据集(A+A’)得到了较好解析结果,所有源类的AAE和TAAE均小于 35%,解析结果的稳定性和准确性有明显提高.对于情景(3)- b至情景(3)- d,数据集A、A’和(A+A’)纳入PMF模型均能解析出结果,但是其解析结果的稳定性和准确性差异较大.在情景(3)-b中,相较数据集 A 和 A’合并数据集(A+A’)的TAAE并未降低,解析出的结果的稳定性和准确性并未提高;情景(3)-c中,虽然数据集 A、A’和(A+A’)的扬尘源AAE均超过了40%,但合并后数据集(A+A’)TAAE和其他源类AAE均有所降低,解析结果的稳定性和准确性相较两个点位单独解析均有一定程度的提高.对于情景(3)-d,数据集(A+A’)TAAE 变化不大.但数据集(A+A’)机动车源和扬尘源的解析结果相较数据集A和A’却变得非常极端,机动车源的AAE下降到5%以内.而扬尘源的AAE增加至55%以上.由此看来合并后的解析结果没有明显提高,甚至对某些源类解析变差.

表1 三种情景中PMF模型结果的TAAE值Table 1 TAAE values of PMF in three scenarios
2.1.4 三种情景下拟合结果 TAAE值综合讨论 当各点位间源贡献时间趋势完全相同时,受体样品的数据量对 PMF模型解析结果影响并不大,合并解析后结果并没有变好;当各点位间源贡献时间趋势差异明显时,受体样品的数据量会对 PMF解析结果产生较大影响.当单个点位受体数据量较少时,合并解析效果的稳定性会明显提高,整体准确性会有所改善;当单个点位受体数据量较多时,合并解析可以略微提高模型的稳定性,但是各源类准确性不一定会有所升高;当各点位间源贡献时间趋势部分相同时,较少受体数据量的点位进行合并解析会增加结果的稳定性,但是不一定会提高结果的准确性.较多受体数据量的点位合并解析对结果的稳定性影响并不明显,同时部分源类解析结果的准确性可能变差.由此可见随着各点位的源贡献时间趋势差异变大,通过合并多点位受体数据进行 PMF分析,整体上有助于解析结果稳定性的提高,但是对结果准确性影响不大,甚至使部分结果变差.

表2 点位间标识组分的相关系数Table 2 CORs of tracer components between sampling sites
2.2 真实环境数据验证
考虑到真实环境数据的不确定性,使用合肥市庐阳区,包河区和瑶海区点位2014年4月~12月 PM2.5数据作进一步探究.研究期间内合肥市庐阳区,包河区的 PM2.5浓度分别为 87.4µg/m3,90.3µg/m3和 96.2µg/m3,均超过国家二级标准,污染形势较为严峻.3个点位的元素,碳组分以及水溶性离子分别占总浓度的7.4%、27.4%、54.4%,7.7%、25.9%、51.6%和8.8%、23.7%、50.3%.3个站点均体现出水溶性离子最高,碳组分其次,元素占比最低的组分分布特征.

图3 庐阳区PM2.5因子谱Fig.3 Source profiles of PM2.5 in Luyang (Hefei)
为了验证模拟实验的结论,评价不同源贡献时间趋势和不同样品量下多点位数据合并解析的适用性.将庐阳区、包河区和瑶海区三个点位数据以及其两两合并的数据集(含单点位复制然后合并的数据集)分别纳入 PMF模型进行解析,结果庐阳区单独解析以及将庐阳区和瑶海区合并解析得到了较好的结果,其他数据集未得到合理结果.对于庐阳区的解析结果共提取出四个因子.因子谱如图3所示,因子1中主要包含OC、EC、NO3-,这指示了机动车源;因子 2主要包含SO42-、NO3-、NH4+、OC 等,这指示了二次源;因子 3主要包含 OC、EC、SO42-、NO3-、Al、Si,这指示了燃煤源;因子 4主要包含 SO42-、OC、EC、Al、Si、Ca等,这指示了城市扬尘源.其中,二次源和燃煤源对合肥市的贡献较高分别占到了 40.9%和 27.1%,其次是城市扬尘源和机动车源分别占到了 19.4%和 11.5%.对于庐阳区和瑶海区合并解析也提取了四个因子(图4).依据标识组分分析可以看出因子1为机动车源,因子2是二次源,因子 3是燃煤源,因子 4是城市扬尘源,其贡献分别为 16.9%,40.1%,29.7%,11.4%. 这与陈刚等[11]关于合肥城区 PM2.5季节污染特征及来源解析研究中的结果较为一致.

图4 庐阳区&瑶海区PM2.5因子谱Fig.4 Source profiles of PM2.5 in Luyang & Yaohai(Hefei)
结合点位间标识组分的相关性(表2),可以看出庐阳区和瑶海区仅有 SO42-的相关性较好,其整体源类贡献时间趋势差异性最大,最终合并解析得到较好的结果.与模拟实验的结论基本吻合,即随着各点位的源贡献时间趋势差异变大,通过合并多点位受体数据进行PMF分析,整体上有助于解析结果稳定性的提高.此外,可能由于不同点位真实环境数据的差异,仅庐阳区单点位直接解析得到了较好结果.因此选择将多点位数据合并纳入PMF模型进行解析需要注意使用的前提条件,只有当多个点位受相同源类影响,且点位间源贡献时间趋势存在较大差异时,合并解析可以得到较好的结果.
3 结论
3.1 在各点位间源贡献时间趋势完全一致时,无论环境信息是否充足,通过合并不同点位的受体数据来增加输入数据的数量都不会令PMF模型的解析准确性有明显提高.
3.2 当各点位间源贡献时间趋势差异明显时,将不同点位数据合并解析可以提高模型结果的稳定性,但是不一定会提高结果的准确性.
3.3 当各点位间源贡献时间趋势部分相同时,虽然解析结果的稳定性有所上升,但是结果的准确性不一定变好,甚至变差.
3.4 选择将多点位数据合并纳入 PMF模型进行解析需要注意使用的前提条件,只有当多个点位受相同源类影响,且点位间源贡献时间趋势存在较大差异时,合并解析可以得到较好的结果.
[1]胡 敏,唐 倩,彭剑飞,等.我国大气颗粒物来源及特征分析[J]. 环境与可持续发展, 2011,36(5):15-19.
[2]Chan C K, Yao X H. Air pollution in mega cities in China [J].Atmospheric Environment, 2008,42:1-42.
[3]Zhang Y H, Hu M, Zhong L J, etl. Regional Integrated Experiments on Air Quality over Pearl River Delta 2004 (PRIDEPRD2004): Overview [J]. Atmospheric Environment 2008,42(25):6157-6173.
[4]Laupsa H, Denby B, Larssen S, et al. Source apportionment of particulate matter (PM2.5) in an urban area using dispersion,receptor and inverse modeling [J]. Atmospheric Environment 2009,43:4733-4744.
[5]Chen D S, Cheng S Y, Liu L, et al. An integrated MM5—CMAQ modeling approach for assessing trans-boundary PM10contribution to the host city of 2008 Olympic summer games—Beijing, China [J]. Atmospheric Environment, 2007,41:1237-1250.
[6]《大气污染防治行动计划》[EB/OL]. (2014-09-13) http://www.gov.cn/ zwgk/2013-09/12/content_2486773.htm.
[7]朱 坦.大气颗粒物来源解析 [M]. 北京:科学出版社, 2012.
[8]王苏蓉,喻义勇,王勤耕,等.基于PMF模式的南京市大气细颗粒物源解析 [J]. 中国环境科学, 2015,35(12):3535-3542.
[9]韩力慧,张 鹏,张海亮,等.北京市大气细颗粒物污染与来源解析研究 [J]. 中国环境科学, 2016,36(11):3203-3210.
[10]陈 刚,刘佳媛,皇甫延琦,等.合肥城区 PM10及 PM2.5季节污染特征及来源解析 [J]. 中国环境科学, 2016,36(7):1938-1946.
[11]Paatero P. Least squares formulation of robust non-negative factor analysis [J]. Chemometrics and Intelligent Laboratory Systems 1997,37:23-35.
[12]Escrig A, Monfort E, Celades I, et al. Application of optimally scaled target factor analysis for assessing source contribution of ambient PM10[J]. J. Air & Waste Manage, 2009,59:1296—1307.
[13]Mooibroek D, Schaap M, Weijers E P, et al. Source apportionment and spatial variability of PM2.5using measurements at five sites in the Netherlands [J]. Atmospheric Environment, 2011,45(25):4180-4191.
[14]Larsen B R, Gilardoni S, Stenström K, et al. Sources for PM air pollution in the Po Plain, Italy: II. Probabilistic uncertainty characterization and sensitivity analysis of secondary and primary sources [J]. Atmospheric Environment, 2012,50:203-213.
[15]Tian Y Z, Shi G L, Han B, et al. The accuracy of two- and three-way positive matrix factorization models: Applying simulated multisite data sets [J]. Journal of the Air & Waste Management Association, 2014,64(10):1122-1129.
[16]Hopke PK. Recent developments in receptor modeling [J].Journal of chemometrics, 2003,17:255-265.
[17]张彩艳,吴建会,张 普,等.成都市冬季大气颗粒物组成特征及来源变化趋势 [J]. 环境科学研究, 2014,27(7):782-789.
[18]Javitz H S, Watson J G, Robinson N. Performance of the chemical mass balance model with simulated local-scale aerosol [J].Atmospheric Environment, 1988,22:2309—2322.
[19]Zhang T, Cao J J, Tie X X, et al. Water-soluble ions in atmospheric aerosols measured in Xi'an, China: Seasonal variations and sources [J]. Atmospheric Research, 2011,102(1):110-119.

