叉车电液伸缩臂的控制算法研究

石璐奇，唐廷彩，高 强，陈 硕，莫浩彬，王泽灏

（南京农业大学工学院，江苏南京210031）

伸缩臂叉车在传统叉车的基础上，结合了汽车起重机的伸缩臂结构，实现了对大型物品的远距离运输、堆垛。

电液比例控制技术借助电液比例阀实现了电液控制，有利于液压系统朝智能化的方向发展[1-2]。PID控制是一种经典的控制方法。它通过对控制参数的比例、积分、微分运算来调整控制参数，进行控制[3]。但PID控制不能进行参数自适应调整，所以增加了模糊控制，应用模糊PID在Matlab的Simulink中搭建模型，对伸缩臂电液控制系统的工作特性进行仿真分析。

1 叉车电液伸缩臂系统原理

叉车电液伸缩臂液压系统是一种基于电液比例控制技术的液压系统。该液压系统主要包括伸缩回路、变幅回路和辅助回路。三个回路由同一个液压泵供油，原理相同，使用了相同的液压元件。液压系统原理如图1所示。当控制器向三位四通换向阀输入信号时，控制三位四通换向阀的左通和右通。换向阀右通，液压油缸左侧进油，活塞向左运动；换向阀左通，液压油缸右侧进油，活塞向右运动。油缸活塞杆带动伸缩臂的工作，调整伸缩臂的长度和高度。当控制器不输入信号时，油液经换向阀流回油箱。

图1 叉车电液伸缩臂液压系统原理图

2 模糊PID模型

选择使用二维模糊控制器作为模糊PID控制器。模糊控制器的输入变量为牵引力偏差E和偏差变化率EC，输出变量为参数修正量KP、KI、KD.

2.1 输入输出变量论域及模糊子集确定

所研究的系统变量为连续变量，但模糊控制器只能接收离散数据，所以将论域离散化[4]。误差E、误差变化率EC和输出变量KP、KI、KD三个变量的基本域为它们的取值范围，且都为精确量。将E、EC、KP、KI和KD的基础域分成离散若干级，得出5个量的语言子集域。

取误差E模糊集合域为：E={-n，-n+1，…，0，…，n-1，n}

取误差变化率EC的模糊集合域为：EC={-m，-m+1，…，0，…，m-1，m}

取输出变量KP的模糊集合域为：

KP={-i，-i+1，…，0，…，i-1，i}

取输出变量KI的模糊集合域为：

KI={-l，-l+1，…，0，…，l-1，l}

取输出变量KD的模糊集合域为：

KD={-s，-s+1，…，0，…，s-1，s}

首先将误差E、误差变化率EC、输出变量KP、KI、KD 改变分为“高”、“中”、“低”3 个级别加以区别。又因为误差E、误差变化率EC、输出变量KP、KI、KD可为正值或负值。依据模糊PID控制器的控制规律以及经典PID的控制方法[5]，本文将语言论域分为7个模糊子集，语言变量值记为：“正高”（PH）、“正中”（PM）、“正低”（PL）“零”（Z）、“负低”（NL）、“负中”（NM）、“负高”（NH），7 个档次。

为使子集能更好的包含研究区间，以免出现不受控的情况，可取 n，m，i，l，s均为 3.虽然 n，m，i，l，s选取数值愈大，精准度愈准，但会加大计算的工作量，导致系统响应变缓。

为使计算方便，引入量化因子K.

当基础研究范围的数值化级数选定后，K的大小就反应了基本论域的大小变化趋势。当K变大时，会使基础研究范围变小，反之，当K变小时，会使基础研究范围变大，从而引起偏差调控的反应敏捷度的下降。

模糊控制器根据控制规则，推理出输出变量后，不能直接作用，必须将其化为输出变量基础范围中的对应值才可以使用，所以引入比例因子Ku.

当控制变量论域的最大值是定量时，比例因子Ku与基础研究范围的量化级数成反比，若Ku取值太大，会引起调控过程阻尼程度的降低。Ku选值过小，被控系统反应变缓。

下图2是本研究所选取的隶属度函数图像，用来确定输入输出变量的隶属度关系。

图 2 D、DE、KP、KI、KD 隶属度函数图像

2.2 模糊控制规则

模糊集合域D、DE输入至模糊推理器，结合控制规则，推理合成输出变量KP、KI、KD，对PID参数进行修正，最后输出控制信号，对系统产生作用。模糊控制规则通常基于工作人员与研究人员经验总结得出，以“if……then……”的形式来表示。本次实验的模糊控制器使用双输入三输出控制。

2.3 叉车电液伸缩臂系统模糊PID自适应控制仿真

首先利用Matlab的模糊推理工具箱fuzzy建立模糊推理系统。再根据隶属度关系，进行输入输出变量隶属度关系的设置。在规则编辑器中按照模糊控制状态表的内容输入控制规则。在Matlab/Simulink中建立模糊PID模型。

Simulink中搭建的PID模型如图3所示。

图3 叉车电液伸缩臂系统的仿真模型

图4 模糊PID自适应控制器模型

Simulink中搭建的模糊PID模型如图4所示。

3 运行与分析

3.1 高度为定值

设定目标高度为0.6 m，仿真时间设置为5 s，仿真结果如图5所示。

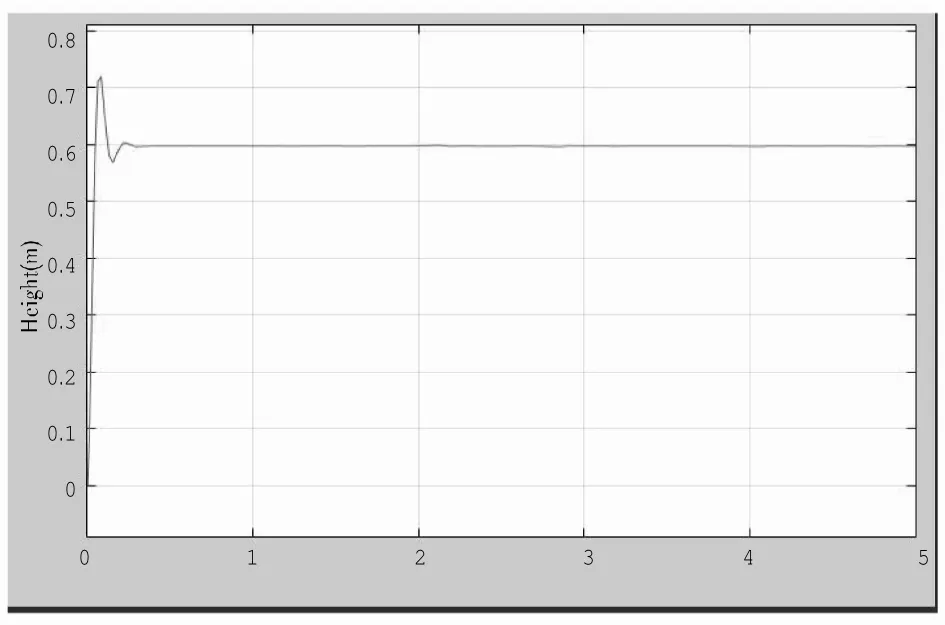
图5 PID仿真结果图

通过上图可知，高度为0.6 m时，仿真初期有极短时间的震荡，高度达到稳定时间为0.2 s左右，之后稳定在0.6 m，满足系统的高度要求。

3.2 高度改变

在工作进行时，根据工作要求，改变高度。设定20 s时，由0.3 m改为0.6 m，仿真时间设为50 s，PID以及模糊PID仿真结果如图6所示（其中，位于上方的曲线为PID仿真结果图，位于下方的曲线为模糊PID仿真结果图）。

图6 PID和模糊PID仿真结果图

由图6可知，PID仿真在20 s时高度出现阶跃变化，系统响应时间大约为10 s，有较大的震荡现象，所以PID模型满足工作要求，同时还可以进行进一步改善。而模糊PID仿真初期响应时间缩短为5 s左右，20 s时高度变化系统响应时间为5 s左右，同时震荡现象明显减小。

4 结束语

在模糊PID控制算法控制下的叉车电液举升系统具有响应迅速，货叉举升速度平稳的优点，这对提高叉车的精细化操作有重要意义。

根据对叉车电液伸缩臂控制算法的研究，分别设计了PID控制器和模糊PID控制器，通过建立叉车电液伸缩臂控制系统模型进行系统性能分析。试验结果表明，在采用模糊PID控制方法之后，电液伸缩臂系统控制的过程更加平稳，响应速度更快，作业效率更高。

[1]汪 亮.单缸插销电液控制系统仿真分析研究[D].大连：大连理工大学，2015.

[2]励 伟.大流量2D电液比例换向阀的设计及研究[D]杭州：浙江工业大学，2013.

[3]林 浩.模糊PID控制器仿真研究[D].贵阳：贵州大学，2005.

[4]李明生，赵建军，朱忠祥，等.拖拉机电液悬挂系统模糊PID自适应控制方法[J].农业机械学报，2013（10）:295-300.

[5]赵永娟，孙华东.基于Matlab的模糊PID控制器的设计和仿真[D].太原：中北大学，2005.